【数据结构】八大排序
目录
1. 排序的概念及其作用
1.1 排序的概念
1.2 排序运用
1.3 常见的排序算法
2. 常见排序算法的实现
2.1 插入排序
2.1.1 基本思想
2.1.2 直接插入排序
2.1.3 希尔排序(缩小增量排序)
2.2 选择排序
2.2.1 基本思想
2.2.2 直接选择排序
2.2.3 堆排序
2.3 交换排序
2.3.1 基本思想
2.3.2 冒泡排序
2.3.3 快速排序
2.3.3.1 快速排序优化
2.3.3.2 快速排序非递归
2.4 归并排序
2.5 非比较排序
3. 排序算法复杂度及稳定性分析
1. 排序的概念及其作用
1.1 排序的概念
排序:所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。
稳定性:假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,r [ i ] = r [ j ],且 r [ i ] 在 r [ j ] 之前,而在排序后的序列中,r [ i ] 仍在 r [ j ] 之前,则称这种排序算法是稳定的;否则称为不稳定的。
内部排序:数据元素全部放在内存中的排序。
外部排序:数据元素太多不能同时放在内存中,根据排序过程的要求不能在内外存之间移动数据的排序。
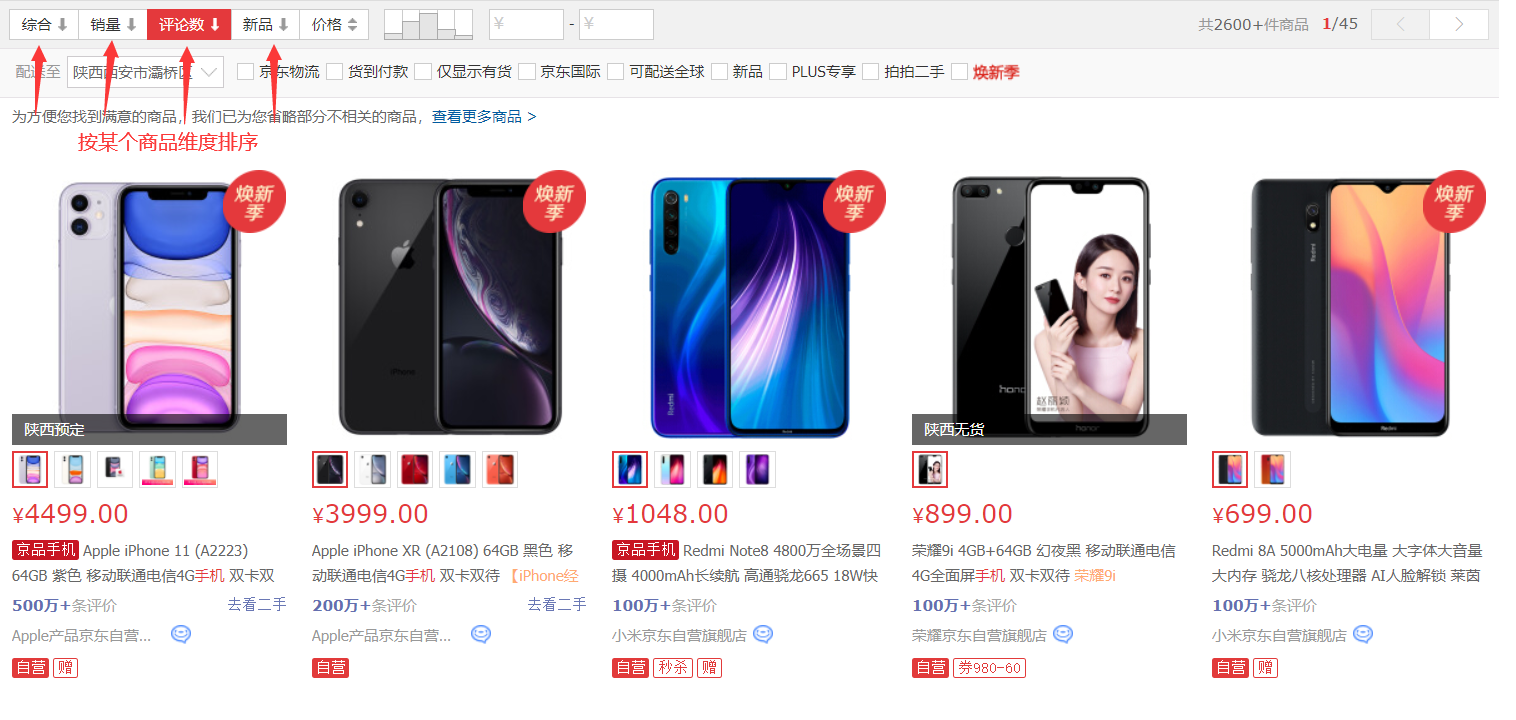
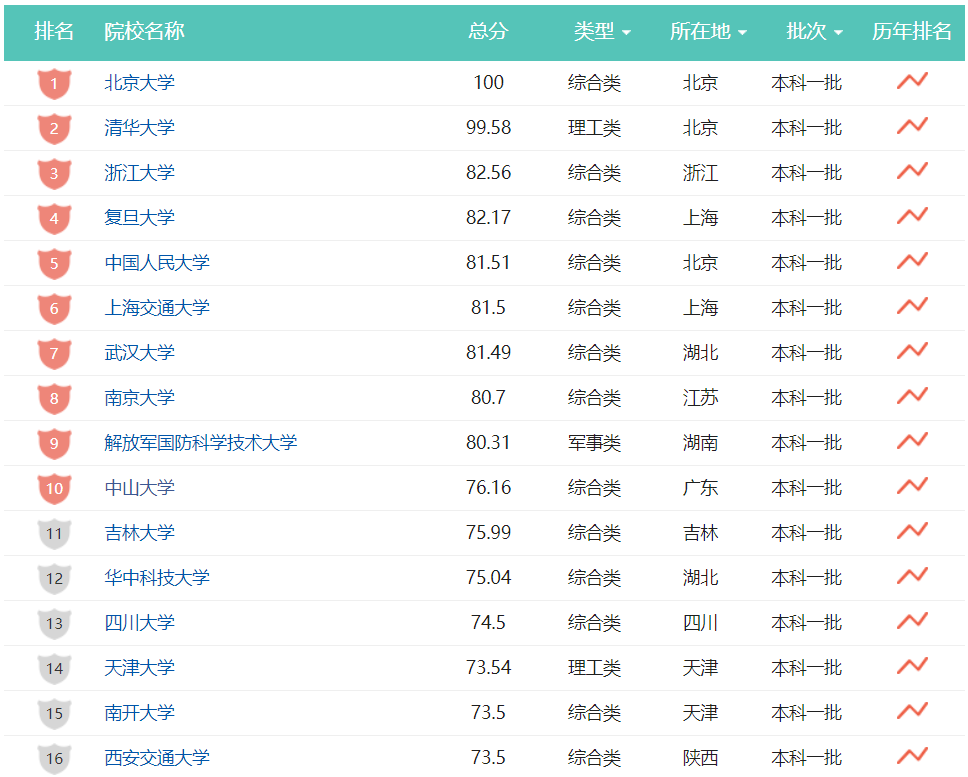
1.2 排序运用
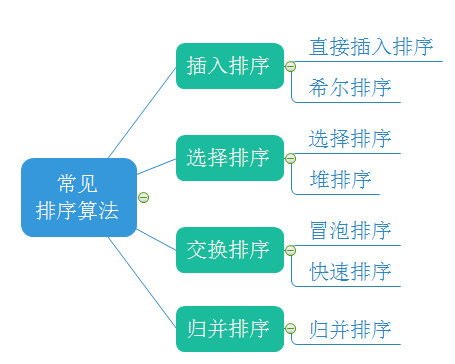
1.3 常见的排序算法
// 排序实现的接口// 插入排序
void InsertSort(int* a, int n);// 希尔排序
void ShellSort(int* a, int n);// 冒泡排序
void BubbleSort(int* a, int n);// 堆排序
void HeapSort(int* a, int n);// 选择排序
void SelectSort(int* a, int n);// 快速排序 递归实现
void QuickSort(int* a, int begin, int end);
// 快速排序 非递归实现
void QuickSortNonR(int* a, int begin, int end);// 归并排序 递归实现
void MergeSort(int* a, int n);
// 归并排序 非递归实现
void MergeSortNonR(int* a, int n);// 计数排序
void CountSort(int* a, int n);2. 常见排序算法的实现
2.1 插入排序
2.1.1 基本思想
直接插入排序是一种简单的插入排序法,其基本思想是:
把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中,直到所有的记录插入完为止,得到一个新的有序序列 。
实际中我们玩扑克牌时,就用了插入排序的思想

2.1.2 直接插入排序
当插入第 i(i >= 1)个元素时,前面的 array[0],array[1],…,array[i-1] 已经排好序,此时用 array[i] 的排序码与 array[i-1],array[i-2], … 的排序码顺序进行比较,找到插入位置即将 array[i] 插入,原来位置上的元素顺序后移。
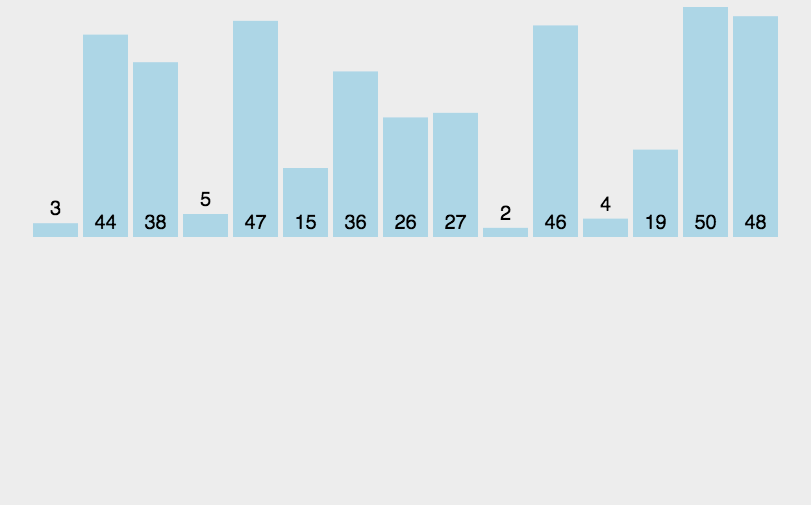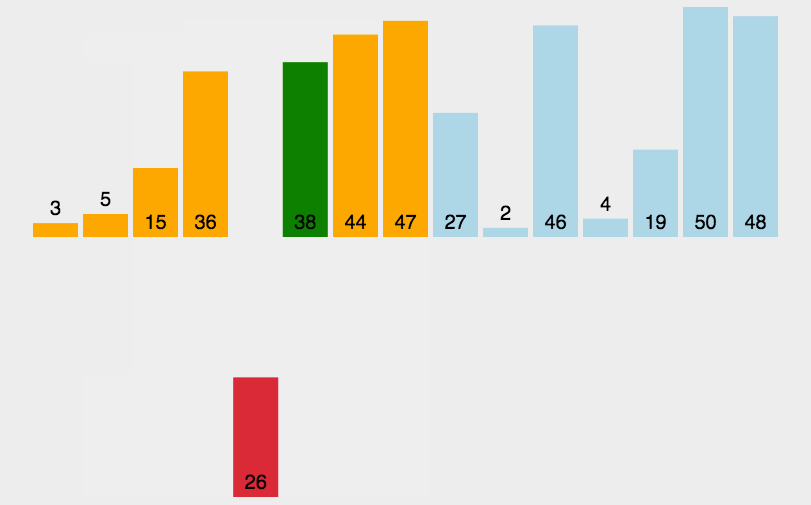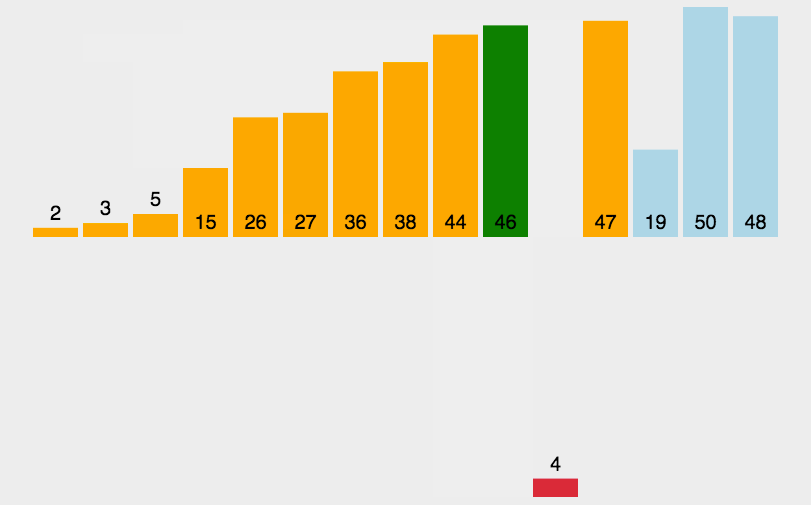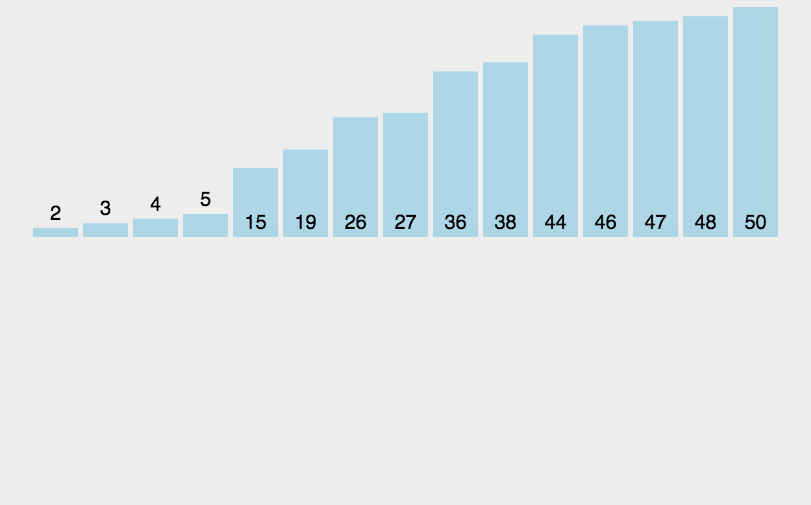
// 直接插入排序
void InsertSort(int* a, int n)
{for (int i = 0; i < n - 1; i++){int end = i;int tmp = a[end + 1];while (end >= 0){if (tmp < a[end]){a[end + 1] = a[end];}else{break;}--end;}a[end + 1] = tmp;}
}直接插入排序的特性总结:
- 元素集合越接近有序,直接插入排序算法的时间效率越高
- 时间复杂度:O(N^2)
- 空间复杂度:O(1),它是一种稳定的排序算法
- 稳定性:稳定
2.1.3 希尔排序(缩小增量排序)
希尔排序(Shell Sort)是插入排序的一种。也称缩小增量排序,是直接插入排序算法的一种更高效的改进版本。希尔排序是非稳定排序算法。该方法因DL.Shell于1959年提出而得名。希尔排序是记录按下标的一定增量分组,对每组使用直接插入排序算法排序;随着增量逐渐减少,每组包含的关键词越来越多,当增量减至1时,整个文件恰被分成一组,算法便终止。
我们分割待排序记录的目的是减少待排序记录的个数,并使整个序列向基本有序发展。而如上面这样分完组后,就各自排序的方法达不到我们的要求。因此,我们需要采取跳跃分割的策略;将相距某个“增量”的记录组成一个子序列,这样才能保证在子序列内分别进行直接插入排序后得到的结果是基本有序而不是局部有序。
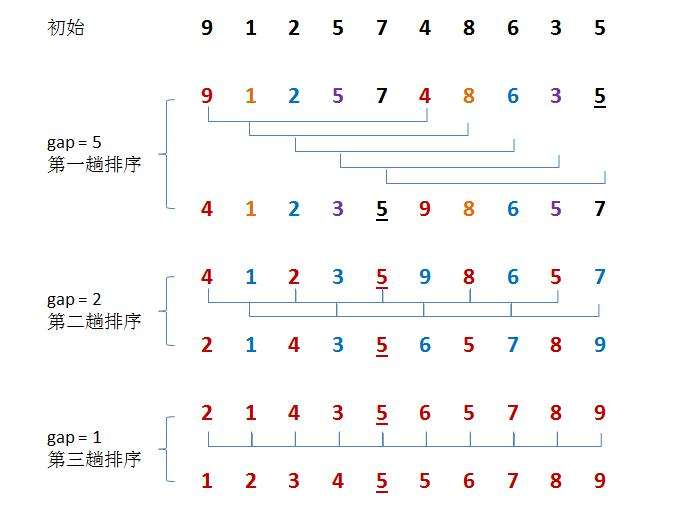
// 希尔排序
void ShellSort(int* a, int n)
{int gap = n;while (gap > 1){gap = gap / 3 + 1;for (int i = 0; i < n - gap; i++){int end = i;int tmp = a[end + gap];while (end >= 0){if (tmp < a[end]){a[end + gap] = a[end];end -= gap;}else{break;}}a[end + gap] = tmp;}}
}希尔排序的特性总结:
1. 希尔排序是对直接插入排序的优化。
2. 当 gap > 1 时都是预排序,目的是让数组更接近于有序。当 gap == 1 时,数组已经接近有序的了,这样就会很快。这样整体而言,可以达到优化的效果。我们实现后可以进行性能测试的对比。
3. 希尔排序的时间复杂度不好计算,因为 gap 的取值方法很多,导致很难去计算,因此在好些树中给出的希尔排序的时间复杂度都不固定:
《数据结构(C语言版)》--- 严蔚敏
《数据结构-用面相对象方法与C++描述》--- 殷人昆
因为咋们的gap是按照Knuth提出的方式取值的,而且Knuth进行了大量的试验统计,我们暂时就按照:
到
来算。
4. 稳定性:不稳定
2.2 选择排序
2.2.1 基本思想
每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到全部待排序的数据元素排完 。
2.2.2 直接选择排序
- 在元素集合 array[ i ] -- array[ n-1 ] 中选择关键码最大(小)的数据元素
- 若它不是这组元素中的最后一个(第一个)元素,则将它与这组元素中的最后一个(第一个)元素交换
- 在剩余的 array[ i ] -- array[ n-2 ](array[ i+1 ] -- array[ n-1 ])集合中,重复上述步骤,直到集合剩余1个元素
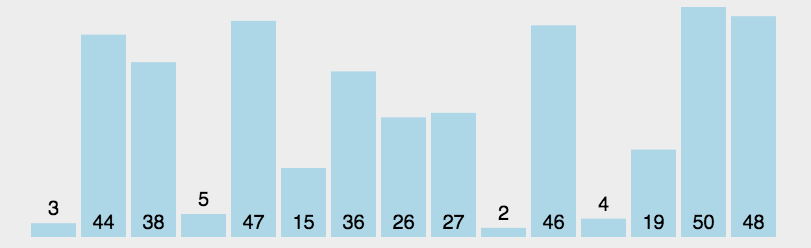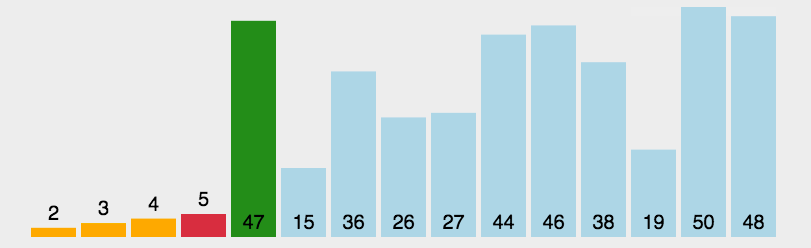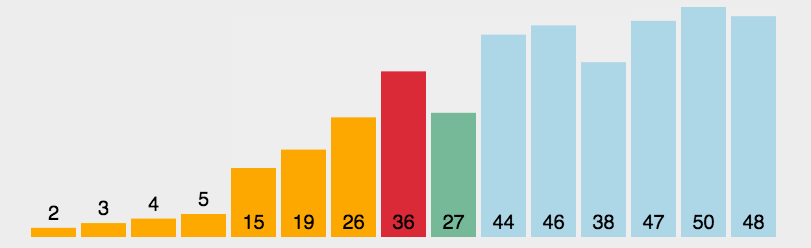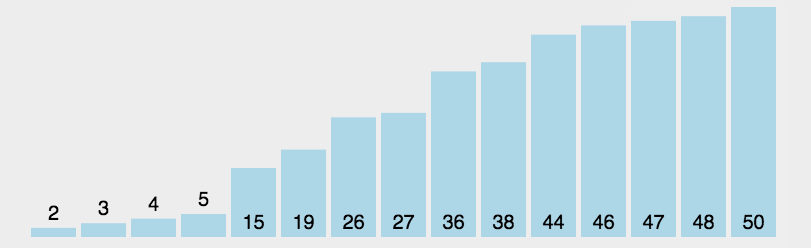
// 直接选择排序
void SelectSort(int* a, int n)
{int begin = 0, end = n - 1;while (begin < end){int mini = begin, maxi = begin;for (int i = begin + 1; i <= end; i++){if (a[i] > a[maxi]){maxi = i;}if (a[i] < a[mini]){mini = i;}}Swap(&a[begin], &a[mini]);// max如果被换走了,修正一下if (maxi == begin){maxi = mini;}Swap(&a[end], &a[maxi]);++begin;--end;}
}直接选择排序的特性总结:
- 直接选择排序思考非常好理解,但是效率不是很好。实际中很少使用
- 时间复杂度:O(N^2)
- 空间复杂度:O(1)
- 稳定性:不稳定
2.2.3 堆排序
堆排序(Heapsort)是指利用堆积树(堆)这种数据结构所设计的一种排序算法,它是选择排序的一种。它是通过堆来进行选择数据。需要注意的是排升序要建大堆,排降序建小堆。
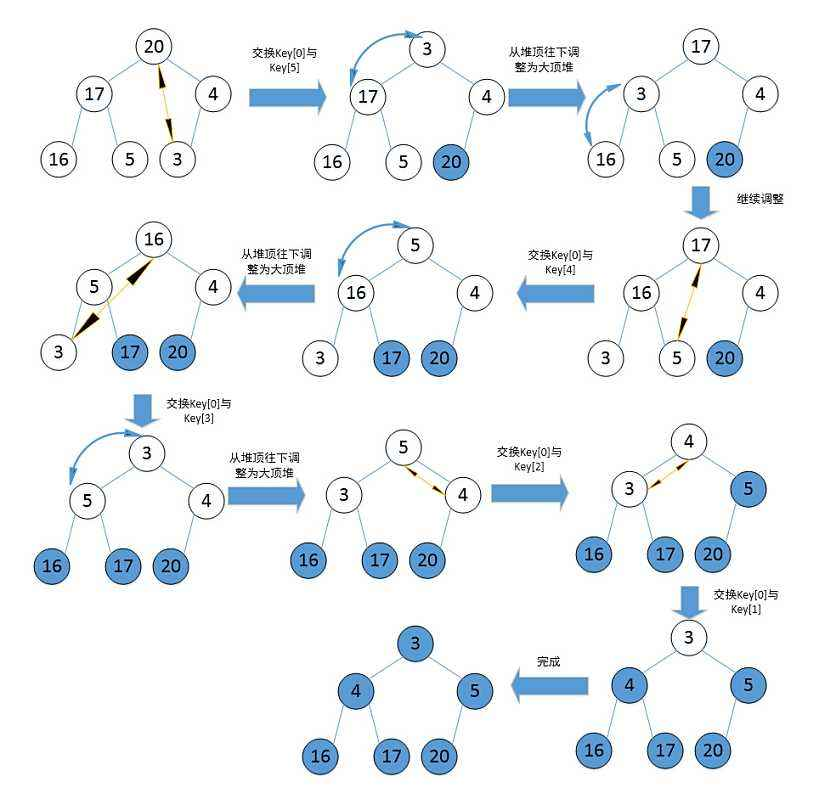
// 向下调整
void AdjustDown(int* a, int n, int parent)
{int child = parent * 2 + 1;while (child < n){// 找出小的那个孩子if (child + 1 < n && a[child + 1] > a[child]){++child;}if (a[child] > a[parent]){Swap(&a[child], &a[parent]);// 继续往下调整parent = child;child = parent * 2 + 1;}else{break;}}
}// 堆排序
void HeapSort(int* a, int n)
{// 向下调整建堆for (int i = (n - 1 - 1) / 2; i >= 0; i--){AdjustDown(a, n, i);}int end = n - 1;while (end > 0){Swap(&a[0], &a[end]);AdjustDown(a, end, 0);--end;}
}堆排序的特性总结:
- 堆排序使用堆来选数,效率就高了很多。
- 时间复杂度:O(N*logN)
- 空间复杂度:O(1)
- 稳定性:不稳定
2.3 交换排序
2.3.1 基本思想
所谓交换,就是根据序列中两个记录键值的比较结果来对换这两个记录在序列中的位置,交换排序的特点是:将键值较大的记录向序列的尾部移动,键值较小的记录向序列的前部移动。
2.3.2 冒泡排序
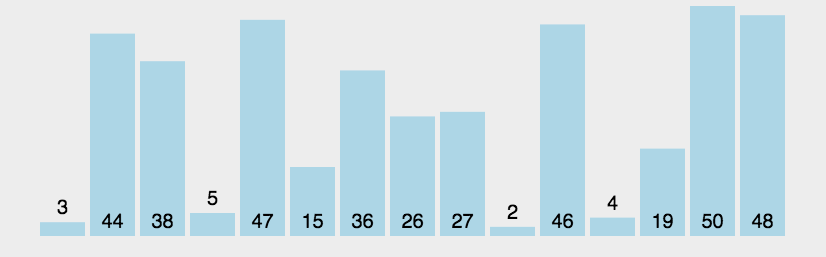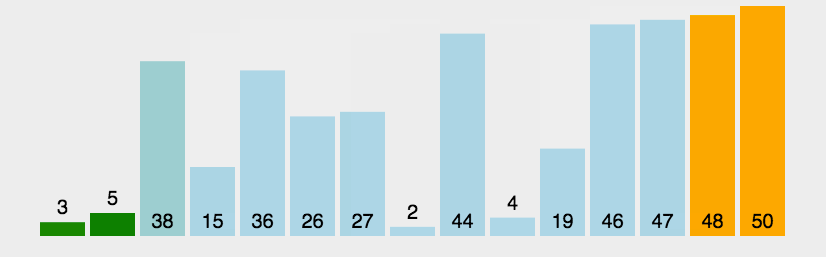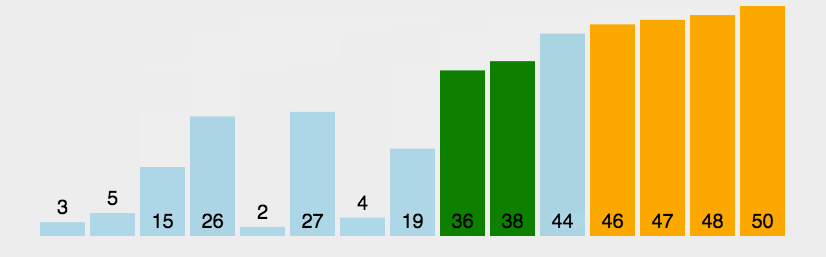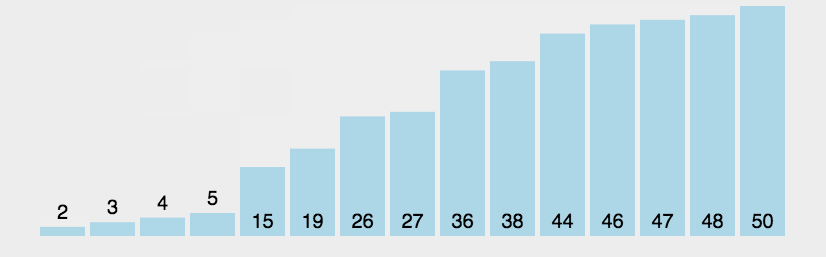
// 冒泡排序
void BubbleSort(int* a, int n)
{for (int j = 0; j < n; j++){int exchange = 0;for (int i = 1; i < n - j; i++){if (a[i - 1] > a[i]){Swap(&a[i - 1], &a[i]);exchange = 1;}}if (exchange == 0)break;}
}冒泡排序的特性总结:
- 冒泡排序是一种非常容易理解的排序
- 时间复杂度:O(N^2)
- 空间复杂度:O(1)
- 稳定性:稳定
2.3.3 快速排序
快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法,其基本思想为:任取待排序元素序列中的某元素作为基准值,按照该排序码将待排序集合分割成两子序列,左子序列中所有元素均小于基准值,右子序列中所有元素均大于基准值,然后最左右子序列重复该过程,直到所有元素都排列在相应位置上为止。
// 假设按照升序对a数组中[begin, end]区间中的元素进行排序
void QuickSort(int* a, int begin, int end)
{if (begin >= end)return;// 按照基准值对a数组的[begin, end]区间中的元素进行划分int keyi = PartSort1(a, begin, end);// 划分成功后以keyi为边界形成了左右两部分[begin, keyi-1]和[keyi+1, end]// 递归排[begin, keyi-1]QuickSort(a, begin, keyi - 1);// 递归排[keyi+1, end]QuickSort(a, keyi + 1, end);
}上述为快速排序递归实现的主框架,发现与二叉树前序遍历规则非常像,大家在写递归框架时可想想二叉树前序遍历规则即可快速写出来,后序只需分析如何按照基准值来对区间中数据进行划分的方式即可。
将区间按照基准值划分为左右两半部分的常见方式有:
1. hoare版本
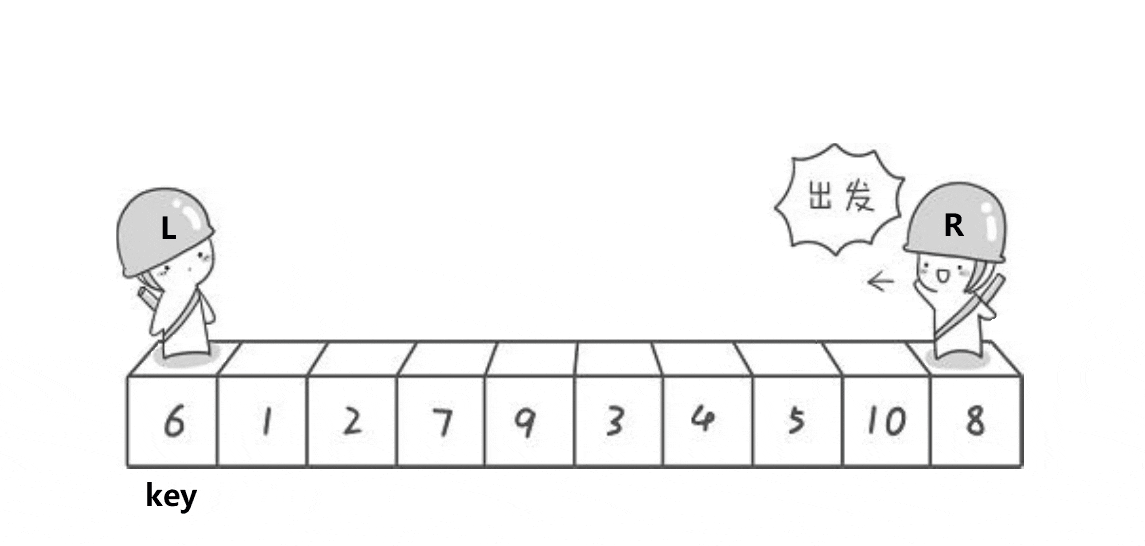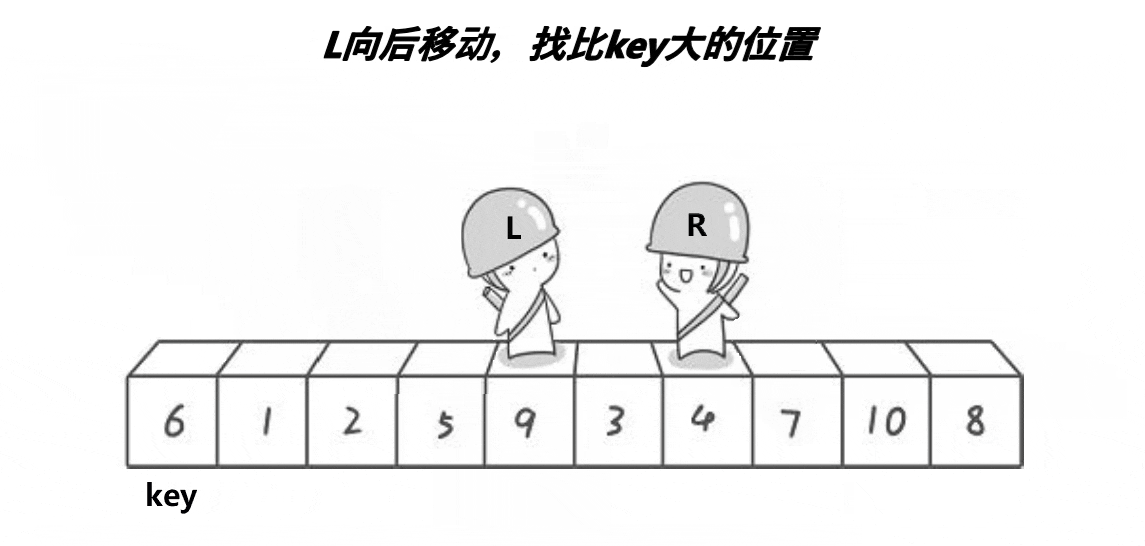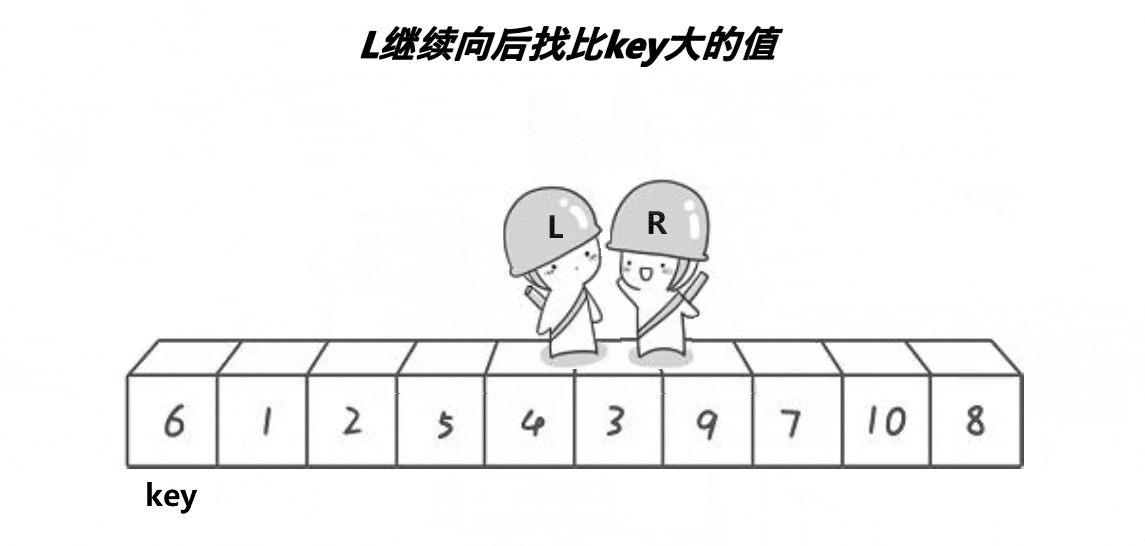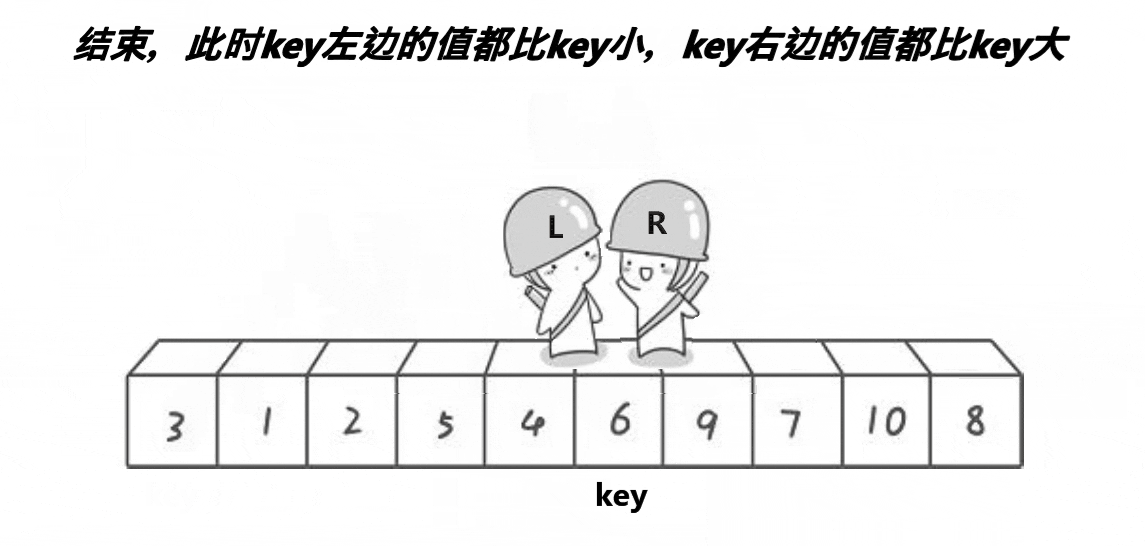
// 快速排序Hoare版本
int PartSort1(int* a, int left, int right)
{// 三数取中优化,下面会讲int midi = GetMidi(a, left, right);Swap(&a[left], &a[midi]);int keyi = left;while (left < right){// 找小while (left < right && a[right] >= a[keyi]){--right;}// 找大while (left < right && a[left] <= a[keyi]){++left;}Swap(&a[left], &a[right]);}Swap(&a[keyi], &a[left]);return left;
}2. 挖坑法
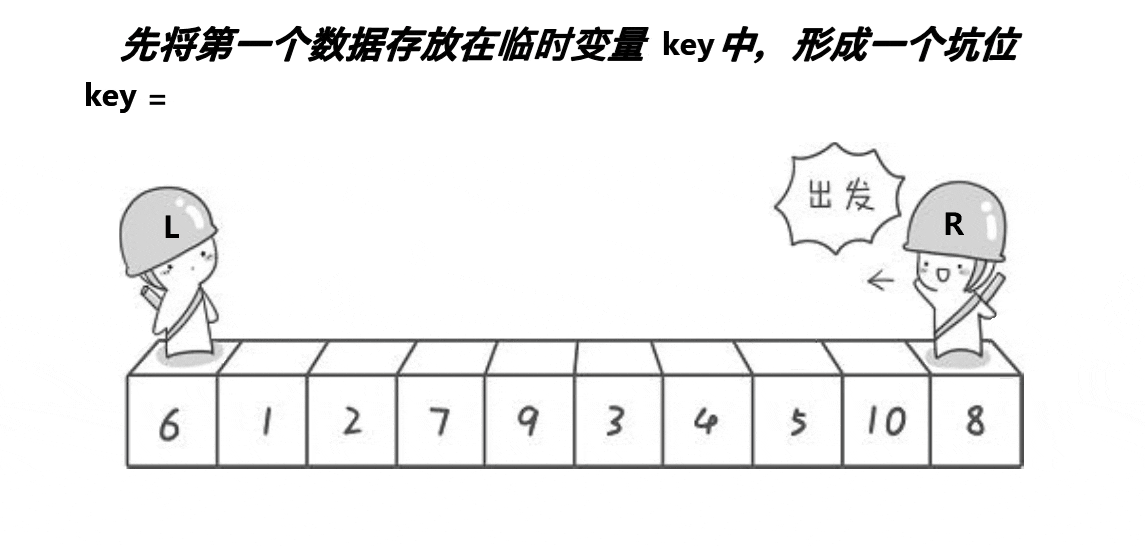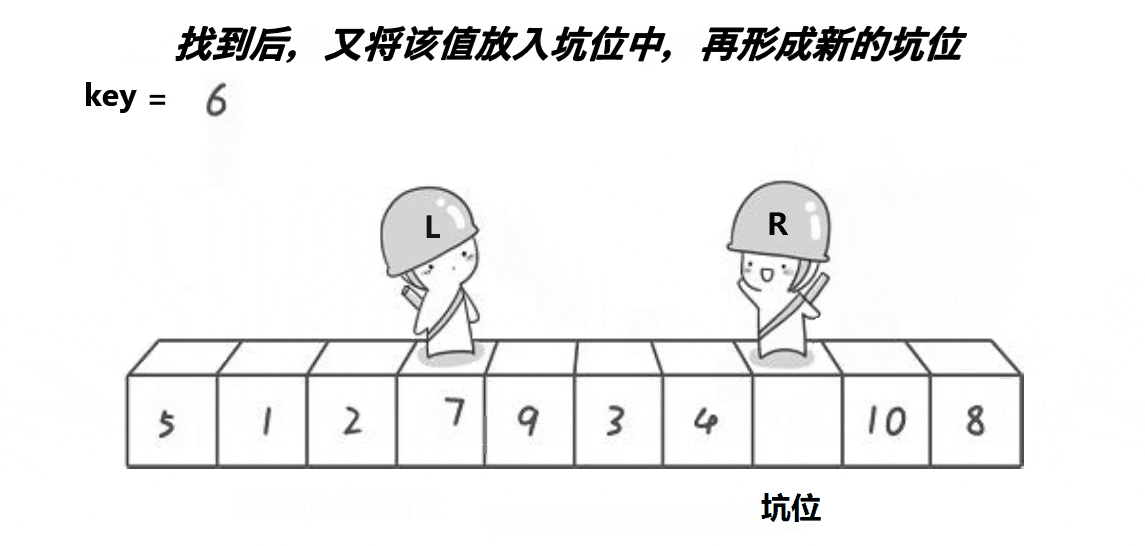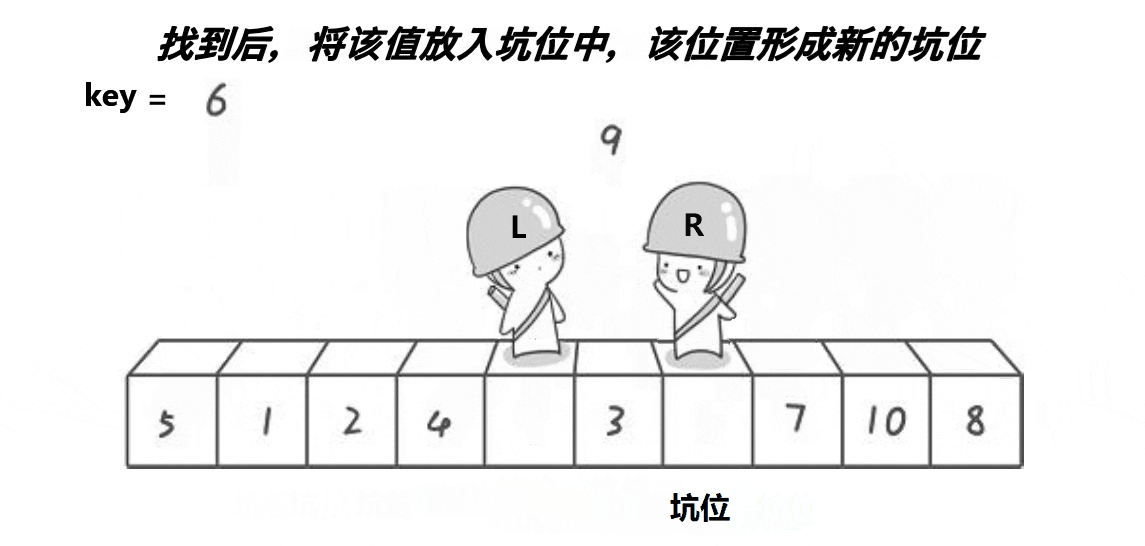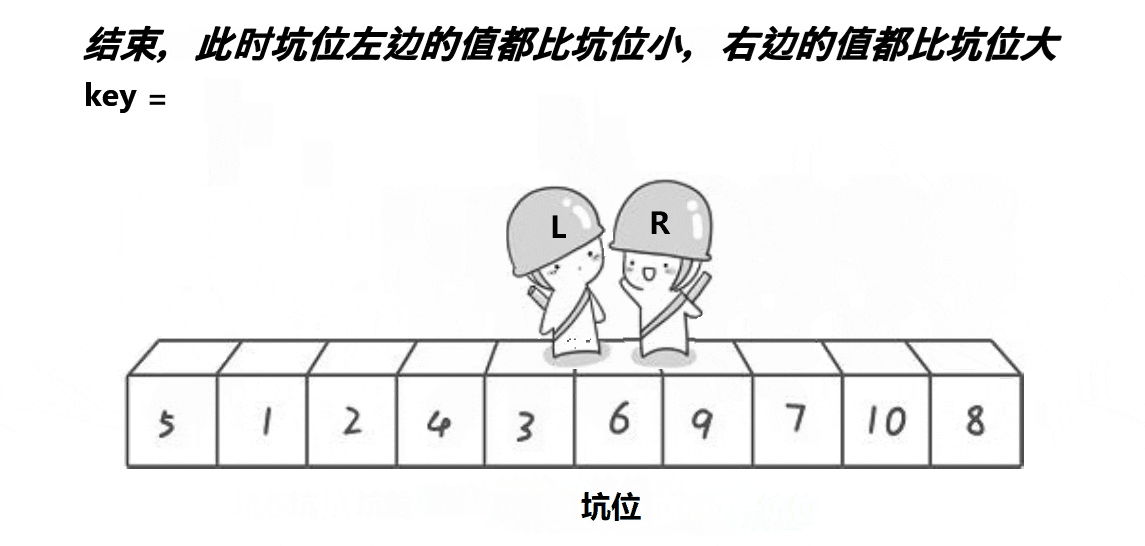
// 快速排序挖坑法
int PartSort2(int* a, int left, int right)
{int midi = GetMidi(a, left, right);Swap(&a[left], &a[midi]);int key = a[left];// 保存key的值后,左边形成第一个坑int hole = left;while (left < right){// 右边先走,找小,填到左边的坑,右边形成新的坑位while (left < right && a[right] >= key){--right;}a[hole] = a[right];hole = right;// 左边再走,找大,填到右边的坑,左边形成新的坑位while (left < right && a[left] <= key){++left;}a[hole] = a[left];hole = left;}a[hole] = key;return hole;
}3. 前后指针版本
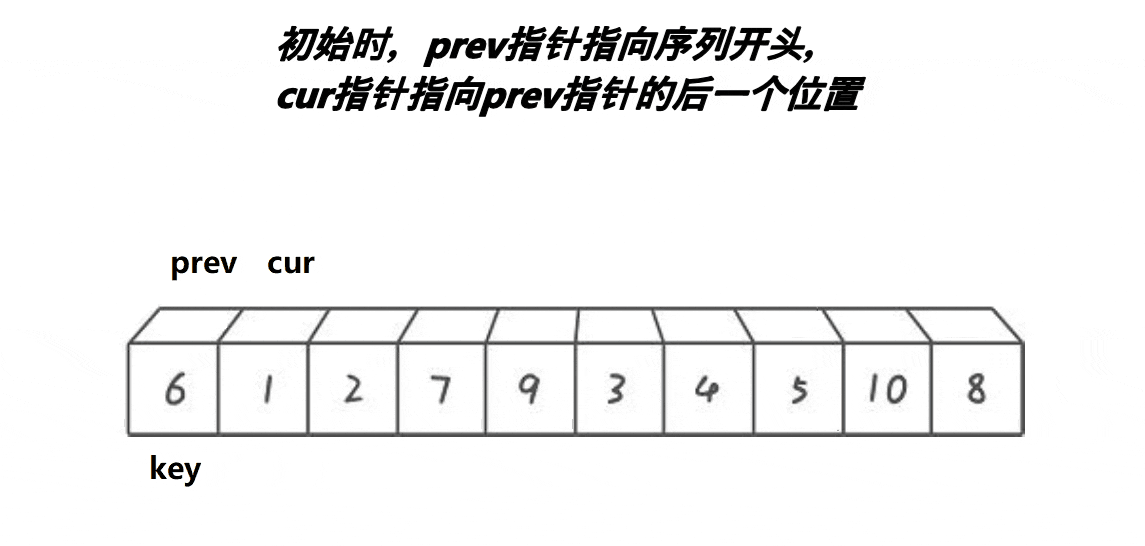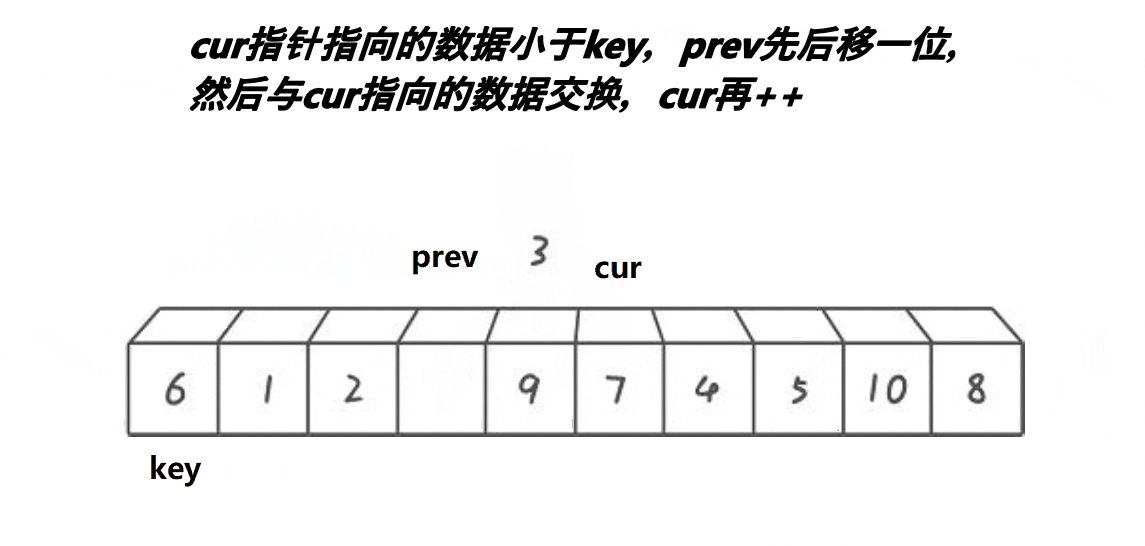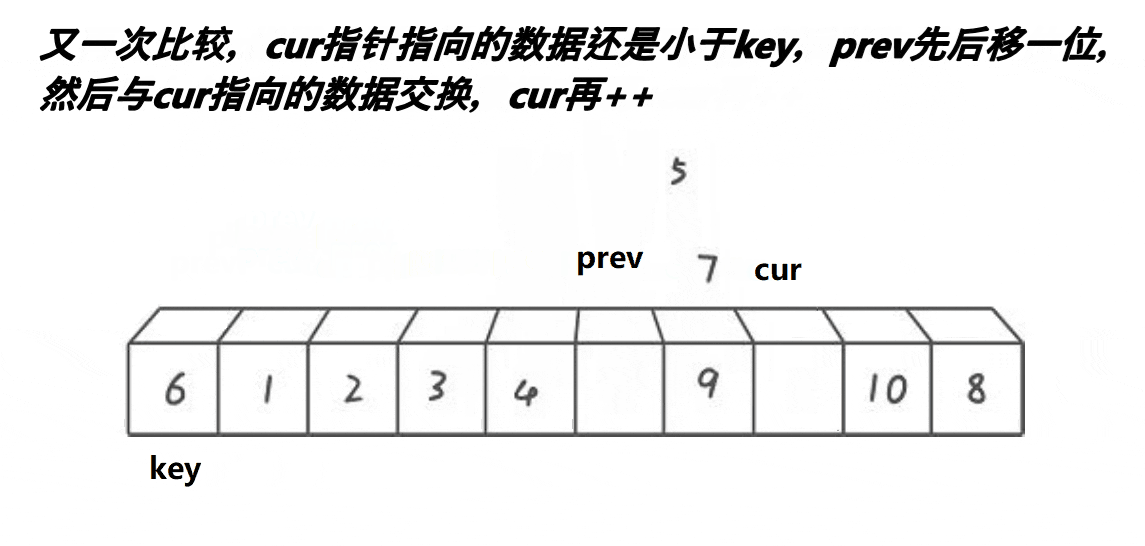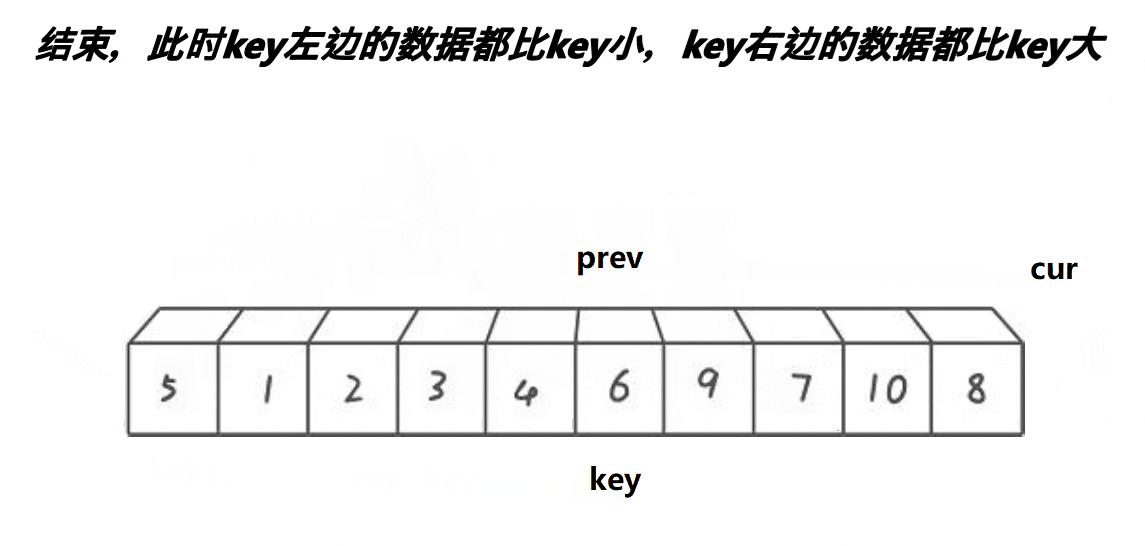
// 快速排序前后指针法
int PartSort3(int* a, int left, int right)
{int midi = GetMidi(a, left, right);Swap(&a[left], &a[midi]);int prev = left;int cur = prev + 1;int keyi = left;while (cur <= right){if (a[cur] < a[keyi] && ++prev != cur){Swap(&a[prev], &a[cur]);}++cur;}Swap(&a[prev], &a[keyi]);return prev;
}2.3.3.1 快速排序优化
- 三数取中法选key
- 递归到小的子区间时,可以考虑使用插入排序
// 三数取中
int GetMidi(int* a, int left, int right)
{int mid = (left + right) / 2;if (a[left] < a[mid]){if (a[mid] < a[right]){return mid;}else if (a[left] > a[right]) // mid是最大值{return left;}else{return right;}}else // a[left] > a[mid]{if (a[mid] > a[right]){return mid;}else if (a[left] < a[right]) // mid是最小值{return left;}else{return right;}}
}// 添加小区间优化的快速排序
void QuickSort1(int* a, int begin, int end)
{if (begin >= end)return;// 小区间优化,小区间不再递归分割排序,降低递归次数if ((end - begin + 1) > 10){int keyi = PartSort3(a, begin, end);QuickSort1(a, begin, keyi - 1);QuickSort1(a, keyi + 1, end);}else{InsertSort(a + begin, end - begin + 1);}
}2.3.3.2 快速排序非递归
void QuickSortNonR(int* a, int begin, int end)
{ST st;STInit(&st);STPush(&st, end);STPush(&st, begin);while (!STEmpty(&st)){int left = STTop(&st);STPop(&st);int right = STTop(&st);STPop(&st);int keyi = PartSort1(a, left, right);if (keyi + 1 < right){STPush(&st, right);STPush(&st, keyi + 1);}if (left < keyi - 1){STPush(&st, keyi - 1);STPush(&st, left);}}STDestroy(&st);
}快速排序的特性总结:
- 快速排序整体的综合性能和使用场景都是比较好的,所以才敢叫快速排序
- 时间复杂度:O(N*logN)
- 空间复杂度:O(logN)
- 稳定性:不稳定
2.4 归并排序
基本思想:
归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。 归并排序核心步骤:
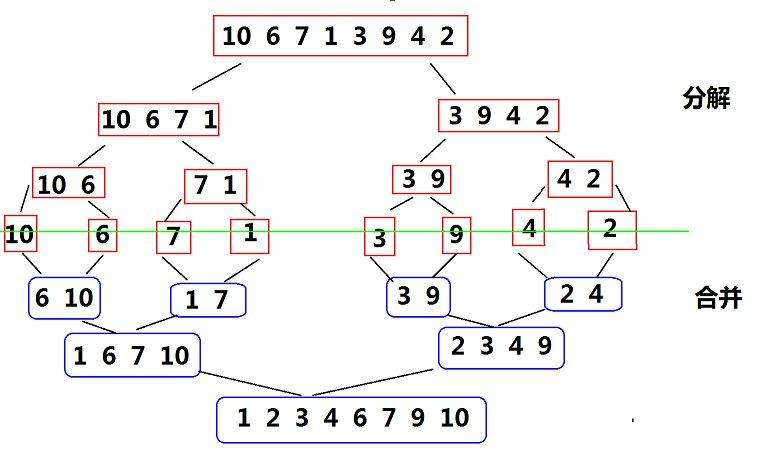
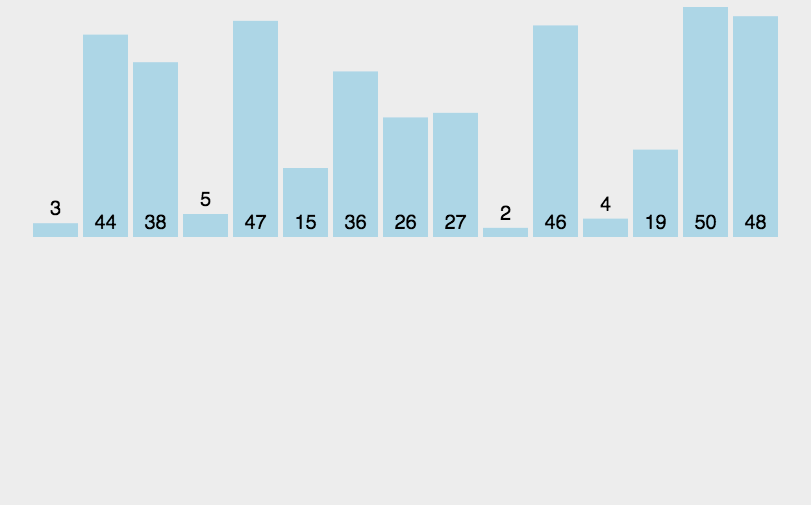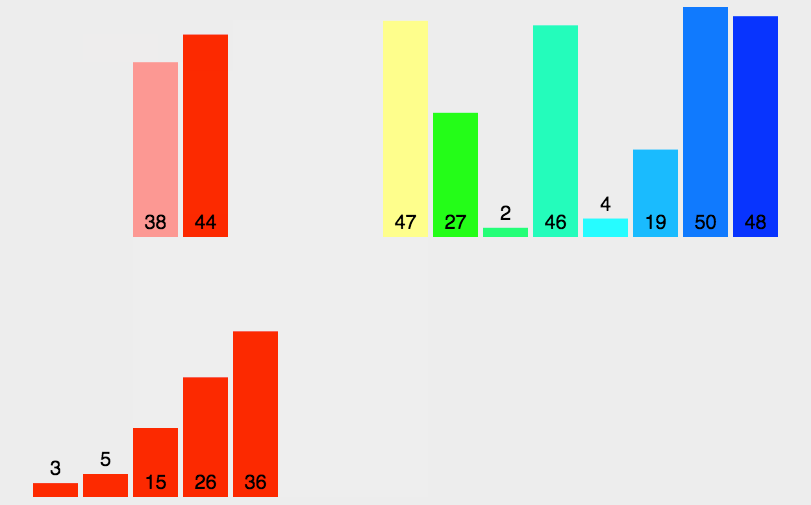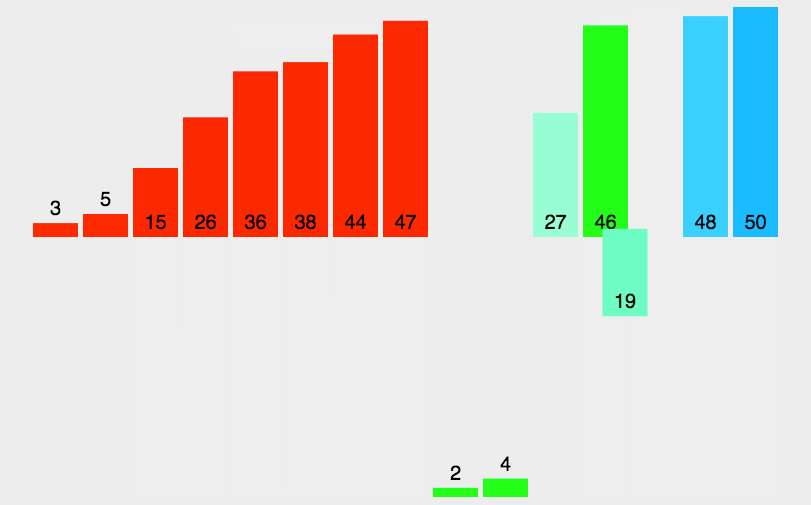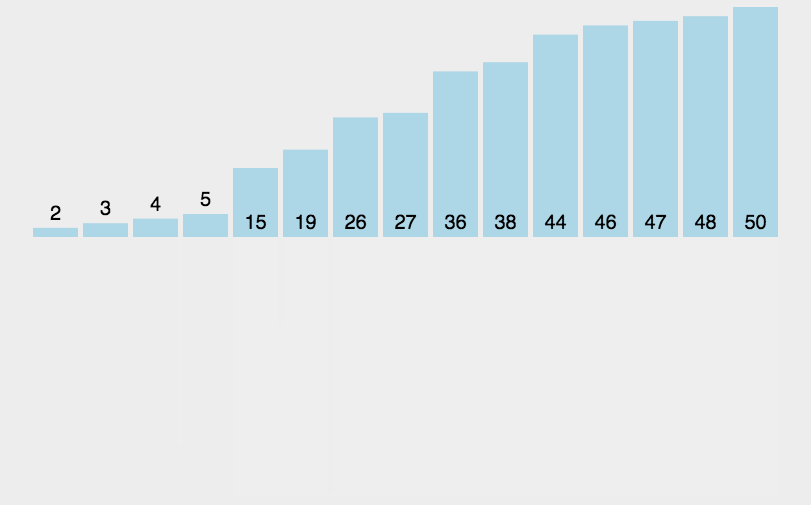
// 子函数 方便递归
void _MergeSort(int* a, int* tmp, int begin, int end)
{if (end <= begin)return;int mid = (end + begin) / 2;// [begin, mid] [mid + 1, end]_MergeSort(a, tmp, begin, mid);_MergeSort(a, tmp, mid + 1, end);// 归并到tmp数组,再拷贝回去int begin1 = begin, end1 = mid;int begin2 = mid + 1, end2 = end;int index = begin;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){tmp[index++] = a[begin1++];}else{tmp[index++] = a[begin2++];}}while (begin1 <= end1){tmp[index++] = a[begin1++];}while (begin2 <= end2){tmp[index++] = a[begin2++];}// 拷贝回原数组memcpy(a + begin, tmp + begin, (end - begin + 1) * sizeof(int));
}// 归并排序 递归实现
void MergeSort(int* a, int n)
{int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL){perror("malloc fail");return;}_MergeSort(a, tmp, 0, n - 1);free(tmp);
}// 归并排序 非递归实现
void MergeSortNonR(int* a, int n)
{int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL){perror("malloc fail");return;}int gap = 1;while (gap < n){for (int i = 0; i < n; i += 2 * gap){int begin1 = i, end1 = i + gap - 1;int begin2 = i + gap, end2 = i + 2 * gap - 1;// [begin1, end1] [begin2, end2] 归并// 如果第二组不存在,这一组不用归并了if (begin2 >= n){break;}// 如果第二组的右边界越界,修正一下if (end2 >= n){end2 = n - 1;}int index = i;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){tmp[index++] = a[begin1++];}else{tmp[index++] = a[begin2++];}}while (begin1 <= end1){tmp[index++] = a[begin1++];}while (begin2 <= end2){tmp[index++] = a[begin2++];}// 拷贝回原数组memcpy(a + i, tmp + i, (end2 - i + 1) * sizeof(int));}gap *= 2;}free(tmp);
}归并排序的特性总结:
- 归并的缺点在于需要O(N)的空间复杂度,归并排序的思考更多的是解决在磁盘中的外排序问题。
- 时间复杂度:O(N*logN)
- 空间复杂度:O(N)
- 稳定性:稳定
2.5 非比较排序
思想:计数排序又称为鸽巢原理,是对哈希直接定址法的变形应用。 操作步骤:
- 统计相同元素出现次数
- 根据统计的结果将序列回收到原来的序列中
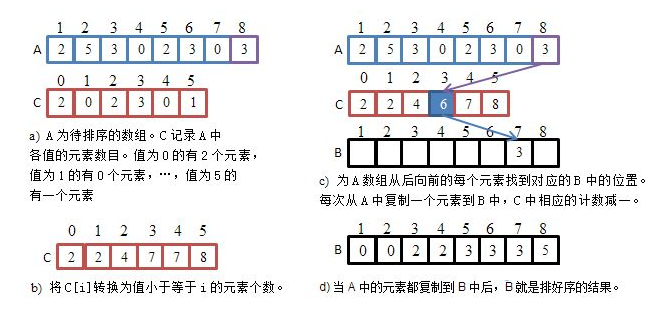
// 计数排序
void CountSort(int* a, int n)
{int min = a[0], max = a[0];for (int i = 0; i < n; i++){if (a[i] < min)min = a[i];if (a[i] > max)max = a[i];}int range = max - min + 1;int* count = (int*)malloc(sizeof(int) * range);printf("range:%d\n", range);if (count == NULL){perror("malloc fail");return;}memset(count, 0, sizeof(int) * range);// 统计数据出现次数for (int i = 0; i < n; i++){count[a[i] - min]++;}// 排序int j = 0;for (int i = 0; i < range; i++){while (count[i]--){a[j++] = i + min;}}
}计数排序的特性总结:
- 计数排序在数据范围集中时,效率很高,但是适用范围及场景有限。
- 时间复杂度:O(MAX(N, 范围))
- 空间复杂度:O(范围)
- 稳定性:稳定
3. 排序算法复杂度及稳定性分析
| 排序方法 | 平均情况 | 最好情况 | 最坏情况 | 辅助空间 | 稳定性 |
|---|---|---|---|---|---|
| 冒泡排序 | 稳定 | ||||
| 简单选择排序 | 不稳定 | ||||
| 直接插入排序 | 稳定 | ||||
| 希尔排序 | 不稳定 | ||||
| 堆排序 | 不稳定 | ||||
| 归并排序 | 稳定 | ||||
| 快速排序 | 不稳定 |
本文完
相关文章:
【数据结构】八大排序
目录 1. 排序的概念及其作用 1.1 排序的概念 1.2 排序运用 1.3 常见的排序算法 2. 常见排序算法的实现 2.1 插入排序 2.1.1 基本思想 2.1.2 直接插入排序 2.1.3 希尔排序(缩小增量排序) 2.2 选择排序 2.2.1 基本思想 2.2.2 直接选择排序 2.2…...

MYSQL(事务+锁+MVCC+SQL执行流程)理解
一)事务的特性: 一致性:主要是在数据层面来说,不能说执行扣减库存的操作的时候用户订单数据却没有生成 原子性:主要是在操作层面来说,要么操作完成,要么操作全部回滚; 隔离性:是自己的事务操作自己的数据,不会受到到其…...
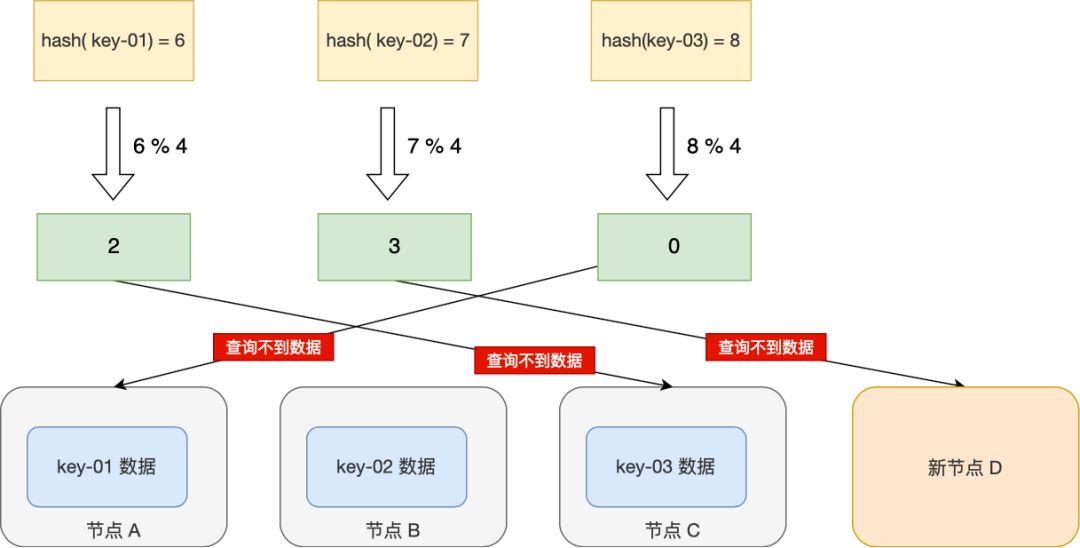
解密一致性哈希算法:实现高可用和负载均衡的秘诀
解密一致性哈希算法:实现高可用和负载均衡的秘诀 前言第一:分布式系统中的数据分布问题,为什么需要一致性哈希算法第二:一致性hash算法的原理第三:一致性哈希算法的优点和局限性第四:一致性哈希算法的安全性…...

Python脚本:让工作自动化起来
Python是一种流行的编程语言,以其简洁和易读性而闻名。它提供了大量的库和模块,使其成为自动化各种任务的绝佳选择。 本文将探讨Python脚本及其代码,可以帮助您自动化各种任务并提高工作效率。无论您是开发人员、数据分析师还是只是想简化工…...

香港科技大学广州|可持续能源与环境学域博士招生宣讲会—广州大学城专场!!!(暨全额奖学金政策)
香港科技大学广州|可持续能源与环境学域博士招生宣讲会—广州大学城专场!!!(暨全额奖学金政策) “面向未来改变游戏规则的——可持续能源与环境学域” ���专注于能源环…...
uni-app:多种方法写入图片路径
一、文件在前端文件夹中 1、相对路径引用 从当前文件所在位置开始寻找图片文件的路径。../../ 表示返回两级目录,即从当前文件所在的 wind.vue 所在的位置开始向上回退两级。接着,进入 static 目录,再进入 look 目录,最后定位到 …...

共谋工业3D视觉发展,深眸科技以自研解决方案拓宽场景应用边界
随着中国工业领域自动化程度逐渐攀升,“机器换人”这一需求进一步提升。在传统2D工业视觉易受环境光干扰、无法进一步获取物体深度信息的限制条件下,工业3D视觉凭借着更强的空间和深度感知能力,以及通过点云数据获取物体距离和三维坐标信息的…...

前端面试基础面试题——11
1.什么是 vue 的计算属性? 2.vue怎么实现页面的权限控制 3.watch的作用是什么 4.响应式系统的基本原理 5.vue-loader 是什么?使用它的用途有哪些? 6.vuex 工作原理详解 7.vuex 有哪几种属性? 8.什么是 MVVM? 9…...
)
SQL server中内连接和外连接的区别、表达(表的连接)
SQL server中内连接与外连接的区别、表达 区别表达内连接外连接 待续 首先,内连接和外连接都是对表的连接操作 区别 内连接:连接结果仅包含符合连接条件的行,其中至少一个属性是共同的;注意区分在嵌套查询时使用的any以及all的区…...
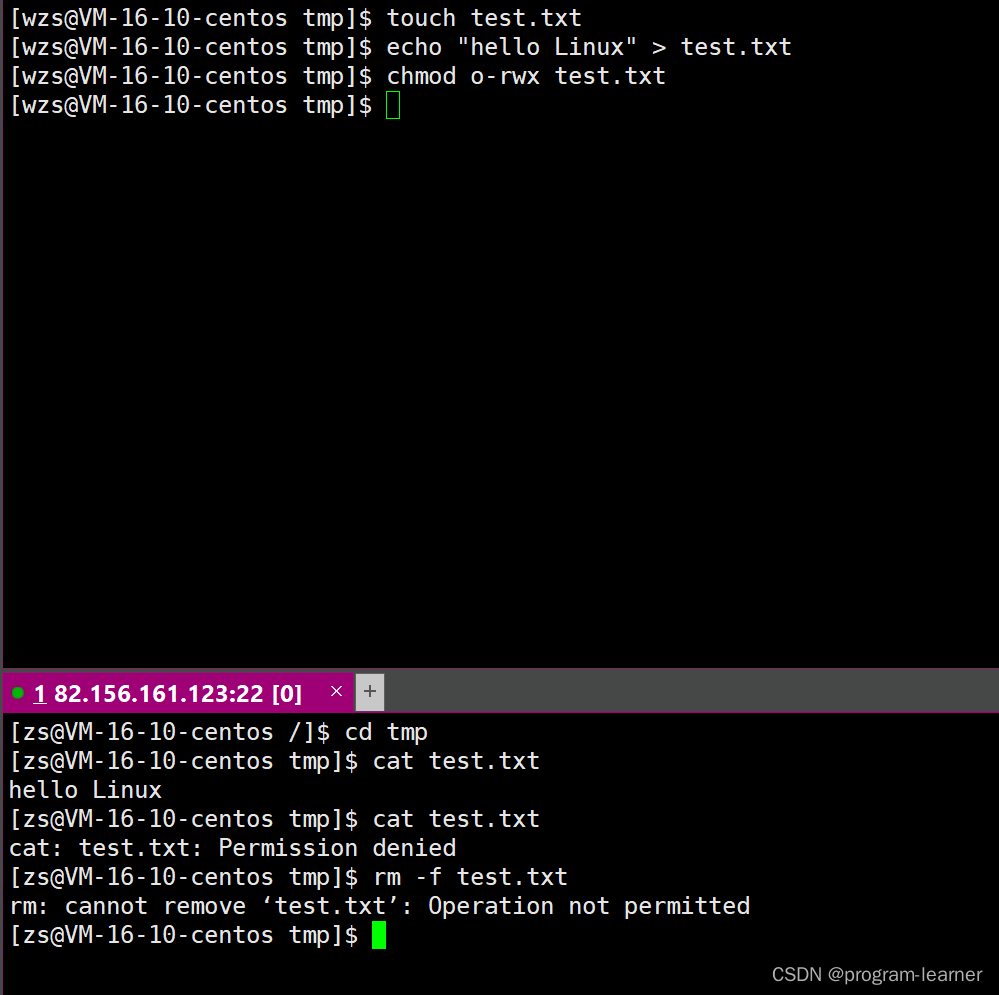
Linux中的shell外壳与权限(包含目录文件的权限,粘滞位的来龙去脉)
Linux中的shell外壳与权限[包含目录文件的权限,粘滞位的来龙去脉] 一.shell外壳的理解1.为什么需要有shell外壳的存在?2.什么是shell外壳?3.shell外壳的运行原理是什么?4.shell和bash的关系 二.Linux中的用户权限1.用户分类与身份切换1.用户分类2.root用户切换为普通用户1.s…...

力扣第45题 跳跃游戏II c++ 贪心算法
题目 45. 跳跃游戏 II 中等 相关标签 贪心 数组 动态规划 给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。 每个元素 nums[i] 表示从索引 i 向前跳转的最大长度。换句话说,如果你在 nums[i] 处,你可以跳转到任意 nums[i j] 处…...

1024动态
感叹一下当前行情 从事码农这些年今年是最难的一年...
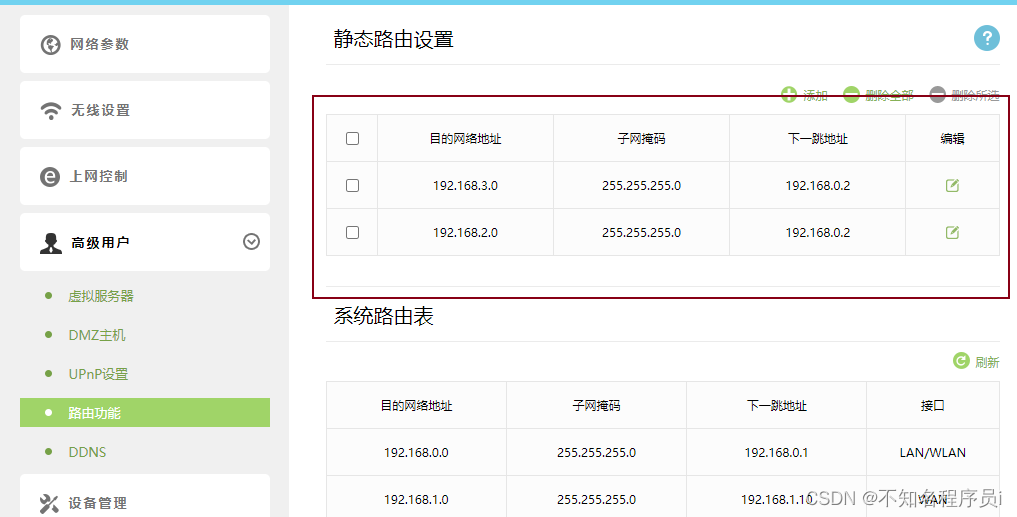
中心胖AP(AD9430DN)+远端管理单元RU(R240D)+出口网关,实现组网
适用于:V200R008至V200R019C00版本的万兆中心胖AP(AD9431DN-24X)。 组网规划 RU管理:VLAN 100,网段为192.168.100.0/24。 无线业务:VLAN 3,SSID为“wlan-net”,密码为“88888888”…...

shell_45.Linux在脚本中使用 getopt
在脚本中使用 getopt $ cat extractwithgetopt.sh #!/bin/bash # Extract command-line options and values with getopt # set -- $(getopt -q ab:cd "$") # echo while [ -n "$1" ] do case "$1" in -a) echo "Found the -a opt…...

2023-8-20 CVTE视源股份后端开发实习一面
自我介绍 操作系统 1 有了解进程和线程的特点吗 2 在linux层面的话是怎么创建一个进程或者一个线程的(具体的系统调用的命令) 答: 3 如果是java层面讲,怎么去启动一个线程,要实现哪些方法呢 Thread类实现run()方法的…...
二叉树进阶
欢迎来到Cefler的博客😁 🕌博客主页:那个传说中的man的主页 🏠个人专栏:题目解析 🌎推荐文章:题目大解析(3) 目录 👉🏻二叉搜索树概念 Ǵ…...
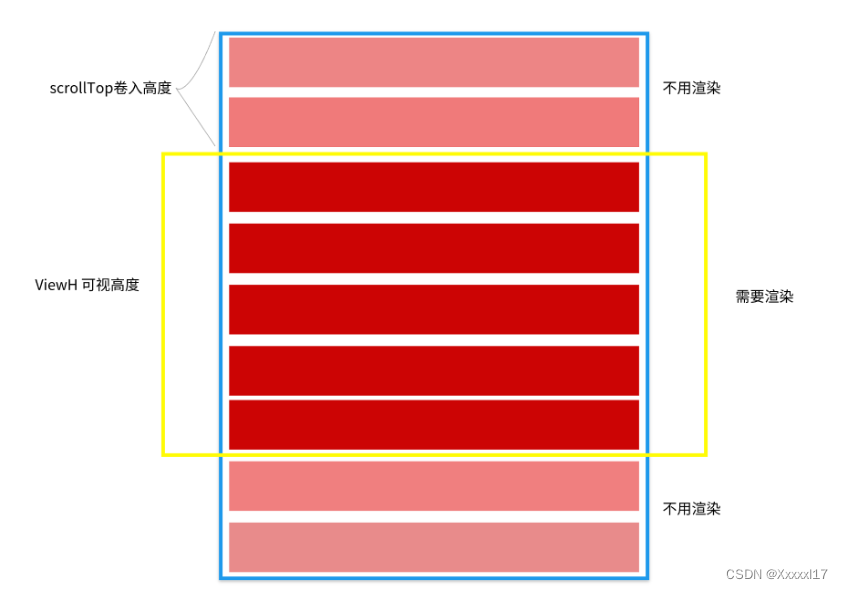
前端性能优化 - 虚拟滚动
一 需求背景 需求:在一个表格里面一次性渲染全部数据,不采用分页形式,每行数据都有Echart图插入。 问题:图表渲染卡顿 技术栈:Vue、Element UI 卡顿原因:页面渲染时大量的元素参与到了重排的动作中&#x…...
手写 Promise(1)核心功能的实现
一:什么是 Promise Promise 是异步编程的一种解决方案,其实是一个构造函数,自己身上有all、reject、resolve这几个方法,原型上有then、catch等方法。 Promise对象有以下两个特点。 (1)对象的状态不受…...

深入探究Java内存模型
文章目录 🌟 Java虚拟机内存模型🍊 一、方法区🍊 二、堆🎉 堆的基本概念🎉 堆的结构📝 新生代📝 老年代 🎉 堆的分配策略📝 对象优先分配📝 空间优先分配 &am…...

深度学习 | Pytorch深度学习实践 (Chapter 10、11 CNN)
十、CNN 卷积神经网络 基础篇 首先引入 —— 二维卷积:卷积层保留原空间信息关键:判断输入输出的维度大小特征提取:卷积层、下采样分类器:全连接 引例:RGB图像(栅格图像) 首先,老师…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

MinIO Docker 部署:仅开放一个端口
MinIO Docker 部署:仅开放一个端口 在实际的服务器部署中,出于安全和管理的考虑,我们可能只能开放一个端口。MinIO 是一个高性能的对象存储服务,支持 Docker 部署,但默认情况下它需要两个端口:一个是 API 端口(用于存储和访问数据),另一个是控制台端口(用于管理界面…...
)
安卓基础(Java 和 Gradle 版本)
1. 设置项目的 JDK 版本 方法1:通过 Project Structure File → Project Structure... (或按 CtrlAltShiftS) 左侧选择 SDK Location 在 Gradle Settings 部分,设置 Gradle JDK 方法2:通过 Settings File → Settings... (或 CtrlAltS)…...

SpringAI实战:ChatModel智能对话全解
一、引言:Spring AI 与 Chat Model 的核心价值 🚀 在 Java 生态中集成大模型能力,Spring AI 提供了高效的解决方案 🤖。其中 Chat Model 作为核心交互组件,通过标准化接口简化了与大语言模型(LLM࿰…...


