368周赛leetcode
1 2题元素和最小的山形三元组
经典动规
题目内容
给你一个下标从 0 开始的整数数组 nums 。
如果下标三元组 (i, j, k) 满足下述全部条件,则认为它是一个 山形三元组 :
i < j < k
nums[i] < nums[j] 且 nums[k] < nums[j]
请你找出 nums 中 元素和最小 的山形三元组,并返回其 元素和 。如果不存在满足条件的三元组,返回 -1 。
样例
输入:nums = [5,4,8,7,10,2]
输出:13
解释:三元组 (1, 3, 5) 是一个元素和等于 13 的山形三元组,因为:
- 1 < 3 < 5
- nums[1] < nums[3] 且 nums[5] < nums[3]
这个三元组的元素和等于 nums[1] + nums[3] + nums[5] = 13 。可以证明不存在元素和小于 13 的山形三元组。
数据范围
3 <= nums.length <= 105
1 <= nums[i] <= 108
思路
左右算最小值点,记录,然后动态规划
复杂度O(n)。
class Solution {public int minimumSum(int[] nums) {int n = nums.length;int[] left_min = new int[n];int[] right_min = new int[n];int min = nums[0];for(int i=1;i<n-1;i++){min=Math.min(min,nums[i-1]);left_min[i] = min;}min = nums[n-1];for(int i=n-2;i>0;i--){min=Math.min(min,nums[i+1]);right_min[i] = min;}int result = Integer.MAX_VALUE;for(int i=1;i<n-1;i++)if(nums[i]>left_min[i]&&nums[i]>right_min[i])result = Math.min(result,nums[i]+left_min[i]+right_min[i]);return result==Integer.MAX_VALUE?-1:result;}
}
3 题 元素和最小的山形三元组
题目内容
给你一个长度为 n 下标从 0 开始的整数数组 nums 。
我们想将下标进行分组,使得 [0, n - 1] 内所有下标 i 都 恰好 被分到其中一组。
如果以下条件成立,我们说这个分组方案是合法的:
对于每个组 g ,同一组内所有下标在 nums 中对应的数值都相等。
对于任意两个组 g1 和 g2 ,两个组中 下标数量 的 差值不超过 1 。
请你返回一个整数,表示得到一个合法分组方案的 最少 组数。
样例
示例 1:
输入:nums = [3,2,3,2,3]
输出:2
解释:一个得到 2 个分组的方案如下,中括号内的数字都是下标:
组 1 -> [0,2,4]
组 2 -> [1,3]
所有下标都只属于一个组。
组 1 中,nums[0] == nums[2] == nums[4] ,所有下标对应的数值都相等。
组 2 中,nums[1] == nums[3] ,所有下标对应的数值都相等。
组 1 中下标数目为 3 ,组 2 中下标数目为 2 。
两者之差不超过 1 。
无法得到一个小于 2 组的答案,因为如果只有 1 组,组内所有下标对应的数值都要相等。
所以答案为 2 。
示例 2:
输入:nums = [10,10,10,3,1,1]
输出:4
解释:一个得到 2 个分组的方案如下,中括号内的数字都是下标:
组 1 -> [0]
组 2 -> [1,2]
组 3 -> [3]
组 4 -> [4,5]
分组方案满足题目要求的两个条件。
无法得到一个小于 4 组的答案。
所以答案为 4 。
范围
1 <= nums.length <= 105
1 <= nums[i] <= 109
思路
先记录nums的值进行一个每个数出现次数进行排序,生成数组members
然后根据出现次数来获取可以组成的最小组数
这里 从出现次数的最小值遍历到1,遍历选取当前值和当前值+1(now和now+1)。然后对members数组进行判断、遍历、加和答案。
复杂度: O ( n ) O(n) O(n)
ac代码
class Solution {public int isgroup(int member,int now){int result = Integer.MAX_VALUE;for(int i=0;i<2;i++){if(now+i<=0)continue;int remain = now+i;int group = member/remain;int leave = member%remain;if(leave==0)result = Math.min(group,result);else{int remeber = member - group*remain;if(i==0&&remeber<=group)result = Math.min(group,result);if(i==1&&((remain-remeber)<=group))result = Math.min(group+1,result);}}return result;}public int minGroupsForValidAssignment(int[] nums) {HashMap<Integer,Integer> map = new HashMap<>();int now=0;for(int x:nums){now = map.getOrDefault(x,0);map.put(x,now+1);}int[] members = new int[map.size()];now = 0;for(Map.Entry<Integer,Integer> x:map.entrySet())members[now++] = x.getValue();Arrays.sort(members);int max_num = members[0];for(int i=max_num;i>0;i--){int result = 0;for(now=0;now<members.length;now++){int group_num = isgroup(members[now],i);System.out.println(group_num+" "+i);if(group_num == Integer.MAX_VALUE)break;result+=group_num;}if(now==members.length)return result;}return -1;}
}
4 6920. 得到 K 个半回文串的最少修改次数
未完成
相关文章:

368周赛leetcode
1 2题元素和最小的山形三元组 经典动规 题目内容 给你一个下标从 0 开始的整数数组 nums 。 如果下标三元组 (i, j, k) 满足下述全部条件,则认为它是一个 山形三元组 : i < j < k nums[i] < nums[j] 且 nums[k] < nums[j] 请你找出 num…...

Vue 的 nextTick:深入理解异步更新机制
目录 一、前言 二、Vue.js 异步更新机制简述 三、Vue.nextTick原理 四、nextTick 的应用场景 1. 获取更新后的 DOM 元素 2. 在 DOM 更新后执行自定义的回调函数 3. 解决事件监听器中的更新问题 五、Vue.nextTick与其他异步更新方法的比较 六、总结 一、前言 Vue.js&a…...
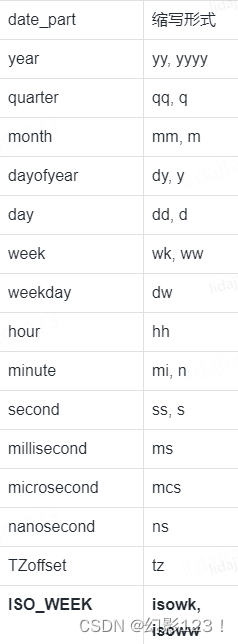
SQL关于日期的计算合集
前言 在SQL Server中,时间和日期是常见的数据类型,也是数据处理中重要的一部分。SQL Server提供了许多内置函数,用于处理时间和日期数据类型。这些函数可以帮助我们执行各种常见的任务,例如从日期中提取特定的部分,计…...

shell_44.Linux使用 getopt 命令
使用 getopt 命令 getopt 命令在处理命令行选项和参数时非常方便。它能够识别命令行参数,简化解析过程 1. 命令格式 getopt 命令可以接受一系列任意形式的命令行选项和参数,并自动将其转换成适当的格式。 getopt 的命令格式如下: getopt opt…...

Linux备份Docker的mysql数据并传输到其他服务器保证数据级容灾
目录 简介什么是容灾 ?容灾的分类容灾和备份有什么连系 ? 数据级容灾备份步骤1、scp命令:用于Linux之间复制文件和目录2、编写备份数据库脚本3、crontab定时任务执行脚本4、测试 应用级容灾业务级容灾 简介 为了防止客户系统的数据丢失&…...

【vue+nestjs】qq第三方授权登录【超详细】
项目场景: 前端使用vue3ts 后端使用nestjs 1.申请appId,appKey 1.进入qq互联官网。创建应用 特别注意 1.在填写网站回调域时,需要你线上真实能访问的。不然审核不通过。我的回调地址是前端路由地址 2.如果你想本地调试,回调到你的线上地址。你可以在本…...
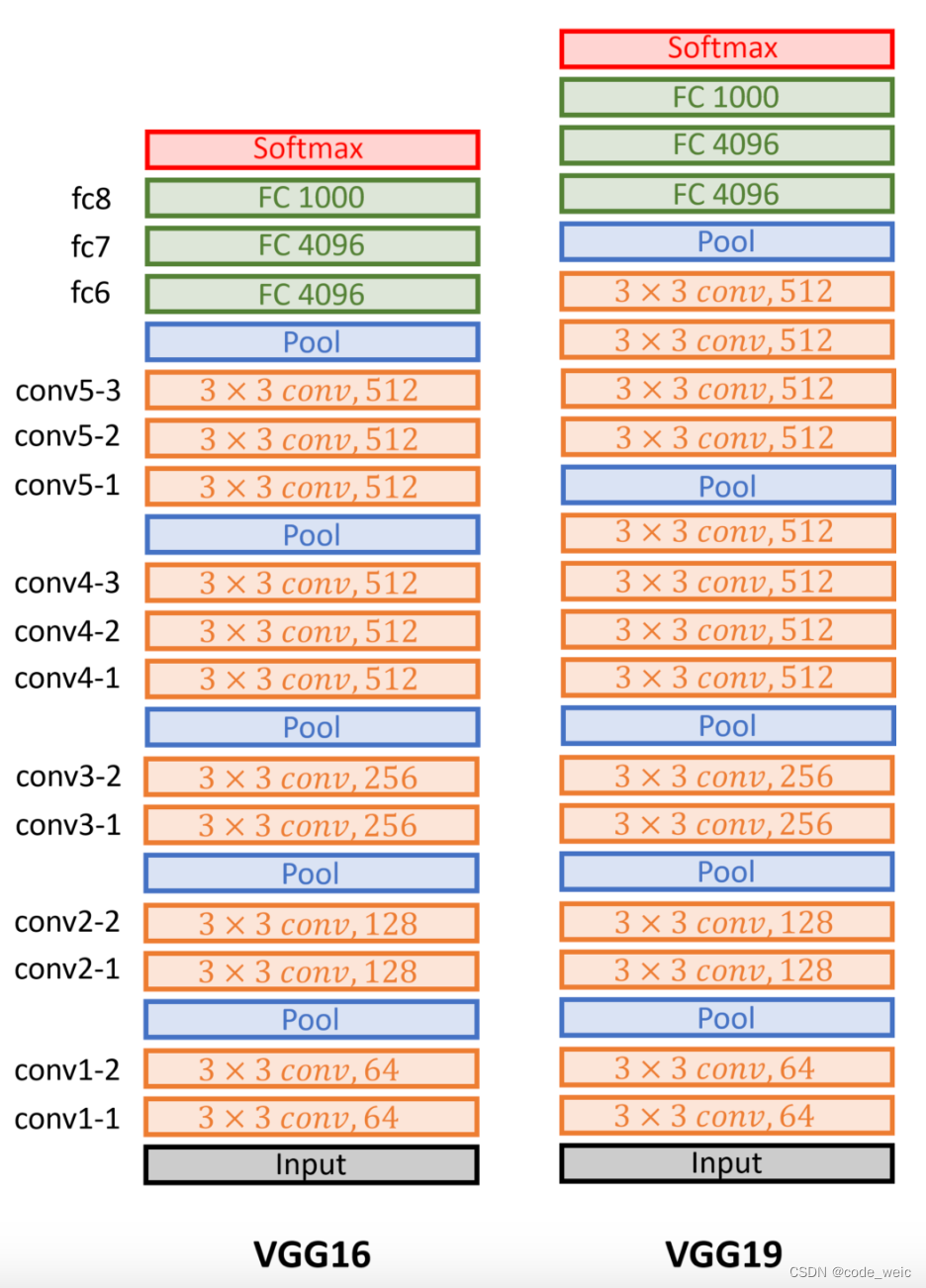
经典卷积神经网络 - VGG
使用块的网络 - VGG。 使用多个 3 3 3\times 3 33的要比使用少个 5 5 5\times 5 55的效果要好。 VGG全称是Visual Geometry Group,因为是由Oxford的Visual Geometry Group提出的。AlexNet问世之后,很多学者通过改进AlexNet的网络结构来提高自己的准确…...
/系统测试(ST)/用户验收测试(UAT))
系统集成测试(SIT)/系统测试(ST)/用户验收测试(UAT)
文章目录 单元测试集成测试系统测试用户验收测试黑盒测试白盒测试压力测试性能测试容量测试安全测试SIT和UAT的区别 单元测试 英文 unit testing,缩写 UT。测试粒度最小,一般由开发小组采用白盒方式来测试,主要测试单元是否符合“设计”。 …...

Android Gradle8.0以上多渠道写法以及针对不同渠道导入包的方式,填坑!
目录 多渠道的写法 针对多渠道引用不同的包 There was a failure while populating the build operation queue: Could not stat file E:\xxxx\xxxx\xxxx\app\src\UAT\libsUAT\xxx-provider(?)-xx.aar 最近升级了Gradle8.3之后,从Groovy 迁移到 Kotlinÿ…...
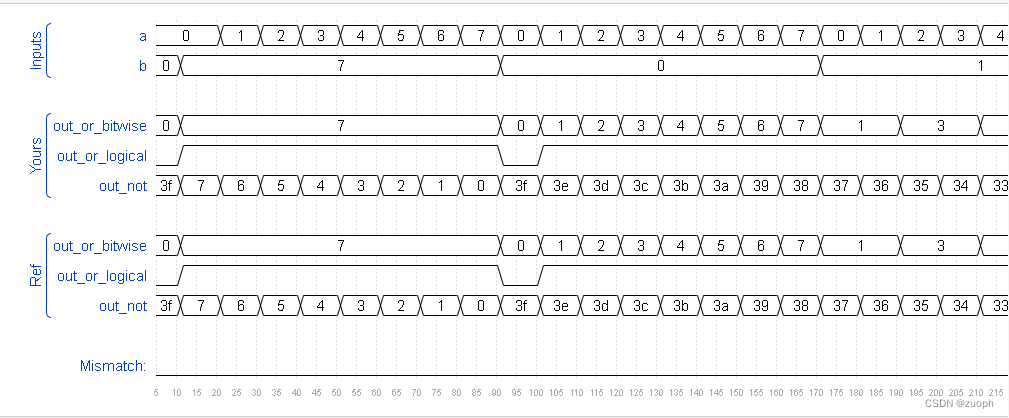
hdlbits系列verilog解答(向量门操作)-14
文章目录 一、问题描述二、verilog源码三、仿真结果 一、问题描述 构建一个具有两个 3 位输入的电路,用于计算两个向量的按位 OR、两个向量的逻辑 OR 以及两个向量的逆 (NOT)。将b反相输出到out_not上半部分,将a 的反相输出到out…...
)
工厂模式(初学)
工厂模式 1、简单工厂模式 是一种创建型设计模式,旨在通过一个工厂类(简单工厂)来封装对象的实例化过程 运算类 public class Operation { //这个是父类private double num1; //运算器中的两个值private double num2;public double getNu…...

python试题实例
背景: 在外地出差,突然接到单位电话,让自己出一些python考题供新人教育训练使用,以下是10道Python编程试题及其答案: 1.试题:请写一个Python程序,计算并输出1到100之间所有偶数的和。 答案&am…...
)
Java Heap Space问题解析与解决方案(InsCode AI 创作助手)
Heap Space问题是Java开发中常见的内存溢出问题之一,我们需要理解其原因和表现形式,然后通过优化代码、增加JVM内存和使用垃圾回收机制等方法来解决。 一、常见报错 java.lang.OutOfMemoryError: Java heap space二、Heap Space问题的原因 对象创建过…...
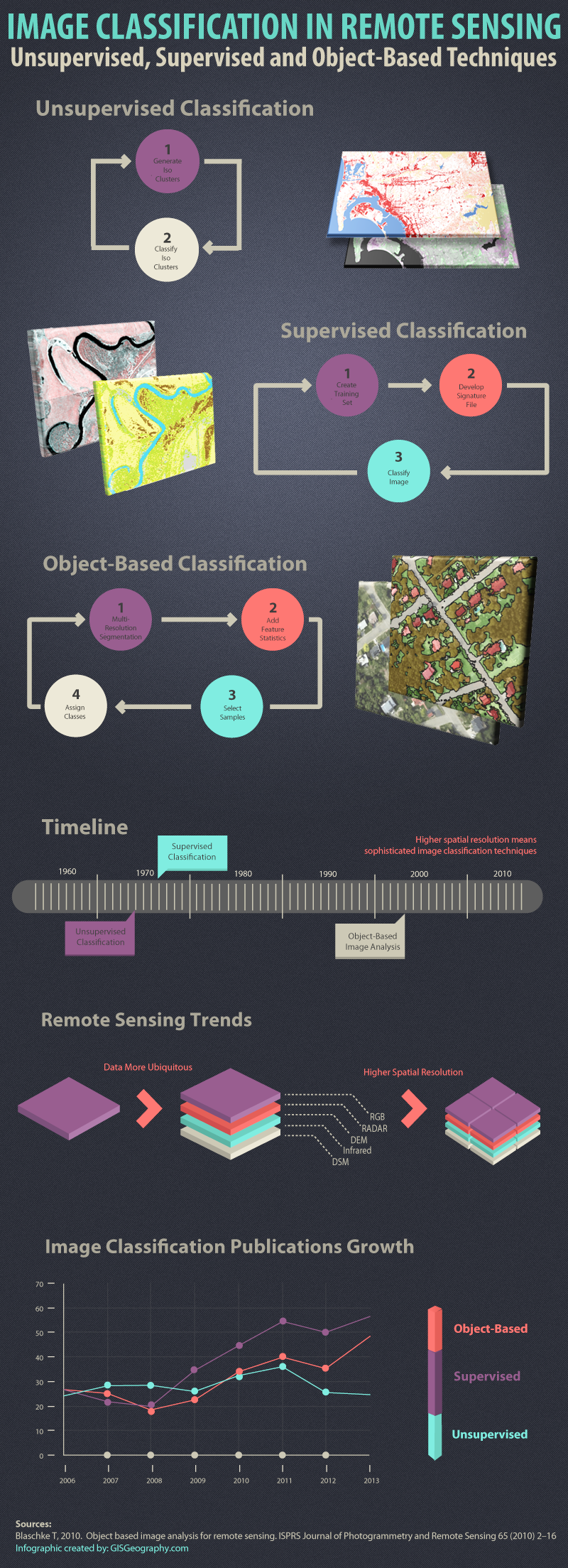
基于遥感影像的分类技术(监督/非监督和面向对象的分类技术)
遥感图像分类技术 “图像分类是将土地覆盖类别分配给像素的过程。例如,类别包括水、城市、森林、农业和草原。”前言 – 人工智能教程 什么是遥感图像分类? 遥感图像分类技术的三种主要类型是: 无监督图像分类监督图像分类基于对象的图像分析…...
 方法)
插入兄弟元素 insertAfter() 方法
insertAfter() 方法在被选元素后插入 HTML 元素。 提示:如需在被选元素前插入 HTML 元素,请使用 insertBefore() 方法。 语法 $(content).insertAfter(selector)例子: $("<span>Hello world!</span>").insertAfter(…...

【C++项目】高并发内存池第二讲中心缓存CentralCache框架+核心实现
CentralCache 1.框架介绍2.核心功能3.核心函数实现介绍3.1SpanSpanList介绍3.2CentralCache.h3.3CentralCache.cpp3.4TreadCache申请内存函数介绍3.5慢反馈算法 1.框架介绍 回顾一下ThreadCache的设计: 如图所示,ThreadCache设计是一个哈希桶结构&…...
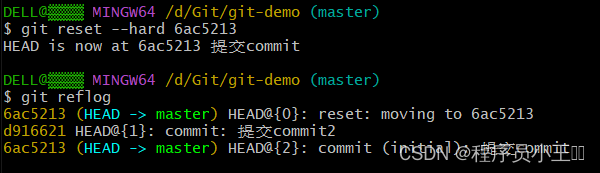
Git基础教程
一、Git简介 1、什么是Git? Git是一个开源的分布式版本控制系统,用于敏捷高效地处理任何或大或小的项目。 Git是Linus Torvalds为了帮助管理Linux内核开发而开发的一个开放源代码的版本控制软件。 Git与常用的版本控制工具CVS、Subversion等不同&#…...
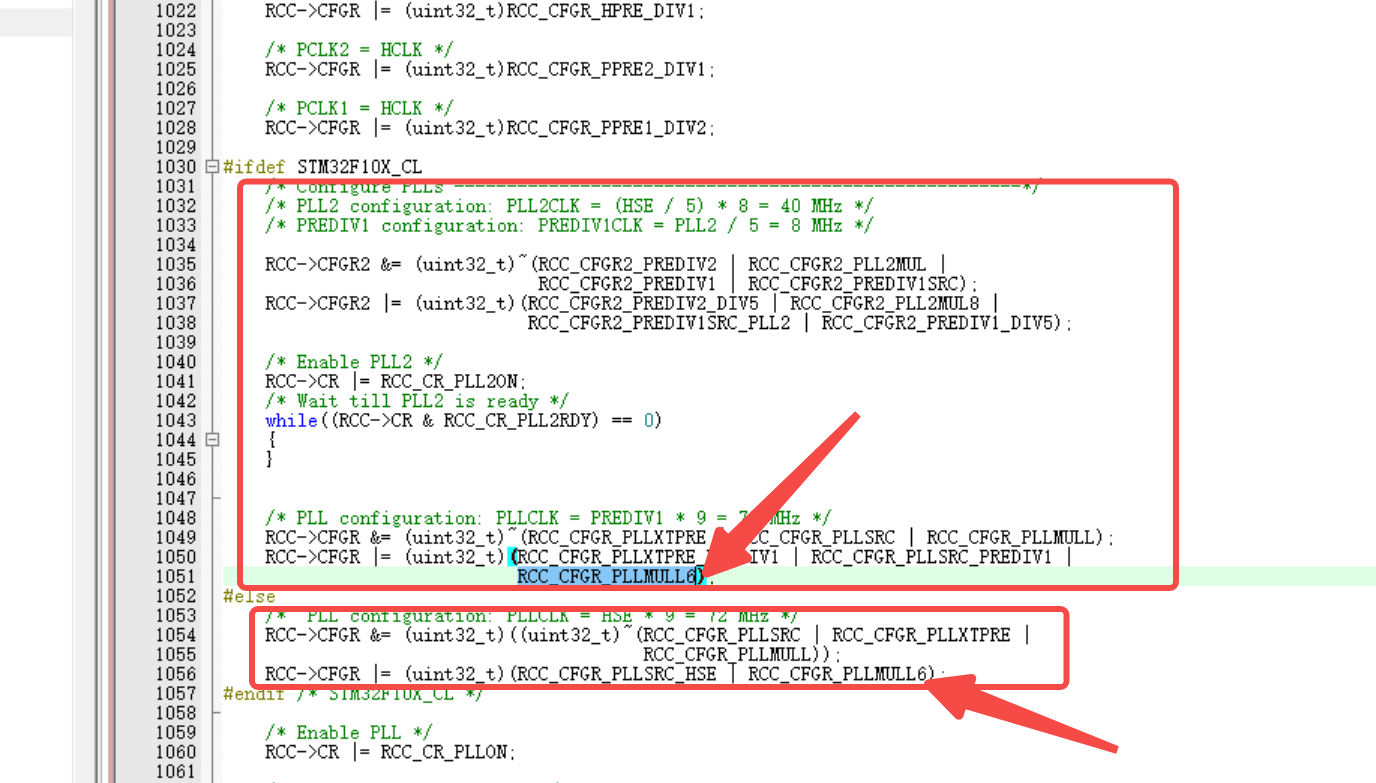
stm32外部时钟为12MHZ,修改代码适配
代码默认是8MHZ的,修改2个地方: 第一个地方是这个文件的这里: 第二个地方是找到这个函数: 修改第二个地方的这里:...
【数据结构】八大排序
目录 1. 排序的概念及其作用 1.1 排序的概念 1.2 排序运用 1.3 常见的排序算法 2. 常见排序算法的实现 2.1 插入排序 2.1.1 基本思想 2.1.2 直接插入排序 2.1.3 希尔排序(缩小增量排序) 2.2 选择排序 2.2.1 基本思想 2.2.2 直接选择排序 2.2…...

MYSQL(事务+锁+MVCC+SQL执行流程)理解
一)事务的特性: 一致性:主要是在数据层面来说,不能说执行扣减库存的操作的时候用户订单数据却没有生成 原子性:主要是在操作层面来说,要么操作完成,要么操作全部回滚; 隔离性:是自己的事务操作自己的数据,不会受到到其…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...
