力扣第55题 跳跃游戏 c++ 贪心 + 覆盖 加暴力超时参考
题目
55. 跳跃游戏
中等
相关标签
贪心 数组 动态规划
给你一个非负整数数组 nums ,你最初位于数组的 第一个下标 。数组中的每个元素代表你在该位置可以跳跃的最大长度。
判断你是否能够到达最后一个下标,如果可以,返回 true ;否则,返回 false 。
示例 1:
输入:nums = [2,3,1,1,4] 输出:true 解释:可以先跳 1 步,从下标 0 到达下标 1, 然后再从下标 1 跳 3 步到达最后一个下标。
示例 2:
输入:nums = [3,2,1,0,4] 输出:false 解释:无论怎样,总会到达下标为 3 的位置。但该下标的最大跳跃长度是 0 , 所以永远不可能到达最后一个下标。
提示:
1 <= nums.length <= 1040 <= nums[i] <= 105
思路和解题方法
- 首先,我们维护一个变量
cover,表示当前能够覆盖的最远距离。如果数组只有一个元素,则一定可以到达终点,直接返回true。- 然后,我们从位置0开始遍历数组,遍历范围是当前可覆盖范围内的所有位置,包括位置i。在遍历过程中,不断更新
cover,使其取最大值。- 如果在遍历过程中发现
cover已经覆盖了数组的最后一个位置(即cover >= nums.size() - 1),则说明可以到达终点,直接返回true。- 如果最终没有到达终点,则说明无法到达,返回
false。
复杂度
时间复杂度:
O(n)
时间复杂度是O(n),其中n是输入数组的长度。这是因为我们只需要一次遍历数组即可完成判断。
空间复杂度
O(1)
空间复杂度是O(1),即常数级别的额外空间。除了几个变量(
cover、i)以及函数返回值外,代码并没有使用额外的数组或数据结构来存储中间结果。因此,空间复杂度是常数级别的。
c++ 代码
class Solution {
public:bool canJump(vector<int>& nums) {int cover = 0; // 当前能够覆盖的最远距离if (nums.size() == 1) return true; // 如果只有一个元素,则一定可以到达for (int i = 0; i <= cover; i++) { // 遍历当前可覆盖范围内的所有位置// 注意这里的等于号,因为 i 指的是当前位置,所以必须要考虑到 i 也可以到达cover = max(i + nums[i], cover); // 更新能够覆盖的最远距离// 这里的 max 函数是为了保证更新后的 cover 是最大的if (cover >= nums.size() - 1) return true; // 如果当前能够覆盖的最远距离已经覆盖了终点,则说明可以到达终点}return false; // 如果最后还没有到达终点,则说明无法到达}
};
本人试过了O(n*n)的代码,超出时间限制了
具体暴力的代码(c++)
class Solution {
public:bool canJump(vector<int>& nums) {int n = nums.size();vector<bool> canReach(n, false); // 创建一个长度为n的数组,初始值都为falsecanReach[0] = true; // 初始位置可达for (int i = 0; i < n; i++) {if (!canReach[i]) continue; // 如果当前位置不可达,则跳过int maxJump = min(i + nums[i], n - 1); // 当前位置最远能跳到的位置for (int j = i + 1; j <= maxJump; j++) {canReach[j] = true; // 将可达位置标记为true}}return canReach[n - 1]; // 返回最后一个位置是否可达}
};
觉得有用的话可以点点赞,支持一下。
如果愿意的话关注一下。会对你有更多的帮助。
每天都会不定时更新哦 >人< 。
相关文章:

力扣第55题 跳跃游戏 c++ 贪心 + 覆盖 加暴力超时参考
题目 55. 跳跃游戏 中等 相关标签 贪心 数组 动态规划 给你一个非负整数数组 nums ,你最初位于数组的 第一个下标 。数组中的每个元素代表你在该位置可以跳跃的最大长度。 判断你是否能够到达最后一个下标,如果可以,返回 true &…...
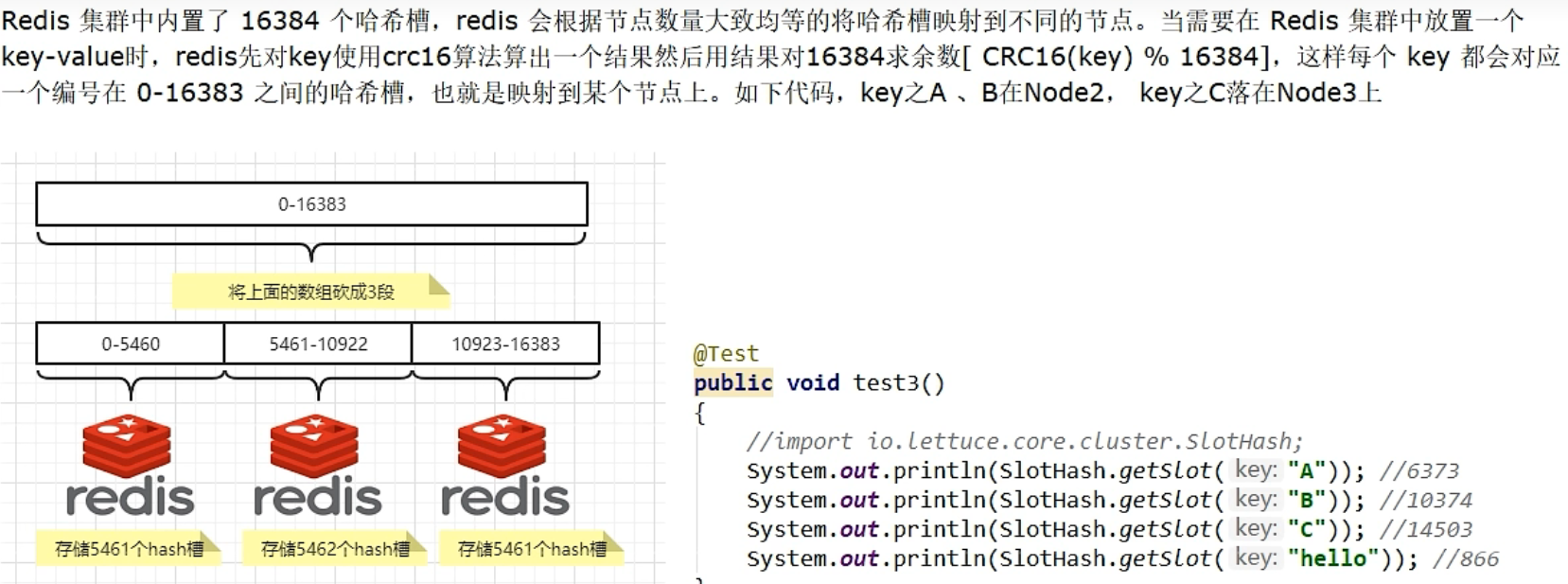
系列十四、Redis的集群(一)
一、是什么 1.1、概述 由于数据量过大,单个master-slave模式难以承担,当出现master节点故障的一瞬间,哨兵重新选举新的master节点之前,这一小段时间将会导致Redis服务不可用,因此需要对多个master-slave主从复制集进行…...

红帽认证 | RHCE考试包括哪些内容?
Red Hat Certified Engineer(RHCE)考试是一项面向企业级系统管理员的认证考试,是认证Linux系统管理员技能的一种方式。 RHCE证书是Linux管理员领域中最受欢迎和最受认可的证书之一。 那RHCE考试都有哪些内容呢,一起来看看吧&…...
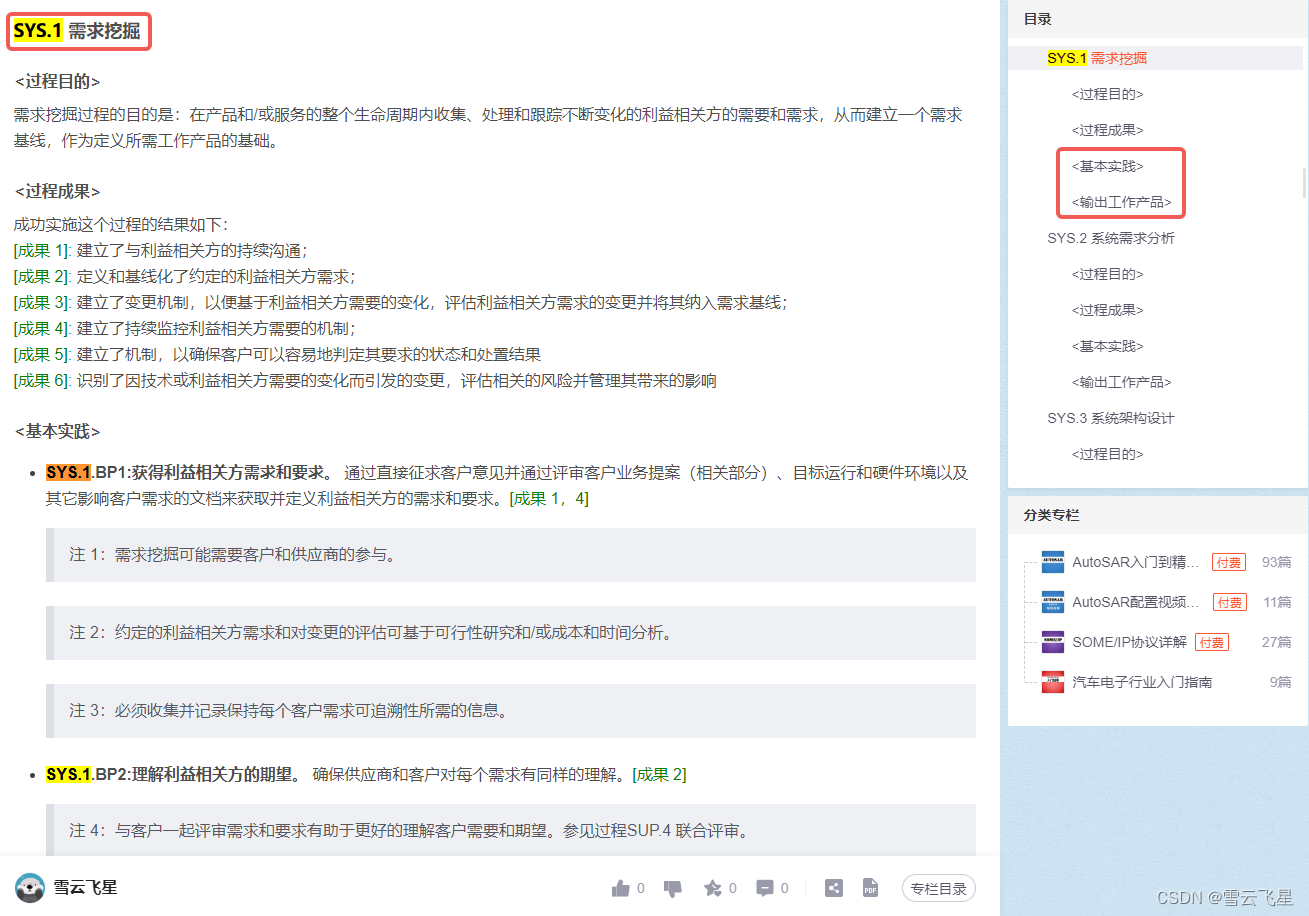
ASPICE标准快速掌握「3.1. 实践示例」
实践示例 本章内容是最重要的,建议慢下来跟着博主的思路一步一步前进 1. 示例背景说明 假设我们现在是一个Tier1的车窗控制软件开发商,我们给OEM提供软件解决方案 1.1. 本过程目标 根据客户、上级部门、安全团队与质量团队等提出的要求,本项目要求SYS.1过程达到ASPICE过…...

pytorch 训练可视化
pytorch 训练可视化 1.from torch.utils.tensorboard 1.from torch.utils.tensorboard from torch.utils.tensorboard import SummaryWriter在最新版本的pytorch中官方提供了tensorboard的api。以下是官方教程的链接 https://pytorch.org/tutorials/intermediate/tensorboard…...

webgis开发参考资料
一、ArcGIS相关 1、ArcGIS for Server 10.3.X 新型紧凑型缓存的解读和应用 http://zhihu.geoscene.cn/article/1038 2、arcgis server 紧促(bundle)格式缓存文件的读取 https://blog.csdn.net/abc553226713/article/details/8668839 3、ArcGIS 10.0紧…...

JSX 注意事项
学习目标: 掌握 JSX 实际开发过程中的一些注意事项 1. JSX 必须具有一个根节点,如果没有根节点可以使用<></>(幽灵节点)代替根节点将所有元素包裹起来 function App() {return (<><div className"App">1</div&…...
)
MQ常见的问题(kafka保证消息不丢失)
MQ常见的问题 1,mq如何避免消息堆积问题。 消息堆积:生产者的生产速率远远大于消费者的消费速率,使消息大批量的堆积在消息队列。 解决方案:1,提升消费者的消费速率(增加消费者集群) 2&…...
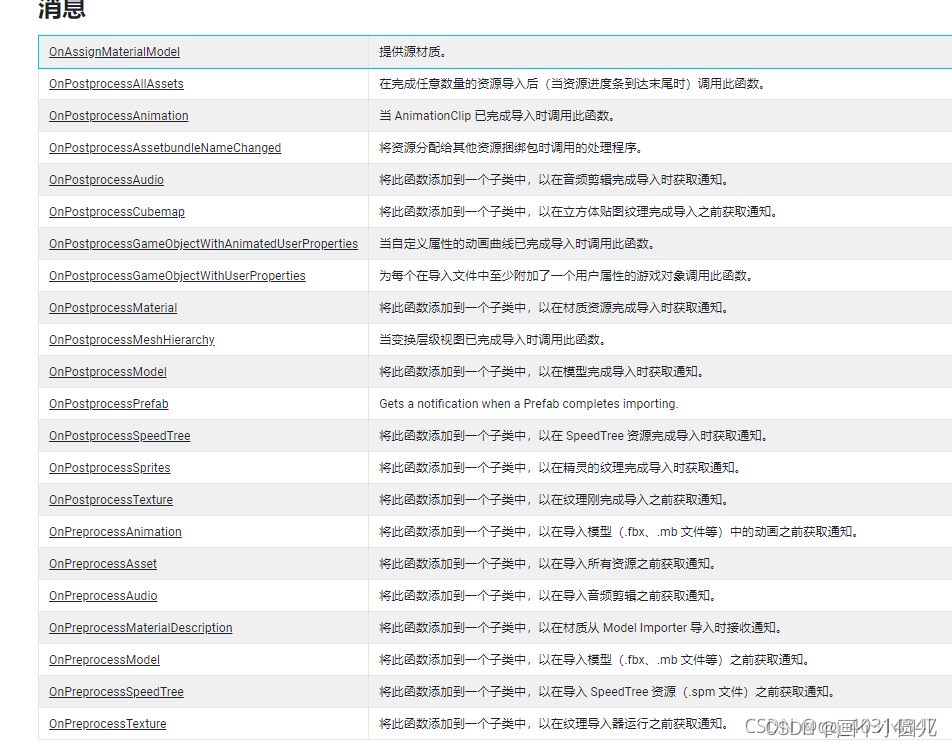
Unity编辑器扩展 --- AssetPostprocessor资源导入自动设置
unity导入资源的编辑器设置: 防止策划资源乱导入,资源导入需要的格式,统一资源管理 AssetPostprocessor资源导入管线 AssetPostprocessor用于在资源导入时自动做一些设置,比如当导入大量图片时,自动设置图片的类型,大小等。Ass…...
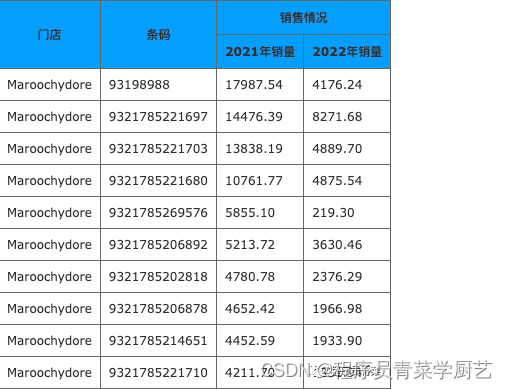
用Flask快速生成报表
一、前言 《用Python快速生成报表之一》 我们介绍了用html-table快速生成表格数据报表,今天我们再介绍一下用Python Flask 快速开发报表,使用的是最古老的套页面方式。 二、Flask快速生成报表 Python有N多Web框架,最强大最出名的是Django&…...

关于时序预测可解释性预测
本文做一些论文收集使用,先更新一两篇 论文 1 Learning Structured Components: Towards Modular and Interpretable Multivariate Time Series Forecasting 论文地址: https://browse.arxiv.org/pdf/2305.13036.pdf 论文代码:https://gi…...
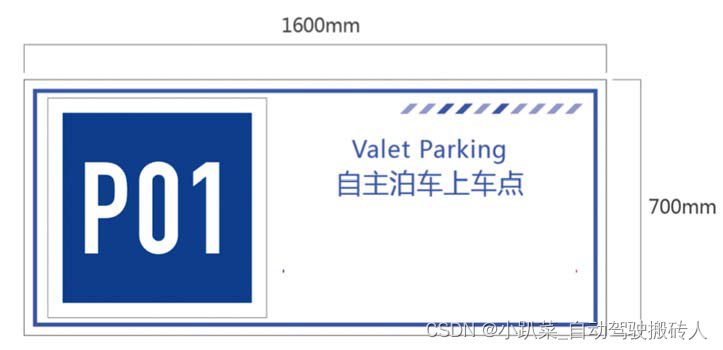
泊车功能专题介绍 ———— AVP系统技术要求之场地规范定位要求
文章目录 停车场场地规范场地分级规范场地标识规范位置标识跨层标识十字路口标识丁字路口处标识闸口/收费口标识上下车点标识 定位功能要求环境要求定位精度要求场端定位要求道路自动驾驶定位要求泊车入位定位要求 车端定位要求道路自动驾驶定位要求泊车入位定位要求初始定位要…...

【STM32】时钟设置函数(寄存器版)
一、STM32时钟设置函数移植 1.时钟模块回顾 一个疑问 前面代码并没有设置时钟为什么可以直接使用。 2.时钟树 3.时钟树分析 1.内部晶振(HSI) 内部晶振不稳定,当我们上电后,会自动产生振动,自动产生时钟,…...

【DDD】贫血模型和充血模型
基于业务开发的项目大多是MVC架构的。成为Web项目的标准开发模式,但它却是违反面向对象编程风格的,是面向过程的。之后基于领域驱动设计开发模式被人提倡。 DDD(Domain-driven design)领域驱动设计是一种通过将实现连接到持续进化…...

【JS学习】字符串的substring方法
1. 介绍 substring 是JavaScript字符串对象的一个方法,用于从一个字符串中提取子字符串,并返回提取的部分。 可以使用 substring 方法来截取字符串的一部分,指定起始索引和结束索引(或只指定起始索引)。 这个方法不…...

vue部署,chunk文件有部分404,解决方案
排查方案: 1,检查项目配置,再vue.config.js里面配置 publicPath: "./",2,打包后检查报错文件是否存在打包目录 3,如果1,2都有 找到部署后404的文件,查看是否为空文件 style里面全注释也会打包文…...
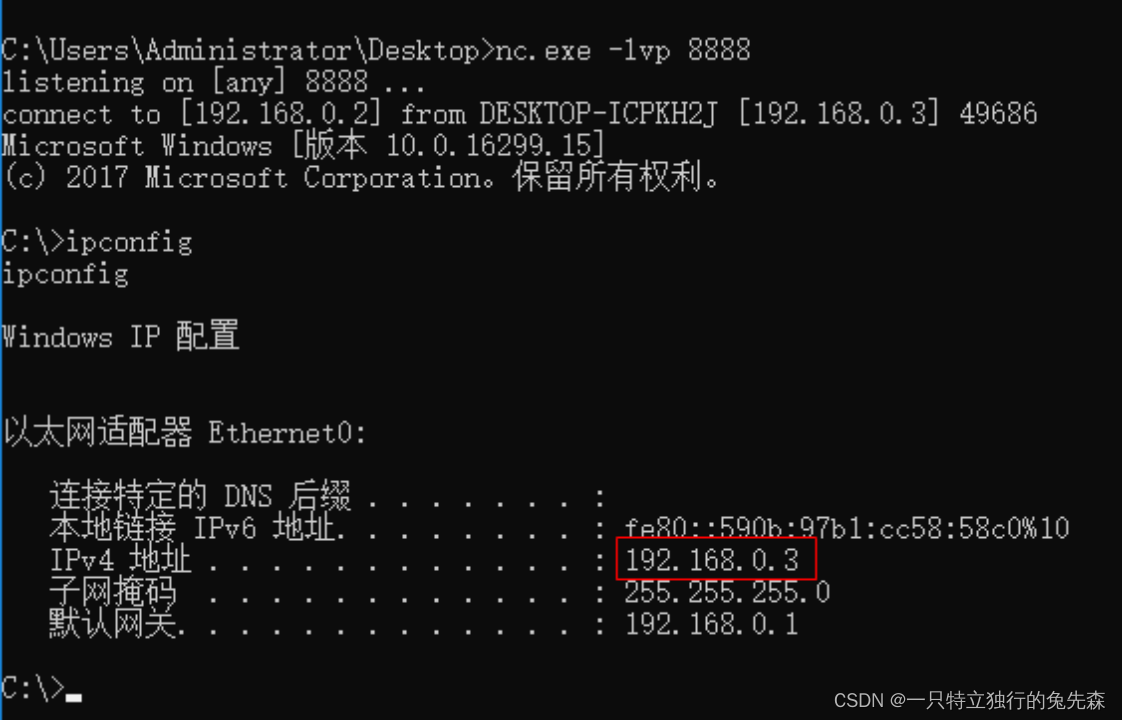
《红蓝攻防对抗实战》六.常规反弹之利用NC在windows系统执行反弹shell
目录 一.利用NC工具在windows系统执行反弹shell 1. Windows正向连接shell 2.Windows反向连接shell 前文推荐: 《红蓝攻防对抗实战》一. 隧道穿透技术详解《红蓝攻防对抗实战》二.内网探测协议出网之TCP/UDP协议探测出网《红蓝攻防对抗实战》三.内网探测协议出网…...
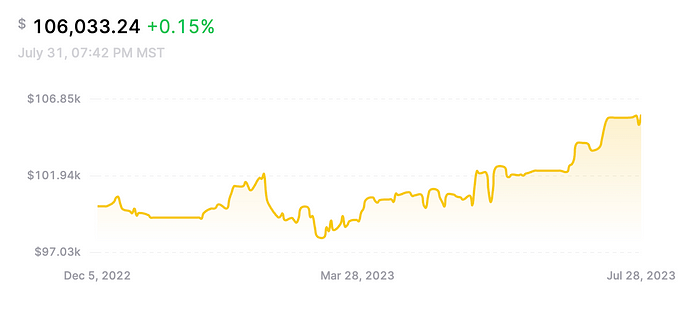
python如何创建自己的对冲交易算法
在这篇文章中,我解释了如何创建一个人工智能来每天为我进行自动交易。 随着机器学习的现代进步和在线数据的轻松访问,参与量化交易变得前所未有的容易。为了让事情变得更好,AWS 等云工具可以轻松地将交易想法转化为真正的、功能齐全的交易机器…...
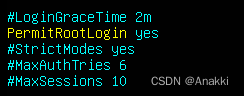
Ubuntu22.04安装,SSH无法连接
Ubuntu初始化安装后,系统默认不允许root通过ssh连接,因此需要完成三个设置 1.修改ssh配置文件 vim /etc/ssh/sshd_config 将PermitRootLogin注释打开,并将值改为yes 保存修改并退出 :wq 2.重启ssh服务 sudo service ssh restart 3.重新打…...

解决dirsearch扫描工具pkg_resources模块警告问题
一、pkg_resources模块问题 ┌──(kali㉿kali)-[~/桌面/XXX/dirsearch-master] └─$ python dirsearch.py -h /home/kali/XX/XXXX/dirsearch-master/dirsearch.py:23: DeprecationWarning: pkg_resources is deprecated as an API. See https://setuptools.pypa.io…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...

Qemu arm操作系统开发环境
使用qemu虚拟arm硬件比较合适。 步骤如下: 安装qemu apt install qemu-system安装aarch64-none-elf-gcc 需要手动下载,下载地址:https://developer.arm.com/-/media/Files/downloads/gnu/13.2.rel1/binrel/arm-gnu-toolchain-13.2.rel1-x…...

【深尚想】TPS54618CQRTERQ1汽车级同步降压转换器电源芯片全面解析
1. 元器件定义与技术特点 TPS54618CQRTERQ1 是德州仪器(TI)推出的一款 汽车级同步降压转换器(DC-DC开关稳压器),属于高性能电源管理芯片。核心特性包括: 输入电压范围:2.95V–6V,输…...

LUA+Reids实现库存秒杀预扣减 记录流水 以及自己的思考
目录 lua脚本 记录流水 记录流水的作用 流水什么时候删除 我们在做库存扣减的时候,显示基于Lua脚本和Redis实现的预扣减 这样可以在秒杀扣减的时候保证操作的原子性和高效性 lua脚本 // ... 已有代码 ...Overridepublic InventoryResponse decrease(Inventor…...
