自然语言处理---RNN、LSTM、GRU模型
RNN模型
RNN模型概述
- RNN(Recurrent Neural Network),中文称作循环神经网络,它一般以序列数据为输入,通过网络内部的结构设计有效捕捉序列之间的关系特征,一般也是以序列形式进行输出。
- RNN的循环机制使模型隐层上一时间步产生的结果,能够作为当下时间步输入的一部分(当下时间步的输入除了正常的输入外还包括上一步的隐层输出)对当下时间步的输出产生影响。
RNN模型的作用
- 因为RNN结构能够很好利用序列之间的关系,因此针对自然界具有连续性的输入序列,如人类的语言,语音等进行很好的处理,广泛应用于NLP领域的各项任务,如文本分类,情感分析,意图识别,机器翻译等。
- 以一个用户意图识别的例子对RNN的运行过程进行简单的分析:
- 第一步:用户输入了"What time is it ?",首先需要对它进行基本的分词,因为RNN是按照顺序工作的,每次只接收一个单词进行处理。
- 第二步:首先将单词"What"输送给RNN,它将产生一个输出O1。
- 第三步:继续将单词"time"输送给RNN,但此时RNN不仅仅利用"time"来产生输出O2,还会使用来自上一层隐层输出O1作为输入信息。
- 第四步:重复这样的步骤,直到处理完所有的单词。
- 第五步:最后将最终的隐层输出O5进行处理来解析用户意图。
RNN模型的分类
- 从两个角度对RNN模型进行分类,第一个角度是输入和输出的结构,第二个角度是RNN的内部构造。
- 按照输入和输出的结构进行分类:
- N vs N - RNN
- N vs 1 - RNN
- 1 vs N - RNN
- N vs M - RNN
- 按照RNN的内部构造进行分类:
- 传统RNN
- LSTM
- Bi-LSTM
- GRU
- Bi-GRU
- N vs N - RNN
- 它是RNN最基础的结构形式,最大的特点就是:输入和输出序列是等长的。由于这个限制的存在,使其适用范围比较小,可用于生成等长度的合辙诗句。
- N vs 1 - RNN
- 有时要处理的问题输入是一个序列,而要求输出是一个单独的值而不是序列,应该怎样建模呢?只要在最后一个隐层输出h上进行线性变换就可以了,大部分情况下,为了更好的明确结果,还要使用sigmoid或者softmax进行处理。这种结构经常被应用在文本分类问题上。
- 1 vs N - RNN
- 如果输入不是序列而输出为序列的情况怎么处理呢?最常采用的一种方式就是使该输入作用于每次的输出之上。这种结构可用于将图片生成文字任务等。
- N vs M - RNN
- 这是一种不限输入输出长度的RNN结构,它由编码器和解码器两部分组成,两者的内部结构都是某类RNN,它也被称为seq2seq架构。输入数据首先通过编码器,最终输出一个隐含变量c,之后最常用的做法是使用这个隐含变量c作用在解码器进行解码的每一步上,以保证输入信息被有效利用。
- seq2seq架构最早被提出应用于机器翻译,因为其输入输出不受限制,如今也是应用最广的RNN模型结构。在机器翻译,阅读理解,文本摘要等众多领域都进行了非常多的应用实践。
传统RNN模型
RNN结构分析

结构解释图
内部结构分析
- 在中间的方块部分,它的输入有两部分,分别是h(t-1)以及x(t),代表上一时间步的隐层输出,以及此时间步的输入,它们进入RNN结构体后,会"融合"到一起,这种融合根据结构解释可知,是将二者进行拼接,形成新的张量[x(t), h(t-1)],之后这个新的张量将通过一个全连接层(线性层),该层使用tanh作为激活函数,最终得到该时间步的输出h(t),它将作为下一个时间步的输入和x(t+1)一起进入结构体。以此类推。
根据结构分析得出内部计算公式:
激活函数tanh的作用:用于帮助调节流经网络的值,tanh函数将值压缩在-1和1之间。
传统RNN优缺点
传统RNN的优势
- 由于内部结构简单,对计算资源要求低,相比RNN变体:LSTM和GRU模型参数总量少了很多,在短序列任务上性能和效果都表现优异。
传统RNN的缺点
- 传统RNN在解决长序列之间的关联时,通过实践,证明经典RNN表现很差,原因是在进行反向传播的时候,过长的序列导致梯度的计算异常,发生梯度消失或爆炸。
梯度消失或爆炸介绍
- 根据反向传播算法和链式法则,梯度的计算可以简化为以下公式
![]()
- 其中sigmoid的导数值域是固定的,在[0, 0.25]之间,而一旦公式中的w也小于1,那么通过这样的公式连乘后,最终的梯度就会变得非常非常小,这种现象称作梯度消失。反之,如果人为的增大w的值,使其大于1,那么连乘够就可能造成梯度过大,称作梯度爆炸。
- 梯度消失或爆炸的危害:
- 如果在训练过程中发生了梯度消失,权重无法被更新,最终导致训练失败;梯度爆炸所带来的梯度过大,大幅度更新网络参数,在极端情况下,结果会溢出(NaN值)。
LSTM模型
LSTM(Long Short-Term Memory)也称长短时记忆结构,它是传统RNN的变体,与经典RNN相比能够有效捕捉长序列之间的语义关联,缓解梯度消失或爆炸现象。同时LSTM的结构更复杂,它的核心结构可以分为四个部分去解析:遗忘门、输入门、细胞状态、输出门。
LSTM结构分析

遗忘门
- 遗忘门部分结构图与计算公式
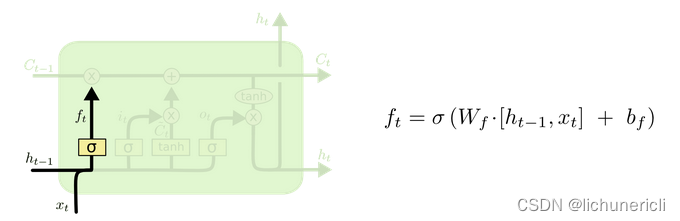
- 遗忘门结构分析
- 与传统RNN的内部结构计算非常相似,首先将当前时间步输入x(t)与上一个时间步隐含状态h(t-1)拼接,得到[x(t), h(t-1)],然后通过一个全连接层做变换,最后通过sigmoid函数进行激活得到f(t)。
- 可以将f(t)看作是门值,好比一扇门开合的大小程度,门值都将作用在通过该扇门的张量,遗忘门门值将作用的上一层的细胞状态上,代表遗忘过去的多少信息, 又因为遗忘门门值是由x(t),h(t-1)计算得来的,因此整个公式意味着根据当前时间步输入和上一个时间步隐含状态h(t-1)来决定遗忘多少上一层的细胞状态所携带的过往信息。
- 激活函数sigmiod的作用:用于帮助调节流经网络的值,sigmoid函数将值压缩在0和1之间。
输入门
- 输入门部分结构图与计算公式

- 输入门结构分析
- 输入门的计算公式有两个,第一个就是产生输入门门值的公式,它和遗忘门公式几乎相同,区别只是在于它们之后要作用的目标上。这个公式意味着输入信息有多少需要进行过滤。输入门的第二个公式是与传统RNN的内部结构计算相同。对于LSTM来讲,它得到的是当前的细胞状态,而不是像经典RNN一样得到的是隐含状态。
细胞状态
- 细胞状态更新图与计算公式

- 细胞状态更新分析
- 细胞更新的结构与计算公式非常容易理解,这里没有全连接层,只是将刚刚得到的遗忘门门值与上一个时间步得到的C(t-1)相乘,再加上输入门门值与当前时间步得到的未更新C(t)相乘的结果。最终得到更新后的C(t)作为下一个时间步输入的一部分。整个细胞状态更新过程就是对遗忘门和输入门的应用。
输出门
- 输出门部分结构图与计算公式

- 输出门结构分析
- 输出门部分的公式也是两个,第一个即是计算输出门的门值,它和遗忘门,输入门计算方式相同。第二个即是使用这个门值产生隐含状态h(t),他将作用在更新后的细胞状态C(t)上,并做tanh激活,最终得到h(t)作为下一时间步输入的一部分。整个输出门的过程,就是为了产生隐含状态h(t)。
Bi-LSTM
Bi-LSTM概述
Bi-LSTM即双向LSTM,它没有改变LSTM本身任何的内部结构,只是将LSTM应用两次且方向不同,再将两次得到的LSTM结果进行拼接作为最终输出。

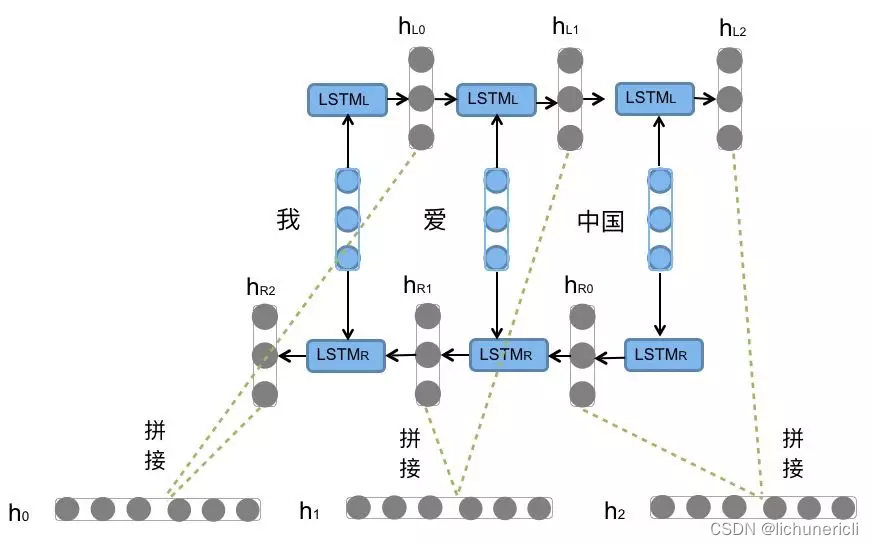
Bi-LSTM结构分析
- 图中对"我爱中国"这句话或者叫这个输入序列,进行了从左到右和从右到左两次LSTM处理,将得到的结果张量进行了拼接作为最终输出。这种结构能够捕捉语言语法中一些特定的前置或后置特征,增强语义关联,但是模型参数和计算复杂度也随之增加了一倍,一般需要对语料和计算资源进行评估后决定是否使用该结构
GRU模型
GRU(Gated Recurrent Unit)也称门控循环单元结构,它也是传统RNN的变体,同LSTM一样能够有效捕捉长序列之间的语义关联,缓解梯度消失或爆炸现象。同时它的结构和计算要比LSTM更简单,它的核心结构可以分为两个部分去解析:更新门、重置门。
GRU结构分析

结构解释图

GRU的更新门和重置门结构图
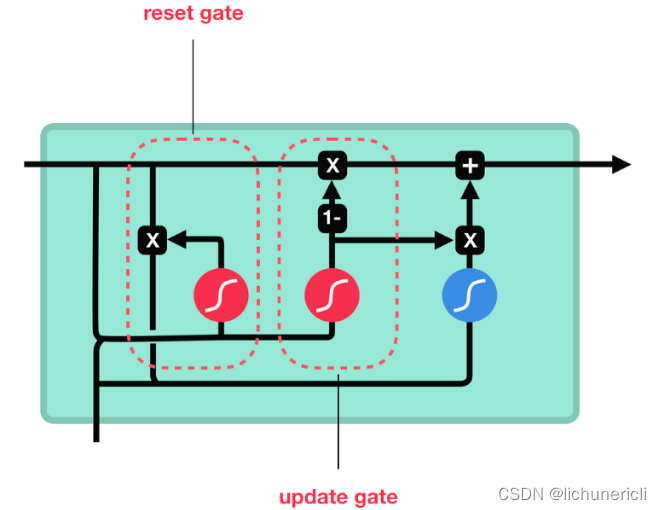
内部结构分析
- 和之前分析过的LSTM中的门控一样,首先计算更新门和重置门的门值,分别是z(t)和r(t),计算方法就是使用X(t)与h(t-1)拼接进行线性变换,再经过sigmoid激活。之后重置门门值作用在了h(t-1)上,代表控制上一时间步传来的信息有多少可以被利用。
- 接着就是使用这个重置后的h(t-1)进行基本的RNN计算,即与x(t)拼接进行线性变化,经过tanh激活,得到新的h(t)。
- 最后更新门的门值会作用在新的h(t),而1-门值会作用在h(t-1)上,随后将两者的结果相加,得到最终的隐含状态输出h(t),这个过程意味着更新门有能力保留之前的结果,当门值趋于1时, 输出就是新的h(t),而当门值趋于0时,输出就是上一时间步的h(t-1)。
Bi-GRU
Bi-GRU与Bi-LSTM的逻辑相同,都是不改变其内部结构,而是将模型应用两次且方向不同,再将两次得到的LSTM结果进行拼接作为最终输出。
GRU优缺点
-
GRU的优势
- GRU和LSTM作用相同,在捕捉长序列语义关联时,能有效抑制梯度消失或爆炸,效果都优于传统RNN且计算复杂度相比LSTM要小。
-
GRU的缺点:
- GRU仍然不能完全解决梯度消失问题,同时其作用RNN的变体,有着RNN结构本身的一大弊端,即不可并行计算,这在数据量和模型体量逐步增大的未来,是RNN发展的关键瓶颈。
相关文章:

自然语言处理---RNN、LSTM、GRU模型
RNN模型 RNN模型概述 RNN(Recurrent Neural Network),中文称作循环神经网络,它一般以序列数据为输入,通过网络内部的结构设计有效捕捉序列之间的关系特征,一般也是以序列形式进行输出。RNN的循环机制使模型隐层上一时间步产生的…...
rust学习——方法 Method
文章目录 方法 Method定义方法self、&self 和 &mut self方法名跟结构体字段名相同 带有多个参数的方法关联函数多个 impl 定义为枚举实现方法 rust 结构体与枚举的区别回答1回答2 方法 Method 从面向对象语言过来的同学对于方法肯定不陌生,class 里面就充斥…...
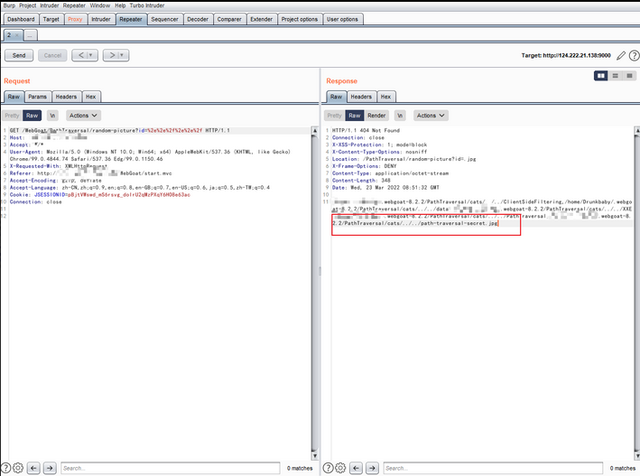
目录遍历漏洞
漏洞挖掘之目录遍历漏洞 (baidu.com) 从0到1完全掌握目录遍历漏洞 0x01 什么是目录遍历漏洞 目录遍历漏洞是由于网站存在配置缺陷,导致网站目录可以被任意浏览,这会导致网站很多隐私文件与目录泄露。 比如数据库备份文件、配置文件等,攻击…...

Python基础入门例程10-NP10 牛牛最好的朋友们
目录 描述 输入描述: 输出描述: 示例1 解答: 说明: 描述 牛牛有两个最好的朋友,他们的名字分别用input读入记录在两个字符串中,请使用字符串连接()帮助牛牛将两个朋友的名字依…...
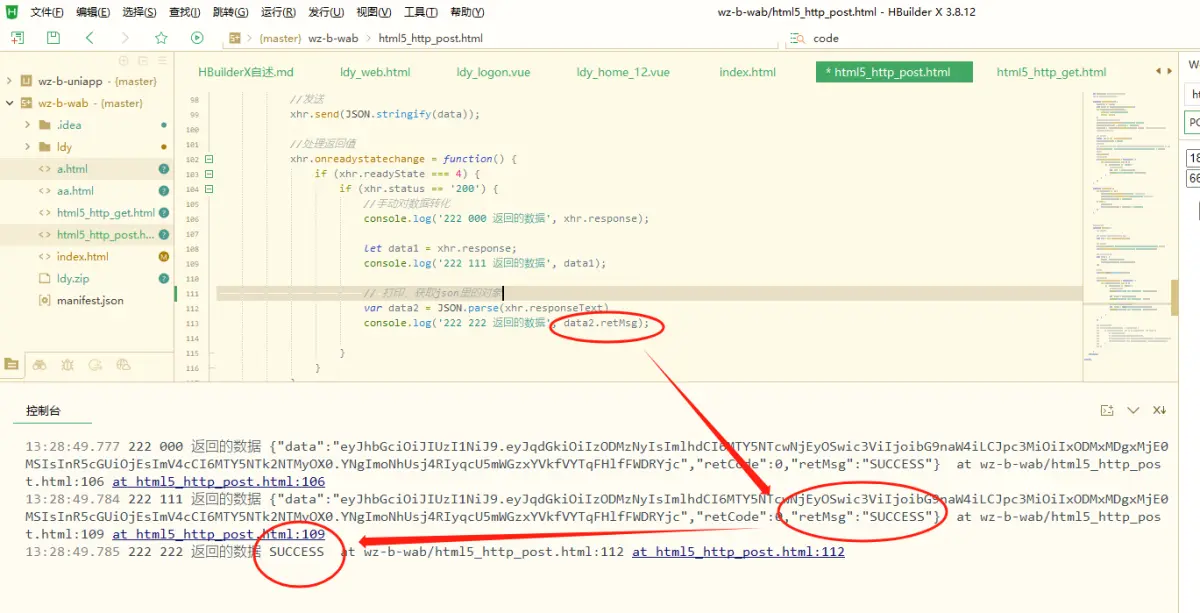
html web前端,登录,post请求提交 json带参
html web前端,登录,post请求提交 json带参 3ca9855b3fd279fa17d46f01dc652030.jpg <!DOCTYPE html> <html><head><meta http-equiv"Content-Type" content"text/html; charsetutf-8" /><title></t…...

防火墙实验
防火墙 ping(网络测试工具,测试主机之间的可达性)原理: 发送一些小的网络数据包(ICMP数据包)到目标主机,并等待目标主机返回一个响应(通常是回显应答 Echo Reply)。 ss…...

php中进程、线程、协程详细讲解
目录 一、什么是进程、线程、协程 1、什么是进程(Process): 2 、什么是线程(Thread): 3、什么是协程(Coroutine): 二、 进程、线程、协程的关系 1、进程与线程关系 …...

无线通信中SINR的含义
在无线通信中,SINR代表"Signal-to-Interference-plus-Noise Ratio",即信号与干扰加噪声比。这是一个重要的性能度量,用于评估和描述接收信号的质量,以及在无线通信系统中的通信性能。 SINR考虑了以下三个关键因素&…...

pnp单目相机标定测距
参考:opencv 单目相机pnp测距(Cpp)-CSDN博客...
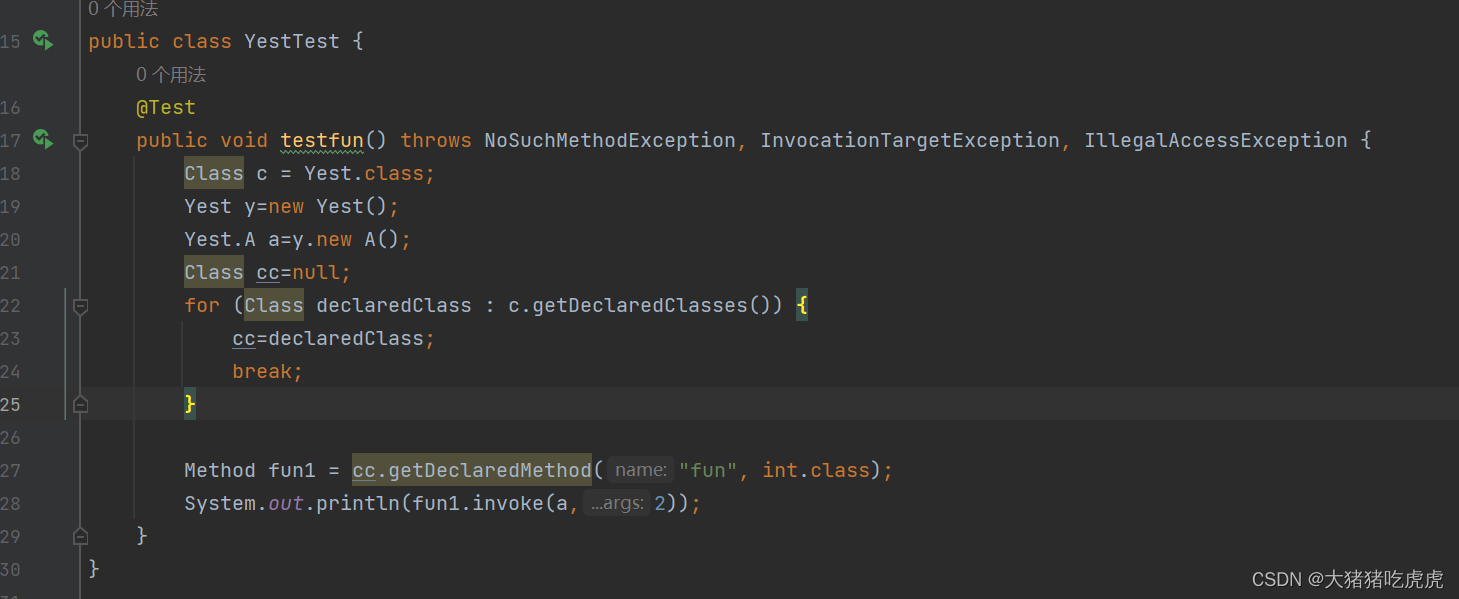
Java反射获取内部类方法
Java反射获取内部类方法 结论一、案例准备二、测试方法:使用反射获取类的成员内部类和方法具体操作具体操作(使用getDeclaredClasses) 结论 Java 通过反射可以获得内部类,包括内部类属性信息和方法。 一、案例准备 创建了一个类…...

发挥服务器的无限潜能:创意项目、在线社区和更多
✅作者简介:2022年博客新星 第八。热爱国学的Java后端开发者,修心和技术同步精进。 🍎个人主页:Java Fans的博客 🍊个人信条:不迁怒,不贰过。小知识,大智慧。 ✨特色专栏:…...
【java】A卷+B卷)
华为OD 绘图机器(100分)【java】A卷+B卷
华为OD统一考试A卷+B卷 新题库说明 你收到的链接上面会标注A卷还是B卷。目前大部分收到的都是B卷。 B卷对应20022部分考题以及新出的题目,A卷对应的是新出的题目。 我将持续更新最新题目 获取更多免费题目可前往夸克网盘下载,请点击以下链接进入: 我用夸克网盘分享了「华为O…...

文件上传接口
以下是一个简单的Java文件上传接口的示例代码: import org.springframework.http.HttpStatus;import org.springframework.http.ResponseEntity;import org.springframework.web.bind.annotation.PostMapping;import org.springframework.web.bind.annotation.Requ…...

基于矢量控制策略的异步电机调速系统设计
摘 要 由于国内人民生活水平的提高,科技不断地进步,控制不断地完善,从而促使矢量控制技术在电气传动系统领域占据主导权,也使得交流异步电机调速控制系统被广泛应用。在交流异步电机调速系统设计领域中,矢量控制成为目…...

Ubuntu下载工具ip addr、ifconfig、ping、make
Ubuntu下载工具ip addr、ifconfig、ping、make ping 在 Ubuntu 上获取网络工具包通常是通过安装相关软件包的方式来完成的。Ubuntu 默认包含一些常见的网络工具,但如果你需要安装其他工具,你可以使用 apt 命令或者 snap 命令进行安装。以下是一些常见的…...

【数据结构】常见复杂度习题详解 ------ 习题篇
文章目录 📋前言一. ⛳️前篇回顾二. ⛳️常见时间复杂度计算举例1️⃣实例一2️⃣实例二3️⃣实例三4️⃣实例四5️⃣实例五6️⃣实例六7️⃣实例七8️⃣实例八 三. ⛳️常见空间复杂度计算举例1️⃣实例一2️⃣实例二3️⃣实例三 四. ⛳️总结 📋前言 …...

一、vue介绍
一、介绍 vue式前端框架,是一套用于构建用户界面的渐进式框架 1、安装vue 安装node.js(配置环境变量) https://nodejs.org/en/download/ 更换镜像 npm config set registry https://registry.npm.taobao.org 查看镜像 npm config get regi…...

Linux ARMv8 异常向量表
http://blog.chinaunix.net/uid-69947851-id-5830546.html 本章接着《Linux内核启动》部分讲解,我们知道了在进入start_kernel之前,通过指令adr_l x8, vectors;msr vbar_el1, x8设置了异常向量表,那么异常向量表的结构是怎么样…...

C++基类和派生类的内存分配,多态的实现
目录 基类和派生类的内存分配基类和派生类的成员归属多态的实现 基类和派生类的内存分配 类包括成员变量(data member)和成员函数(member function)。 成员变量分为静态数据(static data)和非静态数据&…...

C/C++基础
C 二进制 问题:二进制怎么表示整数、小数、正数、负数,如何存储?加减乘除怎么运算(见文章《计算机加减乘除本质》)? 变量 c定义一个变量的时候,需要事先定义变量大小和变量类型。 //有符号…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...

