【学习笔记】CF1784F Minimums or Medians
首先让 n n n乘上 2 2 2。
考虑枚举最终被删除的位置有哪些。 a i = 0 a_i=0 ai=0表示这个位置被删除, a i = 1 a_i=1 ai=1表示这个位置被保留,设满足 a i = 0 a_i=0 ai=0的前缀长度为 l l l( l l l是偶数), p r e i pre_i prei表示 a i a_i ai的前缀和,则从左往右对于每个极长的被删除的连续段 [ l , r ] [l,r] [l,r],其能够被删除的充要条件是:
- r − l + 1 r-l+1 r−l+1是偶数
- p r e r ≤ n − r ≤ p r e r + c n t pre_r\le n-r\le pre_r+cnt prer≤n−r≤prer+cnt
注意到式子满足单调性,因此我们只用判断除了前缀外的第一个连续段是否满足上界,以及最后一个连续段是否满足下界。
对于最后一个连续段,注意到 p r e r + n − r = n − 2 K pre_r+n-r=n-2K prer+n−r=n−2K,因此可以等价变形成 n − r ≥ n 2 − K n-r\ge \frac{n}{2}-K n−r≥2n−K,即 r ≤ n 2 + K r\le \frac{n}{2}+K r≤2n+K。这其实从另一个角度更好理解:第 i i i次操作删除的数不会超过 n 2 + i \frac{n}{2}+i 2n+i(见Alex_Wei的题解)。因此,对于 n 2 + K \frac{n}{2}+K 2n+K之后的数一定都是保留的,不会影响答案。
对于第一个连续段,发现 p r e r + c n t = l − 1 pre_r+cnt=l-1 prer+cnt=l−1,因此枚举 l l l,得到 r ≥ n − l + 1 r\ge n-l+1 r≥n−l+1,因此 [ l , n − l + 1 ] [l,n-l+1] [l,n−l+1]全部被删除,而 [ n − l + 2 , n 2 + K ] [n-l+2,\frac{n}{2}+K] [n−l+2,2n+K]只需满足连续段长度为偶数即可。
最后,我们注意到从 n n n个数中选 2 k 2k 2k个数,使得每一段为偶数的方案数为 ( n − k k ) \binom{n-k}{k} (kn−k),因此枚举 c n t , l cnt,l cnt,l后计算组合数:
- 若 l ≤ n 2 l\le \frac{n}{2} l≤2n,则:
∑ c n t ≤ K ∑ max ( 2 c n t + 2 , n 2 − K + 1 ) ≤ l ≤ n 2 f ( K + l − n 2 − 1 , K − c n t − n 2 + l − 1 ) \sum_{cnt\le K}\sum_{\max(2cnt+2,\frac{n}{2}-K+1)\le l\le \frac{n}{2}}f(K+l-\frac{n}{2}-1,K-cnt-\frac{n}{2}+l-1) cnt≤K∑max(2cnt+2,2n−K+1)≤l≤2n∑f(K+l−2n−1,K−cnt−2n+l−1)
其中 f ( n , m ) = ( n − m m ) f(n,m)=\binom{n-m}{m} f(n,m)=(mn−m)。
- 若 l > n 2 l>\frac{n}{2} l>2n,则:
∑ c n t ≤ K f ( n 2 + K − max ( 2 c n t + 1 , n 2 ) , K − c n t ) \sum_{cnt\le K}f(\frac{n}{2}+K-\max(2cnt+1,\frac{n}{2}),K-cnt) cnt≤K∑f(2n+K−max(2cnt+1,2n),K−cnt)
对于第二部分,可以 O ( n ) O(n) O(n)计算;对于第一部分,利用 ( i + 1 j ) = ( i j ) + ( i j − 1 ) \binom{i+1}{j}=\binom{i}{j}+\binom{i}{j-1} (ji+1)=(ji)+(j−1i)可以转化为求上指标减少 1 1 1时的答案,而下指标的指针移动是 O ( 1 ) O(1) O(1)的,因此总复杂度 O ( n ) O(n) O(n)。
#include<bits/stdc++.h>
#define ll long long
#define pb push_back
#define fi first
#define se second
#define db double
#define inf 0x3f3f3f3f
using namespace std;
const int mod=998244353;
const int N=2e6+5;
ll fac[N],res,sm,ifac[N];
int n,K;
ll fpow(ll x,ll y=mod-2){ll z(1);for(;y;y>>=1){if(y&1)z=z*x%mod;x=x*x%mod;}return z;
}
void init(int n){fac[0]=1;for(int i=1;i<=n;i++)fac[i]=fac[i-1]*i%mod;ifac[n]=fpow(fac[n]);for(int i=n;i>=1;i--)ifac[i-1]=ifac[i]*i%mod;
}
ll binom(int x,int y){if(x<0||y<0||x<y)return 0;return fac[x]*ifac[y]%mod*ifac[x-y]%mod;
}
void add(ll &x,ll y){x=(x+y)%mod;
}
ll f(int n,int m){if(n<0||m<0||n<2*m)return 0;return binom(n-m,m);
}
int l,r;
int main(){ios::sync_with_stdio(false);cin.tie(0),cout.tie(0);cin>>n>>K,n<<=1,init(n);if(K==0||n/2==K){cout<<1;return 0;}l=0,r=K-1,res=1,sm=1;for(int i=1;i<=K;i++){int nl=K-i-n/2+max(2*i+2,n/2-K+1)-1,nr=K-i-1;if(nl<=nr){while(l>nl)add(sm,binom(i-1,--l));while(r<nr)add(sm,binom(i-1,++r));while(l<nl)add(sm,-binom(i-1,l++));while(r>nr)add(sm,-binom(i-1,r--));add(sm,sm),add(sm,binom(i-1,nl-1)),add(sm,-binom(i-1,nr));add(res,sm);}add(res,f(n/2+K-max(2*i+1,n/2),K-i));}cout<<(res+mod)%mod;
}
相关文章:

【学习笔记】CF1784F Minimums or Medians
首先让 n n n乘上 2 2 2。 考虑枚举最终被删除的位置有哪些。 a i 0 a_i0 ai0表示这个位置被删除, a i 1 a_i1 ai1表示这个位置被保留,设满足 a i 0 a_i0 ai0的前缀长度为 l l l( l l l是偶数), p r e i pre…...

如何系列 如何玩转远程调用之OpenFegin+SpringBoot(非Cloud)
文章目录 简介原生Fegin示例基础契约日志重试编码器/解码器自定义解码器 请求拦截器响应拦截器表单文件上传支持错误解码器断路器指标metrics客户端 配合SpringBoot(阶段一)配合SpringBoot(阶段二)1.EnableLakerFeignClients2.Lak…...
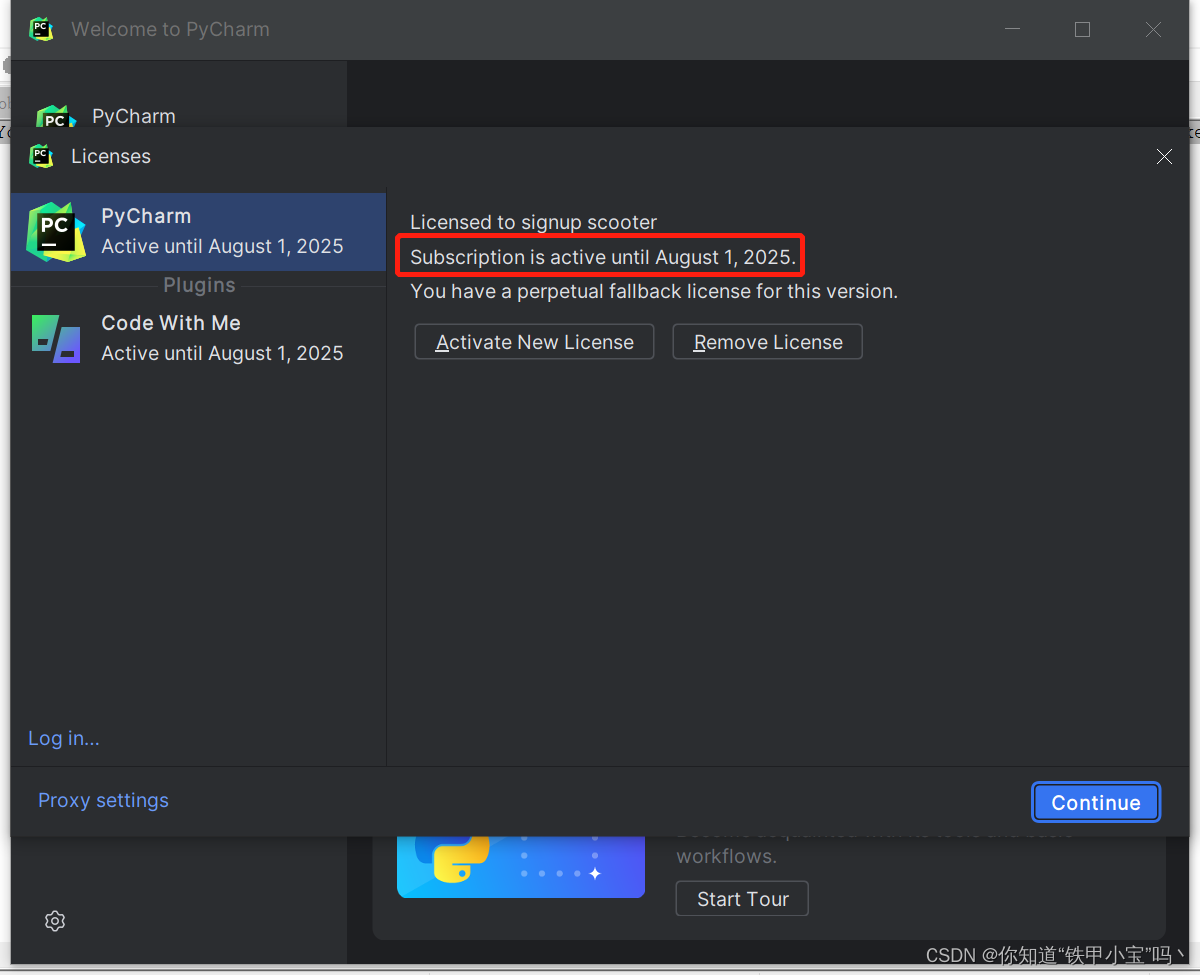
Python学习第2天-安装pycharm
文章目录 前言一、下载二、安装1.选择安装目录2.安装配置 总结 前言 好用的工具可以极大地提高生产力,开发Python推荐使用jetbrains全家桶的pycharm。 一、下载 通过官网下载安装包。 二、安装 1.选择安装目录 2.安装配置 一路Next,安装完成 总结 …...

等电位连接器行业应用综合方案
等电位连接器的原理 等电位连接器的原理是利用气体放电管或压敏电阻等非线性元件,当连接器两端的电位差大于所限峰值电压时,连接器导通,迫使连接器两端不同接地体电位基本相等,消除接地体间放电现象,从而避免了由于地…...

内裤洗衣机有用吗?最好用的四款内衣洗衣机测评
相信很多小伙伴往往会因为懒而不想洗内衣,又或者洗内衣时经常会洗不干净!这时就很有必要入手一台内衣洗衣机了,当我们洗完澡时,顺手把内衣放入洗衣机内,一键启动即可把我们的内衣洗得干干净净!同时还可以为…...
足底筋膜炎能自愈吗
什么是足底筋膜炎 足底筋膜炎是足底的肌腱或者筋膜发生无菌性炎症所致。最常见症状是脚跟的疼痛与不适,压痛点常在足底近足跟处,有时压痛较剧烈,且持续存在。晨起时疼痛感觉明显,行走过度时疼痛感加剧,严重患者甚至站…...

牛客网刷题-(3)
🌈write in front🌈 🧸大家好,我是Aileen🧸.希望你看完之后,能对你有所帮助,不足请指正!共同学习交流. 🆔本文由Aileen_0v0🧸 原创 CSDN首发🐒 如…...

Centos7 安装 Etcd
Github上下载并解压安装包 wget https://github.com/coreos/etcd/releases/download/v3.4.10/etcd-v3.4.10-linux-amd64.tar.gz tar xzvf etcd-v3.4.10-linux-amd64.tar.gz mv etcd-v3.4.10-linux-amd64 /opt/etcd解压后是一些文档和两个二进制文件etcd和etcdctl。etcd是serve…...
powerjob基于springboot2.1.6.RELEASE版本的问题研究
项目背景:基于第三代框架的集成问题,如果对于powerjob不熟悉的朋友,可以参考官方文档PowerJob 简介 语雀 关于语雀 23 日故障的公告 (qq.com) 简单插一句,针对语雀文档故障的心得,数据恢复,完整性&#…...

【AI视野·今日CV 计算机视觉论文速览 第270期】Wed, 18 Oct 2023
AI视野今日CS.CV 计算机视觉论文速览 Wed, 18 Oct 2023 Totally 60 papers 👉上期速览✈更多精彩请移步主页 Daily Computer Vision Papers 4K4D: Real-Time 4D View Synthesis at 4K Resolution Authors Zhen Xu, Sida Peng, Haotong Lin, Guangzhao He, Jiaming …...
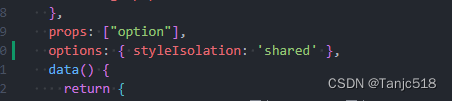
uni-app小程序,uview-ui组件样式无法穿透修改的解决办法
1.首先设置以下选项.该选项的作用是让微信小程序允许样式穿透. 在需要改动的文件内加上 options: { styleIsolation: shared } 2.然后再使用vue的样式穿透写法. ::v-deep .类样式{} 或者 /deep/ .类样式{}...

Codeforces Round 515
Portal. C. Books Queries Portal. sol. D. Boxes Packing Portal. 把从左至右删物品转化为从右至左加物品。模拟即可。 #include <bits/stdc.h> using namespace std;const int maxn2e55; int a[maxn];int main() {int n,m,k;cin>>n>>m>>k;for(…...
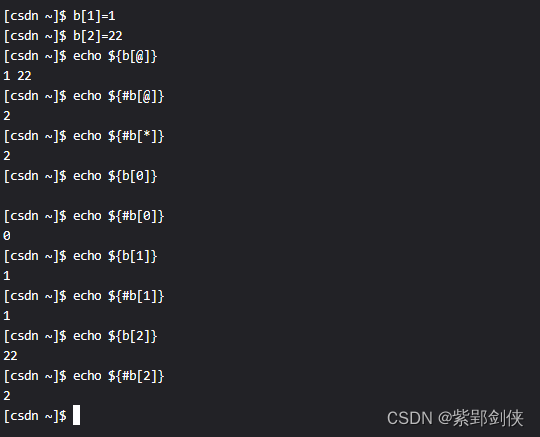
Linux shell编程学习笔记15:定义数组、获取数组元素值和长度
一、 Linux shell 脚本编程中的数组概述 数组是一种常见的数据结构。跟大多数编程语言一样,大多数Linux shell脚本支持数组,但对数组的支持程度各不相同,比如数组的维度,是支持一维数组还是多维数组?再如,…...

k8s部署kafka,并使用zookeeper做注册中心
kafka在3.x版本后增加KRaft作为自己的注册中心,可以不依赖外部的zk;这里上一篇已经部署好了zk,kafka依然使用zk作为注册中心。 这里使用kafka是为集成zipkin收发微服务接口链路日志数据,只需要部署1个实列即可够用。 编写脚本yam…...

关于Nginx缓存
Nginx缓存 一般情况下系统用到的缓存有三种 服务端缓存: 缓存存在后端服务器,如redis代理缓存: 缓存存储在代理服务器或中间件,内容从后端服务器获取,保存在本地客户端缓存: 缓存在浏览器什么时候会出现3…...

为什么Open3D可视化TensorFlow张量速度超慢
问题描述 在使用Open3D可视化TensorFlow张量表示的点云时速度超慢 原因分析 可能是因为Open3D没有针对tf.Tensor做优化,也可能是tf.Tensor本身没有对张量的操作做优化,所以可能如果要在CPU中计算,numpy可能性能更好。 解决方案 open3d.u…...
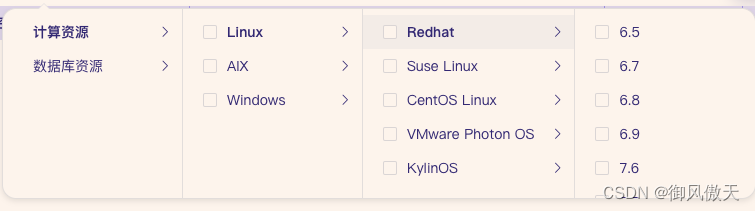
使用element-UI Cascader组件,实现第一级单选选,第二级,第三级,子级可以多选
最近开发过程中,遇到需求测一个需求,就是级联选择器,需要多选;但是第一级是单选; 既要单选又要复选。参照网上内容,自己整理了一下功能实现; 如下图: 思路:1.把第一层的…...
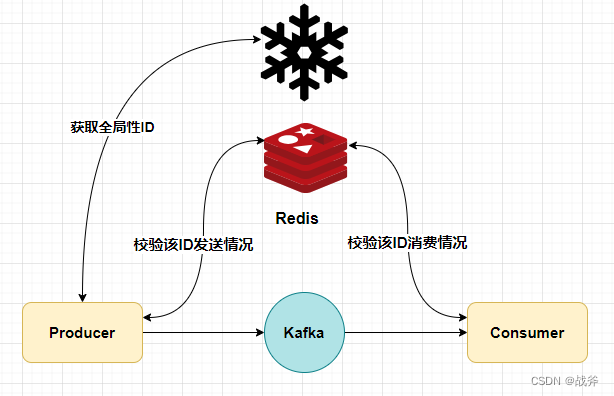
防止消息丢失与消息重复——Kafka可靠性分析及优化实践
系列文章目录 上手第一关,手把手教你安装kafka与可视化工具kafka-eagle Kafka是什么,以及如何使用SpringBoot对接Kafka 架构必备能力——kafka的选型对比及应用场景 Kafka存取原理与实现分析,打破面试难关 防止消息丢失与消息重复——Kafka可…...
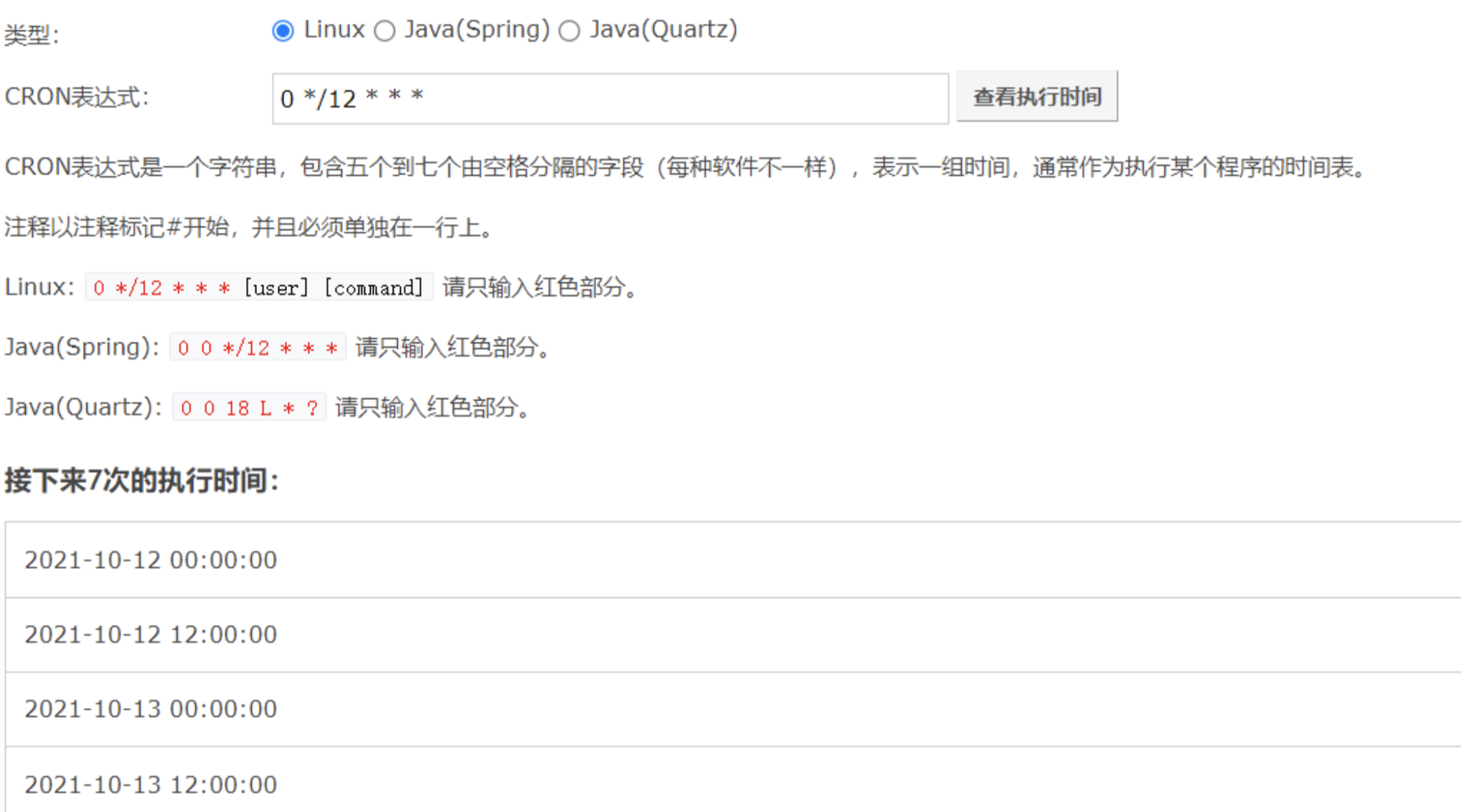
【Linux】Linux中Crontab(定时任务)命令详解及使用教程
文章目录 前言1.使用yum命令安装Crontab:2.查看Crontab状态:3.添加定时任务:4.查看任务列表:5.Crontab相关命令:6.部分脚本无法执行问题:7.Crontab默认调度任务:8.注意清理系统用户的邮件日志&a…...
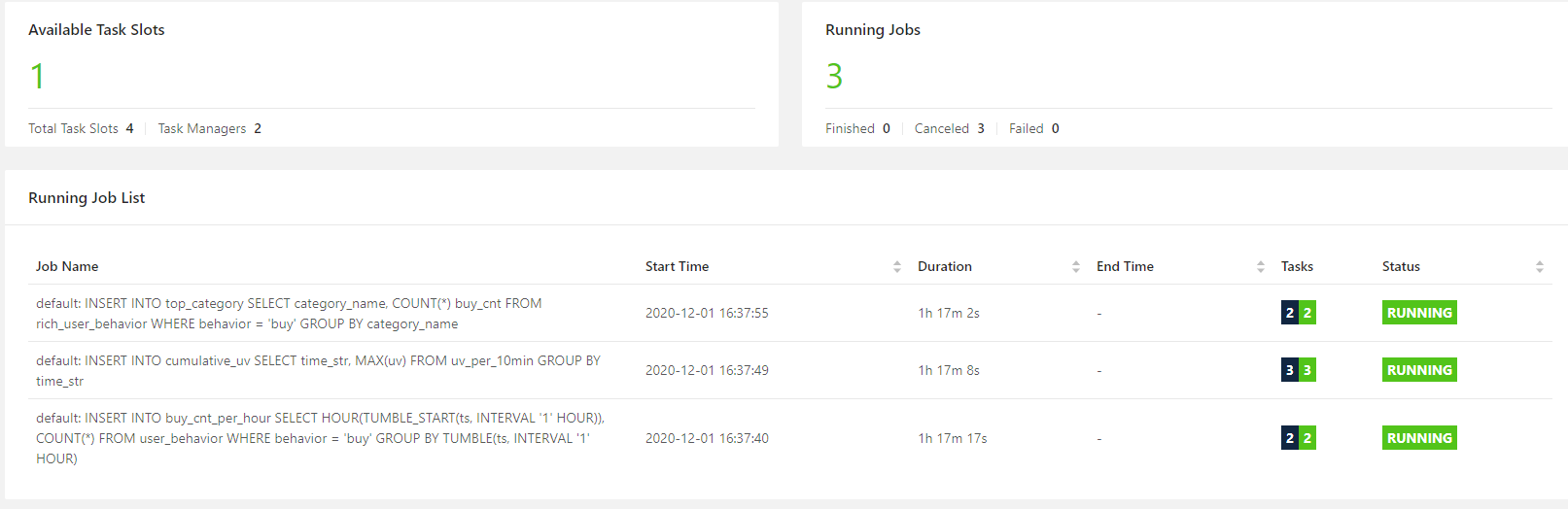
计算机毕设 flink大数据淘宝用户行为数据实时分析与可视化
文章目录 0 前言1、环境准备1.1 flink 下载相关 jar 包1.2 生成 kafka 数据1.3 开发前的三个小 tip 2、flink-sql 客户端编写运行 sql2.1 创建 kafka 数据源表2.2 指标统计:每小时成交量2.2.1 创建 es 结果表, 存放每小时的成交量2.2.2 执行 sql &#x…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...
