数据结构与算法(十):动态规划与贪心算法
参考引用
- Hello 算法
- Github:hello-algo
1. 动态规划算法
- 动态规划将一个问题分解为一系列更小的子问题,并通过存储子问题的解来避免重复计算,从而大幅提升时间效率
问题:给定一个共有 n 阶的楼梯,你每步可以上 1 阶或者 2 阶,请问有多少种方案可以爬到楼顶?
- 下图所示,对于一个 3 阶楼梯,共有 3 种方案可以爬到楼顶

- 本题的目标是求解方案数量,可以考虑通过回溯来穷举所有可能性。具体来说,将爬楼梯想象为一个多轮选择的过程:从地面出发,每轮选择上 1 阶或 2 阶,每当到达楼梯顶部时就将方案数量加 1,当越过楼梯顶部时就将其剪枝
/* 回溯 */ void backtrack(vector<int> &choices, int state, int n, vector<int> &res) {// 当爬到第 n 阶时,方案数量加 1if (state == n)res[0]++;// 遍历所有选择for (auto &choice : choices) {// 剪枝:不允许越过第 n 阶if (state + choice > n)break;// 尝试:做出选择,更新状态backtrack(choices, state + choice, n, res);// 回退} }/* 爬楼梯:回溯 */ int climbingStairsBacktrack(int n) {vector<int> choices = {1, 2}; // 可选择向上爬 1 或 2 阶int state = 0; // 从第 0 阶开始爬vector<int> res = {0}; // 使用 res[0] 记录方案数量backtrack(choices, state, n, res);return res[0]; }
1.1 方法一:暴力搜索
- 回溯算法通常并不显式地对问题进行拆解,而是将问题看作一系列决策步骤,通过试探和剪枝,搜索所有可能的解。可以尝试从问题分解的角度分析这道题。设爬到第 i i i 阶共有 d p [ i ] dp[i] dp[i] 种方案,那么 d p [ i ] dp[i] dp[i] 就是原问题,其子问题包括
d p [ i − 1 ] , d p [ i − 2 ] , … , d p [ 2 ] , d p [ 1 ] dp[i-1],dp[i-2],\ldots,dp[2],dp[1] dp[i−1],dp[i−2],…,dp[2],dp[1]
- 由于每轮只能上 1 阶或 2 阶,因此当站在第 i 阶楼梯上时,上一轮只可能站在第 i-1 阶或第 i-2 阶上。换句话说,只能从第 i-1 阶或第 i-2 阶前往第 i 阶
- 由此便可得出一个重要推论:爬到第 i-1 阶的方案数加上爬到第 i-2 阶的方案数就等于爬到第 i 阶的方案数
- 在爬楼梯问题中,各子问题之间存在递推关系,原问题的解可以由子问题的解构建得来,下图展示了该递推关系
d p [ i ] = d p [ i − 1 ] + d p [ i − 2 ] dp[i]=dp[i-1]+dp[i-2] dp[i]=dp[i−1]+dp[i−2]

- 可以根据递推公式得到暴力搜索解法
- 以 d p [ n ] dp[n] dp[n] 为起始点,递归地将一个较大问题拆解为两个较小问题的和,直至到达最小子问题 d p [ 1 ] dp[1] dp[1] 和 d p [ 2 ] dp[2] dp[2] 时返回。其中,最小子问题的解是已知的,即 d p [ 1 ] = 1 dp[1]=1 dp[1]=1、 d p [ 2 ] = 2 dp[2] = 2 dp[2]=2,表示爬到第 1、2 阶分别有 1、2 种方案
/* 搜索 */ int dfs(int i) {// 已知 dp[1] 和 dp[2] ,返回之if (i == 1 || i == 2)return i;// dp[i] = dp[i-1] + dp[i-2]int count = dfs(i - 1) + dfs(i - 2);return count; }/* 爬楼梯:搜索 */ int climbingStairsDFS(int n) {return dfs(n); } - 下图展示了暴力搜索形成的递归树。对于问题 d p [ n ] dp[n] dp[n],其递归树的深度为 n,时间复杂度为 O ( 2 n ) O(2^n) O(2n)
- 指数阶属于爆炸式增长,如果输入一个比较大的 n,则会陷入漫长的等待之中
- 指数阶的时间复杂度是由于 “重叠子问题” 导致的,以此类推,子问题中包含更小的重叠子问题,子子孙孙无穷尽也,绝大部分计算资源都浪费在这些重叠的问题上

1.2 方法二:记忆化搜索
- 为了提升算法效率,希望所有的重叠子问题都只被计算一次。为此,声明一个数组 mem 来记录每个子问题的解,并在搜索过程中将重叠子问题剪枝
- 当首次计算 d p [ i ] dp[i] dp[i] 时,将其记录至 mem[i],以便之后使用
- 当再次需要计算 d p [ i ] dp[i] dp[i] 时,便可直接从 mem[i] 中获取结果,从而避免重复计算该子问题
/* 记忆化搜索 */ int dfs(int i, vector<int> &mem) {// 已知 dp[1] 和 dp[2] ,返回之if (i == 1 || i == 2)return i;// 若存在记录 dp[i] ,则直接返回之if (mem[i] != -1)return mem[i];// dp[i] = dp[i-1] + dp[i-2]int count = dfs(i - 1, mem) + dfs(i - 2, mem);// 记录 dp[i]mem[i] = count;return count; }/* 爬楼梯:记忆化搜索 */ int climbingStairsDFSMem(int n) {// mem[i] 记录爬到第 i 阶的方案总数,-1 代表无记录vector<int> mem(n + 1, -1);return dfs(n, mem); } - 下图所示,经过记忆化处理后,所有重叠子问题都只需被计算一次,时间复杂度被优化至 O(n)
- 记忆化搜索是一种 “从顶至底” 的方法,从原问题(根节点)开始,递归地将较大子问题分解为较小子问题,直至解已知的最小子问题(叶节点)。之后,通过回溯将子问题的解逐层收集,构建出原问题的解

1.3 方法三:动态规划
- 动态规划是一种 “从底至顶” 的方法:从最小子问题的解开始,迭代地构建更大子问题的解,直至得到原问题的解
- 由于动态规划不包含回溯过程,因此只需使用循环迭代实现,无须使用递归。在以下代码中,初始化一个数组 dp 来存储子问题的解
/* 爬楼梯:动态规划 */ int climbingStairsDP(int n) {if (n == 1 || n == 2)return n;// 初始化 dp 表,用于存储子问题的解vector<int> dp(n + 1);// 初始状态:预设最小子问题的解dp[1] = 1;dp[2] = 2;// 状态转移:从较小子问题逐步求解较大子问题for (int i = 3; i <= n; i++) {dp[i] = dp[i - 1] + dp[i - 2];}return dp[n]; }

根据以上内容,总结出动态规划的常用术语
- 将数组 d p dp dp 称为 d p dp dp 表, d p [ i ] dp[i] dp[i] 表示状态 i i i 对应子问题的解
- 将最小子问题对应的状态(即第 1 和 2 阶楼梯)称为初始状态
- 将递推公式 d p [ i ] = d p [ i − 1 ] + d p [ i − 2 ] dp[i]=dp[i-1]+dp[i-2] dp[i]=dp[i−1]+dp[i−2] 称为状态转移方程
1.4 空间优化
- 由于 d p [ i ] dp[i] dp[i] 只与 d p [ i − 1 ] dp[i-1] dp[i−1] 和 d p [ i − 2 ] dp[i-2] dp[i−2] 有关,因此无须使用一个数组 dp 来存储所有子问题的解,而只需两个变量滚动前进即可
/* 爬楼梯:空间优化后的动态规划 */ // 空间复杂度从 O(n) 降低至 O(1) int climbingStairsDPComp(int n) {if (n == 1 || n == 2)return n;int a = 1, b = 2;for (int i = 3; i <= n; i++) {int tmp = b;b = a + b;a = tmp;}return b; }
在动态规划问题中,当前状态往往仅与前面有限个状态有关,这时可以只保留必要的状态,通过 “降维” 来节省内存空间,这种空间优化技巧被称为 “滚动变量” 或 “滚动数组”
2. 贪心算法
-
贪心算法是一种常见的解决优化问题的算法,其基本思想是:在问题的每个决策阶段,都选择当前看起来最优的选择,即贪心地做出局部最优的决策,以期望获得全局最优解
-
贪心算法和动态规划都常用于解决优化问题,它们之间的区别如下
- 动态规划会根据之前阶段的所有决策来考虑当前决策,并使用过去子问题的解来构建当前子问题的解
- 贪心算法不会重新考虑过去的决策,而是一路向前地进行贪心选择,不断缩小问题范围,直至问题被解决
问题:给定 n 种硬币,第 i 种硬币的面值为 coins[i-1],目标金额为 amt,每种硬币可以重复选取,问能够凑出目标金额的最少硬币个数,如果无法凑出目标金额则返回 -1

/* 零钱兑换:贪心 */
int coinChangeGreedy(vector<int> &coins, int amt) {// 假设 coins 列表有序int i = coins.size() - 1;int count = 0;// 循环进行贪心选择,直到无剩余金额while (amt > 0) {// 找到小于且最接近剩余金额的硬币while (i > 0 && coins[i] > amt) {i--;}// 选择 coins[i]amt -= coins[i];count++;}// 若未找到可行方案,则返回 -1return amt == 0 ? count : -1;
}
2.1 贪心算法优缺点
-
贪心算法不仅操作直接、实现简单,而且通常效率也很高。在以上代码中,记硬币最小面值为 m i n ( c o i n s ) min(coins) min(coins),则贪心选择最多循环 a m t / m i n ( c o i n s ) amt/min(coins) amt/min(coins) 次,时间复杂度为 O ( a m t / m i n ( c o i n s ) ) O(amt/min(coins)) O(amt/min(coins))。这比动态规划解法的时间复杂度 O ( n ∗ a m t ) O(n*amt) O(n∗amt) 提升了一个数量级
-
然而,对于某些硬币面值组合,贪心算法并不能找到最优解
- 正例 c o i n s = [ 1 , 5 , 10 , 20 , 50 , 100 ] coins = [1, 5, 10, 20, 50, 100] coins=[1,5,10,20,50,100]:在该硬币组合下,给定任意 a m t amt amt,贪心算法都可以找出最优解
- 反例 1 c o i n s = [ 1 , 20 , 50 ] coins = [1, 20, 50] coins=[1,20,50]:假设 a m t = 60 amt = 60 amt=60,贪心算法只能找到 50 + 1 × 10 50 + 1×10 50+1×10 的兑换组合,共计 11 枚硬币,但动态规划可以找到最优解 20 + 20 + 20 20 + 20 + 20 20+20+20,仅需 3 枚硬币
- 反例 2 c o i n s = [ 1 , 49 , 50 ] coins = [1, 49, 50] coins=[1,49,50]:假设 a m t = 98 amt = 98 amt=98,贪心算法只能找到 50 + 1 × 48 50 + 1×48 50+1×48 的兑换组合,共计 49 枚硬币,但动态规划可以找到最优解 49 + 49 49 + 49 49+49,仅需 2 枚硬币

- 一般情况下,贪心算法适用于以下两类问题
- 可以保证找到最优解:贪心算法在这种情况下往往是最优选择,因为它往往比回溯、动态规划更高效
- 可以找到近似最优解:对于很多复杂问题来说,寻找全局最优解是非常困难的,能以较高效率找到次优解也是非常不错的
2.2 贪心典型例题
- 硬币找零问题
- 在某些硬币组合下,贪心算法总是可以得到最优解
- 区间调度问题
- 假设你有一些任务,每个任务在一段时间内进行,你的目标是完成尽可能多的任务。如果每次都选择结束时间最早的任务,那么贪心算法就可以得到最优解
- 分数背包问题
- 给定一组物品和一个载重量,你的目标是选择一组物品,使得总重量不超过载重量,且总价值最大。如果每次都选择性价比最高(价值 / 重量)的物品,那么贪心算法在一些情况下可以得到最优解
- 股票买卖问题
- 给定一组股票的历史价格,你可以进行多次买卖,但如果你已经持有股票,那么在卖出之前不能再买,目标是获取最大利润
- 霍夫曼编码
- 霍夫曼编码是一种用于无损数据压缩的贪心算法。通过构建霍夫曼树,每次选择出现频率最小的两个节点合并,最后得到的霍夫曼树的带权路径长度(即编码长度)最小
- Dijkstra 算法
- 它是一种解决给定源顶点到其余各顶点的最短路径问题的贪心算法
相关文章:

数据结构与算法(十):动态规划与贪心算法
参考引用 Hello 算法 Github:hello-algo 1. 动态规划算法 动态规划将一个问题分解为一系列更小的子问题,并通过存储子问题的解来避免重复计算,从而大幅提升时间效率 问题:给定一个共有 n 阶的楼梯,你每步可以上 1 阶或…...

【C++代码】安排行程,N皇后,解数独--代码随想录
题目:重新安排行程 给你一份航线列表 tickets ,其中 tickets[i] [fromi, toi] 表示飞机出发和降落的机场地点。请你对该行程进行重新规划排序。所有这些机票都属于一个从 JFK(肯尼迪国际机场)出发的先生,所以该行程必…...

SpringCloud Alibaba【二】nacos
nacos配置与使用 nacos初步使用nacos安装与配置创建命名空间 nacos使用与配置创建新项目作为父项目 创建nacos服务端项目pom.xmlapplication.yml启动类 创建nacos客户端项目pom.xml application.yml启动类 启动测试 nacos配置负载均衡改造生产者nacos-provider-projectcontroll…...

C++中的fsanitize指令
一个集成在 gcc、clang 编译器中的编译指令,可以有效测试程序中的一些诸如数组越界、未定义行为等情况。 举个例子: #include <bits/stdc.h> using namespace std;const int maxn2e55,mxr1e5,maxm1e75; int head[maxn],nxt[maxn],to[maxn],f[max…...
【AI视野·今日Robot 机器人论文速览 第五十八期】Thu, 19 Oct 2023
AI视野今日CS.Robotics 机器人学论文速览 Thu, 19 Oct 2023 Totally 25 papers 👉上期速览✈更多精彩请移步主页 Daily Robotics Papers InViG: Benchmarking Interactive Visual Grounding with 500K Human-Robot Interactions Authors Hanbo Zhang, Jie Xu, Yuch…...

Java截取(提取)子字符串(substring()),Java分割字符串(split())
在 String 中提供了两个截取字符串的方法,一个是从指定位置截取到字符串结尾,另一个是截取指定范围的内容。下面对这两种方法分别进行介绍。 1. substring(int beginIndex) 形式 此方式用于提取从索引位置开始至结尾处的字符串部分。调用时,…...
从厨房间到股市:家庭主妇的华美转身
我一直是一个安于现状的家庭主妇。生活中,我热爱烹饪、园艺和照顾家人,但我也渴望能有更多的自我实现和价值感。在机缘巧合下,我接触到了卓扬网,一个专业的股票投资平台。从那刻起,我的人生发生了翻天覆地的变化。 初…...

Oracle 数据库的锁排查方法
关键字 oracle lock 问题描述 Oracle 数据库上锁问题如何排查 解决问题思路 准备数据 create table lock_test(name varchar(10),age varchar(10));insert into lock_test values(ff,10); insert into lock_test values(yy,20); insert into lock_test values(ll,30);Orac…...
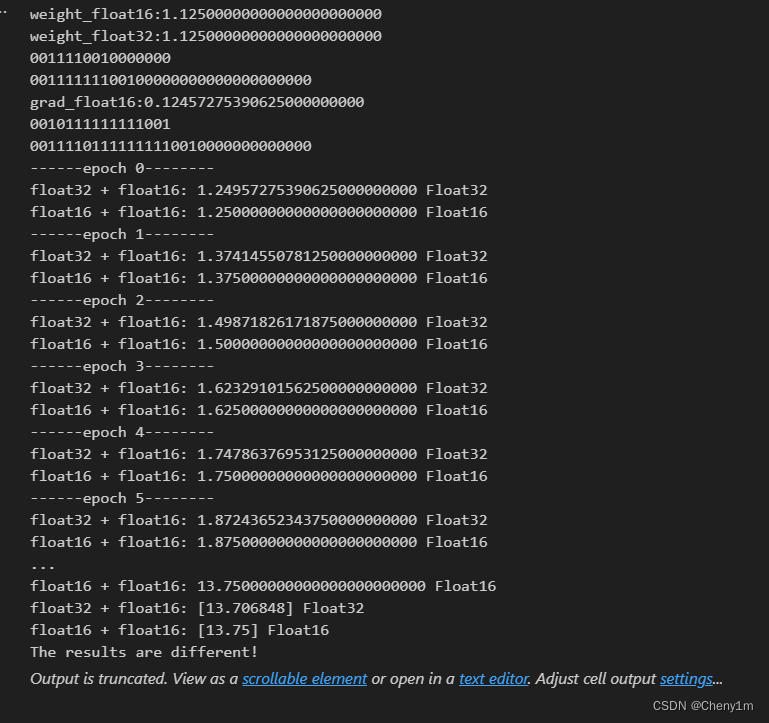
混合精度训练原理之float16和float32数据之间的互相转换
混合精度训练原理之float16和float32数据之间的互相转换 本篇文章参考:全网最全-混合精度训练原理 上述文章已经讲解的比较详细,本文只是从数值角度分析: 1. float32转入float16的精度误差 2. 在深度学习的混精度训练当中,当参数…...
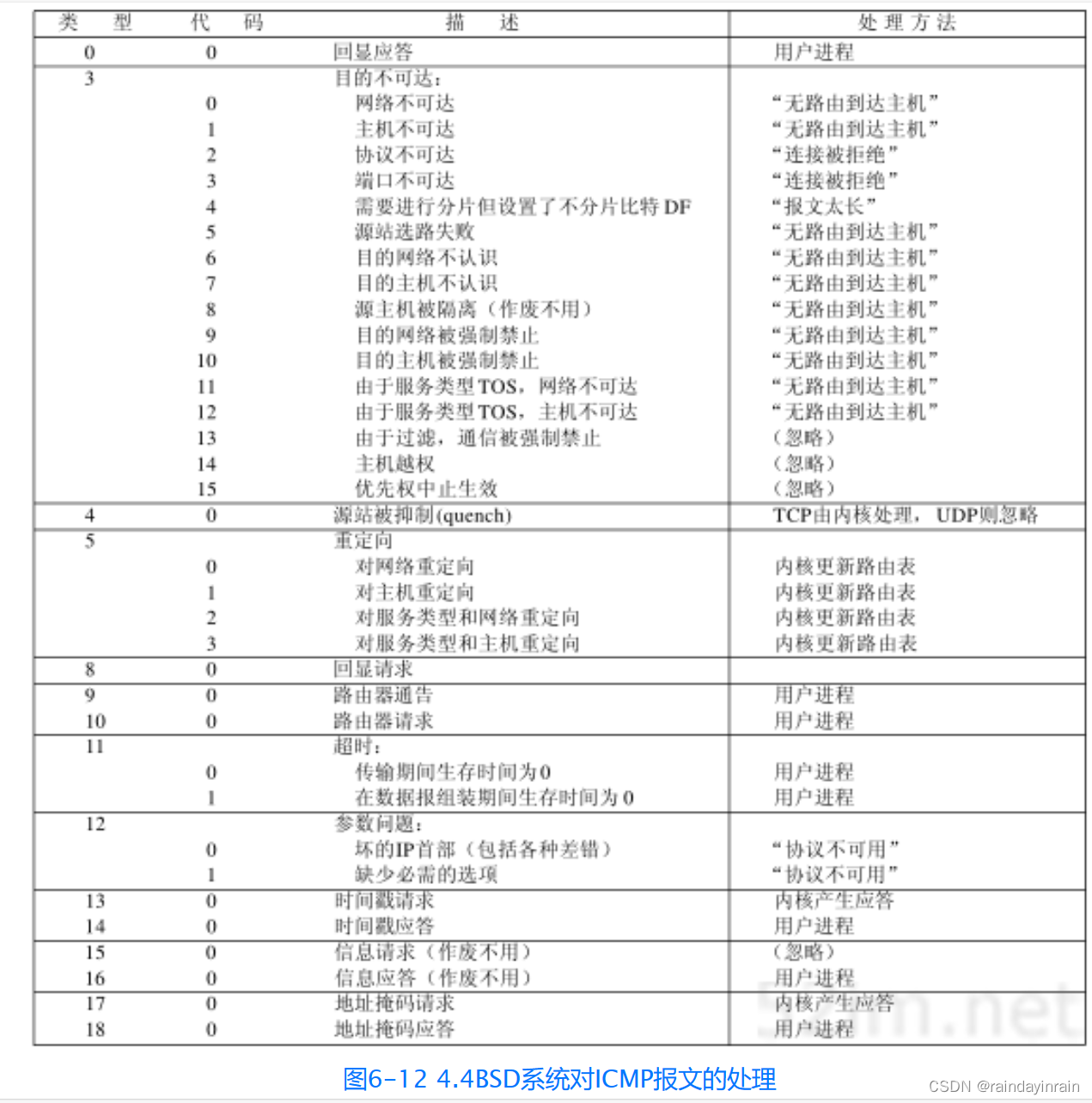
网络协议--ICMP:Internet控制报文协议
6.1 引言 ICMP经常被认为是IP层的一个组成部分。它传递差错报文以及其他需要注意的信息。ICMP报文通常被IP层或更高层协议(TCP或UDP)使用。一些ICMP报文把差错报文返回给用户进程。 ICMP报文是在IP数据报内部被传输的,如图6-1所示。 ICMP…...
《红蓝攻防对抗实战》三.内网探测协议出网之HTTP/HTTPS协议探测出网
目录 一. 在 Windows 操作系统中探测 HTTP/HTTPS 出网 1. Bitsadmin 命令 2.Certuil 命令 2.Linux系统探测HTTP/HTTPS出网 1.Curl命令 2.Wget命令 对目标服务器探测 HTTP/HTTPS 是否出网时,要根据目标系统类型执行命令,不同类型的操作系统使用的探…...
【Win11】系统重装教程(最新最详细)
目录 一.简介 二.用U盘制作PE系统 三、安装系统 软件:Windows 11版本:21H2语言:简体中文大小:5.14G安装环境:PE系统,至少7代处理器硬件要求:CPU2.0GHz 内存4G(或更高)下载通道①丨…...
如何构建一个外卖微信小程序
随着外卖行业的不断发展,越来越多的商家开始关注外卖微信小程序的开发。微信小程序具有使用方便、快速上线、用户覆盖广等优势,成为了商家们的首选。 那么,如何快速开发一个外卖微信小程序呢?下面就让我们来看看吧! 首…...
小知识(5) el-table行样式失效问题
一、实现效果 子级呈现不同颜色去区分 二、最初代码 tips: 我这里使用的vue3 elementplus <el-table :row-class-name"tableRowClassName" >... </el-table>function tableRowClassName({ row, rowIndex }) {if (row.children.length 0) {return …...
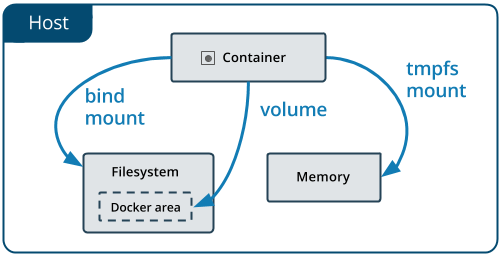
【Docker】Docker数据的存储
默认情况下,在运行中的容器里创建的文件,被保存在一个可写的容器层里,如果容器被删除了,则对应的数据也随之删除了。 这个可写的容器层是和特定的容器绑定的,也就是这些数据无法方便的和其它容器共享。 Docker主要提…...

hive字段关键字问题处理
最近在xxl_job部署shell调度任务时,发现在编写Hql时,对一些使用关键字命名的字段无法解析,按开发规范,字段命名不应该有关键字,但是数据来源是第三方,无法修改,需要通过flume对从kafka的数据到hdfs上,数据是json格式,所以需要对关…...

指定顺序输出
系列文章目录 进阶的卡莎C++_睡觉觉觉得的博客-CSDN博客数1的个数_睡觉觉觉得的博客-CSDN博客双精度浮点数的输入输出_睡觉觉觉得的博客-CSDN博客足球联赛积分_睡觉觉觉得的博客-CSDN博客大减价(一级)_睡觉觉觉得的博客-CSDN博客小写字母的判断_睡觉觉觉得的博客-CSDN博客纸币(…...
(Java)中的数据类型和变量
文章目录 一、字面常量二、数据类型三、变量1.变量的概念2.语法的格式3.整型变量4.长整型变量5.短整型变量6.字节型变量 四、浮点型变量1.双精度浮点数2.单精度浮点数 五、字符型常量六、布尔型变量七、类型转换1.自动类型转换(隐式)2.强制类型转换(显式…...
SHELL脚本编程基础,bilibili王晓春老师课程个人笔记(写比较简单,仅供参考)
文章目录 一、第一天(Shell脚本编程基础)作者视频ppt部分作者视频操作编写一个hello.sh可执行文件使hello.sh可以到处运行没有执行权限的执行方式下载httpd(web服务器)curl字符界面浏览器 命令列表凌乱笔记 作业重点: …...

VS code运行vue项目
要在VS Code中启动Vue项目,您可以按照以下步骤进行操作: 1.打开VS Code,并确保已安装Vue.js插件(如Vetur)。 2.在VS Code的侧边栏中,选择您的Vue项目文件夹,或者使用菜单中的“文件”->“打…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

Monorepo架构: Nx Cloud 扩展能力与缓存加速
借助 Nx Cloud 实现项目协同与加速构建 1 ) 缓存工作原理分析 在了解了本地缓存和远程缓存之后,我们来探究缓存是如何工作的。以计算文件的哈希串为例,若后续运行任务时文件哈希串未变,系统会直接使用对应的输出和制品文件。 2 …...

JDK 17 序列化是怎么回事
如何序列化?其实很简单,就是根据每个类型,用工厂类调用。逐个完成。 没什么漂亮的代码,只有有效、稳定的代码。 代码中调用toJson toJson 代码 mapper.writeValueAsString ObjectMapper DefaultSerializerProvider 一堆实…...
