【ARM 嵌入式 C 入门及渐进 10 -- 冒泡排序 选择排序 插入排序 快速排序 归并排序 堆排序 比较介绍】
文章目录
- 排序算法小结
- 排序算法C实现
排序算法小结
C语言中常用的排序算法包括冒泡排序、选择排序、插入排序、快速排序、归并排序、堆排序。下面我们来一一介绍:
- 冒泡排序(Bubble Sort):冒泡排序是通过比较相邻元素的大小进行排序。如果当前元素比下一个元素大,就交换它们两个的位置。重复这个过程直到最后,最大的元素就会“冒”到数组的最后。然后再从头开始重复这个过程,但是最后一个元素不再考虑。这个过程会一直进行,直到没有元素需要交换,也就是整个数组已经排序完成。冒泡排序的时间复杂度是
O(n^2)。 - 选择排序(Selection Sort):选择排序是每次从未排序的元素中选择最小(或最大)的元素放到未排序元素的开始位置,直到所有元素都已排序。选择排序的时间复杂度也是
O(n^2)。 - 插入排序(Insertion Sort):插入排序的思路是将未排序的元素依次插入到已排序元素的适当位置。开始时,第一个元素被认为已排序,然后将第二个元素和它比较,决定第二个元素在已排序元素中的位置,然后再将第三个元素和已排序的元素比较,依次进行。插入排序的时间复杂度是
O(n^2)。 - 快速排序(Quick Sort):快速排序是一种使用分治策略的排序算法。它的基本思想是选择一个基准元素,将数组分为两部分,一部分的元素都比基准元素小,另一部分的元素都比基准元素大。然后对这两部分再分别进行快速排序。快速排序最坏的时间复杂度是
O(n^2),但是在平均情况下,快速排序的时间复杂度是O(n log n)。 - 归并排序(Merge Sort):归并排序也是一种使用分治策略的排序算法。它的基本思想是将数组分为两半,分别对它们进行归并排序,然后将两个已排序的子数组合并成一个完整的已排序数组。归并排序的时间复杂度是
O(n log n)。 - 堆排序(Heap Sort):堆排序是基于二叉堆的一种排序方法。首先将数组构建成一个最大堆或最小堆,然后依次移除堆顶的元素,并调整堆以保持堆的性质,直到堆为空,此时数组已排序。堆排序的时间复杂度是
O(n log n)。
总的来说,这些排序算法各有各的优点和适用场景,例如,冒泡排序、选择排序和插入排序适用于小规模数据或者部分有序数据,而快速排序、归并排序和堆排序通常适用于大规模数据排序。
排序算法C实现
#include <stdio.h>//冒泡排序:
void bubbleSort(int arr[], int n)
{int i, j;for (i = 0; i < n-1; i++) {for (j = 0; j < n-i-1; j++) {if (arr[j] > arr[j+1]) {int temp = arr[j];arr[j] = arr[j+1];arr[j+1] = temp;}}}
}
//选择排序:
void selectionSort(int arr[], int n)
{int i, j, minIndex, temp;for (i = 0; i < n-1; i++) {minIndex = i;for (j = i+1; j < n; j++) if (arr[j] < arr[minIndex]) {minIndex = j;}temp = arr[minIndex];arr[minIndex] = arr[i];arr[i] = temp;}
}
//插入排序:
void insertionSort(int arr[], int n)
{int i, key, j;for (i = 1; i < n; i++) {key = arr[i];j = i - 1;while (j >= 0 && arr[j] > key) {arr[j + 1] = arr[j];j = j - 1;}arr[j + 1] = key;}
}
//快速排序:
int partition(int arr[], int low, int high)
{int pivot = arr[high];int i = (low - 1);for (int j = low; j <= high- 1; j++) {if (arr[j] <= pivot) {i++;swap(&arr[i], &arr[j]);}}swap(&arr[i + 1], &arr[high]);return (i + 1);
}
void quickSort(int arr[], int low, int high)
{if (low < high) {int pi = partition(arr, low, high);quickSort(arr, low, pi - 1);quickSort(arr, pi + 1, high);}
}
//归并排序:
void merge(int arr[], int l, int m, int r)
{int i, j, k;int n1 = m - l + 1;int n2 = r - m;int L[n1], R[n2];for (i = 0; i < n1; i++) {L[i] = arr[l + i];}for (j = 0; j < n2; j++) {R[j] = arr[m + 1+ j];}i = 0;j = 0;k = l;while (i < n1 && j < n2) {if (L[i] <= R[j]) {arr[k] = L[i];i++;} else {arr[k] = R[j];j++;}k++;}while (i < n1) {arr[k] = L[i];i++;k++;}while (j < n2) {arr[k] = R[j];j++;k++;}
}
void mergeSort(int arr[], int l, int r)
{if (l < r) {int m = l+(r-l)/2;mergeSort(arr, l, m);mergeSort(arr, m+1, r);merge(arr, l, m, r);}
}
//堆排序:
void heapify(int arr[], int n, int i)
{int largest = i;int l = 2*i + 1;int r = 2*i + 2;if (l < n && arr[l] > arr[largest]) {largest = l;}if (r < n && arr[r] > arr[largest]) {largest = r;}if (largest != i) {swap(&arr[i], &arr[largest]);heapify(arr, n, largest);}
}
void heapSort(int arr[], int n)
{for (int i = n / 2 - 1; i >= 0; i--) {heapify(arr, n, i);}for (int i=n-1; i>=0; i--) {swap(&arr[0], &arr[i]);heapify(arr, i, 0);}
}
相关文章:

【ARM 嵌入式 C 入门及渐进 10 -- 冒泡排序 选择排序 插入排序 快速排序 归并排序 堆排序 比较介绍】
文章目录 排序算法小结排序算法C实现 排序算法小结 C语言中常用的排序算法包括冒泡排序、选择排序、插入排序、快速排序、归并排序、堆排序。下面我们来一一介绍: 冒泡排序(Bubble Sort):冒泡排序是通过比较相邻元素的大小进行排…...

虹科 | 解决方案 | 汽车示波器 学校教学方案
虹科Pico汽车示波器是基于PC的设备,特别适用于大课堂的教学、备课以及与师生的互动交流。老师展现讲解波形数据,让学生直观形象地理解汽车的工作原理 高效备课 课前实测,采集波形数据,轻松截图与标注,制作优美的课件&…...
)
广播和组播(多播)
广播 概述 广播(broadcast)是指封包在计算机网络中传输时,目的地址为网络中所有设备的一种传输方式。实际上,这里所说的“所有设备”也是限定在一个范围之中,称为“广播域”。并非所有的计算机网络都支持广播…...
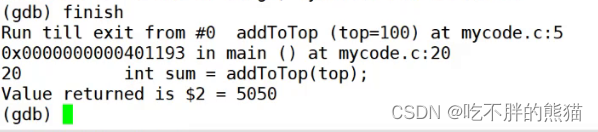
【Linux】gdb调试
目录 进入调试查看代码运行代码断点打断点查断点删断点从一个断点转跳至下一个断点保留断点但不会运行该断点 退出调试逐过程逐语句监视跳转至指定行运行结束当前函数 进入调试 指令:gdb 【可执行文件】: 查看代码 :l 【第几行】如果输入指…...

MySQL创建函数及其使用
MySQL创建函数及其使用 一、MySQL 创建函数二、示例 一、MySQL 创建函数 MySQL 函数是一种可重用的代码块,可以接受输入参数并返回值。你可以在 MySQL 中创建各种类型的函数,包括系统函数、用户定义函数和存储过程。在此处,我们将重点关注用…...
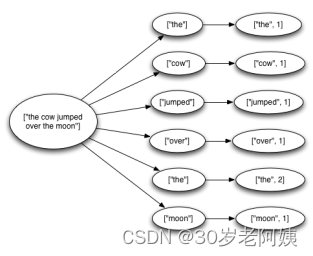
大数据-Storm流式框架(四)---storm容错机制
1、集群节点宕机 Nimbus服务器 硬件 单点故障?可以搭建HA jStorm搭建 nimbus的HA nimbus的信息存储到zookeeper中,只要下游没问题(进程退出)nimbus退出就不会有问题, 如果在nimbus宕机,也不能提交…...
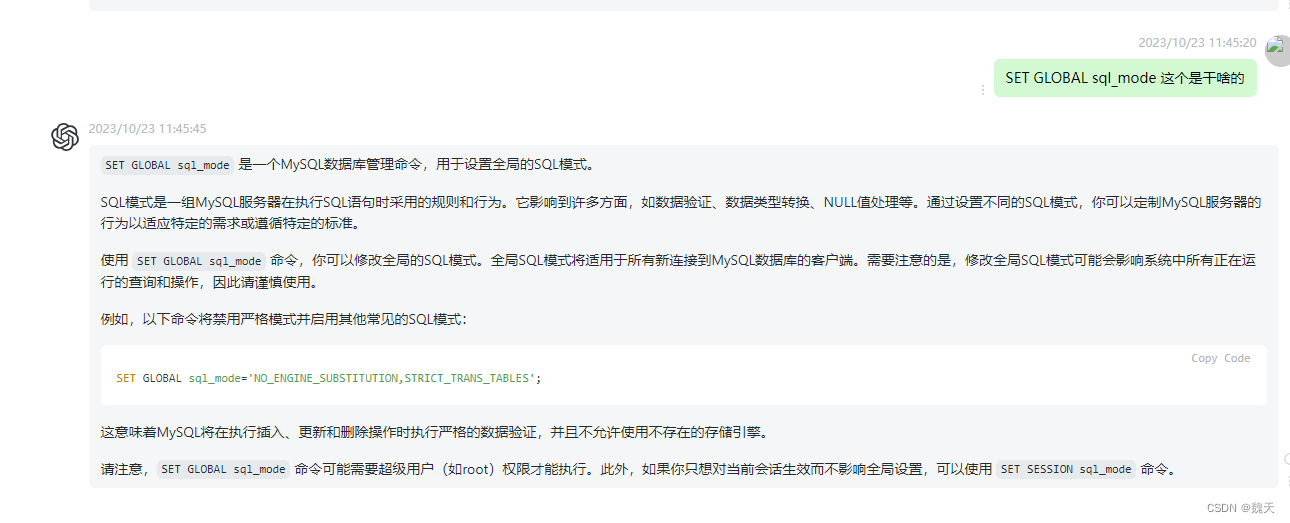
SpringBoot项目把Mysql从5.7升级到8.0
首先你需要把之前的库导入到mysql库导入到8.0的新库中。(导入的时候会报错我是通过navcat备份恢复的) 1、项目中需要修改pom文件的依赖 mysql 和 jdbc <dependency><groupId>mysql</groupId><artifactId>mysql-connector-java&…...

RK3568-适配at24c04模块
将at24c04模块连接到开发板i2c2总线上 i2ctool查看i2c2总线上都有哪些设备 UU表示设备地址的从设备被驱动占用,卸载对应的驱动后,UU就会变成从设备地址。at24c04模块设备地址 0x50和0x51是at24c04模块i2c芯片的设备地址。这个从芯片手册上也可以得知。A0 A1 A2表示的是模块对…...
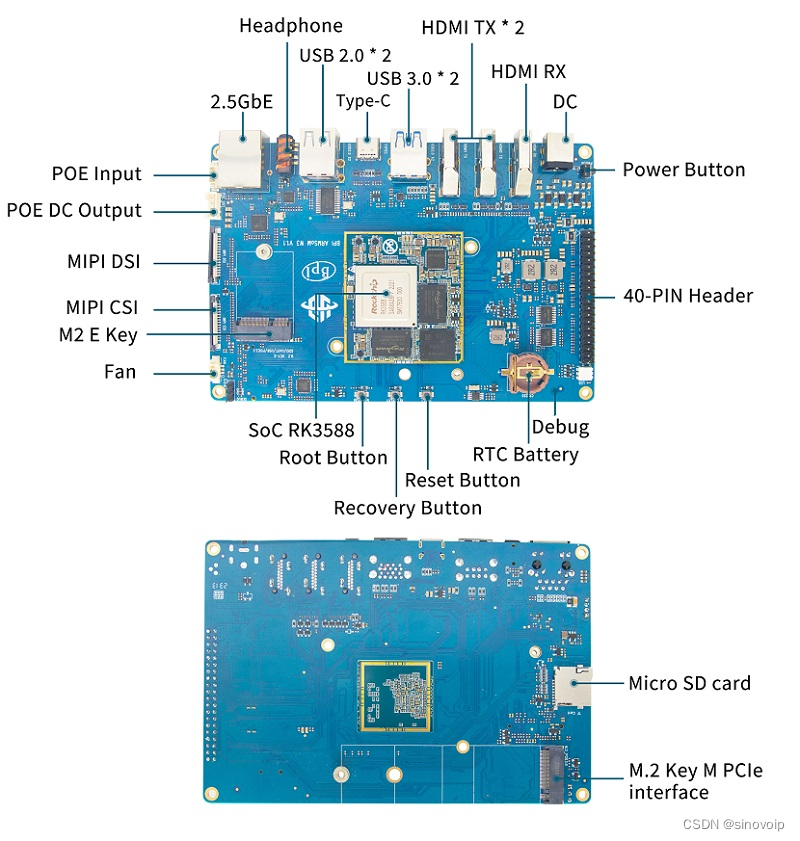
Banana Pi BPI-W3 ArmSoM-W3之RK3588-MIPI-DSI屏幕调试笔记
一. 简介 本文是基于RK3588平台,MIPI屏调试总结。 二. 环境介绍 硬件环境: ArmSoM-W3 RK3588开发板、MIPI-DSI显示屏( ArmSoM官方配件 )软件版本: OS:ArmSoM-W3 Debian11 三. MIPI屏幕调试 3.1 调试总览,调试步骤分…...
Git的远程仓库
Git的远程仓库 添加远程仓库从远程库克隆 添加远程仓库 你在本地创建了一个Git仓库后,又想在GitHub创建一个Git仓库,并且让这两个仓库进行远程同步,这样,GitHub上的仓库既可以作为备份,又可以让其他人通过该仓库来协作…...

Linux虚拟网络设备—Veth Pair
veth是Virtual Ethernet Device的缩写,是一种成对出现的Linux虚拟网络接口设备。它最常用的功能是用于将不同的Linux network namespaces 命名空间网络连接起来,让二个namespaces之间可以进行通信。我们可以简单的把veth pair理解为用一根网线࿰…...

Parcelable protocol requires the CREATOR object to be static on class com.test
对于 Parcelable 协议,确实要求 CREATOR 对象必须是静态的。这是因为在反序列化过程中,需要通过 CREATOR 对象来创建 Parcelable 对象的实例。 根据错误信息,涉及到了com.test类中的问题。通常情况下,如果一个内部类需要实现 Par…...

Python的Matplotlib库:数据可视化的利器
引言: Matplotlib是一款强大的Python库,专为数据可视化而设计。无论是绘制折线图、散点图、柱状图还是饼图,Matplotlib都能提供灵活且易于操作的绘图方法。 1. Matplotlib简介 Matplotlib是Python中最流行的绘图库之一,被广泛应…...

普通人做抖店,需要具备什么条件?一篇详解!
我是电商珠珠 抖音小店的热度一直很高,对于想开店的新手来说,不知道需要什么条件,今天我就来给大家详细的讲一下。 一、营业执照 在入驻抖音小店之前,需要准备一张营业执照。 营业执照一共有两种类型,一种为个体工…...
Django分页功能的使用和自定义分装
1. 在settings中进行注册 # drf配置 REST_FRAMEWORK {DEFAULT_AUTHENTICATION_CLASSES: (# rest_framework_jwt.authentication.JSONWebTokenAuthentication,rest_framework_simplejwt.authentication.JWTAuthentication,rest_framework.authentication.SessionAuthenticatio…...

React-hooks有哪些用法?
React Hooks 是 React 16.8 引入的一种新的特性,用于在函数组件中使用状态和其他 React 特性。下面列举了一些常见的 React Hooks 的用法: 1:useState:用于在函数组件中添加状态。: import React, { useState } from react;function MyComponent() {const [count, setCou…...
)
2024年CFA一级公示表,一级quicksheet(内附分享链接)
随着金融行业的迅速发展,CFA(特许金融分析师)认证成为了许多金融从业者追求的目标。2024年CFA一级公示表资料的自学,为那些渴望在金融领域取得突破的人们提供了宝贵的机会。 通过自学CFA一级公示表资料,我们可以深入了…...

【Kubernetes】 Kubernetes 了解云原生的原理
Kubernetes 了解云原生的原理 云原生是一种软件设计、实施和部署方法,旨在充分利用基于云的服务和交付模型。云原生[1]应用程序通常也使用分布式架构运行。这意味着应用程序功能被分解为多个服务,然后分布在托管环境中,而不是整合到单个服务…...

什么是jquery
jquery是一个javascript库;用来简化javascript编程;基本是前端必备; 看一下示例; <!DOCTYPE html> <html> <head> <meta charset"utf-8"> <script src"https://cdn.staticfile.org/j…...

竞赛选题 深度学习动物识别 - 卷积神经网络 机器视觉 图像识别
文章目录 0 前言1 背景2 算法原理2.1 动物识别方法概况2.2 常用的网络模型2.2.1 B-CNN2.2.2 SSD 3 SSD动物目标检测流程4 实现效果5 部分相关代码5.1 数据预处理5.2 构建卷积神经网络5.3 tensorflow计算图可视化5.4 网络模型训练5.5 对猫狗图像进行2分类 6 最后 0 前言 &#…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...
