浙大陈越何钦铭数据结构06-图1 列出连通集
题目
给定一个有N个顶点和E条边的无向图,请用DFS和BFS分别列出其所有的连通集。假设顶点从0到N−1编号。进行搜索时,假设我们总是从编号最小的顶点出发,按编号递增的顺序访问邻接点。
输入格式:
输入第1行给出2个整数N(0<N≤10)和E,分别是图的顶点数和边数。随后E行,每行给出一条边的两个端点。每行中的数字之间用1空格分隔。
输出格式:
按照"{ v
1
v
2
… v
k
}"的格式,每行输出一个连通集。先输出DFS的结果,再输出BFS的结果。
输入样例:
8 6
0 7
0 1
2 0
4 1
2 4
3 5
输出样例:
{ 0 1 4 2 7 }
{ 3 5 }
{ 6 }
{ 0 1 2 7 4 }
{ 3 5 }
{ 6 }
代码
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>#define MAX_VERTEX_NUM 10
#define ELEMENT_TYPE int
#define ERROR -1
#define QUEUE_SIZE 10typedef int Vertex;struct _Queue
{ELEMENT_TYPE *data;int front, rear;int size;
};
typedef struct _Queue *Queue;struct _Edge
{int v, w;
};
typedef struct _Edge *Edge;struct _MGraph
{int nv, ne;int graph[MAX_VERTEX_NUM][MAX_VERTEX_NUM];
};
typedef struct _MGraph *MGraph;Queue createQueue(ELEMENT_TYPE size);
bool isFull(Queue q);
bool isEmpty(Queue q);
bool addQ(Queue q, ELEMENT_TYPE x);
ELEMENT_TYPE delQ(Queue q);void initVisited(bool visited[]);
bool isEdge(MGraph g, Vertex v, Vertex w);
MGraph createGraph(int numVertices);
void insertEdge(MGraph g, Edge e);
MGraph buildGraph();
void dfs(MGraph g, Vertex v);
void bfs(MGraph g, Vertex s);
void listComponentsViaDFS(MGraph g);
void listComponentsViaBFS(MGraph g);bool visited[MAX_VERTEX_NUM] = {false};/*
06-图1 列出连通集难度:1星
重要度:3星,必须掌握的2种图的遍历方式。无向图,用0,1表示顶点间是否有边8 6
0 7
0 1
2 0
4 1
2 4
3 5{ 0 1 4 2 7 }
{ 3 5 }
{ 6 }
{ 0 1 2 7 4 }
{ 3 5 }
{ 6 }*/
int main()
{MGraph g = buildGraph();listComponentsViaDFS(g);initVisited(visited);listComponentsViaBFS(g);free(g);return 0;
}// 初始化Visited数组,将所有顶点的访问状态初始化为false
void initVisited(bool visited[])
{Vertex v;for (v = 0; v < MAX_VERTEX_NUM; v++)visited[v] = false;
}bool isEdge(MGraph g, Vertex v, Vertex w)
{return g->graph[v][w] == 1;
}MGraph createGraph(int numVertices)
{MGraph g = (MGraph)malloc(sizeof(struct _MGraph));g->nv = numVertices;g->ne = 0;Vertex v, w;for (v = 0; v < g->nv; v++)for (w = 0; w < g->nv; w++)g->graph[v][w] = 0; // 初始化为0,表示无边return g;
}void insertEdge(MGraph g, Edge e)
{ //(V,W)之间双向置为1,表示无向有边g->graph[e->v][e->w] = 1;g->graph[e->w][e->v] = 1;
}MGraph buildGraph()
{MGraph g;Edge e;Vertex v;int nv, ne;scanf("%d %d", &nv, &ne);g = createGraph(nv);if (ne){g->ne = ne;e = (Edge)malloc(sizeof(struct _Edge));for (v = 0; v < g->ne; v++){scanf("%d %d", &e->v, &e->w);insertEdge(g, e);}free(e);}return g;
}void dfs(MGraph g, Vertex v)
{visited[v] = true;printf("%d ", v);Vertex w;for (w = 0; w < g->nv; w++){if (!visited[w] && isEdge(g, v, w)){dfs(g, w);}}
}// 使用深度优先搜索列出连通集
void listComponentsViaDFS(MGraph g)
{Vertex v;for (v = 0; v < g->nv; v++){if (!visited[v]){printf("{ ");dfs(g, v);printf("}\n");}}
}// 广度优先搜索
void bfs(MGraph g, Vertex s)
{Vertex v, w;Queue q = createQueue(g->nv);printf("%d ", s);visited[s] = true;addQ(q, s);while (!isEmpty(q)){v = delQ(q);for (w = 0; w < g->nv; w++){if (!visited[w] && isEdge(g, v, w)){printf("%d ", w);visited[w] = true;addQ(q, w);}}}free(q->data);free(q);
}// 使用广度优先搜索列出连通集
void listComponentsViaBFS(MGraph g)
{Vertex v;for (v = 0; v < g->nv; v++){if (!visited[v]){printf("{ ");bfs(g, v);printf("}\n");}}
}// 创建队列,Size为队列的最大容量
Queue createQueue(ELEMENT_TYPE size)
{Queue q = (Queue)malloc(sizeof(struct _Queue));q->data = (ELEMENT_TYPE *)malloc(size * sizeof(ELEMENT_TYPE));q->front = q->rear = 0;q->size = QUEUE_SIZE;return q;
}// 判断队列是否已满
bool isFull(Queue q)
{return (q->rear + 1) % q->size == q->front;
}// 判断队列是否为空
bool isEmpty(Queue q)
{return q->front == q->rear;
}// 入队操作
bool addQ(Queue q, ELEMENT_TYPE x)
{if (isFull(q)){printf("Full.\n");return false;}else{q->rear = (q->rear + 1) % q->size; // 队尾索引加1,并考虑循环的情况q->data[q->rear] = x; // 将X存入队尾位置return true;}
}// 出队操作
ELEMENT_TYPE delQ(Queue q)
{if (isEmpty(q)){printf("Empty.\n");return ERROR;}else{q->front = (q->front + 1) % q->size; // 队头索引加1,并考虑循环的情况return q->data[q->front]; // 返回队头元素}
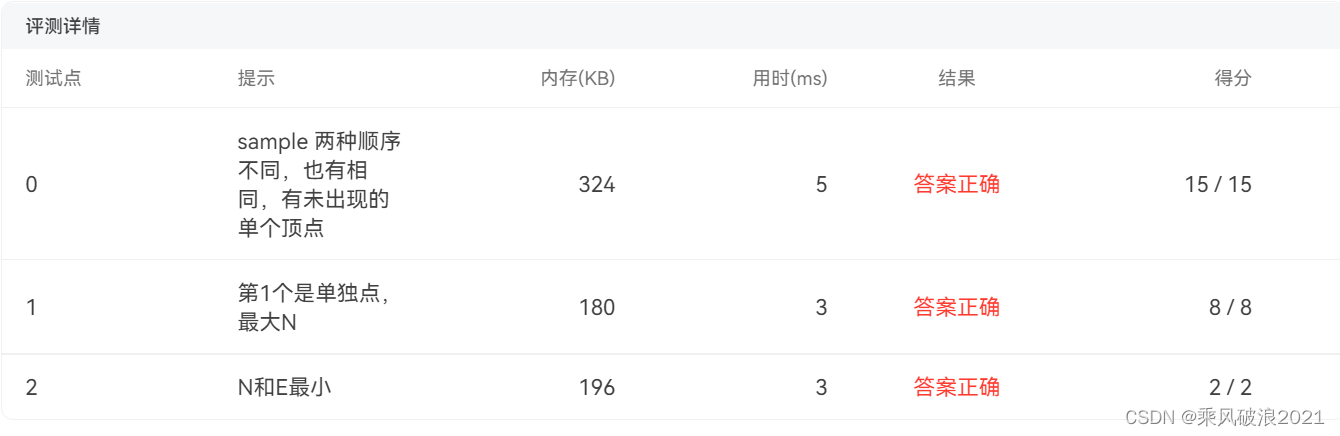
}执行结果
小结
基础的对图的两种方式的遍历,需要熟练掌握。
相关文章:

浙大陈越何钦铭数据结构06-图1 列出连通集
题目 给定一个有N个顶点和E条边的无向图,请用DFS和BFS分别列出其所有的连通集。假设顶点从0到N−1编号。进行搜索时,假设我们总是从编号最小的顶点出发,按编号递增的顺序访问邻接点。 输入格式: 输入第1行给出2个整数N(0<N≤10)和E&…...
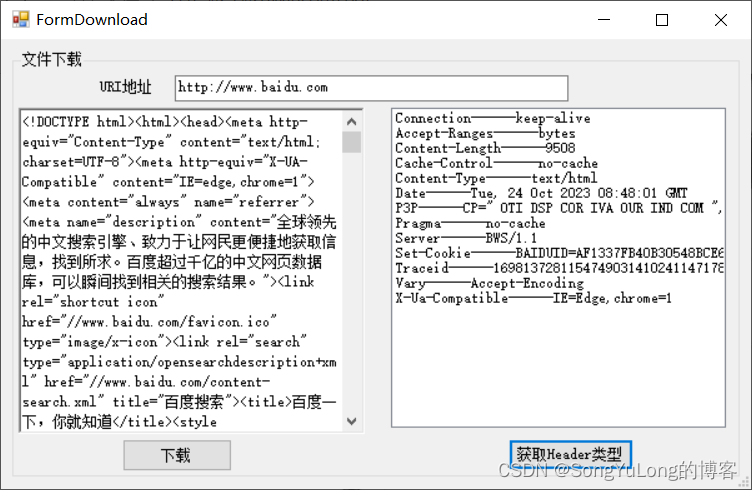
C# Winform编程(9)网络编程
网络编程 HTTP网络编程IPAddress IP地址类WebClient类WebRequest类和WebResponse类 WebBrowser网页浏览器控件TCP网络编程TcpClient类TcpListener类NetworkStream类Socket类 HTTP网络编程 IPAddress IP地址类 IPAddress类代表IP地址,可在十进制表示法和实际的整数…...

RabbitMQ中方法channel.basicAck的使用说明
方法channel.basicAck的作用 在RabbitMQ中,channel.basicAck方法用于确认已经接收并处理了消息。 方法的参数说明 public void basicAck(long deliveryTag,boolean multiple) 参数: long deliveryTag 消息的唯一标识。每条消息都有自己的ID号&#x…...

Jenkins+Python自动化测试持续集成详细教程
Jenkins安装 Jenkins安装 Jenkins是一个开源的软件项目,是基于java开发的一种持续集成工具,用于监控持续重复的工作,旨在提供一个开放易用的软件平台,使软件的持续集成变成可能。由于是基于java开发因此它也依赖java环境&…...
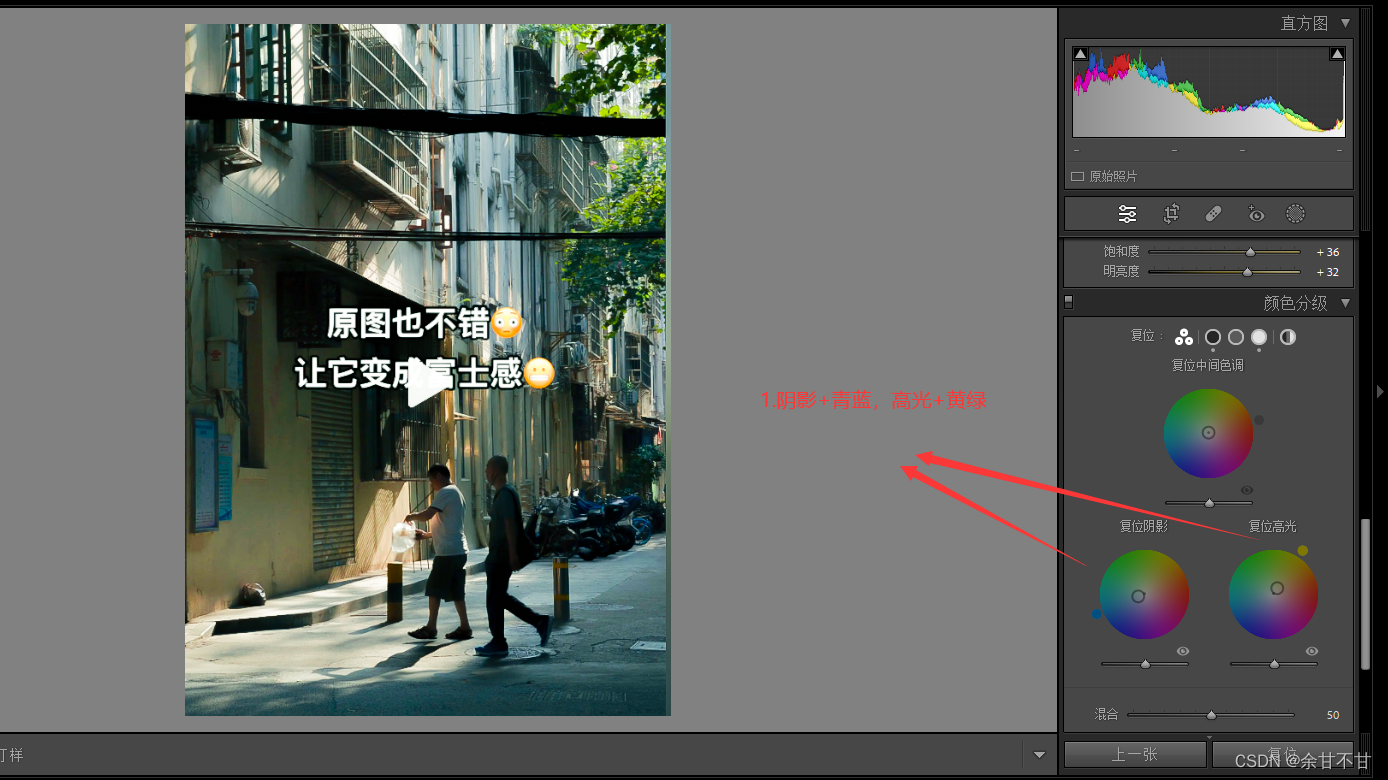
Lightroom学习之路
基础知识 常用快捷键 双击修改图片下右边布局的属性,快速回到初始值 B站学习笔记 1、导入到图库为图片标星级,后期优先处理星级高的图片 2、修改照片-基础-白平衡有吸管吸颜色会自动平衡照片颜色 3、直方图左右上角三角形,选中后照片会显示…...

Day 2 Abp框架下,MySQL数据迁移时,添加表和字段注释
后端采用Abp框架,当前最新版本是7.4.0。 数据库使用MySQL,在执行数据库迁移时,写在Domain层的Entity类上的注释通通都没有,这样查看数据库字段的含义时,就需要对照代码来看,有些不方便。今天专门来解决这个…...
传智教育研究院重磅发布Java学科新研发《智慧养老》项目
在招聘Java开发人才的过程中,企业往往对候选人的项目经验有着严格的要求,项目经验成为顺利就业的重要敲门砖之一。而在数字化技术的学习中,如何让学员通过项目课程有效地积累实战开发经验,就成了数字化技术职业教育的一个重大难点…...
Fiddler抓包VSCode和探索
前言: 最近在使用 VSCode 调试 web 程序时,遇到一些问题,当时不知道如何是好。所以决定抓看来看一看,然后一顿操作猛如虎,成功安装了抓包软件 – Fiddler Classic。我并没有使用 Postman 这种重量级的 HTTP 测试软件&a…...

Pytorch指定数据加载器使用子进程
torch.utils.data.DataLoader(train_dataset, batch_sizebatch_size, shuffleTrue,num_workers4, pin_memoryTrue) num_workers 参数是 DataLoader 类的一个参数,它指定了数据加载器使用的子进程数量。通过增加 num_workers 的数量,可以并行地读取和预处…...

【科普】干货!带你从0了解移动机器人(六) (底盘结构类型)
牵引式移动机器人(AGV/AMR),通常由一个牵引车和一个或多个被牵引的车辆组成。牵引车是机器人的核心部分,它具有自主导航和定位功能,可以根据预先设定的路径或地标进行导航,并通过传感器和视觉系统感知周围环…...
爆肝整理,Pytest+Allure+Jenkins自动化测试集成实战(图文详细步骤)
目录:导读 前言一、Python编程入门到精通二、接口自动化项目实战三、Web自动化项目实战四、App自动化项目实战五、一线大厂简历六、测试开发DevOps体系七、常用自动化测试工具八、JMeter性能测试九、总结(尾部小惊喜) 前言 1、简介 pytesta…...
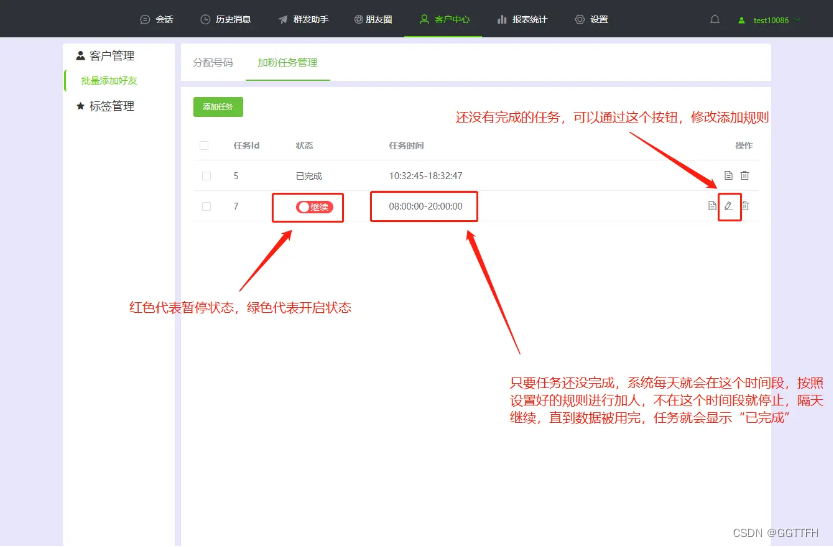
微信批量添加好友,让你的人脉迅速增长
在这个数字化时代,微信作为中国最流行的社交平台之一,已经成为了人们生活中不可或缺的一部分。它的广泛使用为我们提供了无限的社交可能性。你是否曾为了扩大人脉圈子而犯愁?今天,我将向你揭示一个高效添加微信好友的秘密武器&…...
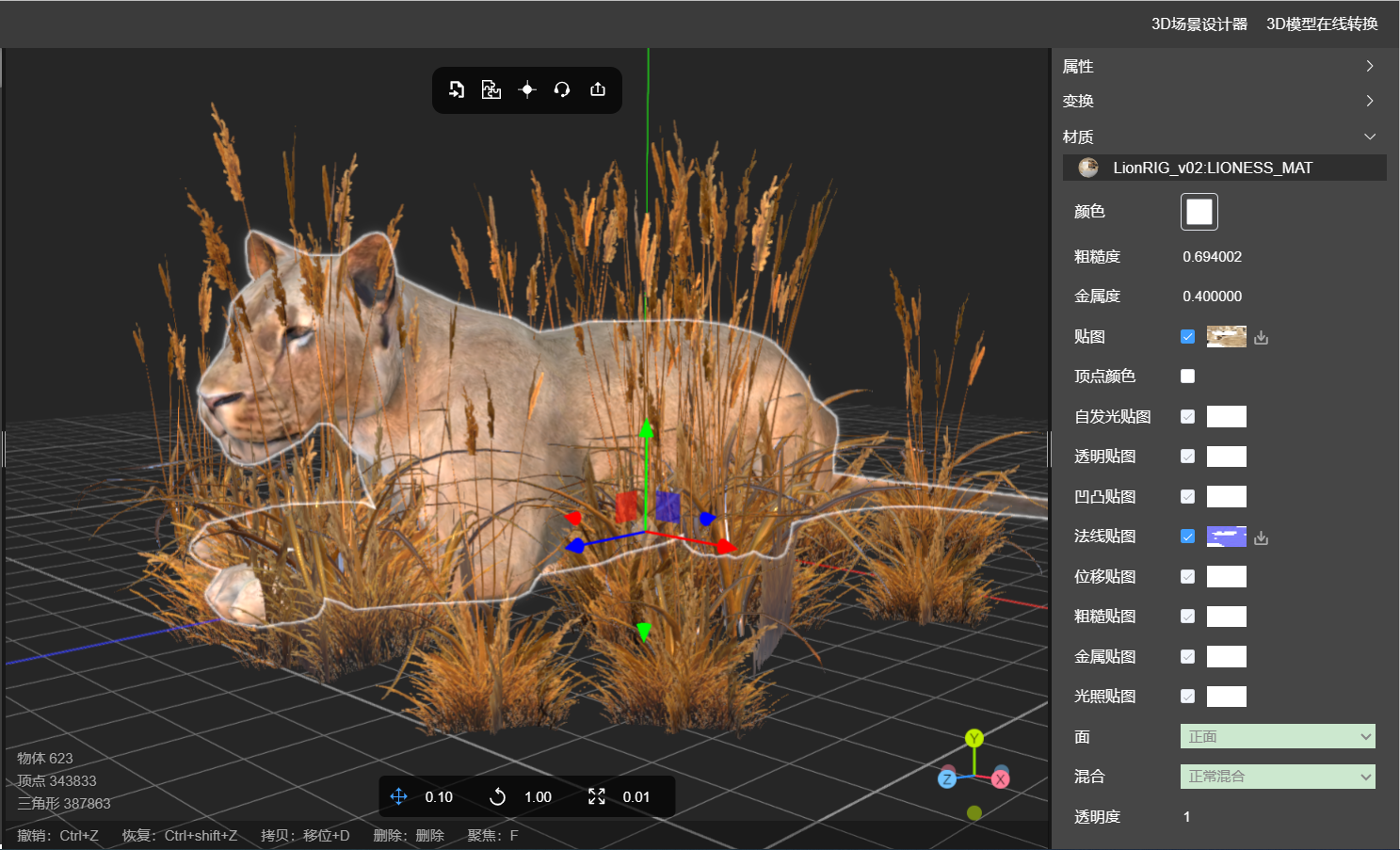
3D模型怎么贴法线贴图?
1、法线贴图的原理? 法线贴图(normal mapping)是一种计算机图形技术,用于在低多边形模型上模拟高多边形模型的细节效果。它通过在纹理坐标上存储和应用法线向量的信息来实现。 法线贴图的原理基于光照模型。在渲染过程中&#x…...

QT中文乱码解决方案与乱码的原因
相信大家应该都遇到过中文乱码的问题,有时候改一改中文就不乱码了,但是有时候用同样的方式还是乱码,那么这个乱码到底是什么原因,又该如何彻底解决呢? 总结 先总结一下: Qt5中,将QString()的构…...
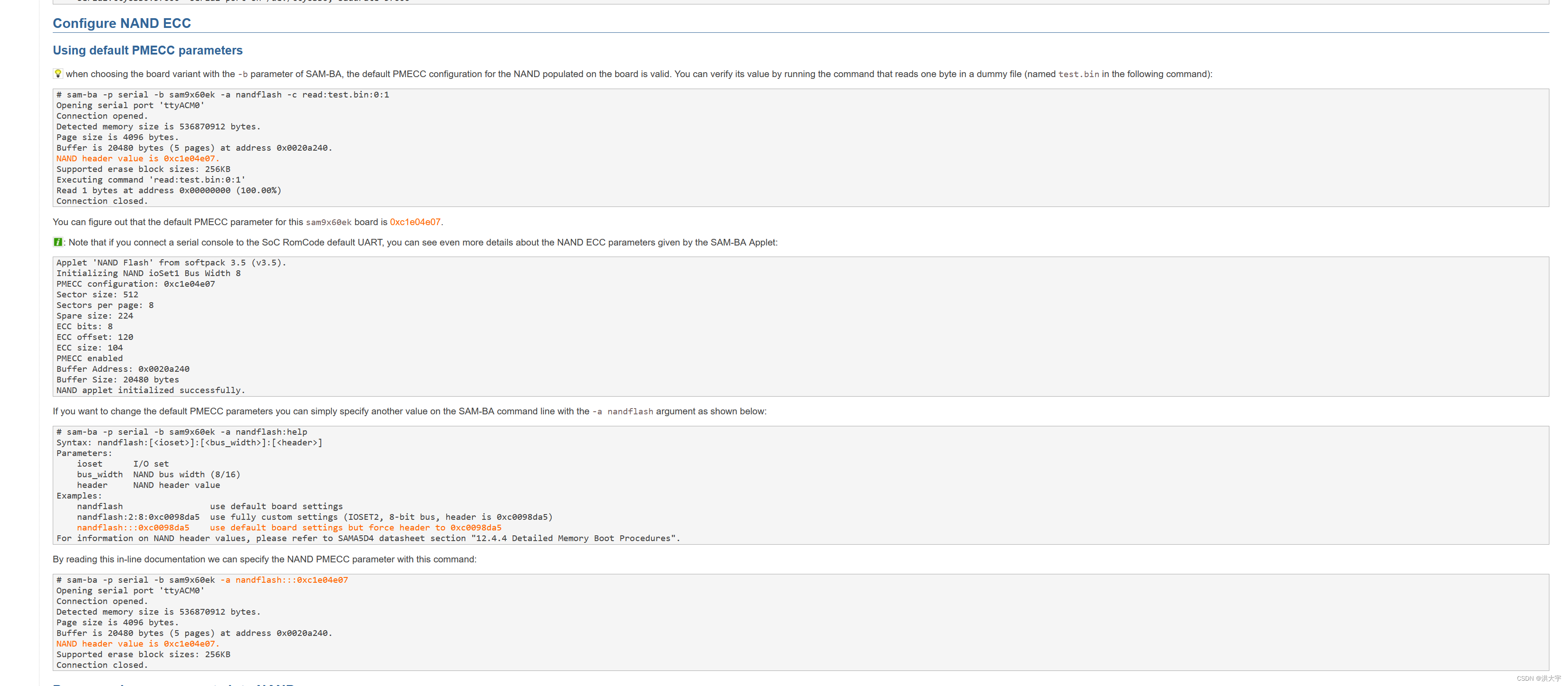
sam9x60 boot
...
3D模型格式转换工具HOOPS Exchange:支持国际标准STEP格式!
HOOPS Exchange SDK是一组C软件库,使开发团队能够快速将可靠的2D和3D CAD导入和导出添加到其应用程序中,访问广泛的数据,包括边界表示 (B-REP)、产品制造信息 (PMI)、模型树、视图、持久 ID、样式、构造几何、可视化等,无需依赖任…...

java--死循环与循环嵌套
1.死循环 可以一直执行下去的一种循环,如果没有干预不会停下来的 2.死循环的写法 3.循环嵌套 循环中又包含循环 4.循环嵌套的特点 外部循环每循环一次,内部循环会全部执行完一轮...

基于机器视觉的图像拼接算法 计算机竞赛
前言 图像拼接在实际的应用场景很广,比如无人机航拍,遥感图像等等,图像拼接是进一步做图像理解基础步骤,拼接效果的好坏直接影响接下来的工作,所以一个好的图像拼接算法非常重要。 再举一个身边的例子吧,…...

基于arduino uno + L298 的直流电机驱动proteus仿真设计
一、L298简介: L298是一个集成的单片电路,采用15个导线多瓦和PowerSO20封装。它是一个高电压、高电流双全桥驱动器,旨在接受标准TTL逻辑电平和驱动感应负载,如继电器、螺线管、直流和加速电机。提供两个使输入来使独立于输入信号的…...
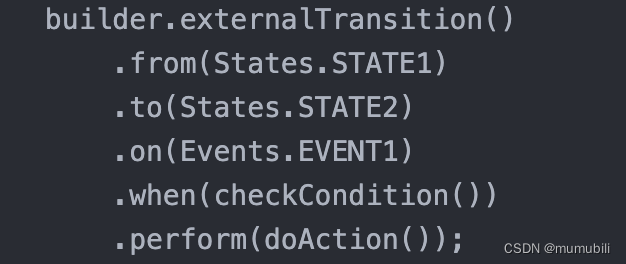
cola架构:有限状态机(FSM)源码分析
目录 0. cola状态机简述 1.cola状态机使用实例 2.cola状态机源码解析 2.1 语义模型源码 2.1.1 Condition和Action接口 2.1.2 State 2.1.3 Transition接口 2.1.4 StateMachine接口 2.2 Builder模式 2.2.1 StateMachine Builder模式 2.2.2 ExternalTransitionBuilder-…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...

C++--string的模拟实现
一,引言 string的模拟实现是只对string对象中给的主要功能经行模拟实现,其目的是加强对string的底层了解,以便于在以后的学习或者工作中更加熟练的使用string。本文中的代码仅供参考并不唯一。 二,默认成员函数 string主要有三个成员变量,…...

跨平台商品数据接口的标准化与规范化发展路径:淘宝京东拼多多的最新实践
在电商行业蓬勃发展的当下,多平台运营已成为众多商家的必然选择。然而,不同电商平台在商品数据接口方面存在差异,导致商家在跨平台运营时面临诸多挑战,如数据对接困难、运营效率低下、用户体验不一致等。跨平台商品数据接口的标准…...

【多线程初阶】单例模式 指令重排序问题
文章目录 1.单例模式1)饿汉模式2)懒汉模式①.单线程版本②.多线程版本 2.分析单例模式里的线程安全问题1)饿汉模式2)懒汉模式懒汉模式是如何出现线程安全问题的 3.解决问题进一步优化加锁导致的执行效率优化预防内存可见性问题 4.解决指令重排序问题 1.单例模式 单例模式确保某…...

【靶场】XXE-Lab xxe漏洞
前言 学习xxe漏洞,搭了个XXE-Lab的靶场 一、搭建靶场 现在需要登录,不知道用户名密码,先随便试试抓包 二、判断是否存在xxe漏洞 1.首先登录抓包 看到xml数据解析,由此判断和xxe漏洞有关,但还不确定xxe漏洞是否存在。 2.尝试xxe 漏洞 判断是否存在xxe漏洞 A.send to …...
