leetcode 困难 —— 数组中的逆序对(分治法)
题目:
在数组中的两个数字,如果前面一个数字大于后面的数字,则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数。
题解:
① 我最开始想的蠢方法(会超时,可跳过)
首先题目求的逆序对,这考虑的关键应该就是 位置 和 大小
那么我们先将大小排个序,然后从小到大考虑
然后我们按数字从小到大放到由位置排序的容器中
每一次放入,二分搜索当前要放入值的位置,其之后的值的数量,就是该值组成的逆序对数量
这样是不是可以只用考虑位置(因为之前放入容器的值的大小都小于当前值)
这样排序 O(nlogn),然后每次放入值前二分搜索 O(nlogn),但是还是超时了
应该是那个 insert 复杂度太高了,没办法,vector 的 insert 复杂度为 O(n)
想过用其他容器,但好像都不能解决,要是大佬有方法,欢迎评论私信,真想不出来 😟
代码如下:
class Solution {
public:vector<pair<int, int> > temp1;vector<pair<int, int> > temp2;int reversePairs(vector<int>& nums) {int res = 0;for(int i = 0; i < nums.size(); i++) {temp1.push_back(make_pair(nums[i], i));}sort(temp1.begin(), temp1.end());for(int i = 0; i < temp1.size(); i++) {pair<int, int> t = make_pair(temp1[i].second, temp1[i].first);int f = lower_bound(temp2.begin(), temp2.end(), t) - temp2.begin();res = res + i - f;temp2.insert(temp2.begin() + f, t);}return res;}
};
② 分治法(害,我这笨脑子,真的想不到啊)
分治排序都知道吧
我们在排序的过程中,考虑逆序对数量
首先两个有序的序列,求逆序对数量
左边的序列中的某个值所组成逆序对等于右边所有小于它的值的数量
可以通过分治法求解的原理,即
局部的排序,不会影响这部分和其他部分组成逆序对
代码如下:
class Solution {
public:vector<int> numbers;int res = 0;void solve(int l, int r) {int mid = (r + l) / 2;if(r - l > 1) {solve(l, mid);solve(mid, r);}else {return;}vector<int> temp;int flag1 = l, flag2 = mid;while(flag1 < mid) {while(flag2 < r && numbers[flag1] > numbers[flag2]) {temp.push_back(numbers[flag2]);flag2++;}temp.push_back(numbers[flag1]);flag1++;res = res + flag2 - mid;}while(flag2 < r) {temp.push_back(numbers[flag2]);flag2++;}for(int i = l; i < r; i++) {numbers[i] = temp[i - l];}}int reversePairs(vector<int>& nums) {numbers = nums;solve(0, nums.size());return res;}
};
相关文章:
)
leetcode 困难 —— 数组中的逆序对(分治法)
题目: 在数组中的两个数字,如果前面一个数字大于后面的数字,则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数。 题解: ① 我最开始想的蠢方法(会超时,可跳过ÿ…...

02.24:图片的风格转换
Github网址:https://github.com/lengstrom/fast-style-transfer 在anaconda prompt中切换环境命令:activate 环境名 列出所有环境名:conda info --envs 安装环境:conda create -n 环境名 pythonx.x.x 删除某环境:co…...
[SSD综述 1.3] SSD及固态存储技术半个世纪发展史
在我们今天看来,SSD已不再是个新鲜事物。这多亏了存储行业的前辈们却摸爬滚打了将近半个世纪,才有了SSD的繁荣, 可惜很多前辈都没有机会看到。所有重大的技术革新都是这样,需要长期的技术积累,一代一代的工程师们默默的…...
题目有bug)
PAT 1023 组个最小数(分数20)题目有bug
目录 题目描述: 题目讲解: 框架构建: 代码部分: 一个bug: 题目描述: 给定数字 0-9 各若干个。你可以以任意顺序排列这些数字,但必须全部使用。目标是使得最后得到的数尽可能小(…...

QML 中的 5 大布局
作者: 一去、二三里 个人微信号: iwaleon 微信公众号: 高效程序员 在 QML 中,可以通过多种方式对元素进行布局 - 手动定位、坐标绑定定位、锚定位(anchors)、定位器和布局管理器。 说到 anchors,可能很多人都不太了解,它是 QML 中一个非常重要的概念,主要提供了一种相…...
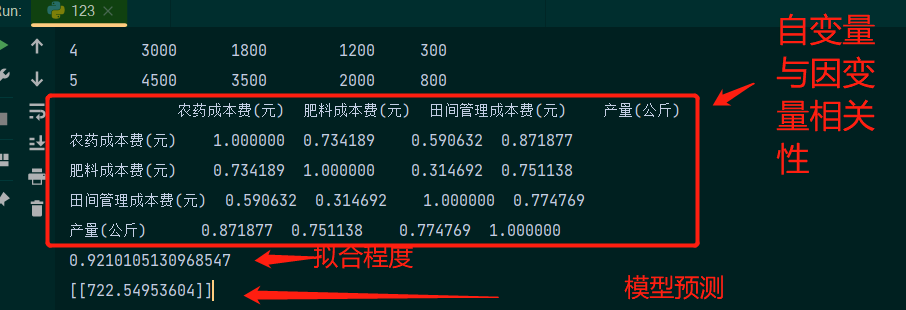
使用Python进行数据分析——线性回归分析
大家好,线性回归是确定两种或两种以上变量之间互相依赖的定量关系的一种统计分析方法。根据自变量的个数,可以将线性回归分为一元线性回归和多元线性回归分析。一元线性回归:就是只包含一个自变量,且该自变量与因变量之间的关系是…...

我眼中的柔宇科技
关注、星标公众号,直达精彩内容来源:技术让梦想更伟大作者:李肖遥很早就知道了柔宇科技,当时是因为知道创始人刘自鸿,23岁清华本硕毕业,26岁获斯坦福大学电子工程博士学位,历时不超过3年&#x…...
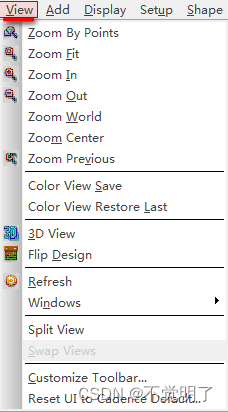
Allegro如何快速把视图居中显示操作指导
Allegro如何快速把视图居中显示操作指导 用Allegro进行PCB设计的时候,为了方便检查和设计,时常需要将视图居中显示。一般地,会使用鼠标的中键进行放大和缩小,或者使用Zoom in和Zoom out来调整视图 Allegro还支持快速将视图居中 具体操作如下 点击View...

搜索相关功能
一、进入搜索页面 1.1 在pages下创建搜索页面为:search 1.2 在index.vue中点击进入搜素页面 onNavigationBarButtonTap(e){if(e.floatleft){uni.navigateTo({url:/pages/search/search})}},1.3 在pages.json中配置搜索页面头部 {"path" : "pages/…...

【从零开始制作 bt 下载器】一、了解 torrent 文件
【从零开始制作 bt 下载器】一、了解 torrent 文件写作背景了解 torrent 文件认识 bencodepython 解析 torrent 文件解密 torrent 文件结尾写作背景 最先开始是朋友向我诉说使用某雷下载结果显示因为版权无法下载,找其他的下载器有次数限制,于是来询问我…...

SystemVerilog-时序逻辑建模(5)多个时钟和时钟域交叉
数字硬件建模SystemVerilog-时序逻辑建模(5)多个时钟和时钟域交叉数字门级电路可分为两大类:组合逻辑和时序逻辑。锁存器是组合逻辑和时序逻辑的一个交叉点,在后面会作为单独的主题处理。组合逻辑描述了门级电路,其中逻…...
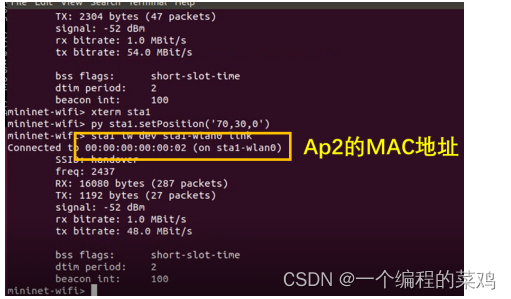
基本中型网络的仿真(RYU+Mininet的SDN架构)-以校园为例
目录 具体问题可以私聊博主 一、设计目标 1.1应用场景介绍 1.2应用场景设计要求 网络配置方式 网络技术要求 网络拓扑要求 互联互通 二、课程设计内容与原理 (1)预期网络拓扑结构和功能 (1)网络设备信息 …...

西北工业大学大学物理(II)期末试题选填解析2021-2022
2 金属薄片,就暗示了载流子是电子了。3 熟练掌握左右手即可。4 又是位移电流。6 感应电场。随时间变化着的磁场能在其周围空间激发一种电场,它能对处于其中的带电粒子施以力的作用,这就是涡旋电场,又叫感生电场。涡旋电场是非保守…...
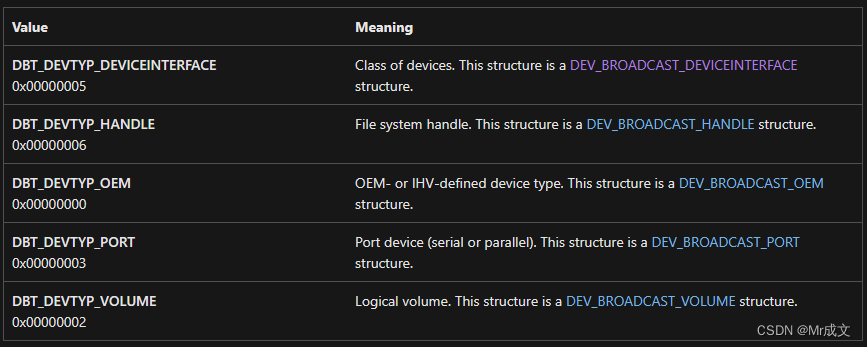
【USB】windows热插拔通知接口分析
文章目录接口介绍概述过滤器介绍举例接收通知创建窗口参考文档接口介绍 概述 window提供了RegisterDeviceNotificationW方法,可以用来监听设备的热插拔事件。 HDEVNOTIFY RegisterDeviceNotificationW([in] HANDLE hRecipient,[in] LPVOID NotificationFilter,[in]…...

CMake入门
课程地址 文档地址 CMake可以用于所有的编程语言 HelloWorld 编写一个C文件: //hello.cpp #include <iostream>int main() {std::cout << "hello, world" <<std::endl;return 0; }手动编译: c hello.cpp书写CMakeList…...

python中一种编写config文件并及时更新的方法
contents0. Intro1. config.py2. 调用以及更新0. Intro 在pytorch或者其他深度学习框架中,有许多超参数需要调整,包括learning_rate,training_data_path等,因此编写一个config文件统一存放这些参数,方便调用/查看/修改…...
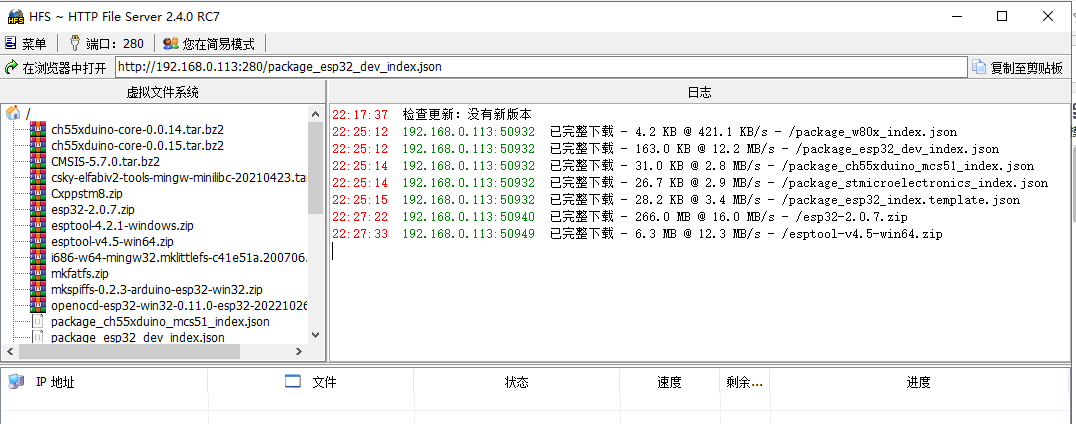
基于Windows下离线安装当前最新Arduino ESP32 SDK(2.0.7)固件开发包
基于Windows下离线安装当前最新Arduino ESP32 SDK(2.0.7)固件开发包✨写这篇的文章的初衷,是由于在前几天想通过离线一键安装包方式实现升级安装,结果发现解压后,可以找到开发板,但是无法上传代码ÿ…...
)
Android 9.0 app添加校验锁(输入密码才能进入app)
1.概述 在9.0的系统rom定制化开发中,在一些产品开发中,需要对app启动校验密码,输入密码后,才可以进app,所以说对这种 开发需求,首先找到启动app的关键点以后,在加入限制app启动的弹窗,输入密码,密码正确后在进入app,实现流程 就是这样,接下来看如何实现的 2.app添加校…...

注意力机制详解系列(二):通道注意力机制
👨💻作者简介: 大数据专业硕士在读,CSDN人工智能领域博客专家,阿里云专家博主,专注大数据与人工智能知识分享。 🎉专栏推荐: 目前在写CV方向专栏,更新不限于目标检测、…...

动态规划-规划兼职工作
动态规划-规划兼职工作 一、问题描述 你打算利用空闲时间来做兼职工作赚些零花钱。这里有 n 份兼职工作,每份工作预计从 startTime 开始到 endTime 结束,报酬为 profit。给你一份兼职工作表,包含开始时间 startTime,结束时间 en…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...

NPOI操作EXCEL文件 ——CAD C# 二次开发
缺点:dll.版本容易加载错误。CAD加载插件时,没有加载所有类库。插件运行过程中用到某个类库,会从CAD的安装目录找,找不到就报错了。 【方案2】让CAD在加载过程中把类库加载到内存 【方案3】是发现缺少了哪个库,就用插件程序加载进…...

android13 app的触摸问题定位分析流程
一、知识点 一般来说,触摸问题都是app层面出问题,我们可以在ViewRootImpl.java添加log的方式定位;如果是touchableRegion的计算问题,就会相对比较麻烦了,需要通过adb shell dumpsys input > input.log指令,且通过打印堆栈的方式,逐步定位问题,并找到修改方案。 问题…...

Vite中定义@软链接
在webpack中可以直接通过符号表示src路径,但是vite中默认不可以。 如何实现: vite中提供了resolve.alias:通过别名在指向一个具体的路径 在vite.config.js中 import { join } from pathexport default defineConfig({plugins: [vue()],//…...
