当前位置： 首页 > news >正文

【强化学习】08——规划与学习（采样方法|决策时规划）

news 2025/9/20 23:32:51

文章目录

  • 优先级采样
    • Example1 Prioritized Sweepingon Mazes
    • 局限性及改进
  • 期望更新和采样更新
    • 不同分支因子下的表现
  • 轨迹采样
  • 总结
  • 实时动态规划
    • Example2 racetrack
  • 决策时规划
    • 启发式搜索
    • Rollout算法
    • 蒙特卡洛树搜索
  • 参考

先做个简单的笔记整理，以后有时间再补上细节

优先级采样

均匀随机采样（uniformly sampling）会使得部分采样的结果对实际的更新毫无作用。如下图所示，在开始时，只有靠近终点部分的更新会产生作用，而其他情况则不会。因此，模拟的经验和更新应集中在一些特殊的状态动作。

在这里插入图片描述
可以使用后向聚焦（backward focusing）进行更好地更新。 后向聚焦是指很多状态的值发生变化带动前继状态的值发生变化。但有的值改变很多，有的改变很少，因此需要根据紧急程度，给这些更新设置优先度进行更新。

优先级采样（Prioritized Sweeping）可以解决上述问题。优先级采样通过设置优先级更新队列，根据值改变的幅度定义优先级： P ← ∣ R + γ max ⁡ a Q ( S ′ , a ) − Q ( S , A ) ∣ P\leftarrow\left|R+\gamma\max_aQ\left(S^{\prime},a\right)-Q(S,A)\right| P← ​R+γamax​Q(S′,a)−Q(S,A) ​

算法伪代码：
在这里插入图片描述

Example1 Prioritized Sweepingon Mazes

在这里插入图片描述

  • 横轴代表格子世界的大小
  • 纵轴代表收敛到最优策略的更新次数
  • 优先级采样收敛更快

局限性及改进

优先级采样在随机环境中利用期望更新（expected updates）的方法。但这样会浪费很多计算资源在一些低概率的状态转移（transitions）上，因此引入采样更新（sample updates）。

期望更新和采样更新

在这里插入图片描述
期望更新

  • Q ( s , a ) ← ∑ s ′ , r p ^ ( s ′ , r ∣ s , a ) [ r + γ max ⁡ a ′ Q ( s ′ , a ′ ) ] . Q(s,a)\leftarrow\sum_{s',r}\hat{p}(s',r|s,a)\Big[r+\gamma\max_{a'}Q(s',a')\Big]. Q(s,a)←s′,r∑​p^​(s′,r∣s,a)[r+γa′max​Q(s′,a′)].
  • 需要知道准确的分布模型
  • 需要更大的计算量
  • 没有偏差更准确

采样更新

  • Q ( s , a ) ← Q ( s , a ) + α [ R + γ max ⁡ a ′ Q ( S ′ , a ′ ) − Q ( s , a ) ] , Q(s,a)\leftarrow Q(s,a)+\alpha\Big[R+\gamma\max_{a'}Q(S',a')-Q(s,a)\Big], Q(s,a)←Q(s,a)+α[R+γa′max​Q(S′,a′)−Q(s,a)], • 只需要采样模型
    • 计算量需求更低
    • 受到采样误差(sampling error)的影响

不同分支因子下的表现

设定
• 𝑏 个后续状态等可能
• 初始估计误差为1
• 下一个状态值假设估计正确
在这里插入图片描述
结果
• 分支因子越多，采样更新越接近期望更新
• 大的随机分支因子和状态数量较多的情况下, 采样更新更好

越复杂的环境越适合进行采样更新。

轨迹采样

在这里插入图片描述

  • 动态规划
    • 对整个状态空间进行遍历
    • 没有侧重实际需要关注的状态上
  • 在状态空间中按照特定分布采样
    • 根据当前策略下所观测的分布进行采样

在这里插入图片描述

轨迹采样

  • 状态转移和奖励由模型决定
  • 动作由当前的策略决定

优点
• 不需要知道当前策略下状态的分布
• 计算量少，简单有效
缺点
• 不断重复更新已经被访问的状态

在这里插入图片描述

  • 不同的分支因子下的表现
  • 确定性环境中表现比较好

总结

  • 优先级采样
    • 收敛更快
    • 随机环境使用期望更新，计算量大
  • 期望更新和采样更新
    • 期望更新计算量大但是没有偏差
    • 采样更新计算量小但是存在采样偏差
  • 轨迹采样
    • 采样更新，计算量小
    • 不断重复某些访问过的状态

实时动态规划

和传统动态规划的区别
• 实时的轨迹采样
• 只更新轨迹访问的状态值

优势
• 能够跳过策略无关的状态
• 在解决状态集合规模大的问题上具有优势
• 满足一定条件下可以以概率1收敛到最优策略

Example2 racetrack

在这里插入图片描述

决策时规划

背景规划（Background Planning）
• 规划是为了更新很多状态值供后续动作的选择
• 如动态规划，Dyna

决策时规划（Decision-time Planning）
• 规划只着眼于当前状态的动作选择
• 在不需要快速反应的应用中很有效，如棋类游戏

启发式搜索

  • 访问到当前状态(根节点)，对后续可能的情况进行树结构展开

  • 叶节点代表估计的值函数

  • 回溯到当前状态(根节点)，方式类似于值函数的更新方式
    在这里插入图片描述

  • 决策时规划，着重于当前状态

  • 贪婪策略在单步情况下的扩展

  • 启发式搜索看多步规划下，当前状态的最优行动

  • 搜索越深，计算量越大，得到的动作越接近最优

  • 性能提升不是源于多步更新，而是源于专注当前状态的后续可能

Rollout算法

  • 从当前状态进行模拟的蒙特卡洛估计
  • 选取最高估计值的动作
  • 在下一个状态重复上述步骤

特点

  • 决策时规划，从当前状态进行𝑟𝑜𝑙𝑙𝑜𝑢𝑡
  • 直接目的类似于策略迭代和改进，寻找更优的策略
  • 表现取决于蒙特卡洛方法估值的准确性

在这里插入图片描述

蒙特卡洛树搜索

在这里插入图片描述

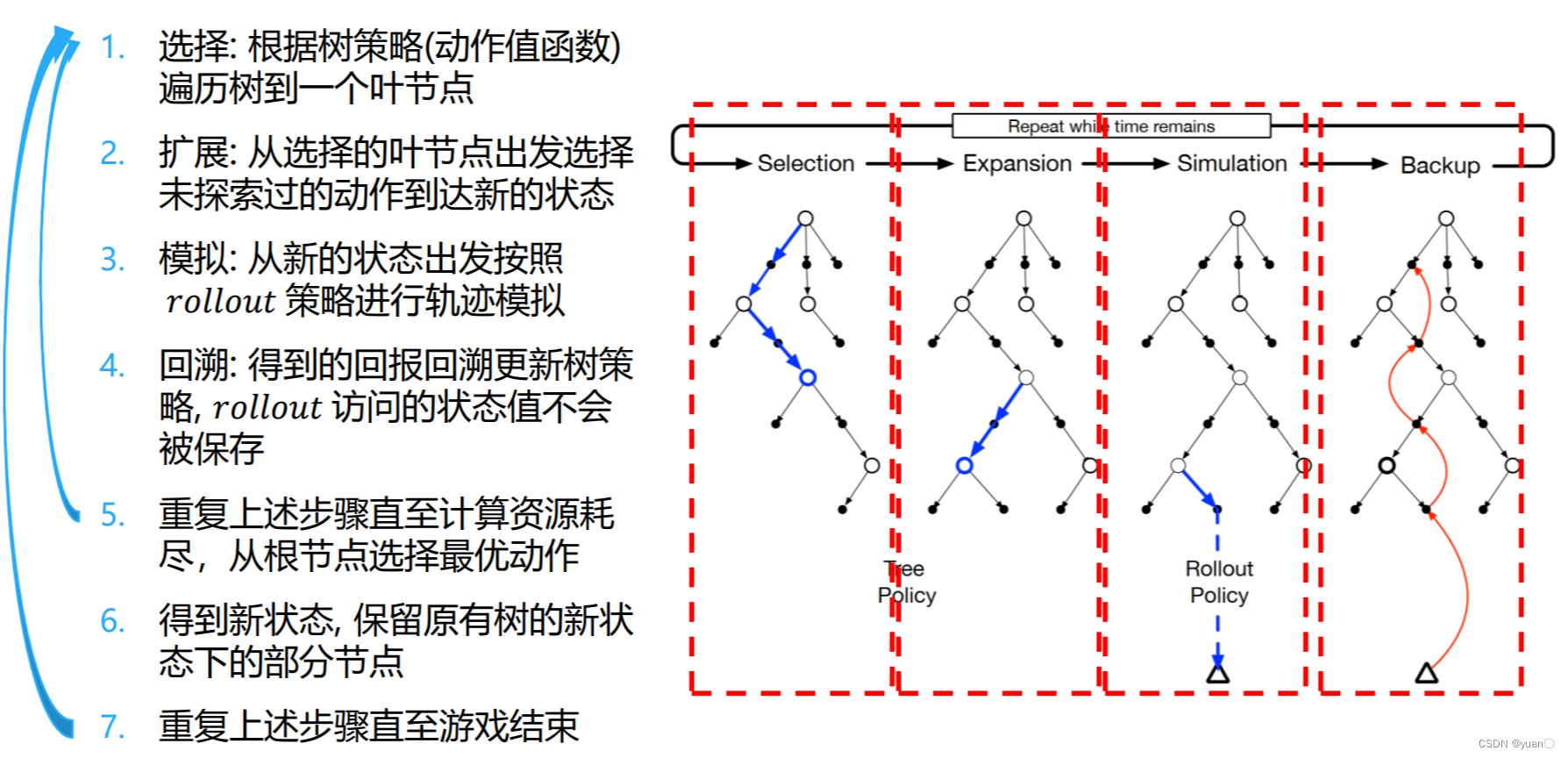
参考

[1] 伯禹AI
[2] https://www.deepmind.com/learning-resources/introduction-to-reinforcement-learning-with-david-silver
[3] 动手学强化学习
[4] Reinforcement Learning

相关文章：

【强化学习】08——规划与学习（采样方法|决策时规划）

文章目录 优先级采样Example1 Prioritized Sweepingon Mazes局限性及改进 期望更新和采样更新不同分支因子下的表现 轨迹采样总结实时动态规划Example2 racetrack 决策时规划启发式搜索Rollout算法蒙特卡洛树搜索 参考 先做个简单的笔记整理，以后有时间再补上细节 …...

编程日记 2023/10/27 4:08:25

(链表) 25. K 个一组翻转链表 ——【Leetcode每日一题】

❓ 25. K 个一组翻转链表 难度：困难 给你链表的头节点 head ，每 k 个节点一组进行翻转，请你返回修改后的链表。 k 是一个正整数，它的值小于或等于链表的长度。如果节点总数不是 k 的整数倍，那么请将最后剩余的节点保…...

编程日记 2023/10/27 4:06:22

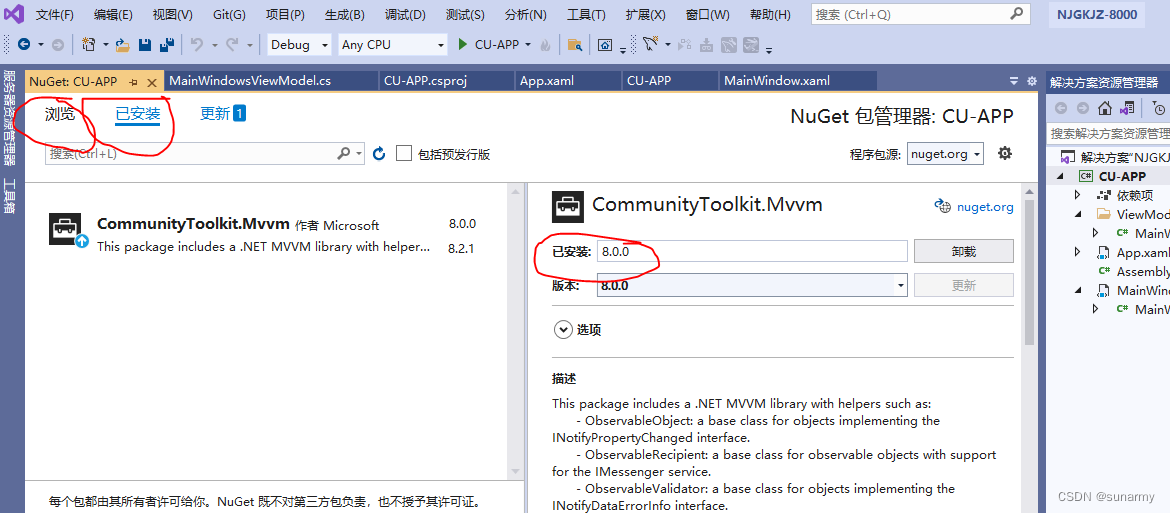
VisualStudio[WPF/.NET]基于CommunityToolkit.Mvvm架构开发

一、创建 "WPF应用程序" 新项目 项目模板选择如下&#xff1a; 暂时随机填一个目标框架&#xff0c;待会改&#xff1a; 二、修改“目标框架” 双击“解决方案资源管理器”中<项目>CU-APP, 打开<项目工程文件>CU-APP.csproj, 修改目标框架TargetFramew…...

编程日记 2023/10/27 4:05:21

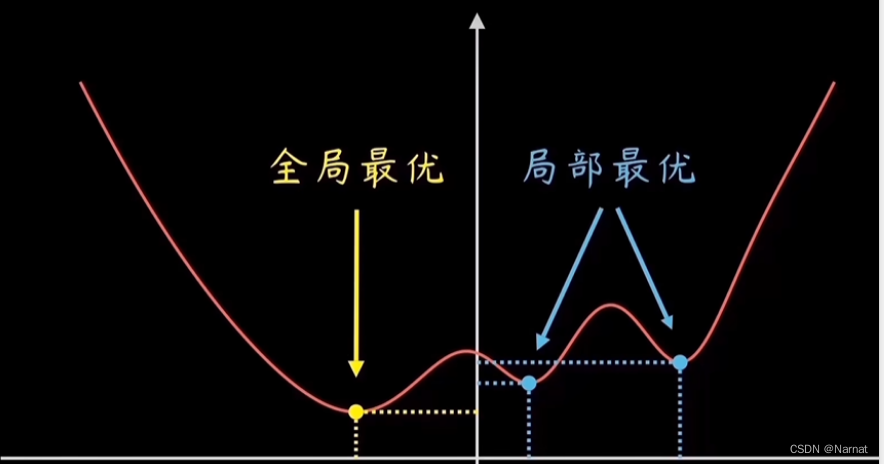
深度学习_5_模型拟合_梯度下降原理

需求: 想要找到一条直线&#xff0c;能更好的拟合这一些点 如何确定上述直线就是最优解呢&#xff1f; 由计算机算出所有点与我们拟合直线的误差&#xff0c;常见的是均方误差 例如&#xff1a;P1与直线之间的误差为e1 将P1坐标带入直线并求误差得&#xff1a; 推广到所有点&a…...

编程日记 2023/10/27 4:03:19

大模型时代，AI如何成为数实融合的驱动力？

10月25日&#xff0c;百度APP、百家号联合中兴通讯举办的“时代的增量“主题沙龙第二期在北京顺利召开。本期沙龙围绕“数实融合新视角”邀请学界、业界、媒体从业者等领域专家出席&#xff0c;以产学研相结合的视角深入探讨数实融合的最新技术趋势&#xff0c;并围绕数实融合在…...

编程日记 2023/10/27 4:02:17

MS COCO数据集的评价标准以及不同指标的选择推荐（AP、mAP、MS COCO、AR、@、0.5、0.75、1、目标检测、评价指标）

目标检测模型性能衡量指标、MS COCO 数据集的评价标准以及不同指标的选择推荐 0. 引言 0.1 COCO 数据集评价指标 目标检测模型通过 pycocotools 在验证集上会得到 COCO 的评价列表&#xff0c;具体参数的含义是什么呢&#xff1f; 0.2 目标检测领域常用的公开数据集 PASCAL …...

编程日记 2023/10/27 4:01:16

css实现鼠标多样化

cursor pointer&#xff1a; 手型default&#xff1a; 箭头text&#xff1a; 文本输入光标move&#xff1a; …...

编程日记 2023/10/27 4:00:15

21.2 Python 使用Scapy实现端口探测

Scapy 是一款使用纯Python编写的跨平台网络数据包操控工具&#xff0c;它能够处理和嗅探各种网络数据包。能够很容易的创建&#xff0c;发送&#xff0c;捕获&#xff0c;分析和操作网络数据包&#xff0c;包括TCP&#xff0c;UDP&#xff0c;ICMP等协议&#xff0c;此外它还提…...

编程日记 2023/10/27 3:59:14

Qt设计一个自定义的登录框窗口

今天写了一个Qt登录、注册的小demo&#xff0c;后续完善会连接MySQL使用&#xff0c;过几天写完我会放在github上。 主要页面&#xff1a; 动态演示&#xff1a; 写完这个界面后&#xff0c;我终于知道了Qt为什么几乎没什么好看的窗口设计了&#xff0c;随便写一个简单大方的登…...

编程日记 2023/10/27 3:58:13

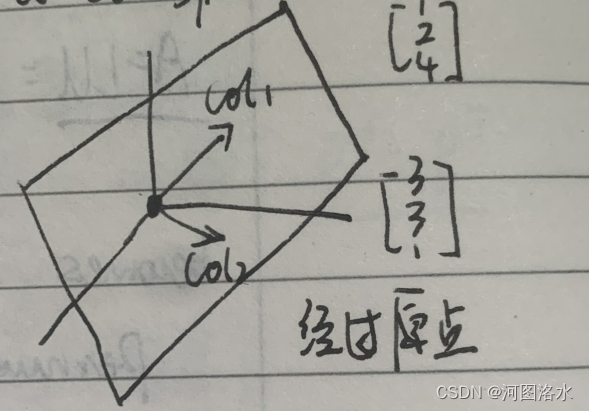
05 MIT线性代数-转置,置换,向量空间Transposes, permutations, spaces

1. Permutations P: execute row exchanges becomes PA LU for any invertible A Permutations P identity matrix with reordered rows mn (n-1) ... (3) (2) (1) counts recordings, counts all nxn permuations 对于nxn矩阵存在着n!个置换矩阵 , 2. Transpose: 2.…...

编程日记 2023/10/27 3:57:12

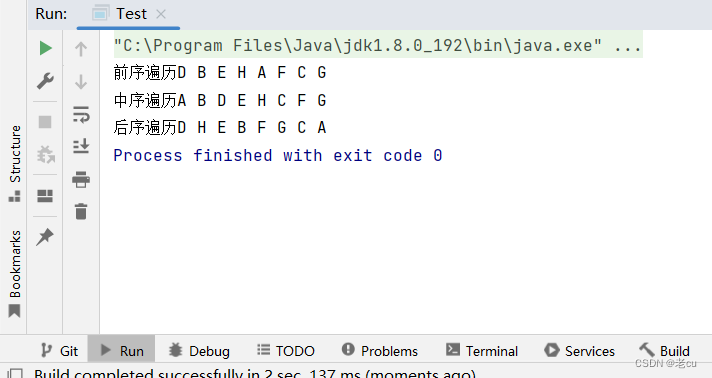
[数据结构】二叉树

1.概念 一棵二叉树是结点的一个有限集合&#xff0c;该集合&#xff1a; 1. 或者为空 2. 或者是由一个根节点加上两棵别称为左子树和右子树的二叉树组成 从上图我们可以发现&#xff1a; 1.二叉树不存在大于2 的度 2.二叉树的子树有左右之分&#xff0c;次序不能颠倒。是有…...

编程日记 2023/10/27 3:56:10

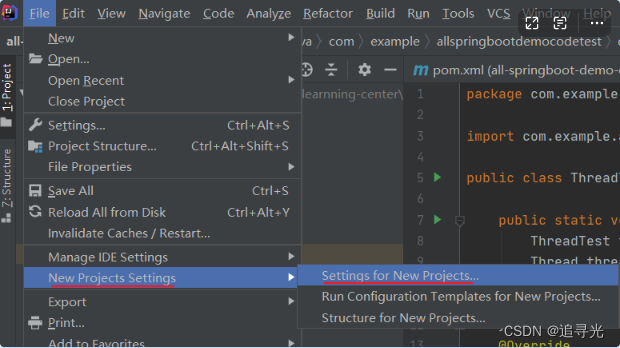
idea 中配置 maven

前文叙述&#xff1a; 配置 maven 一共要设置两个地方&#xff1a;1、为当前项目设置2、为新项目设置maven 的下载和安装可参考我之前写过的文章&#xff0c;具体的配置文章中也都有讲解。1、为当前项目进行 maven 配置 配置 VM Options: -DarchetypeCataloginternal2、为新项…...

编程日记 2023/10/27 3:55:09

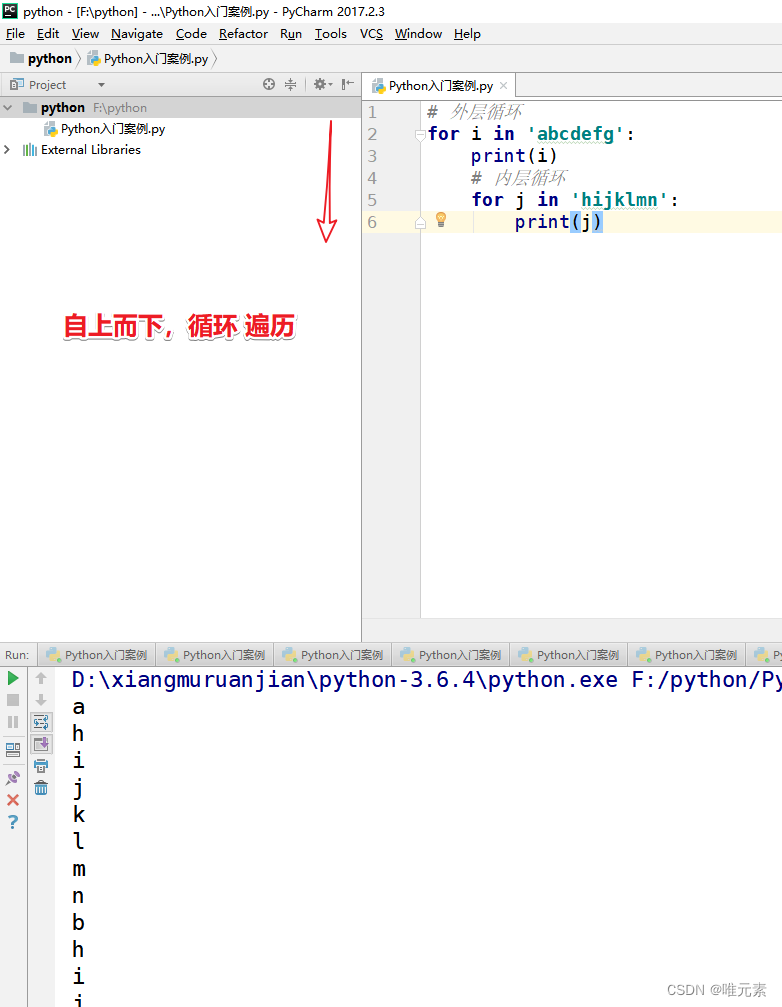
Python---for循环嵌套

for循环嵌套&#xff0c;就是一个for循环里面嵌套另外一个for循环的写法。 当循环结构相互嵌套时&#xff0c;位于外层的循环结构常简称为外层循环或外循环&#xff0c;位于内层的循环结构常简称为内层循环或内循环。 基本语法&#xff1a; # 外层循环 for i in 序列1:# 内层…...

编程日记 2023/10/27 3:54:08

189. 轮转数组 --力扣 --JAVA

题目 给定一个整数数组 nums&#xff0c;将数组中的元素向右轮转 k 个位置&#xff0c;其中 k 是非负数。 解题思路 通过位移后位置对数组长度的取余来判断元素变换后的位置 代码展示 class Solution {public void rotate(int[] nums, int k) {int size nums.length;int[]…...

编程日记 2023/10/27 3:53:07

C# 使用waveIn实现声音采集

文章目录 前言一、需要的对象及方法二、整体流程三、关键实现1、使用Thread开启线程2、TaskCompletionSource实现异步3、将指针封装为Stream 四、完整代码1.接口2.具体实现 五、使用示例方式一方式二 总结 前言 之前实现了《C 使用waveIn实现声音采集》&#xff0c;后来C#项目…...

编程日记 2023/10/27 3:51:05

长连接的原理

Apollo的长连接实现是 Spring的DeferredResult来实现的,先看怎么用 import ...RestController RequestMapping("deferredResult") public class DeferredResultController {private Map<String, Consumer<DeferredResultResponse>> taskMap new HashMa…...

编程日记 2023/10/27 3:50:05

软考系列（系统架构师）- 2015年系统架构师软考案例分析考点

试题一 软件架构&#xff08;质量属性效用树、架构风险、依够点、权衡点&#xff09; 【问题1】&#xff08;12分&#xff09; 在架构评估过程中&#xff0c;质量属性效用树&#xff08;utility tree&#xff09;是对系统质量属性进行识别和优先级排序的重要工具。请给出合适的…...

编程日记 2023/10/27 3:49:03

小程序开发——小程序的视图与渲染

1.视图与渲染过程 基本概念&#xff1a; 视图层由WXML页面文件和样式文件WXSS共同组成。事件是视图层和逻辑层沟通的纽带&#xff0c;用户操作触发事件后可通过同名的事件处理函数执行相应的逻辑&#xff0c;处理完成后&#xff0c;更新的数据又将再次渲染到页面上。 WXML页面…...

编程日记 2023/10/27 3:48:02

用python实现操作mongodb的插入和查找操作

用python实现操作mongodb的插入和查找操作 import pymongoclient pymongo.MongoClient("mongo://localhost:27017") db client["app"] col db["C1"]# 插入一条数据 #user { # "name": "Sam", # "age":…...

编程日记 2023/10/27 3:47:01

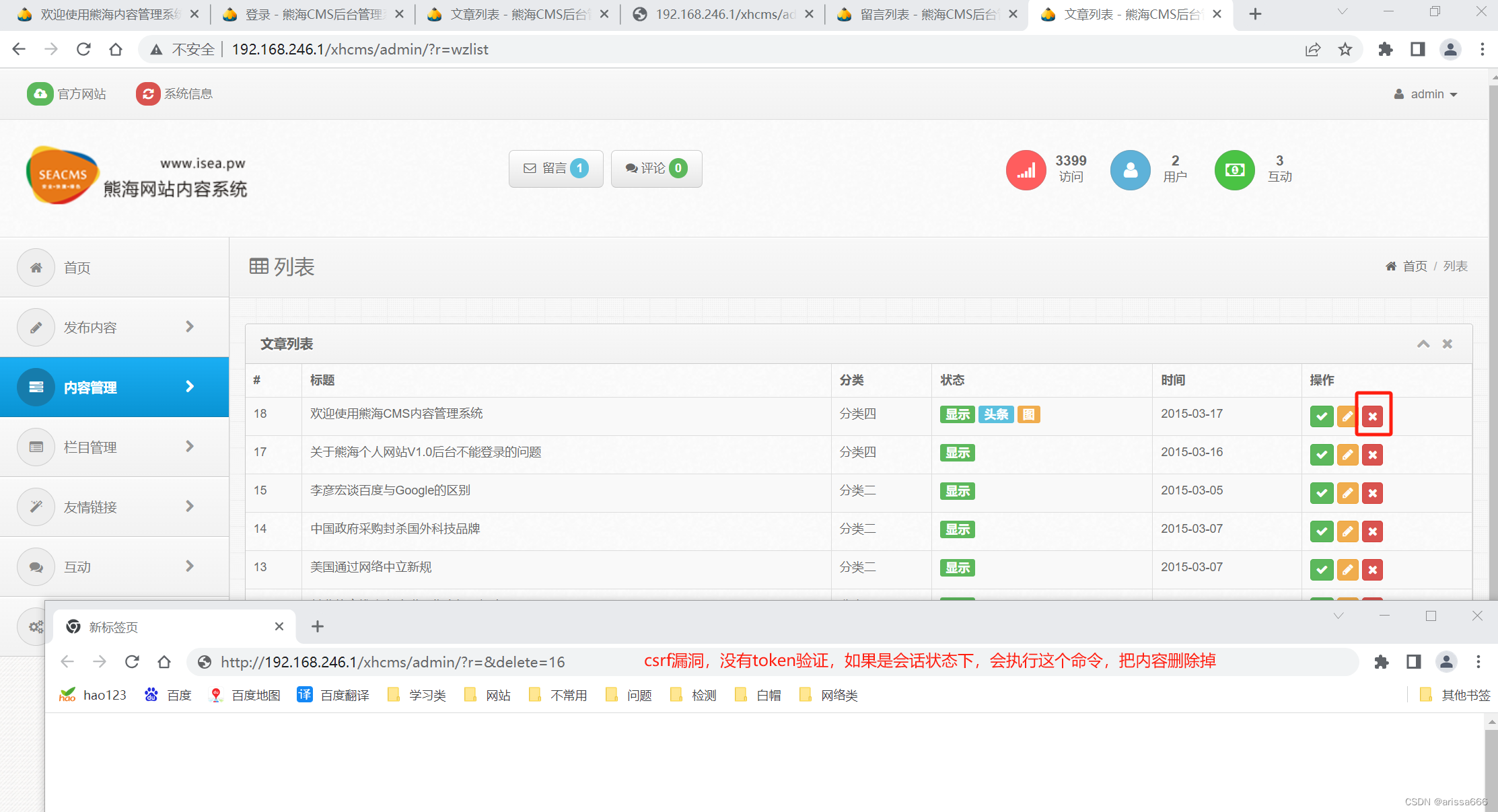
代码审计及示例

简介&#xff1a; 代码安全测试是从安全的角度对代码进行的安全测试评估。 结合丰富的安全知识、编程经验、测试技术&#xff0c;利用静态分析和人工审核的方法寻找代码在架构和编码上的安全缺陷&#xff0c;在代码形成软件产品前将业务软件的安全风险降到最低。 方法&#x…...

编程日记 2023/10/27 3:46:00

Linux应用开发之网络套接字编程(实例篇)

服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

编程新知 2025/9/20 0:09:23

通过Wrangler CLI在worker中创建数据库和表

官方使用文档&#xff1a;Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后&#xff0c;会在本地和远程创建数据库&#xff1a; npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库&#xff1a; 现在&#xff0c;您的Cloudfla…...

编程新知 2025/9/20 0:21:45

在四层代理中还原真实客户端ngx_stream_realip_module

一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡&#xff08;如 HAProxy、AWS NLB、阿里 SLB&#xff09;发起上游连接时&#xff0c;将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后&#xff0c;ngx_stream_realip_module 从中提取原始信息…...

编程新知 2025/8/4 15:55:44

【配置 YOLOX 用于按目录分类的图片数据集】

现在的图标点选越来越多&#xff0c;如何一步解决&#xff0c;采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集&#xff08;每个目录代表一个类别&#xff0c;目录下是该类别的所有图片&#xff09;&#xff0c;你需要进行以下配置步骤&#x…...

编程新知 2025/9/16 7:41:25

算法岗面试经验分享-大模型篇

文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer &#xff08;1&#xff09;资源 论文&a…...

编程新知 2025/9/18 12:53:33

脑机新手指南（七）：OpenBCI_GUI：从环境搭建到数据可视化（上）

一、OpenBCI_GUI 项目概述 &#xff08;一&#xff09;项目背景与目标 OpenBCI 是一个开源的脑电信号采集硬件平台&#xff0c;其配套的 OpenBCI_GUI 则是专为该硬件设计的图形化界面工具。对于研究人员、开发者和学生而言&#xff0c;首次接触 OpenBCI 设备时&#xff0c;往…...

编程新知 2025/9/2 16:55:16

mac：大模型系列测试

0 MAC 前几天经过学生优惠以及国补17K入手了mac studio,然后这两天亲自测试其模型行运用能力如何&#xff0c;是否支持微调、推理速度等能力。下面进入正文。 1 mac 与 unsloth 按照下面的进行安装以及测试&#xff0c;是可以跑通文章里面的代码。训练速度也是很快的。 注意…...

编程新知 2025/9/20 22:54:35

使用SSE解决获取状态不一致问题

使用SSE解决获取状态不一致问题 1. 问题描述2. SSE介绍2.1 SSE 的工作原理2.2 SSE 的事件格式规范2.3 SSE与其他技术对比2.4 SSE 的优缺点 3. 实战代码 1. 问题描述 目前做的一个功能是上传多个文件&#xff0c;这个上传文件是整体功能的一部分&#xff0c;文件在上传的过程中…...

编程新知 2025/9/11 19:15:10

文件上传漏洞防御全攻略

要全面防范文件上传漏洞&#xff0c;需构建多层防御体系&#xff0c;结合技术验证、存储隔离与权限控制&#xff1a; &#x1f512; 一、基础防护层 前端校验&#xff08;仅辅助&#xff09; 通过JavaScript限制文件后缀名&#xff08;白名单&#xff09;和大小&#xff0c;提…...

编程新知 2025/8/18 19:05:00

高分辨率图像合成归一化流扩展

大家读完觉得有帮助记得关注和点赞&#xff01;&#xff01;&#xff01; 1 摘要 我们提出了STARFlow&#xff0c;一种基于归一化流的可扩展生成模型&#xff0c;它在高分辨率图像合成方面取得了强大的性能。STARFlow的主要构建块是Transformer自回归流&#xff08;TARFlow&am…...

编程新知 2025/9/13 17:33:14