当前位置： 首页 > news >正文

STM32 音频ADC转wav格式

news 2025/9/20 20:52:36

STM32 音频ADC DAC测试方法_stm32 adc 音频-CSDN博客

STM32--vs1053 WAV录音实现（保存在SD卡）_vs1053 多字节读取-CSDN博客

单片机内部AD实现录音wav文件_adc语音信号采样_天外飞仙CUG的博客-CSDN博客

PCM编码格式_pcm格式-CSDN博客

用ADC编码PCM数据录制WAV格式音频文件-CSDN博客

stm32f103+FFT+OLED的音乐频谱制作（只需三步即可）_stm32 音乐频谱-CSDN博客

STM32F103 WAV录音SD存储 WAV语音软解播放_stm32f103 软解歌曲-CSDN博客

STM32之音乐播放器_stm32音乐播放器_IT_阿水的博客-CSDN博客

用ADC编码PCM数据录制WAV格式音频文件-CSDN博客

wav文件格式分析与详解

WAV 音频文件解读和分析_宁静致远的技术博客_51CTO博客

WAV文件的频谱图显示——总结篇_wav文件画频谱图-CSDN博客

【精选】wav音频文件的提取和分析(matlab)_matlab怎么读取wav音频文件-CSDN博客

基于Python的热门音乐特征数据分析 - 知乎

音频特征值提取笔记_MATLAB在语音信号分析与合成中应用-CSDN博客

.wav音频提取软件

如何进行音频提取？这5款软件必备！
https://baijiahao.baidu.com/s?id=1772443781693434997&wfr=spider&for=pc

相关文章：

STM32 音频ADC转wav格式

STM32 音频ADC DAC测试方法_stm32 adc 音频-CSDN博客 STM32--vs1053 WAV录音实现（保存在SD卡）_vs1053 多字节读取-CSDN博客 单片机内部AD实现录音wav文件_adc语音信号采样_天外飞仙CUG的博客-CSDN博客 PCM编码格式_pcm格式-CSDN博客 用ADC编码PCM数据…...

编程日记 2023/10/27 4:39:05

面试中经常问道的问题二

深入理解前端跨域方法和原理 前言 受浏览器同源策略的限制，本域的js不能操作其他域的页面对象（比如DOM）。但在安全限制的同时也给注入iframe或是ajax应用上带来了不少麻烦。所以我们要通过一些方法使本域的js能够操作其他域的页面对象或者使…...

编程日记 2023/10/27 4:38:03

SQL UPDATE 语句（更新表中的记录）

SQL UPDATE 语句 UPDATE 语句用于更新表中已存在的记录。 还可以使用AND或OR运算符组合多个条件。 SQL UPDATE 语法 具有WHERE子句的UPDATE查询的基本语法如下所示： UPDATE table_name SET column1 value1, column2 value2, ... WHERE conditi…...

编程日记 2023/10/27 4:37:02

js节流和防抖

节流（throttle）和防抖（debounce）是为了解决函数频繁触发而引发性能问题的两种优化方法。 节流： 指定一个时间间隔，在时间间隔内只执行一次函数，即在一段时间内，多次触发函数只执行一…...

编程日记 2023/10/27 4:36:01

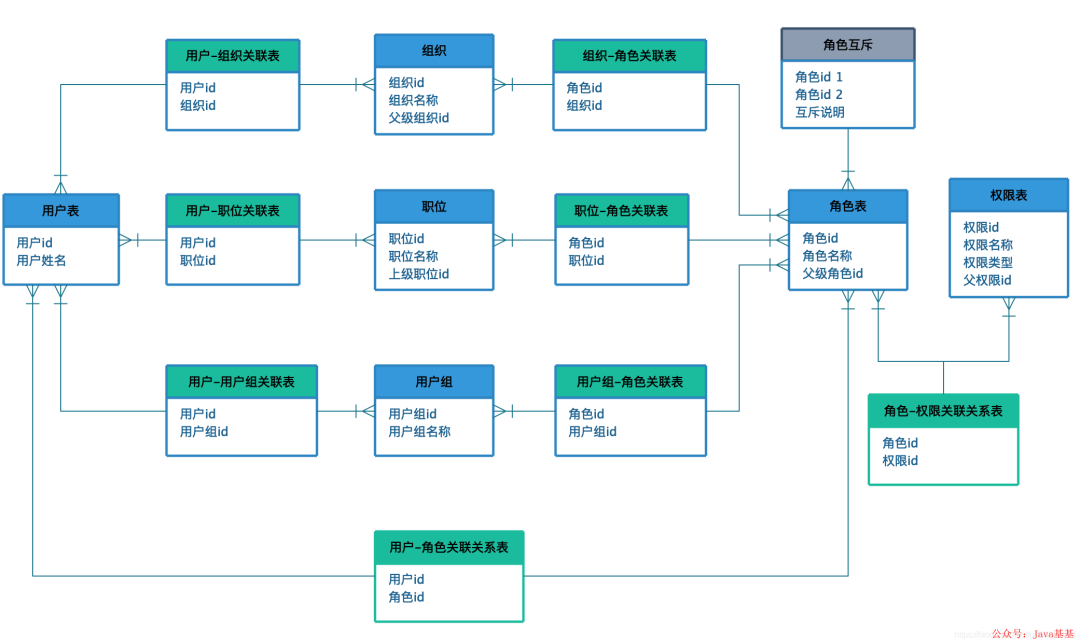
权限系统设计(转载)

1 为什么需要权限管理 2 权限模型 2.1 权限设计 2.2 为什么需要角色 2.3 权限模型的演进 2.4 用户划分 2.5 理想的RBAC模型 3 权限系统表设计 3.1 标准RBAC模型表设计 3.2 理想RBAC模型表设计 4 结语 1 为什么需要权限管理 日常工作中权限的问题时时刻刻伴随着我们&a…...

编程日记 2023/10/27 4:35:00

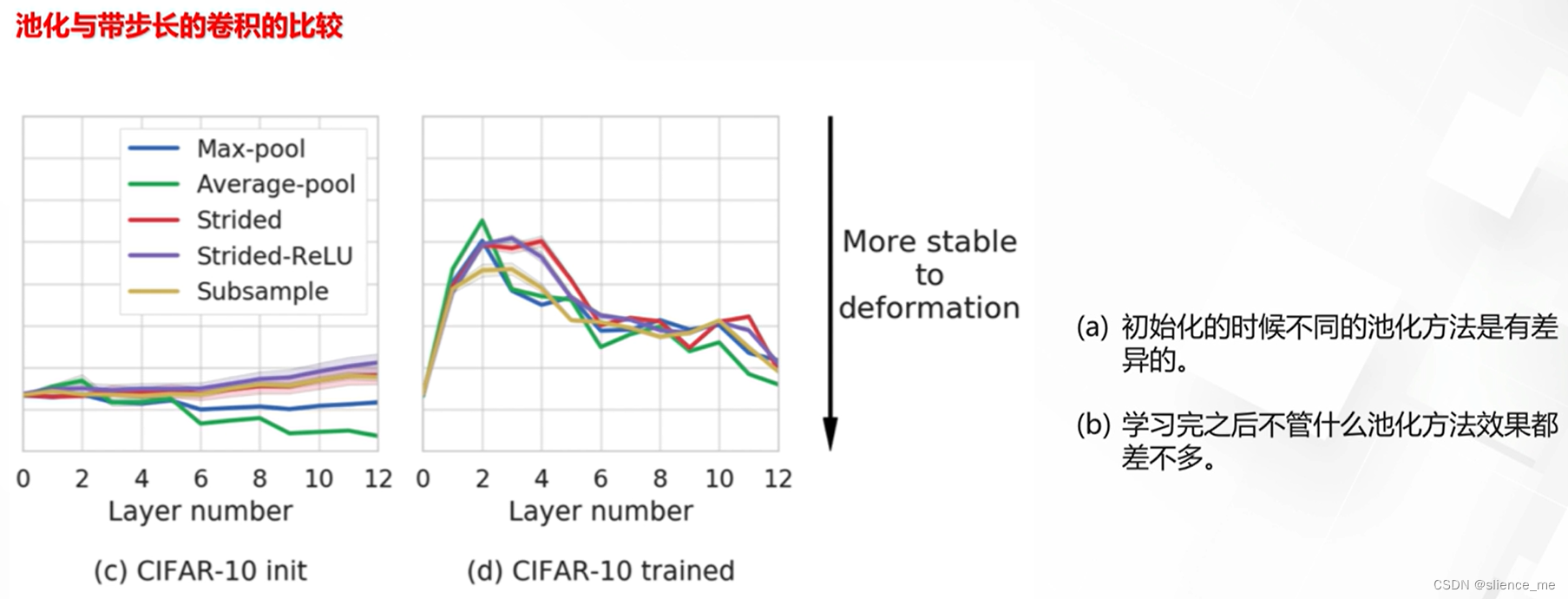
【机器学习合集】标准化与池化合集 -＞（个人学习记录笔记）

文章目录 标准化与池化1. 标准化/归一化1.1 归一化归一化的作用 1.2 标准化批标准化方法 Batch Normailzation标准化方法的对比自动学习标准化方法 2. 池化2.1 池化的作用2.2 常见的池化方法2.3 池化方法的差异2.4 池化的必要性 标准化与池化 1. 标准化/归一化 1.1 归一化 归…...

编程日记 2023/10/27 4:32:57

Dockerfile文件自动化生成R4L镜像

Dockerfile文件自动化生成R4L镜像的步骤 1、安装Docker：2、使用Dockerfile一键生成镜像：3、查看生成的Docker镜像：4、删除Docker镜像：5、生成Docker容器：6、查看容器7、删除容器 1、安装Docker： curl -fsS…...

编程日记 2023/10/27 4:30:55

基于SSM的居家养老系统

末尾获取源码 开发语言：Java Java开发工具：JDK1.8 后端框架：SSM 前端：Vue 数据库：MySQL5.7和Navicat管理工具结合 服务器：Tomcat8.5 开发软件：IDEA / Eclipse 是否Maven项目：是 目录…...

编程日记 2023/10/27 4:29:54

[C#基础训练]FoodRobot食品管理部分代码-2

参考代码： using System; using System.Collections.Generic;namespace FoodRobotDemo {public class FoodInfo{ public string Name { get; set; } public int Id { get; set; } public int Count { get; set; }}public class FoodRobot{private …...

编程日记 2023/10/27 4:28:53

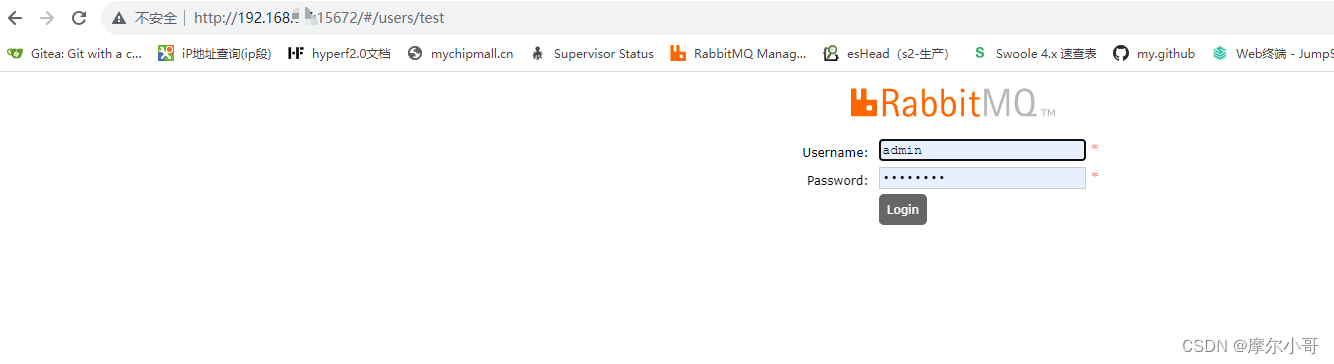
docker部署rabbitmq的坑

背景 今天用docker部署rabbitmq，启动都一起正常，但是当访问15672端口时，不能加载出页面。 排查 1.防火墙是否开启 ufw status2.ip是否能ping通 ping 192.168.x.x3.检查docker日志 docker psdocker logs -f 容器id4.进入容器&#xff0c…...

编程日记 2023/10/27 4:27:52

【python VS vba(系列2)】 python和vba读写EXCEL文件的方式比较 （建设ing）

目录 1 用VBA读写EXCEL文件 1.1 用VBA读写，本工作簿workbook里的特定sheet的特定内容 1.1.1 EXCEL表内内容访问 1.1.2 注意点 1.1.3 代码 1.2 用VBA读写本工作簿workbook里的所有sheet的内容 1.2.1 麻烦之处 1.2.2 方法，如何指定EXCEL里的内容…...

编程日记 2023/10/27 4:26:51

小程序 swiper滑动 层叠滑动效果

整个红色区域为可滑动区域&#xff0c;数字1区域为展示区域&#xff0c;数字2为下一个展示模块 <scroll-view class"h_scroll_horizontal" enhanced"ture" bind:touchend"touchEnd" bind:touchstart"touchStart"><view clas…...

编程日记 2023/10/27 4:23:47

【20年VIO梳理】

19-20年VIO 梳理 1. 开源代码介绍&#xff1a; DSM2. FMD Stereo SLAM&#xff1a;融合MVG和直接方法&#xff0c;实现准确&#xff0c;快速的双目SLAM3. 基于VINS-Mono开发的SPVIS4. 改进&#xff1a;一种基于光流的动态环境移动机器人定位方案5. PVIO:基于先验平面约束的高效…...

编程日记 2023/10/27 4:22:45

Java Object类详解

Object 是 java 类库中的一个特殊类&#xff0c;也是所有类的父类。也就是说&#xff0c;Java 允许把任何类型的对象赋给 Object 类型的变量。当一个类被定义后&#xff0c;如果没有指定继承的父类&#xff0c;那么默认父类就是 Object 类。因此&#xff0c;以下两个类表示的含…...

编程日记 2023/10/27 4:21:43

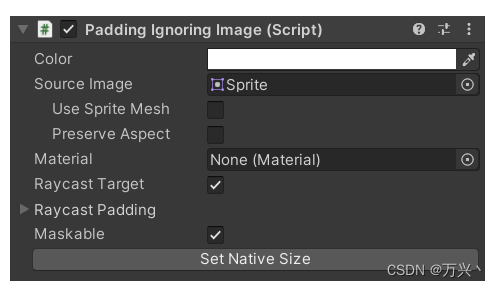
Unity 中忽略图片透明度的 Image 组件的修改版本

只需将此组件添加到画布中的空对象即可。请注意&#xff0c;仅支持简单 图像类型。 using System.Collections.Generic; using UnityEngine; using UnityEngine.Sprites; using UnityEngine.UI; #if UNITY_2017_4 || UNITY_2018_2_OR_NEWER using UnityEngine.U2D; #endif#if U…...

编程日记 2023/10/27 4:20:42

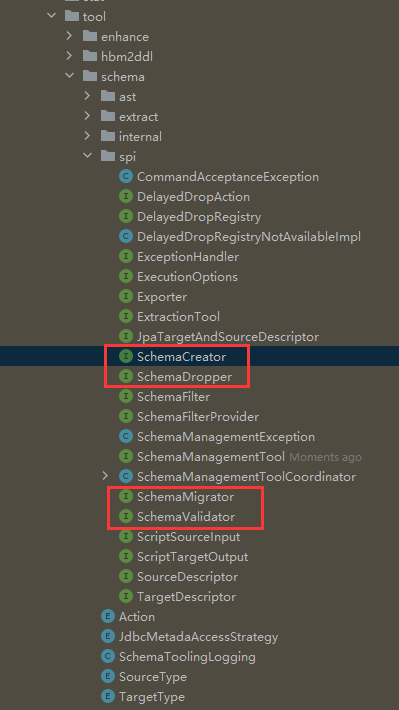
hibernate源码（1）--- schema创建

sessionFactory 配置项&#xff1a; hibernate的核心是sessionFactory&#xff0c;那我们看看如何构建session Factory。 参考官网&#xff1a; plugins {id("java") } group "com.atai.hibernatespy" version "1.0-SNAPSHOT" repositories…...

编程日记 2023/10/27 4:19:41

数学与经济管理

数学与经济管理&#xff08;2-4分&#xff09; 章节概述 最小生成树问题 答案&#xff1a;23 讲解地址&#xff1a;74-最小生成树问题_哔哩哔哩_bilibili 最短路径问题 答案&#xff1a;81 讲解地址&#xff1a;75-最短路径问题_哔哩哔哩_bilibili 网络与最大流量问题 真题 讲解…...

编程日记 2023/10/27 4:18:40

自动化测试系列 —— UI自动化测试

UI 测试是一种测试类型&#xff0c;也称为用户界面测试&#xff0c;通过该测试&#xff0c;我们检查应用程序的界面是否工作正常或是否存在任何妨碍用户行为且不符合书面规格的 BUG。了解用户将如何在用户和网站之间进行交互以执行 UI 测试至关重要&#xff0c;通过执行 UI 测试…...

编程日记 2023/10/27 4:17:39

眨个眼就学会了PixiJS

本文简介 带尬猴&#xff0c;我是德育处主任 当今的Web开发中&#xff0c;图形和动画已经成为了吸引用户注意力的重要手段之一。而 Pixi.js 作为一款高效、易用的2D渲染引擎&#xff0c;已经成为了许多开发者的首选&#xff08;我吹的&#xff09;。本文将为工友们介绍PixiJS的…...

编程日记 2023/10/27 4:16:38

WORD中的表格内容回车行距过大无法调整行距

word插入表格&#xff0c;编辑内容&#xff0c;换行遇到如下问题&#xff1a; 回车后行距过大&#xff0c;无法调整行距。 解决方法&#xff08;并行&#xff09;&#xff1a; 方法1&#xff1a;选中要调整的内容&#xff0c;菜单路径&#xff1a;“编辑-清除-格式” 方法2&am…...

编程日记 2023/10/27 4:13:31

Docker 离线安装指南

参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性&#xff0c;不同版本的Docker对内核版本有不同要求。例如&#xff0c;Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本&#xff0c;Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

编程新知 2025/9/20 17:07:55

7.4.分块查找

一.分块查找的算法思想&#xff1a; 1.实例&#xff1a; 以上述图片的顺序表为例&#xff0c; 该顺序表的数据元素从整体来看是乱序的&#xff0c;但如果把这些数据元素分成一块一块的小区间&#xff0c; 第一个区间[0,1]索引上的数据元素都是小于等于10的&#xff0c; 第二…...

编程新知 2025/9/18 0:10:03

脑机新手指南（八）：OpenBCI_GUI：从环境搭建到数据可视化（下）

一、数据处理与分析实战 &#xff08;一&#xff09;实时滤波与参数调整 基础滤波操作 60Hz 工频滤波&#xff1a;勾选界面右侧 “60Hz” 复选框&#xff0c;可有效抑制电网干扰&#xff08;适用于北美地区&#xff0c;欧洲用户可调整为 50Hz&#xff09;。 平滑处理&…...

编程新知 2025/7/31 5:34:43

React Native 导航系统实战（React Navigation）

导航系统实战&#xff08;React Navigation&#xff09; React Navigation 是 React Native 应用中最常用的导航库之一&#xff0c;它提供了多种导航模式&#xff0c;如堆栈导航&#xff08;Stack Navigator&#xff09;、标签导航&#xff08;Tab Navigator&#xff09;和抽屉…...

编程新知 2025/9/17 21:33:42

学校招生小程序源码介绍

基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码&#xff0c;专为学校招生场景量身打造&#xff0c;功能实用且操作便捷。 从技术架构来看&#xff0c;ThinkPHP提供稳定可靠的后台服务&#xff0c;FastAdmin加速开发流程&#xff0c;UniApp则保障小程序在多端有良好的兼…...

编程新知 2025/9/14 12:35:09

智能分布式爬虫的数据处理流水线优化：基于深度强化学习的数据质量控制

在数字化浪潮席卷全球的今天&#xff0c;数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具&#xff0c;在大规模数据获取中发挥着关键作用。然而&#xff0c;传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时&#xff0c;常出现数据质…...

编程新知 2025/9/7 8:50:57

【JVM面试篇】高频八股汇总——类加载和类加载器

目录 1. 讲一下类加载过程&#xff1f; 2. Java创建对象的过程&#xff1f; 3. 对象的生命周期&#xff1f; 4. 类加载器有哪些&#xff1f; 5. 双亲委派模型的作用&#xff08;好处&#xff09;&#xff1f; 6. 讲一下类的加载和双亲委派原则&#xff1f; 7. 双亲委派模…...

编程新知 2025/9/4 14:20:38

scikit-learn机器学习

# 同时添加如下代码, 这样每次环境(kernel)启动的时候只要运行下方代码即可: # Also add the following code, # so that every time the environment (kernel) starts, # just run the following code: import sys sys.path.append(/home/aistudio/external-libraries)机…...

编程新知 2025/7/5 19:39:42

微服务通信安全：深入解析mTLS的原理与实践

&#x1f525;「炎码工坊」技术弹药已装填&#xff01; 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、引言&#xff1a;微服务时代的通信安全挑战 随着云原生和微服务架构的普及&#xff0c;服务间的通信安全成为系统设计的核心议题。传统的单体架构中&…...

编程新知 2025/7/6 17:40:31

多元隐函数 偏导公式

我们来推导隐函数 z z ( x , y ) z z(x, y) zz(x,y) 的偏导公式&#xff0c;给定一个隐函数关系&#xff1a; F ( x , y , z ( x , y ) ) 0 F(x, y, z(x, y)) 0 F(x,y,z(x,y))0 &#x1f9e0; 目标&#xff1a; 求 ∂ z ∂ x \frac{\partial z}{\partial x} ∂x∂z​、 …...

编程新知 2025/9/19 5:31:38