数学与经济管理
数学与经济管理(2-4分)
章节概述

最小生成树问题
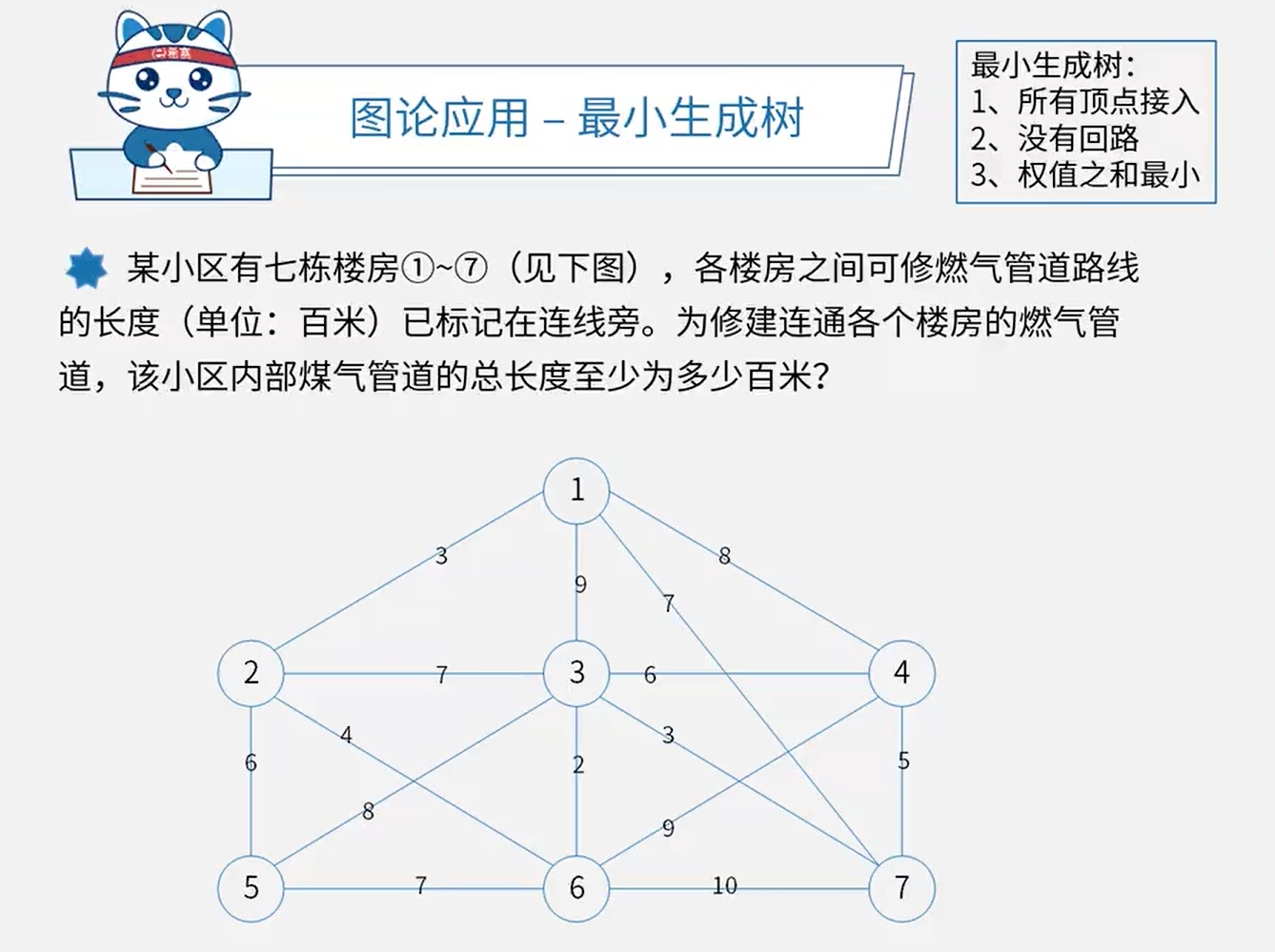
答案:23
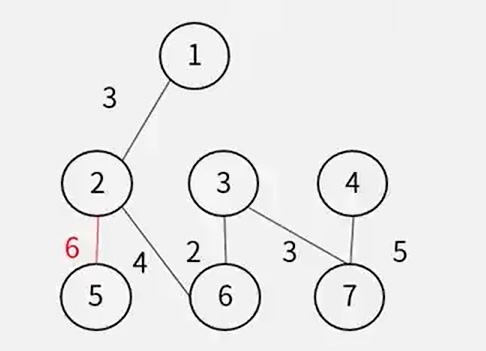
讲解地址:74-最小生成树问题_哔哩哔哩_bilibili
最短路径问题

答案:81
讲解地址:75-最短路径问题_哔哩哔哩_bilibili
网络与最大流量问题
真题

讲解地址:76-网络与最大流量问题_哔哩哔哩_bilibili
真题
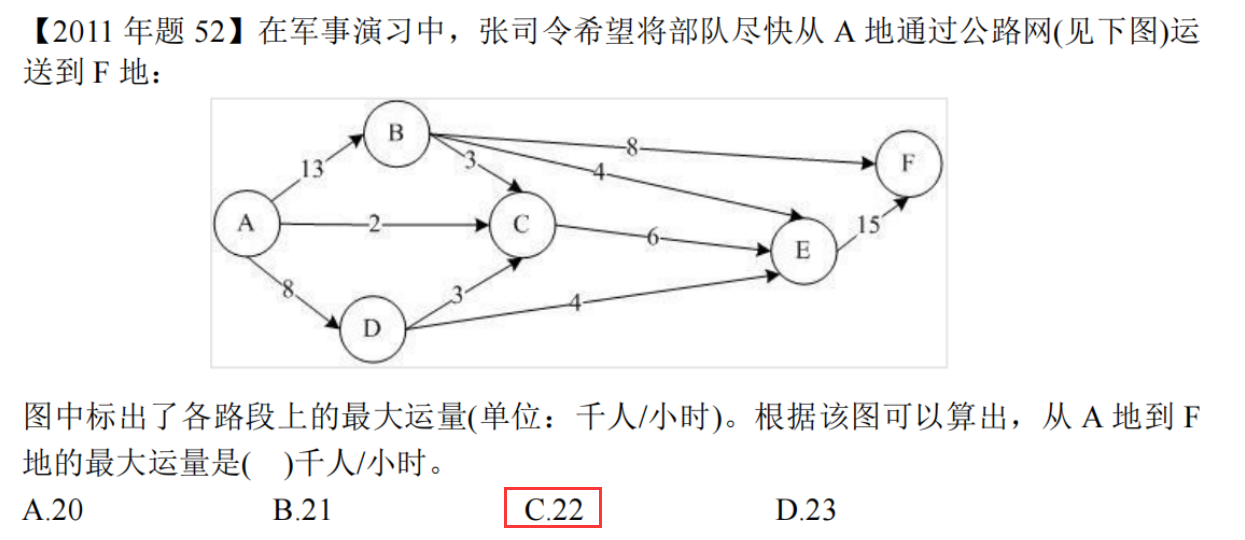

讲解地址:76-网络与最大流量问题_哔哩哔哩_bilibili
线性规划
真题


真题
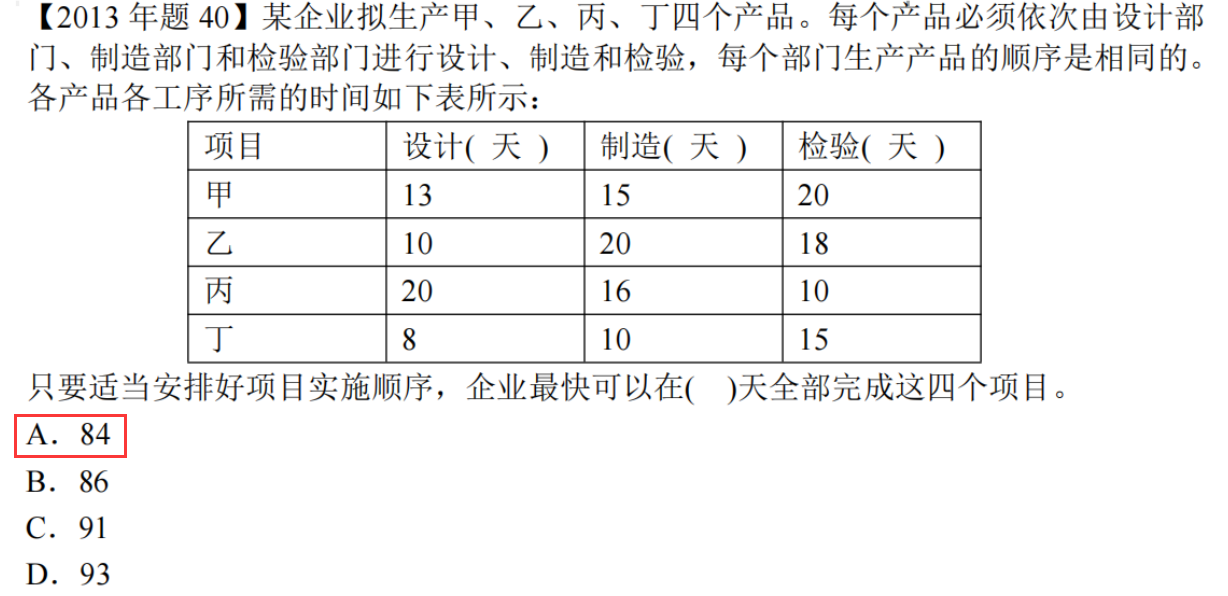

真题
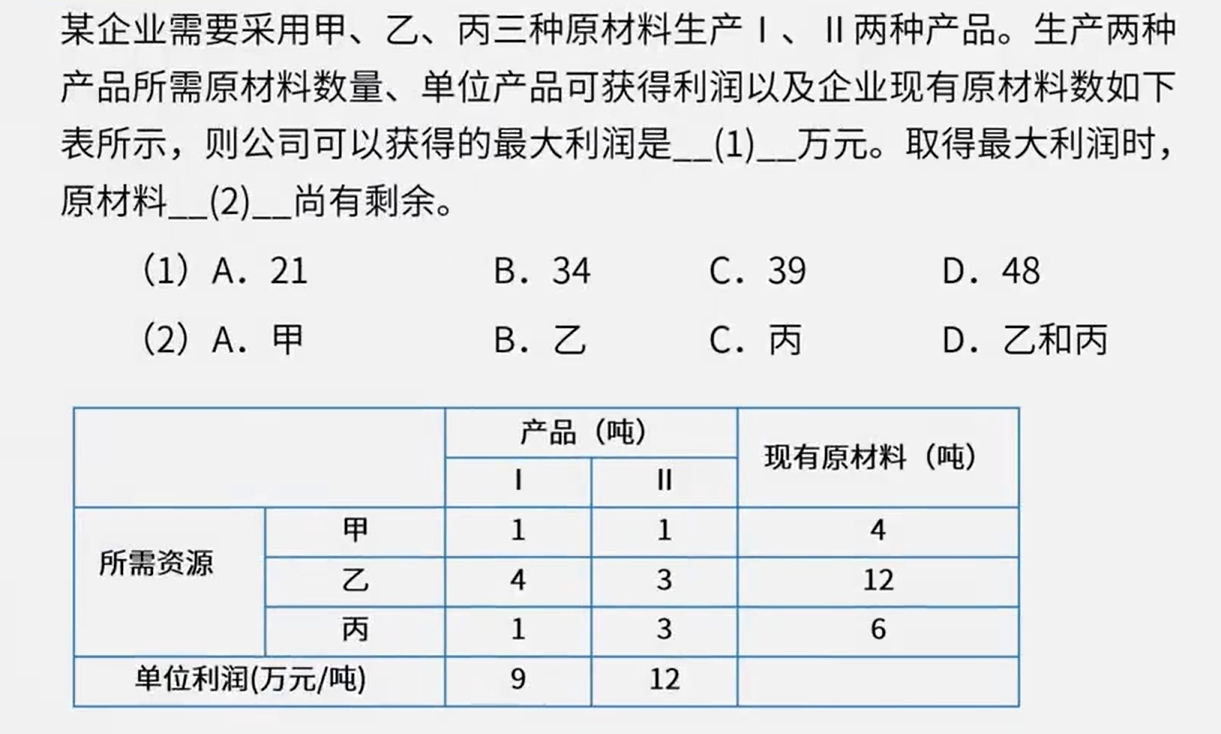
讲解地址:77-线性规划_哔哩哔哩_bilibili
真题
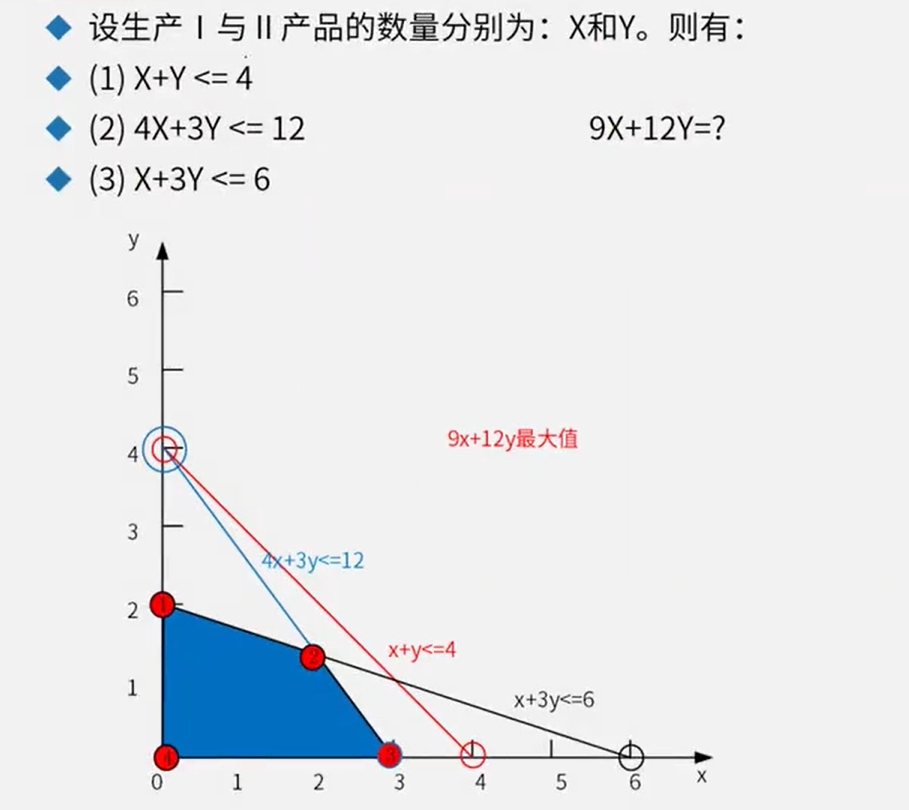
答案:34
真题


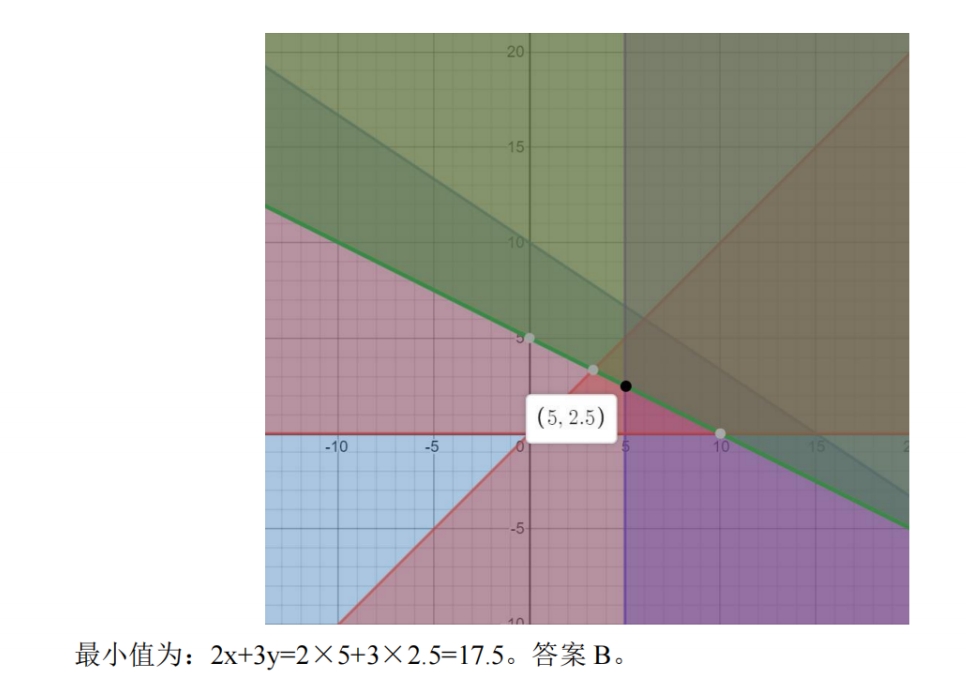
暴力出奇迹(动态规划)
真题
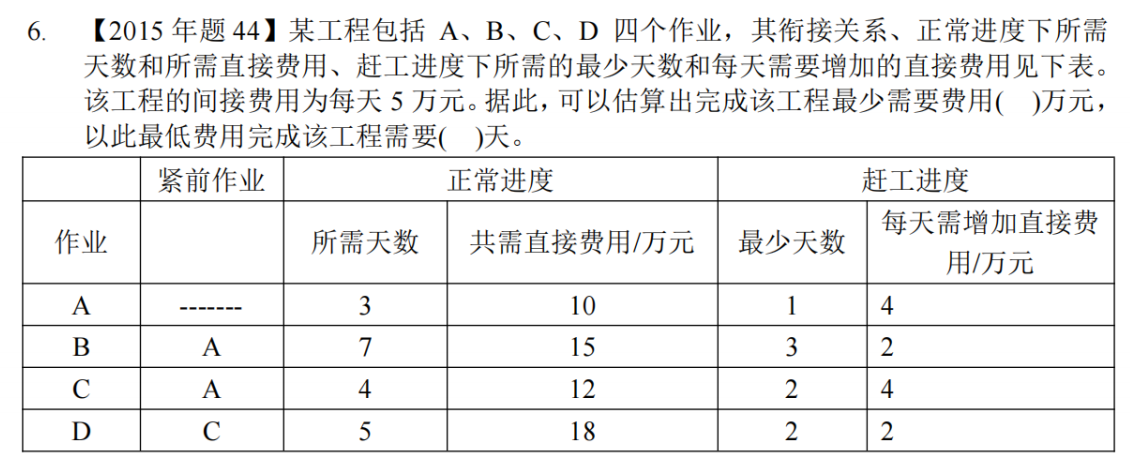
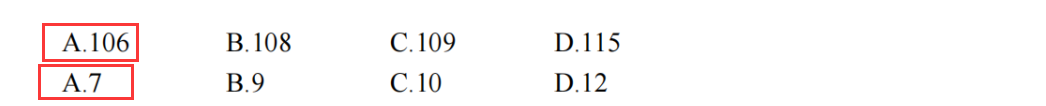
真题
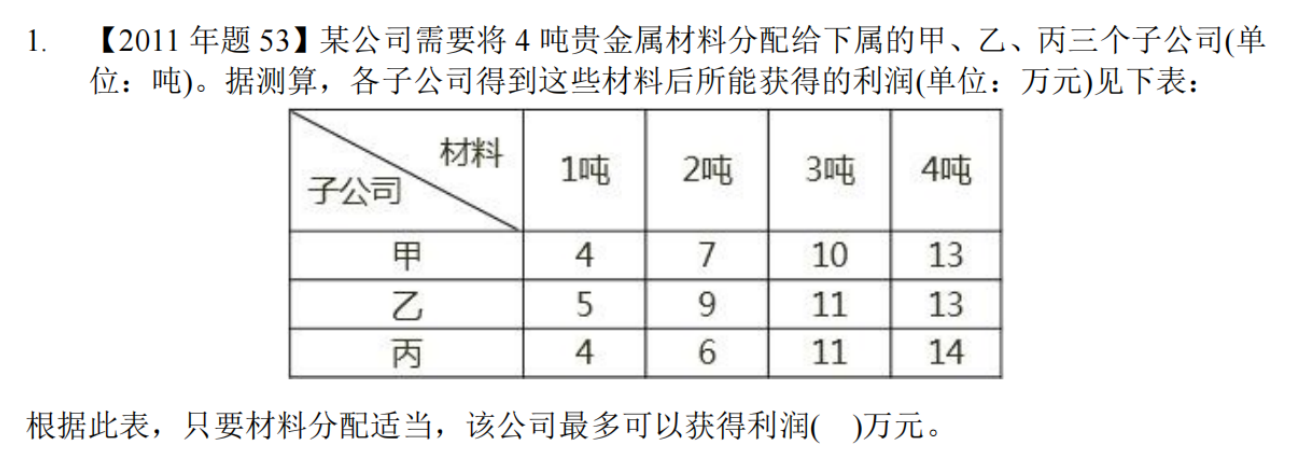
答案:17万


骚戴理解:这里我用的穷举法,一个个列出来,这个方法是最笨最容易出错的,但是是最简单的方法,同时注意在穷举的时候融入控制变量法的思想
真题
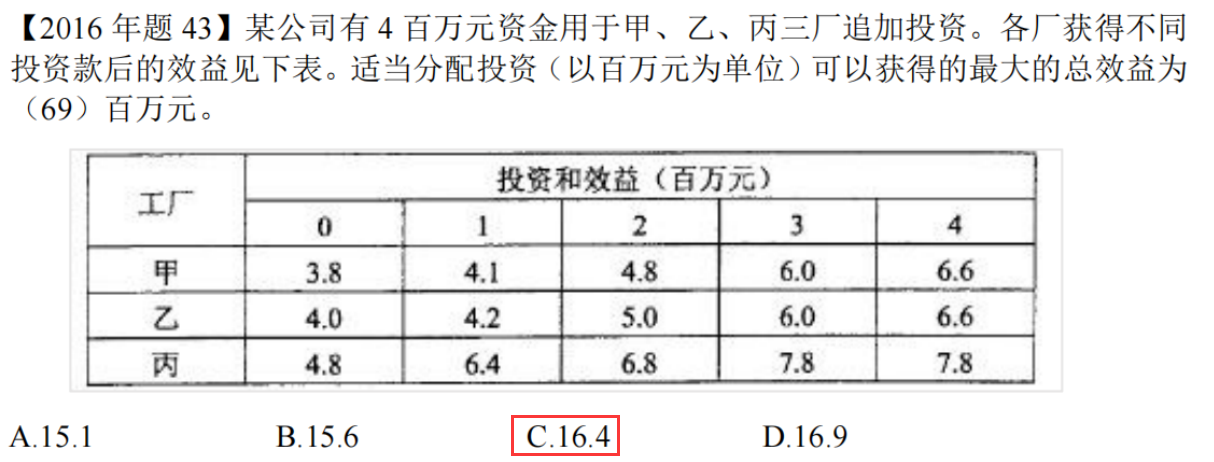
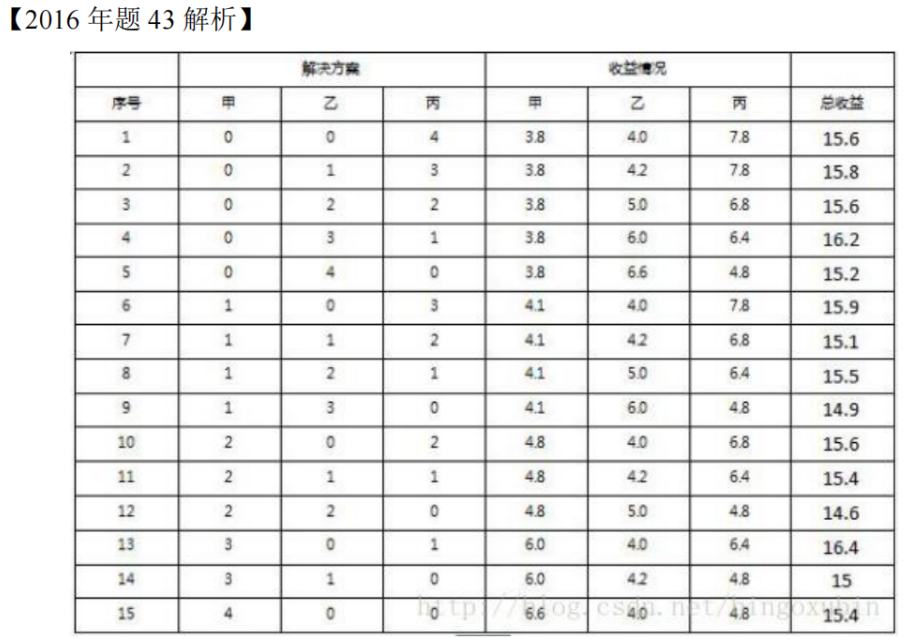
真题
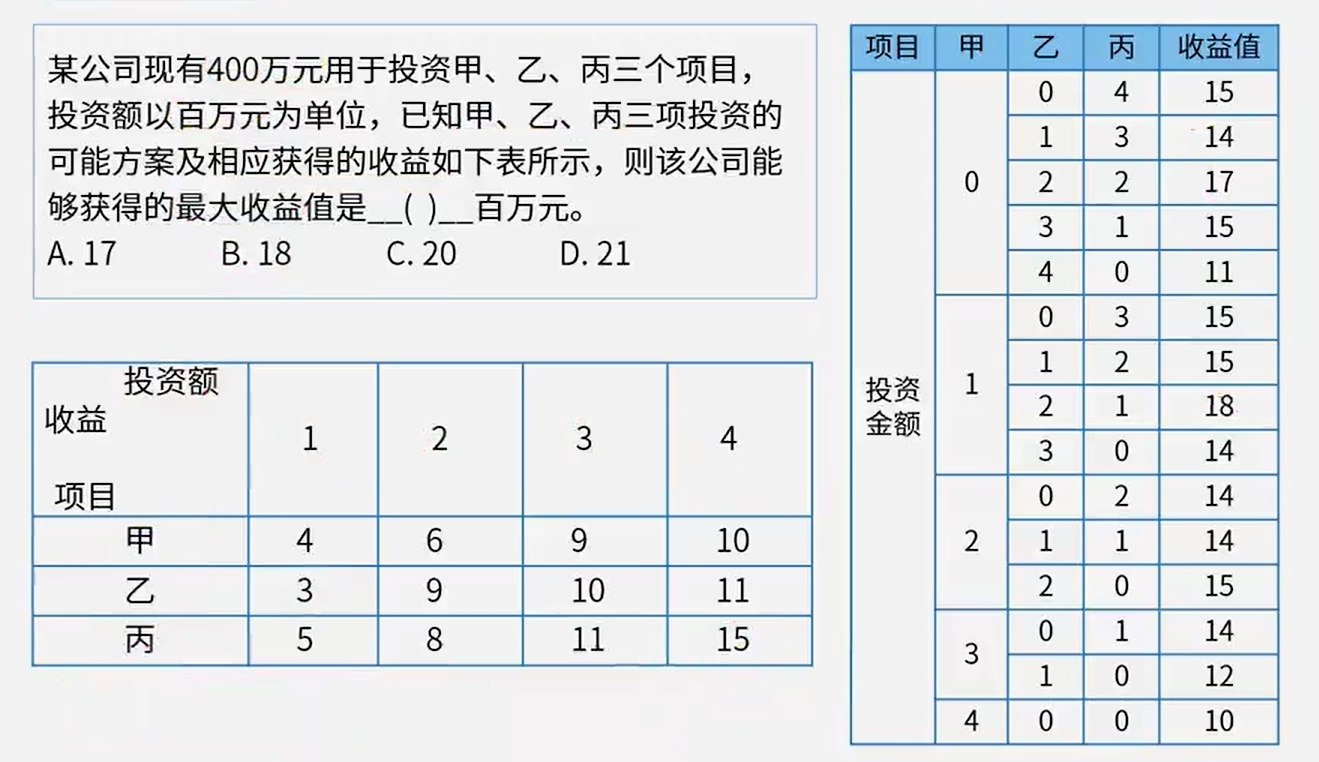
答案:B
骚戴理解:这个地方采用的就是暴力破解,把甲乙丙三种组合一个个列举出来,然后去计算总收益
讲解地址:78-动态规划_哔哩哔哩_bilibili
真题
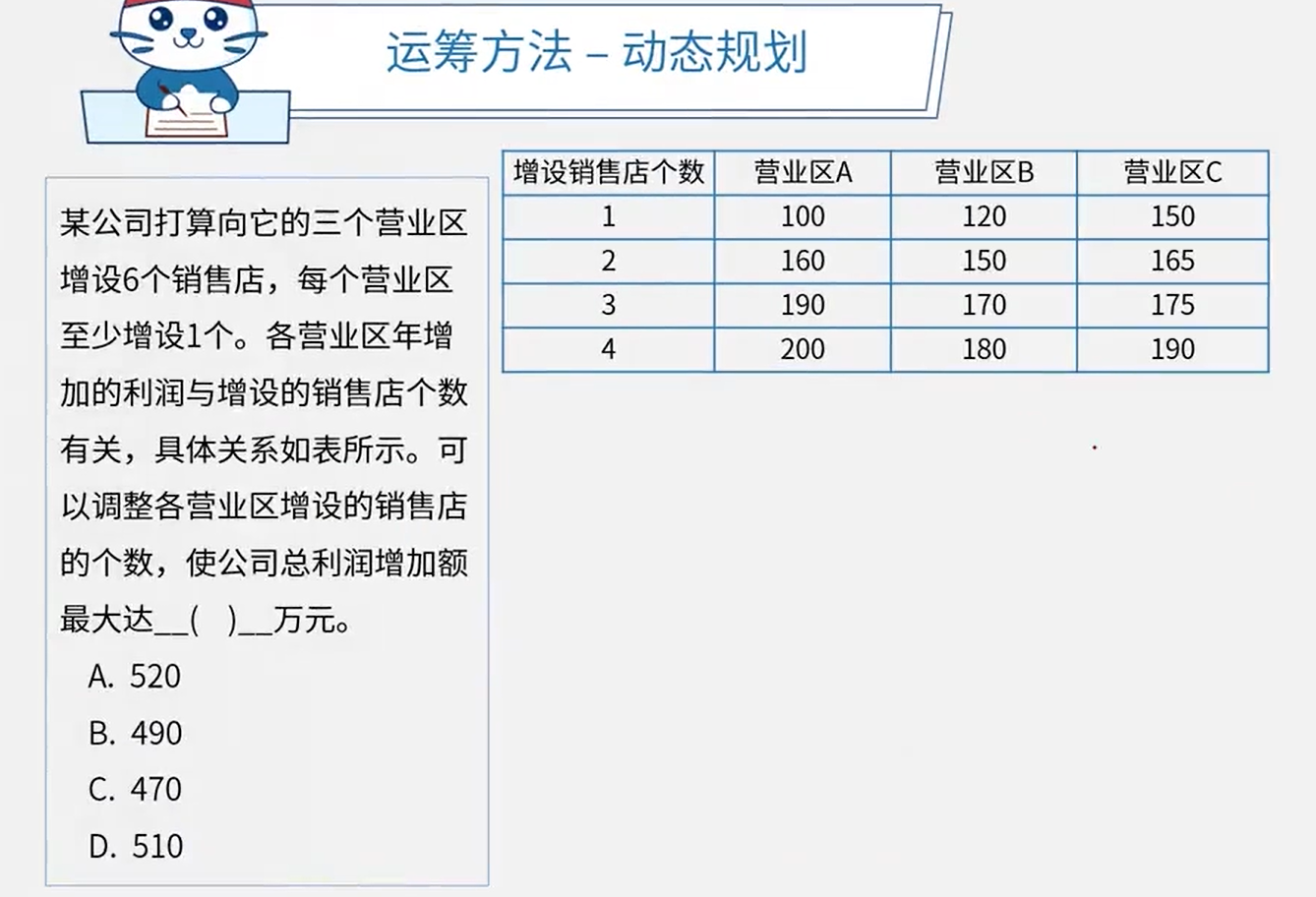
答案:B
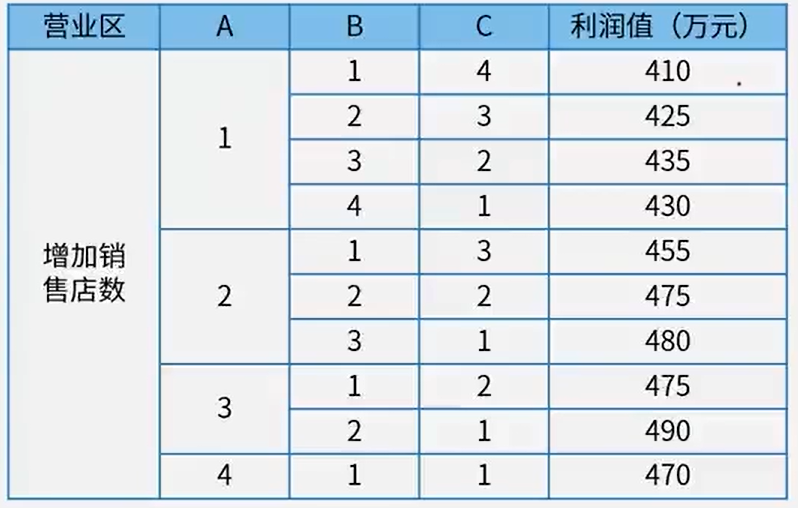
讲解地址:78-动态规划_哔哩哔哩_bilibili
真题
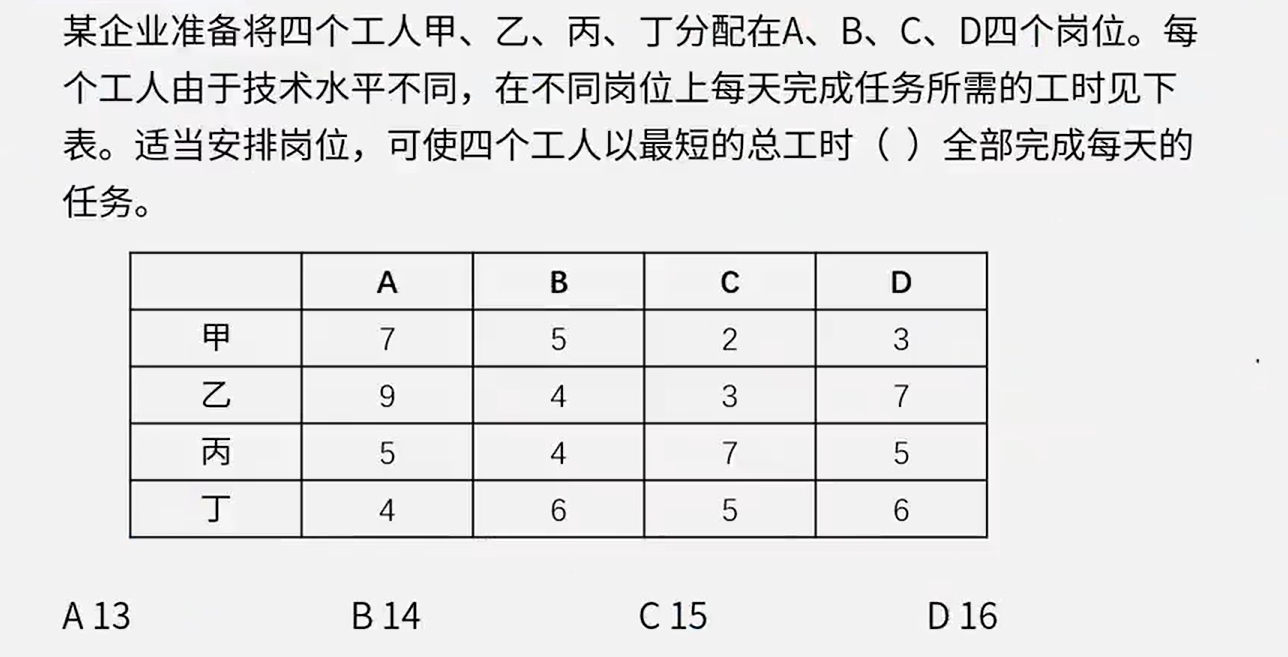
答案:B
讲解地址:78-动态规划_哔哩哔哩_bilibili
矩阵化简
真题


真题
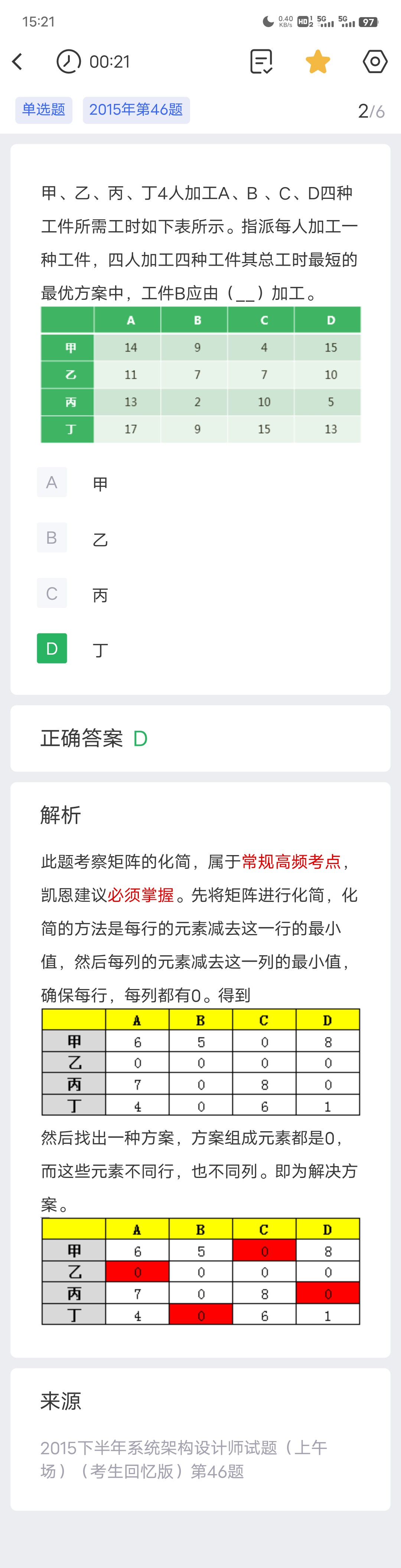
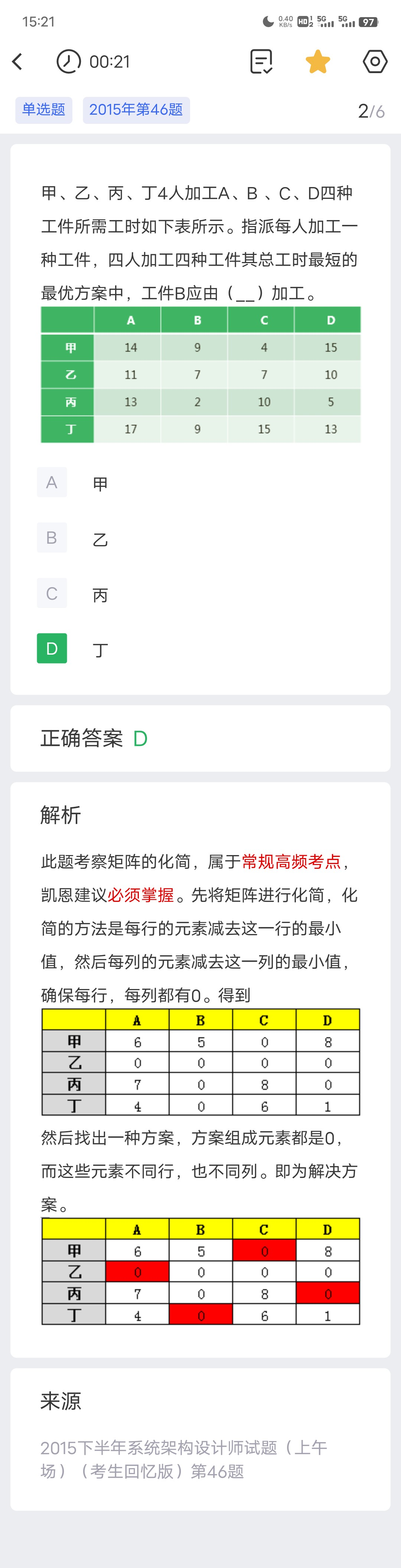
排队论

答案:C
讲解地址:79-排队论_哔哩哔哩_bilibili
博弈论
真题
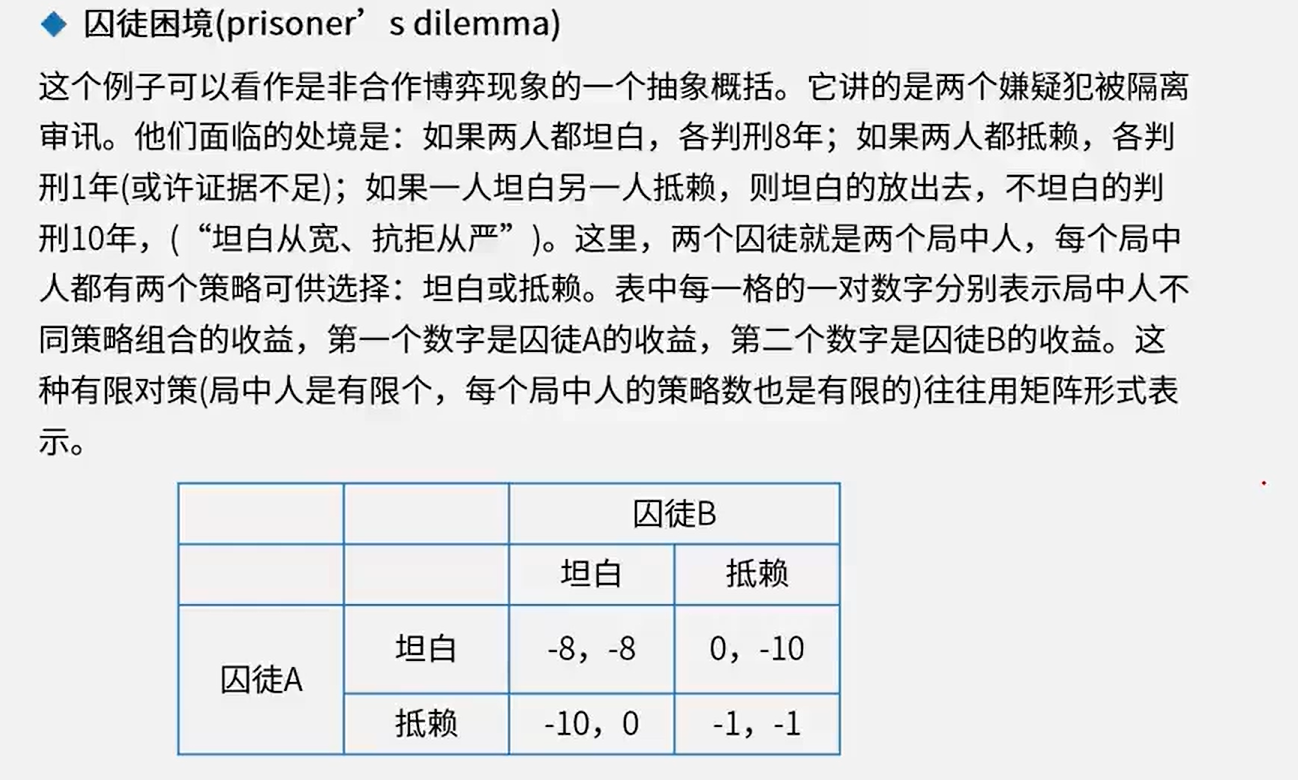
答案:囚犯A坦白,囚犯B抵赖
讲解地址:80-博弈论_哔哩哔哩_bilibili
真题

答案:甲选择低价,乙选择低价
骚戴理解:这里别搞混淆了,每一栏的两个数字分别代表甲的收益和乙的收益,首先捋清楚这一点,这样的题目很容易晕的
讲解地址:80-博弈论_哔哩哔哩_bilibili
状态转移矩阵
真题


真题


答案:C
骚戴理解:首先注意这个地方要算两次,因为是两个月以后,其次注意这里可以套用数学公式
讲解地址:81-状态转移矩阵_哔哩哔哩_bilibili
真题

答案:D
讲解地址:81-状态转移矩阵_哔哩哔哩_bilibili
不确定型决策

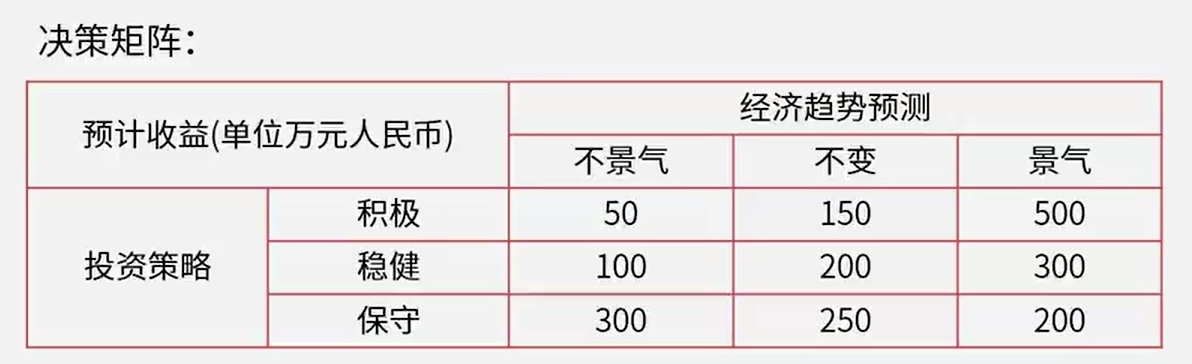
骚戴理解:
- 如果上面的决策矩阵采用乐观主义准则(大中取大),那就从每个策略的最大值中取最大值,也就是【500,300,300】,即取500,,所以选择积极策略
- 如果是悲观准则(小中取大),那就从每个策略的最小值中取最大值,也就是【50,100,200】中的最大值,即取200,所以选择保守策略
- 如果是等可能准则,那就要计算了,三种策略对应的计算公式如下所示,可以看到,其实最终也就是把这些值加起来看看谁最大就选谁,也就是【700,600,750】,所以选择保守策略
-
- 积极:(50+150+500)*(1/3)= 700 *(1/3)
- 稳健:(100+200+300)*(1/3) = 600 *(1/3)
- 保守:(300+250+200)*(1/3) = 750 *(1/3)
- 如果是后悔准则(最大后悔值选最小),那么需要还出下面的这个后悔值矩阵才行,然后在这个矩阵里面的最大后悔值中选最小值,然后从策略的角度来看,也就是【250,200,300】中取最小值,即取200,所以选择稳健策略,那这个后悔值怎么得出来的呢?这个后悔值其实就是一列列的看,然后取最大的值作为基础,计算其他的和这个基数的差值,差值就是后悔值,例如不景气这一列,最大值为300,那就是基数为300,然后其他的和基础的差值分别为250和200,那这些值就是对应的后悔值
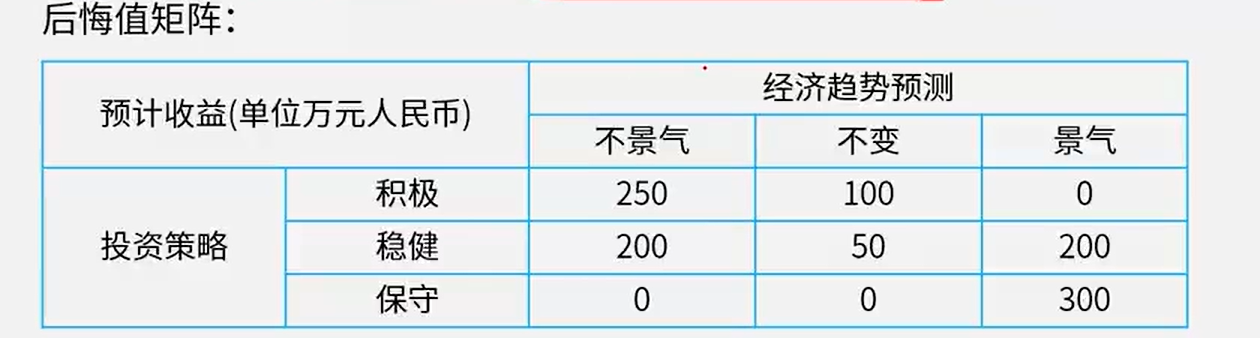
讲解地址:82-不确定型决策_哔哩哔哩_bilibili
决策表与决策树
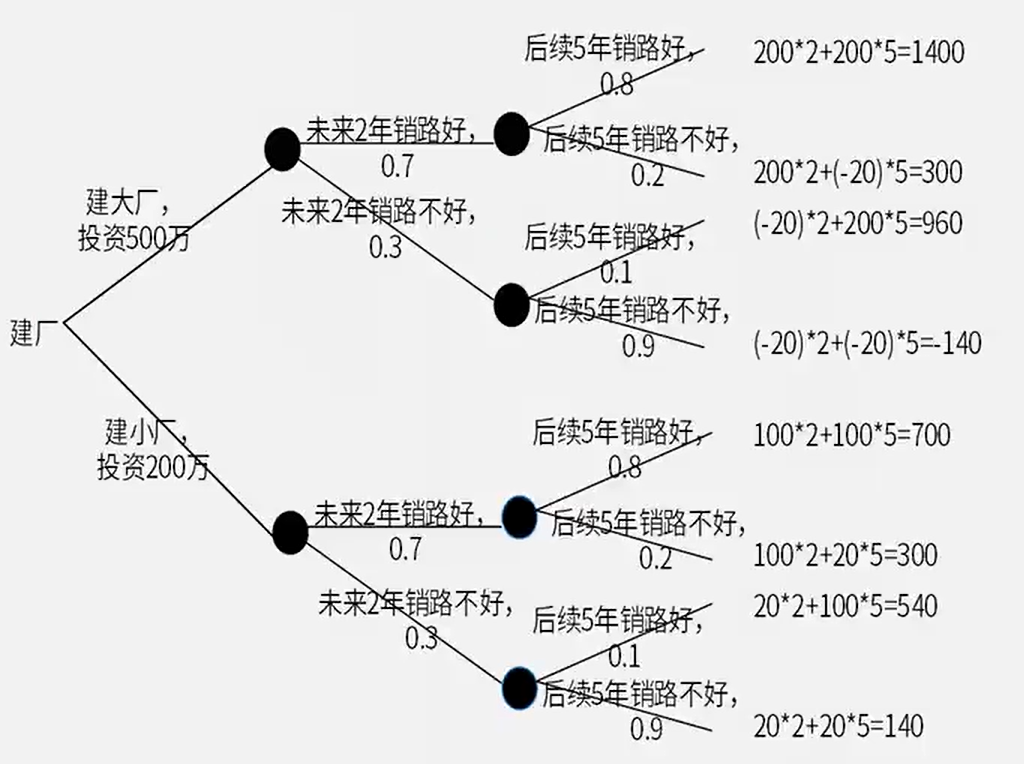
决策树
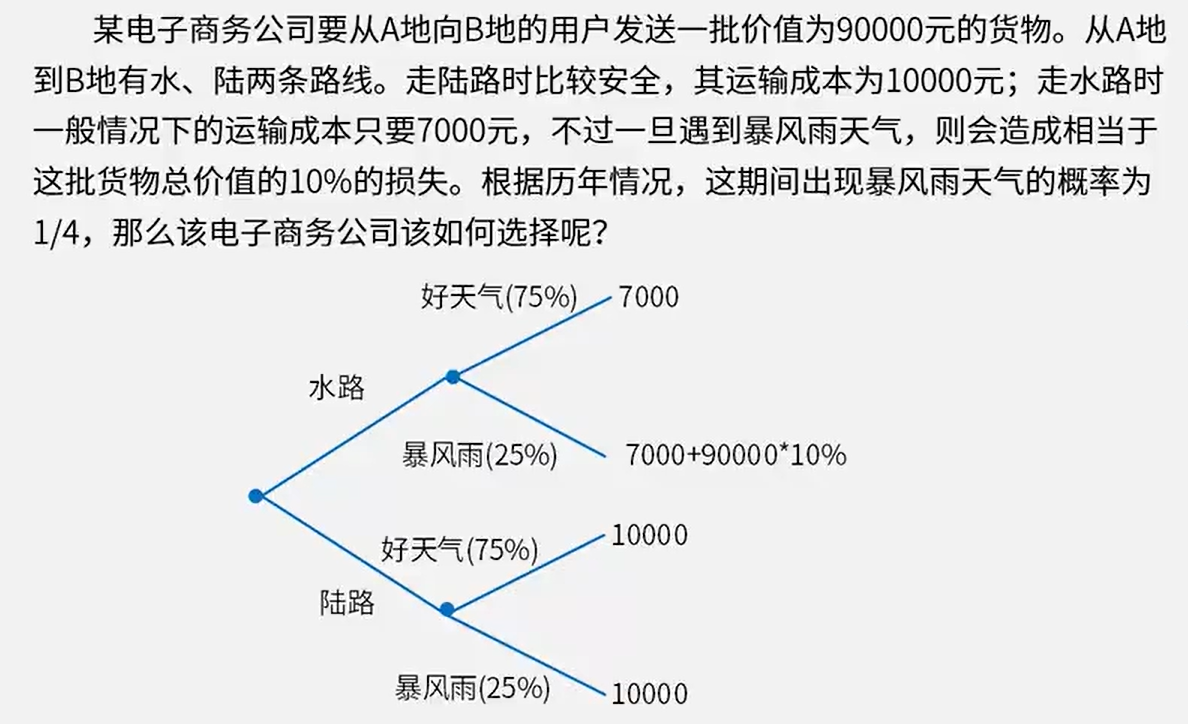
答案:水路
骚戴理解:这个题目首先会根据题目画出决策树,因为有的题目可能不给决策树,要自己画,其次就是要会求加权平均值,然后根据题目需求来决定是取最小值还是最大值,这里算的是成本,所以要取最小值,例如上面的这个题目的加权平均值如下所求
- 水路:7000*0.75+(7000+90000*10%)*0.25=9250
- 陆路:10000*0.75+10000*0.25 = 10000
决策表
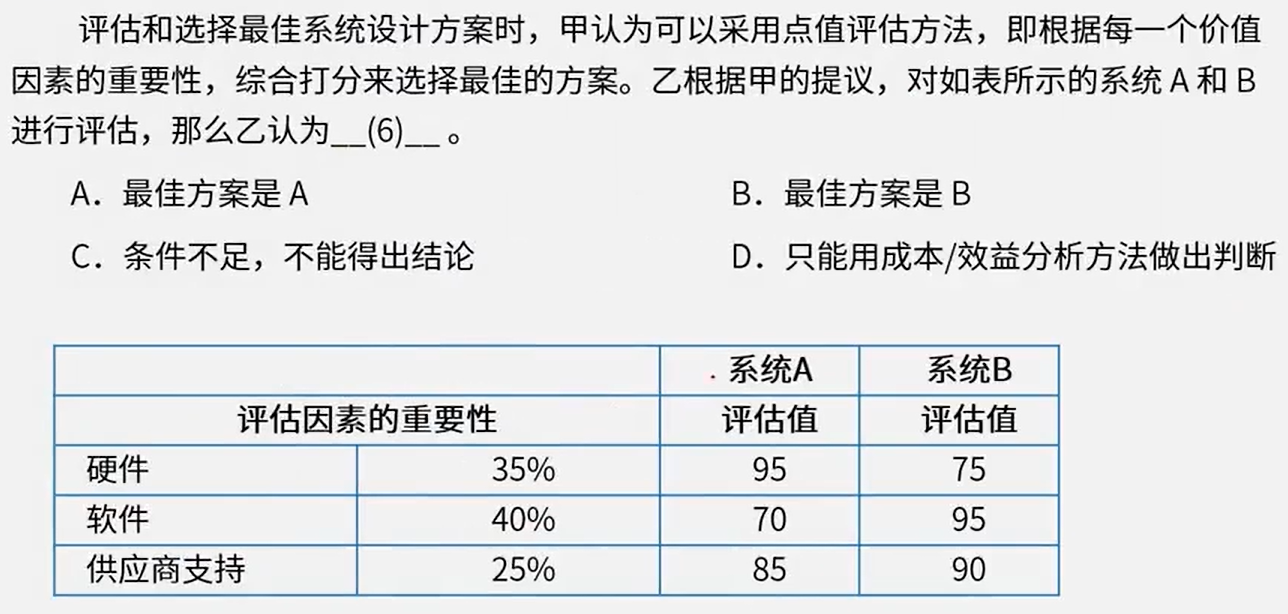
答案:B
骚戴理解:这个就跟简单了,也是求加权平均值,然后根据题目需求来决定是取最小值还是最大值,这里是求价值,那自然是取最大值
- A系统:95*35%+70*40%+85*25%=82.5
- B系统:75*35%+95*40%+90*25%=86.75
真题
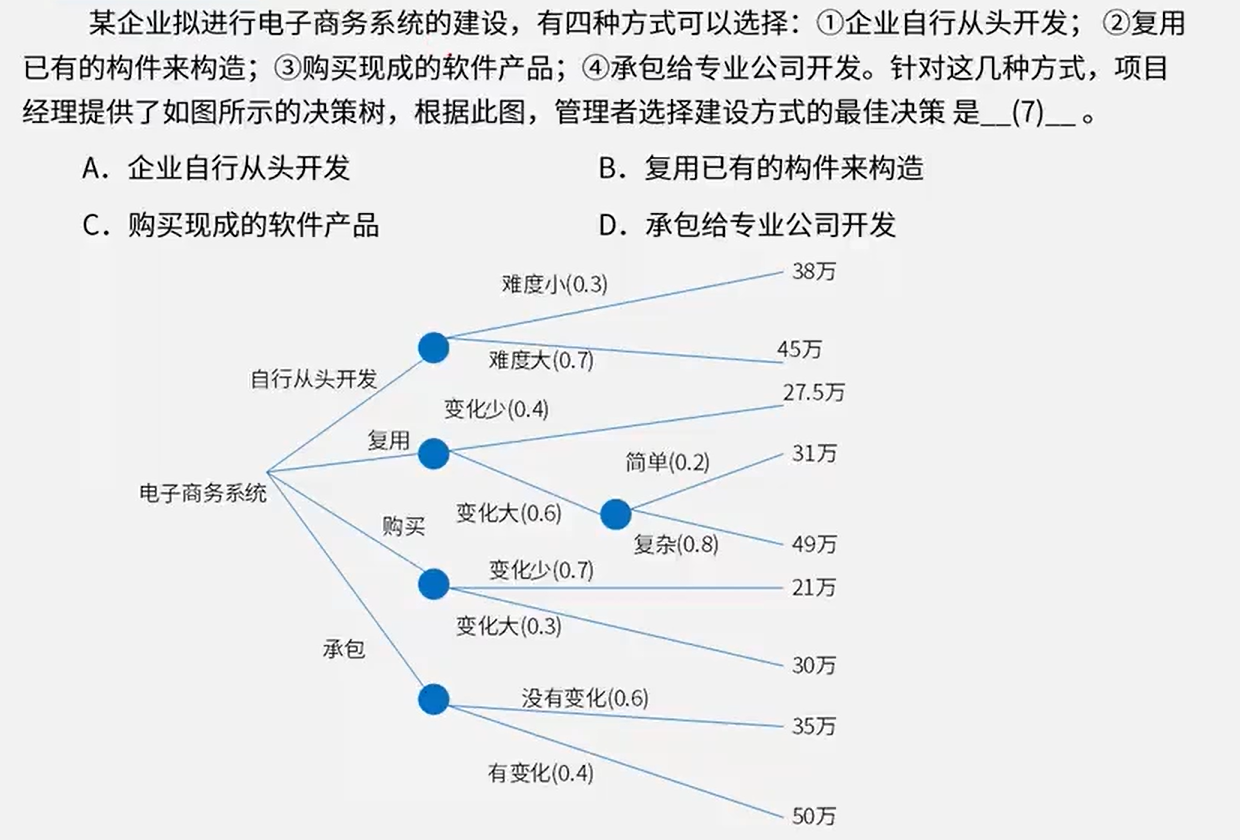
答案:C
骚戴理解:这个题目也一样是求加权平均值的,只是复用那里多了一个分支,这种情况用乘法即可,例如复用的情况计算加权平均值的公式:0.4*27.5+(0.6*0.2*31+0.6*0.8*49)=11+(3.72+23.52)=38.24
真题

答案:B
讲解地址:83-决策表与决策树_哔哩哔哩_bilibili
数学建模
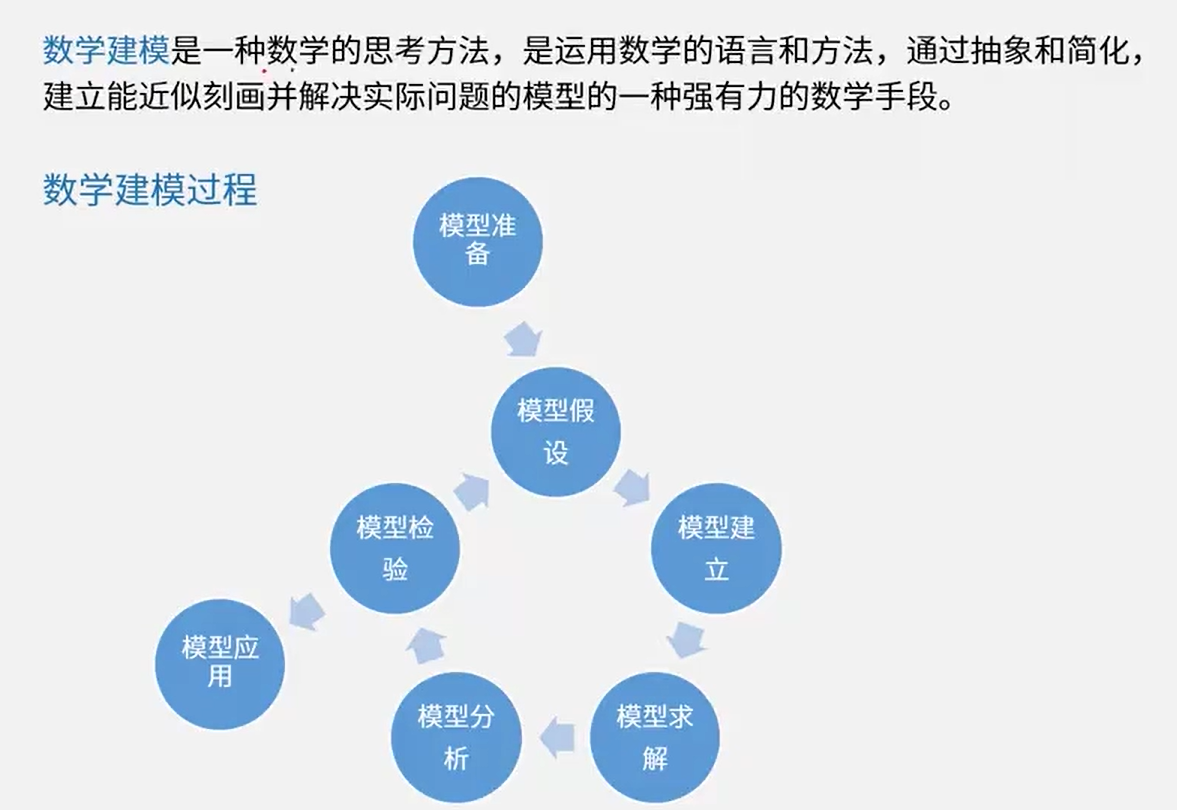
建模过程
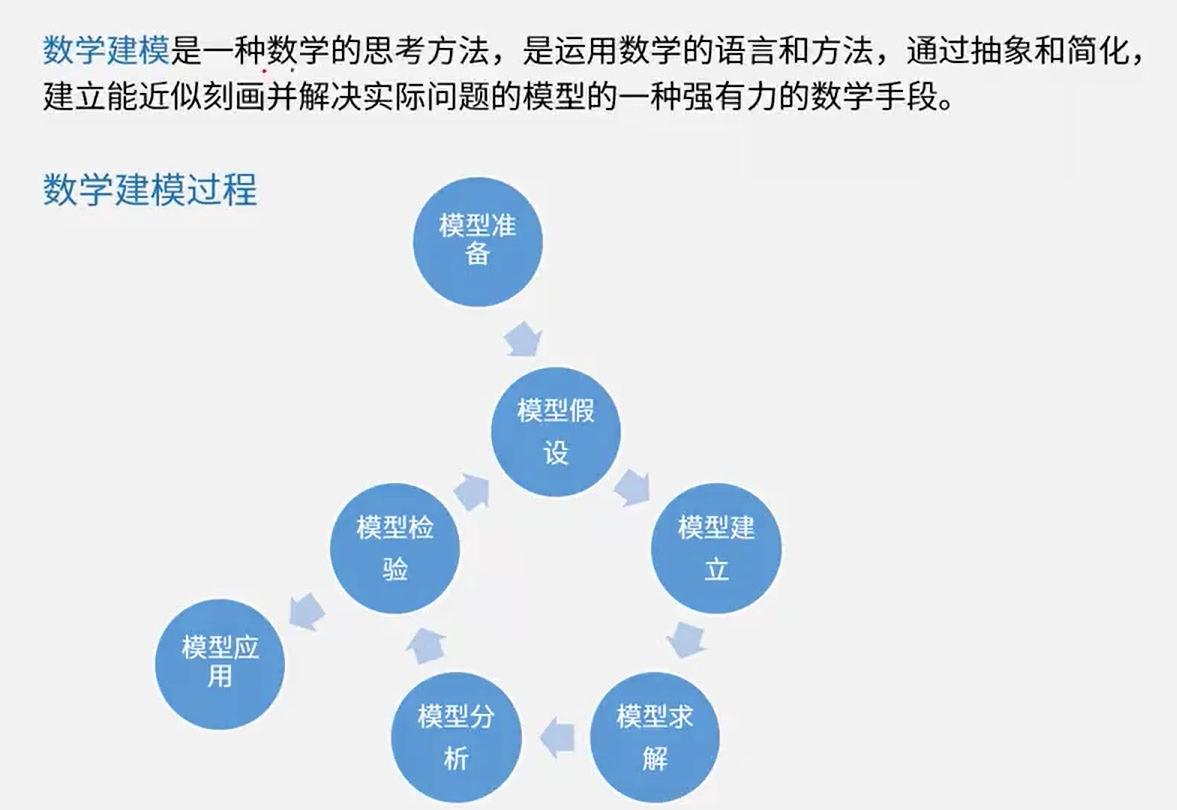

模型分析

模型校验

建模方法

真题


真题

答案:C
真题

答案:D
讲解地址:84-数学建模_哔哩哔哩_bilibili
无家可归
真题


真题
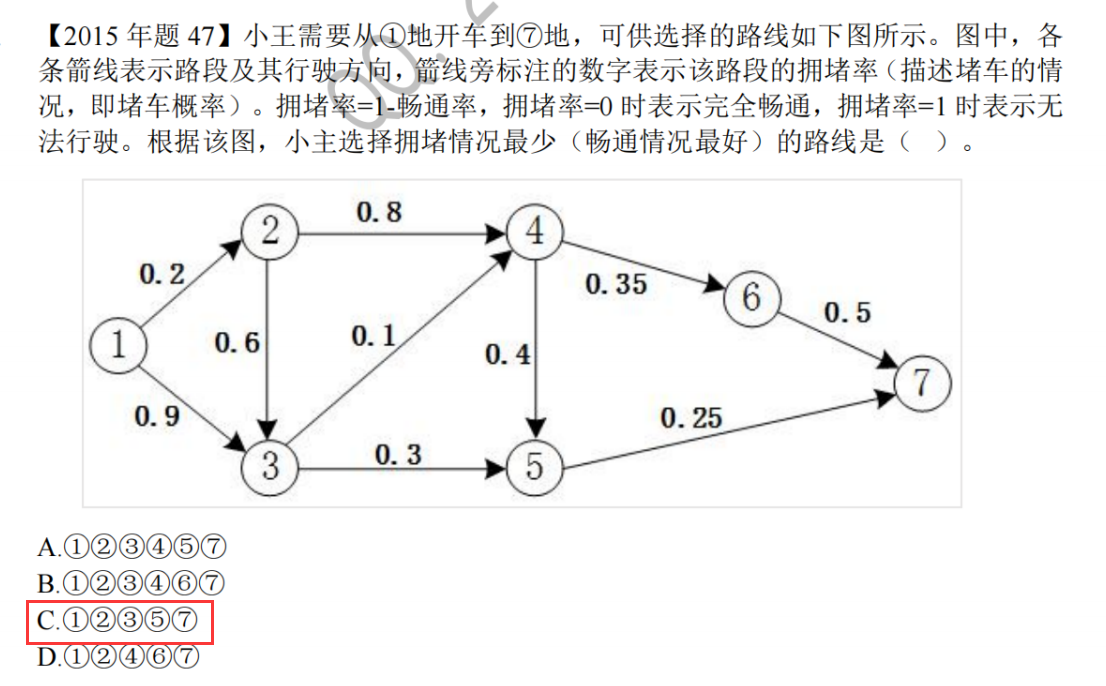

真题


真题
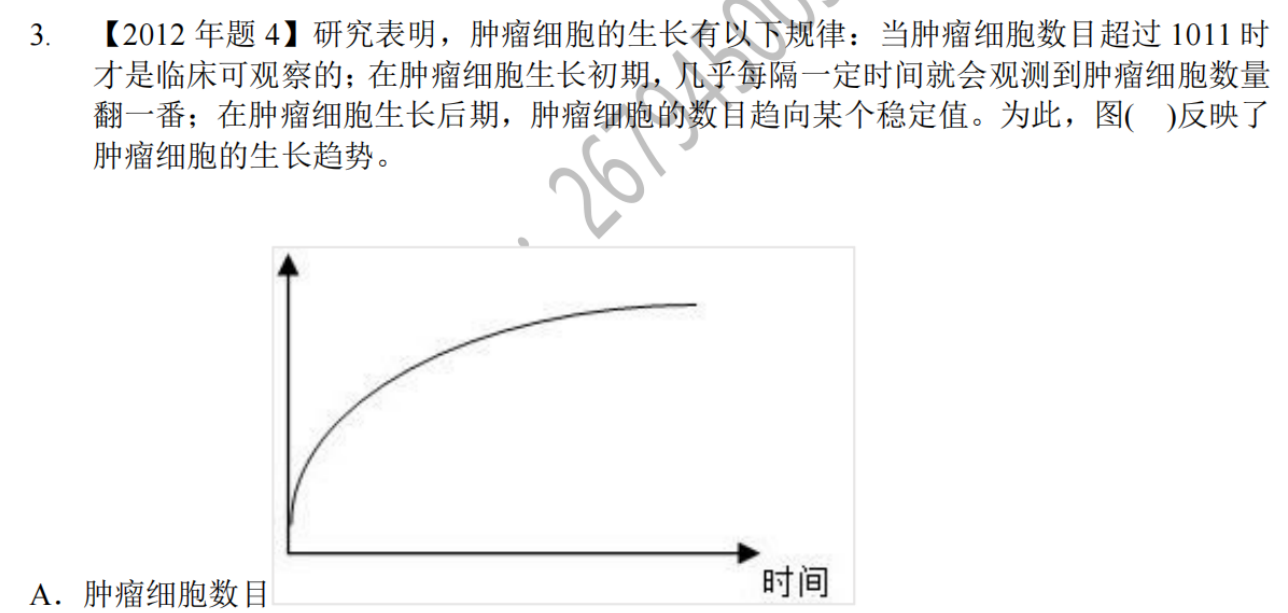

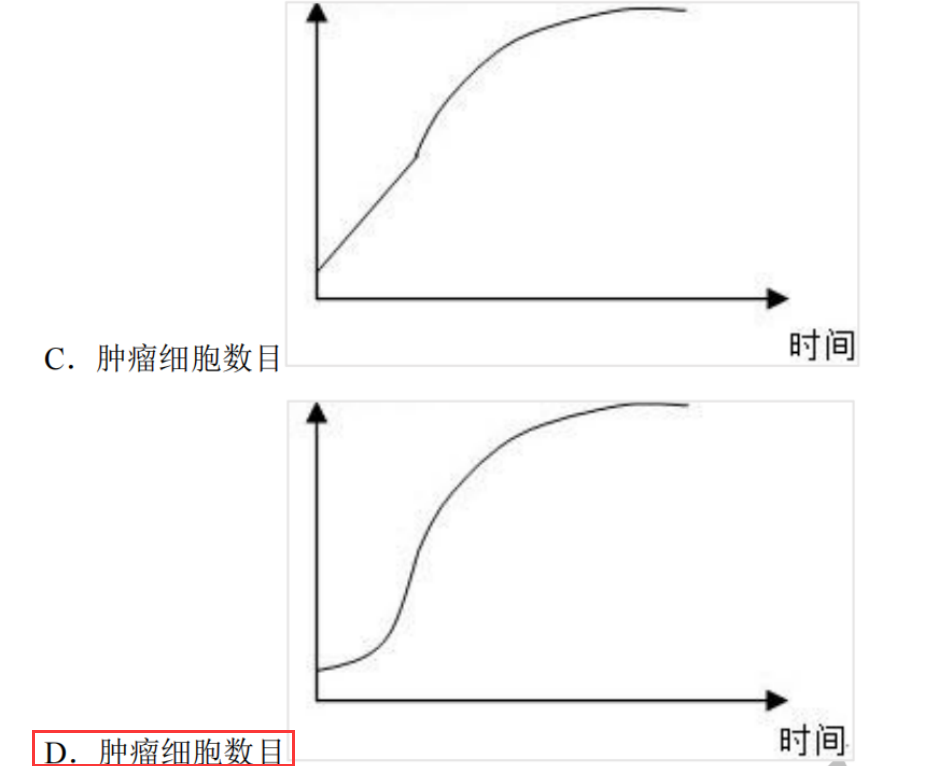


真题



真题

解析
此题考察蒙特卡洛算法的相关应用,属于常规高频考点。蒙特卡罗方法是一种统计模拟方法,其思想核心是通过模拟大量样本集或随机过程来近似实际问题对象。其名字来源于蒙特卡罗赌城,最初应用于20世纪40年代美国的曼哈顿原子弹计划,如今在数据分析和机器学习领域中有广泛的应用。蒙特卡罗方法的三个典型应用场景:近似计算不规则面积/体积/积分、模拟随机过程预测可能性结果区间范围、利用接受-拒绝采样进行对分布未知参数的统计推断
真题

真题
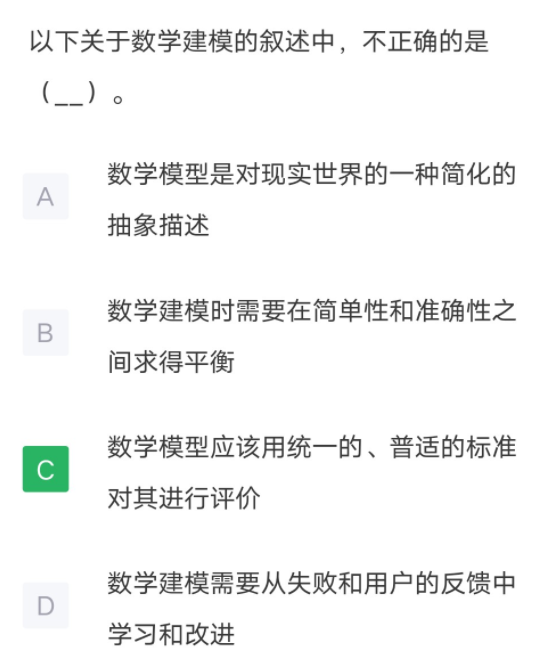
解析
此题考察数学建模的概念和特点,属于超纲低频考点。数学建模是利用数学方法解决实际问题的一种实践。数学建模的过程包括抽象、简化、假设、引入变量等步骤,建立数学模型,然后用先进的数学方法和计算机技术求解。数学模型是对于现实世界的一个特定对象、一个特定目的,根据特有的内在规律,作出一些必要的假设,运用适当的数学工具得到一个数学结构。对不同的问题,有不同的评价标准,数学模型难有统一的普适标准来评价。
真题



相关文章:

数学与经济管理
数学与经济管理(2-4分) 章节概述 最小生成树问题 答案:23 讲解地址:74-最小生成树问题_哔哩哔哩_bilibili 最短路径问题 答案:81 讲解地址:75-最短路径问题_哔哩哔哩_bilibili 网络与最大流量问题 真题 讲解…...

自动化测试系列 —— UI自动化测试
UI 测试是一种测试类型,也称为用户界面测试,通过该测试,我们检查应用程序的界面是否工作正常或是否存在任何妨碍用户行为且不符合书面规格的 BUG。了解用户将如何在用户和网站之间进行交互以执行 UI 测试至关重要,通过执行 UI 测试…...

眨个眼就学会了PixiJS
本文简介 带尬猴,我是德育处主任 当今的Web开发中,图形和动画已经成为了吸引用户注意力的重要手段之一。而 Pixi.js 作为一款高效、易用的2D渲染引擎,已经成为了许多开发者的首选(我吹的)。本文将为工友们介绍PixiJS的…...

WORD中的表格内容回车行距过大无法调整行距
word插入表格,编辑内容,换行遇到如下问题: 回车后行距过大,无法调整行距。 解决方法(并行): 方法1:选中要调整的内容,菜单路径:“编辑-清除-格式” 方法2&am…...

MySQL 高级函数整理
目录 MySQL 高级函数VERSIONIFCASE参考文章 MySQL 高级函数 函数描述BIN返回数字的二进制表示BINARY将值转换为二进制字符串CASE遍历条件并在满足第一个条件时返回一个值CAST将(任何类型的)值转换为指定的数据类型COALESCE返回列表中的第一个非空值CONN…...

UG\NX二次开发 连接曲线、连结曲线 UF_CURVE_auto_join_curves
文章作者:里海 来源网站:王牌飞行员_里海_里海NX二次开发3000例,里海BlockUI专栏,C\C++-CSDN博客 简介 UG\NX二次开发 连接曲线、连结曲线 UF_CURVE_auto_join_curves 效果 代码 #include "me.hpp" extern DllExport void ufusr(char* param, int* returnC…...
python爬虫入门(四)爬取猫眼电影排行(使用requests库和正则表达式)
本例中,利用 requests 库和正则表达式来抓取猫眼电影 TOP100 的相关内容。 1.目标 提取出猫眼电影 TOP100 的电影名称、时间、评分、图片等信息,提取的站点 URL 为 http://maoyan.com/board/4,提取的结果会以文件形式保存下来。 2.抓取分析…...

Mybatis-Plus CRUD
💗wei_shuo的个人主页 💫wei_shuo的学习社区 🌐Hello World ! Mybatis-Plus CRUD 通用 Service CRUD 封装 IService 接口,进一步封装 CRUD 采用 get 查询、remove 删除 、list 查询集合、page 分页的前缀命名方式区分 …...
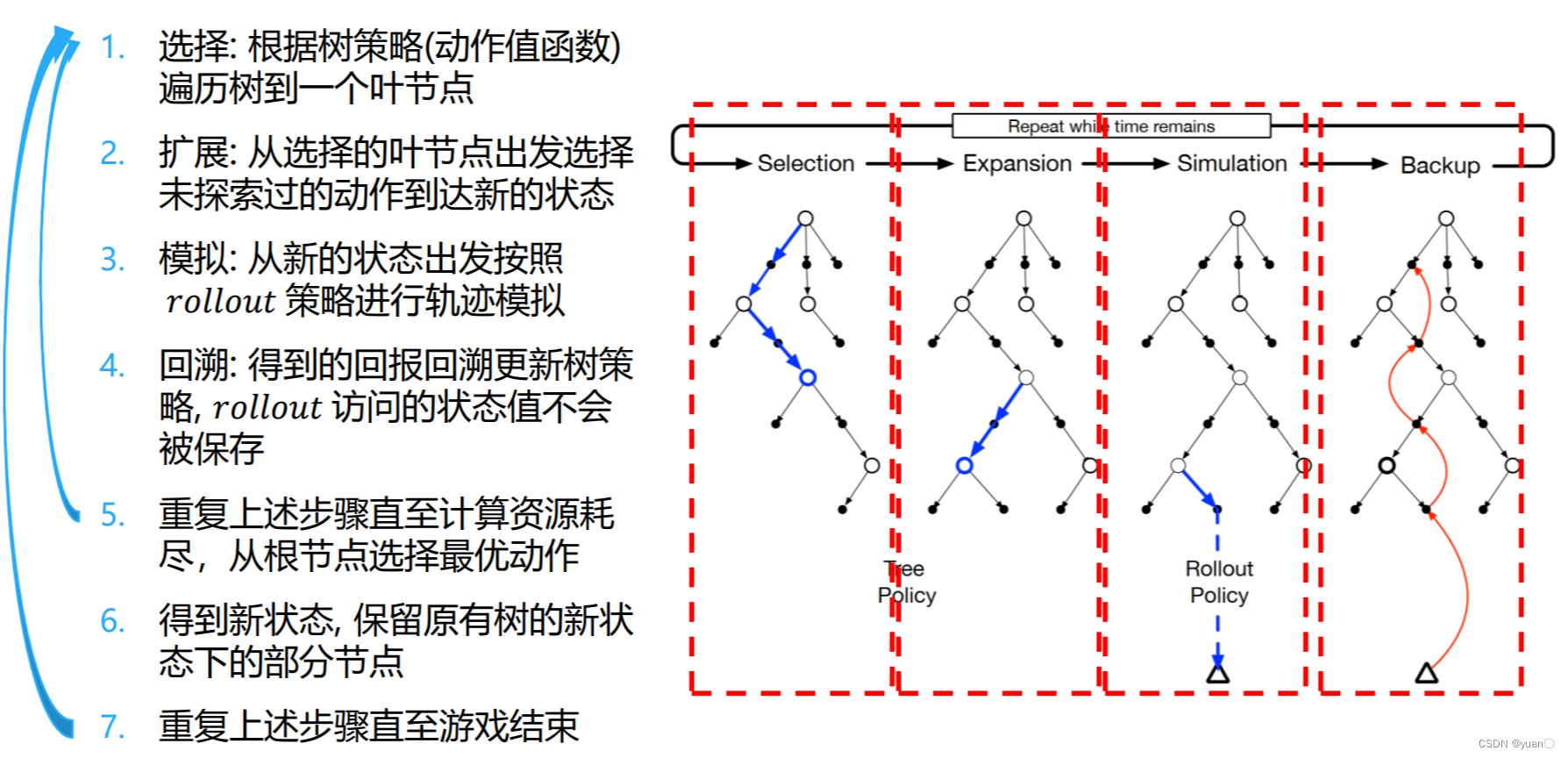
【强化学习】08——规划与学习(采样方法|决策时规划)
文章目录 优先级采样Example1 Prioritized Sweepingon Mazes局限性及改进 期望更新和采样更新不同分支因子下的表现 轨迹采样总结实时动态规划Example2 racetrack 决策时规划启发式搜索Rollout算法蒙特卡洛树搜索 参考 先做个简单的笔记整理,以后有时间再补上细节 …...
(链表) 25. K 个一组翻转链表 ——【Leetcode每日一题】
❓ 25. K 个一组翻转链表 难度:困难 给你链表的头节点 head ,每 k 个节点一组进行翻转,请你返回修改后的链表。 k 是一个正整数,它的值小于或等于链表的长度。如果节点总数不是 k 的整数倍,那么请将最后剩余的节点保…...
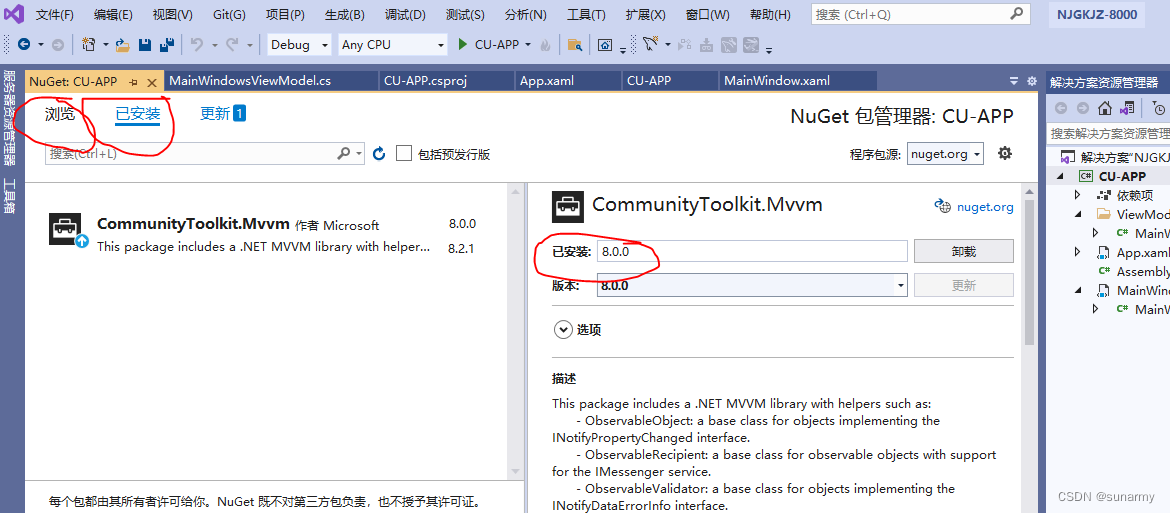
VisualStudio[WPF/.NET]基于CommunityToolkit.Mvvm架构开发
一、创建 "WPF应用程序" 新项目 项目模板选择如下: 暂时随机填一个目标框架,待会改: 二、修改“目标框架” 双击“解决方案资源管理器”中<项目>CU-APP, 打开<项目工程文件>CU-APP.csproj, 修改目标框架TargetFramew…...
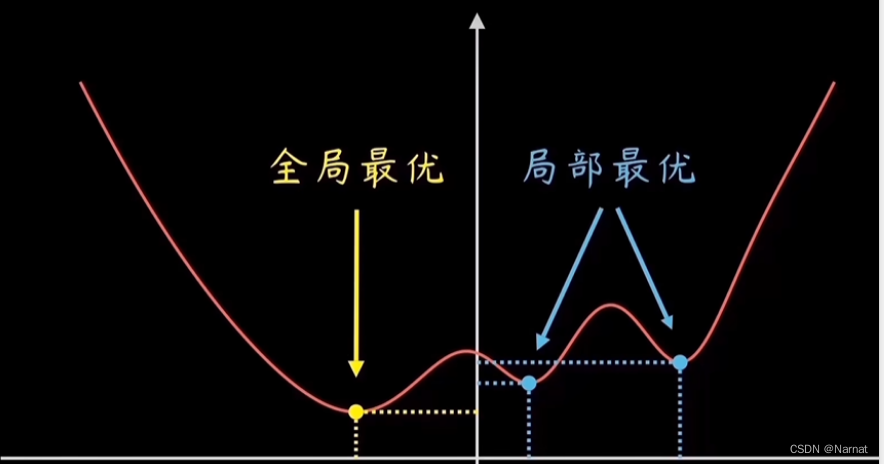
深度学习_5_模型拟合_梯度下降原理
需求: 想要找到一条直线,能更好的拟合这一些点 如何确定上述直线就是最优解呢? 由计算机算出所有点与我们拟合直线的误差,常见的是均方误差 例如:P1与直线之间的误差为e1 将P1坐标带入直线并求误差得: 推广到所有点&a…...

大模型时代,AI如何成为数实融合的驱动力?
10月25日,百度APP、百家号联合中兴通讯举办的“时代的增量“主题沙龙第二期在北京顺利召开。本期沙龙围绕“数实融合新视角”邀请学界、业界、媒体从业者等领域专家出席,以产学研相结合的视角深入探讨数实融合的最新技术趋势,并围绕数实融合在…...

MS COCO数据集的评价标准以及不同指标的选择推荐(AP、mAP、MS COCO、AR、@、0.5、0.75、1、目标检测、评价指标)
目标检测模型性能衡量指标、MS COCO 数据集的评价标准以及不同指标的选择推荐 0. 引言 0.1 COCO 数据集评价指标 目标检测模型通过 pycocotools 在验证集上会得到 COCO 的评价列表,具体参数的含义是什么呢? 0.2 目标检测领域常用的公开数据集 PASCAL …...

css实现鼠标多样化
cursor pointer: 手型default: 箭头text: 文本输入光标move: …...
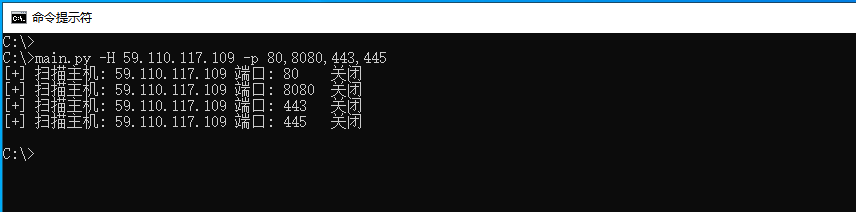
21.2 Python 使用Scapy实现端口探测
Scapy 是一款使用纯Python编写的跨平台网络数据包操控工具,它能够处理和嗅探各种网络数据包。能够很容易的创建,发送,捕获,分析和操作网络数据包,包括TCP,UDP,ICMP等协议,此外它还提…...
Qt设计一个自定义的登录框窗口
今天写了一个Qt登录、注册的小demo,后续完善会连接MySQL使用,过几天写完我会放在github上。 主要页面: 动态演示: 写完这个界面后,我终于知道了Qt为什么几乎没什么好看的窗口设计了,随便写一个简单大方的登…...
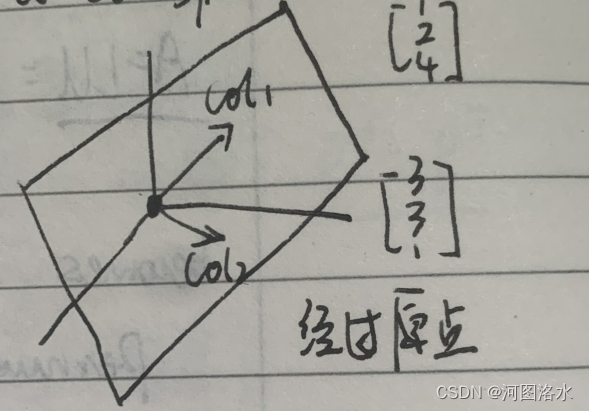
05 MIT线性代数-转置,置换,向量空间Transposes, permutations, spaces
1. Permutations P: execute row exchanges becomes PA LU for any invertible A Permutations P identity matrix with reordered rows mn (n-1) ... (3) (2) (1) counts recordings, counts all nxn permuations 对于nxn矩阵存在着n!个置换矩阵 , 2. Transpose: 2.…...
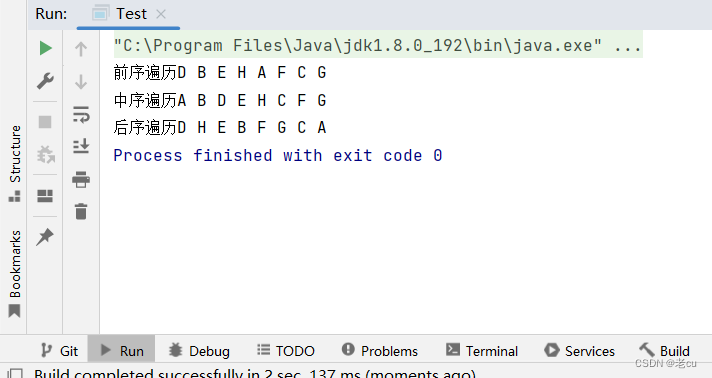
[数据结构】二叉树
1.概念 一棵二叉树是结点的一个有限集合,该集合: 1. 或者为空 2. 或者是由一个根节点加上两棵别称为左子树和右子树的二叉树组成 从上图我们可以发现: 1.二叉树不存在大于2 的度 2.二叉树的子树有左右之分,次序不能颠倒。是有…...
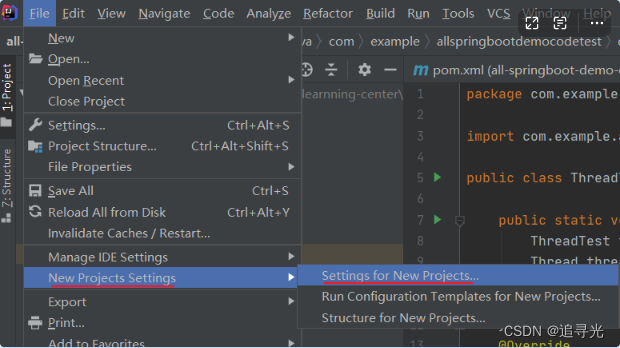
idea 中配置 maven
前文叙述: 配置 maven 一共要设置两个地方:1、为当前项目设置2、为新项目设置maven 的下载和安装可参考我之前写过的文章,具体的配置文章中也都有讲解。1、为当前项目进行 maven 配置 配置 VM Options: -DarchetypeCataloginternal2、为新项…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

数学建模-滑翔伞伞翼面积的设计,运动状态计算和优化 !
我们考虑滑翔伞的伞翼面积设计问题以及运动状态描述。滑翔伞的性能主要取决于伞翼面积、气动特性以及飞行员的重量。我们的目标是建立数学模型来描述滑翔伞的运动状态,并优化伞翼面积的设计。 一、问题分析 滑翔伞在飞行过程中受到重力、升力和阻力的作用。升力和阻力与伞翼面…...

ZYNQ学习记录FPGA(一)ZYNQ简介
一、知识准备 1.一些术语,缩写和概念: 1)ZYNQ全称:ZYNQ7000 All Pgrammable SoC 2)SoC:system on chips(片上系统),对比集成电路的SoB(system on board) 3)ARM:处理器…...
