图论基础和表示
一、概念及其介绍
图论(Graph Theory)是离散数学的一个分支,是一门研究图(Graph)的学问。
图是用来对对象之间的成对关系建模的数学结构,由"节点"或"顶点"(Vertex)以及连接这些顶点的"边"(Edge)组成。
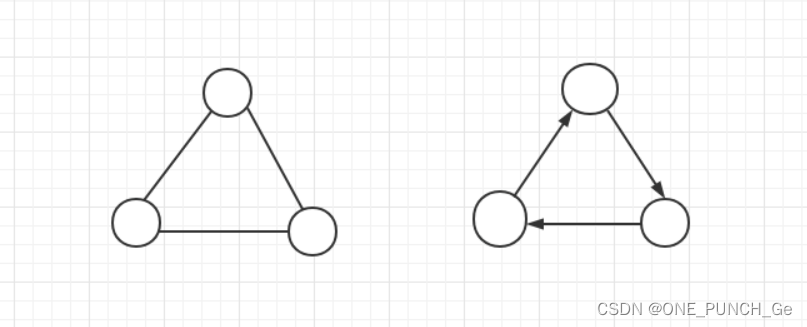
值得注意的是,图的顶点集合不能为空,但边的集合可以为空。图可能是无向的,这意味着图中的边在连接顶点时无需区分方向。否则,称图是有向的。下面左图是一个典型的无向图结构,右图则属于有向图。本章节介绍的图都是无向图。
图的分类:无权图和有权图,连接节点与节点的边是否有数值与之对应,有的话就是有权图,否则就是无权图。
图的连通性:在图论中,连通图基于连通的概念。在一个无向图 G 中,若从顶点 i 到顶点 j 有路径相连(当然从j到i也一定有路径),则称 i 和 j 是连通的。如果 G 是有向图,那么连接i和j的路径中所有的边都必须同向。如果图中任意两点都是连通的,那么图被称作连通图。如果此图是有向图,则称为强连通图(注意:需要双向都有路径)。图的连通性是图的基本性质。
完全图:完全是一个简单的无向图,其中每对不同的顶点之间都恰连有一条边相连。
自环边:一条边的起点终点是一个点。
平行边:两个顶点之间存在多条边相连接。
二、适用说明
图可用于在物理、生物、社会和信息系统中建模许多类型的关系和过程,许多实际问题可以用图来表示。因此,图论成为运筹学、控制论、信息论、网络理论、博弈论、物理学、化学、生物学、社会科学、语言学、计算机科学等众多学科强有力的数学工具。在强调其应用于现实世界的系统时,网络有时被定义为一个图,其中属性(例如名称)之间的关系以节点和或边的形式关联起来。
三、图的表达形式
邻接矩阵:1 表示相连接,0 表示不相连。
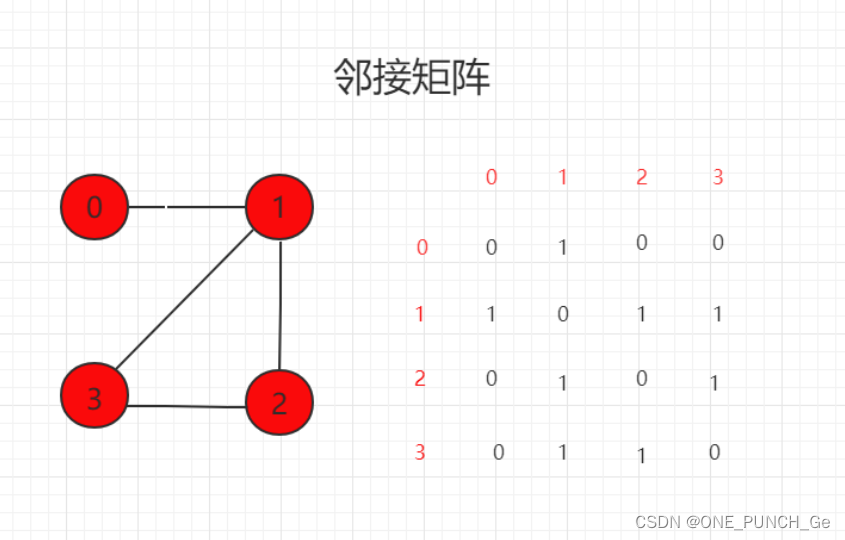
邻接表:只表达和顶点相连接的顶点信息
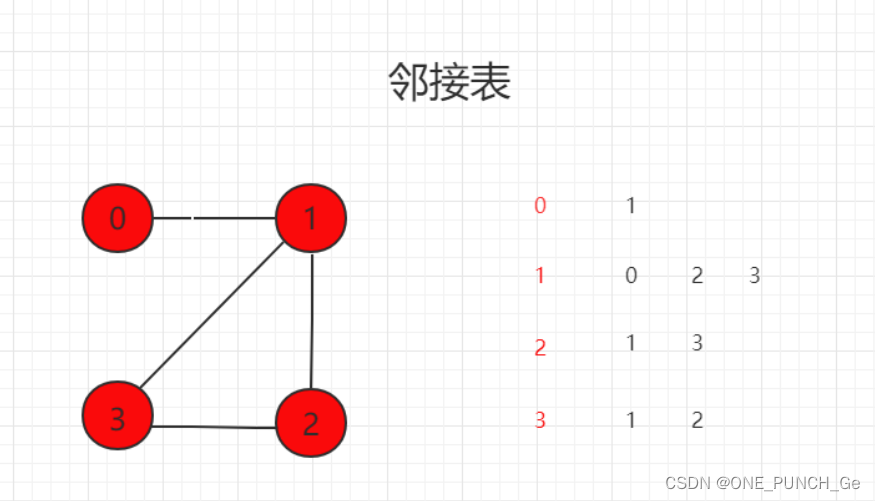
邻接表适合表示稀疏图 (Sparse Graph)
邻接矩阵适合表示稠密图 (Dense Graph)
Java 实例代码
(1) 邻接矩阵
src/runoob/graph/DenseGraph.java 文件代码:
package runoob.graph;/*** 邻接矩阵*/
public class DenseGraph {// 节点数private int n;// 边数private int m;// 是否为有向图private boolean directed;// 图的具体数据private boolean[][] g;// 构造函数public DenseGraph( int n , boolean directed ){assert n >= 0;this.n = n;this.m = 0;this.directed = directed;// g初始化为n*n的布尔矩阵, 每一个g[i][j]均为false, 表示没有任和边// false为boolean型变量的默认值g = new boolean[n][n];}// 返回节点个数public int V(){ return n;}// 返回边的个数public int E(){ return m;}// 向图中添加一个边public void addEdge( int v , int w ){assert v >= 0 && v < n ;assert w >= 0 && w < n ;if( hasEdge( v , w ) )return;g[v][w] = true;if( !directed )g[w][v] = true;m ++;}// 验证图中是否有从v到w的边boolean hasEdge( int v , int w ){assert v >= 0 && v < n ;assert w >= 0 && w < n ;return g[v][w];}
}(2)邻接表
src/runoob/graph/SparseGraph.java 文件代码:
package runoob.graph;import java.util.Vector;/*** 邻接表*/
public class SparseGraph {// 节点数private int n;// 边数private int m;// 是否为有向图private boolean directed;// 图的具体数据private Vector<Integer>[] g;// 构造函数public SparseGraph( int n , boolean directed ){assert n >= 0;this.n = n;this.m = 0; this.directed = directed;// g初始化为n个空的vector, 表示每一个g[i]都为空, 即没有任和边g = (Vector<Integer>[])new Vector[n];for(int i = 0 ; i < n ; i ++)g[i] = new Vector<Integer>();}// 返回节点个数public int V(){ return n;}// 返回边的个数public int E(){ return m;}// 向图中添加一个边public void addEdge( int v, int w ){assert v >= 0 && v < n ;assert w >= 0 && w < n ;g[v].add(w);if( v != w && !directed )g[w].add(v);m ++;}// 验证图中是否有从v到w的边boolean hasEdge( int v , int w ){assert v >= 0 && v < n ;assert w >= 0 && w < n ;for( int i = 0 ; i < g[v].size() ; i ++ )if( g[v].elementAt(i) == w )return true;return false;}
}相关文章:

图论基础和表示
一、概念及其介绍 图论(Graph Theory)是离散数学的一个分支,是一门研究图(Graph)的学问。 图是用来对对象之间的成对关系建模的数学结构,由"节点"或"顶点"(Vertex)以及连接这些顶点的"边"(Edge&a…...

STM32 音频ADC转wav格式
STM32 音频ADC DAC测试方法_stm32 adc 音频-CSDN博客 STM32--vs1053 WAV录音实现(保存在SD卡)_vs1053 多字节读取-CSDN博客 单片机内部AD实现录音wav文件_adc语音信号采样_天外飞仙CUG的博客-CSDN博客 PCM编码格式_pcm格式-CSDN博客 用ADC编码PCM数据…...

面试中经常问道的问题二
深入理解前端跨域方法和原理 前言 受浏览器同源策略的限制,本域的js不能操作其他域的页面对象(比如DOM)。但在安全限制的同时也给注入iframe或是ajax应用上带来了不少麻烦。所以我们要通过一些方法使本域的js能够操作其他域的页面对象或者使…...

SQL UPDATE 语句(更新表中的记录)
SQL UPDATE 语句 UPDATE 语句用于更新表中已存在的记录。 还可以使用AND或OR运算符组合多个条件。 SQL UPDATE 语法 具有WHERE子句的UPDATE查询的基本语法如下所示: UPDATE table_name SET column1 value1, column2 value2, ... WHERE conditi…...

js节流和防抖
节流(throttle)和防抖(debounce)是为了解决函数频繁触发而引发性能问题的两种优化方法。 节流: 指定一个时间间隔,在时间间隔内只执行一次函数,即在一段时间内,多次触发函数只执行一…...
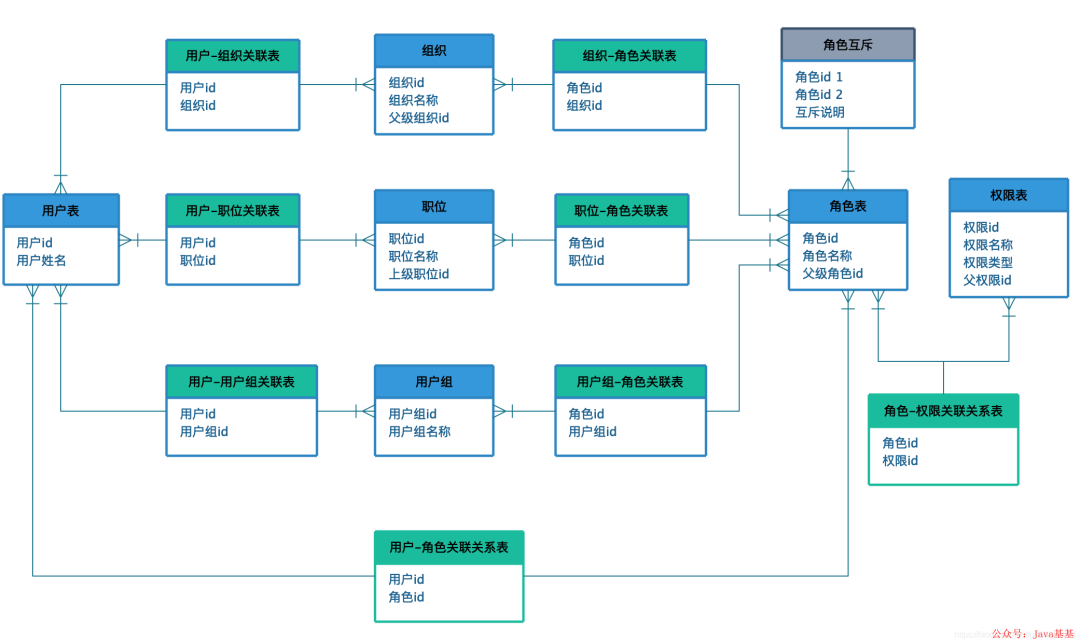
权限系统设计(转载)
1 为什么需要权限管理 2 权限模型 2.1 权限设计 2.2 为什么需要角色 2.3 权限模型的演进 2.4 用户划分 2.5 理想的RBAC模型 3 权限系统表设计 3.1 标准RBAC模型表设计 3.2 理想RBAC模型表设计 4 结语 1 为什么需要权限管理 日常工作中权限的问题时时刻刻伴随着我们&a…...
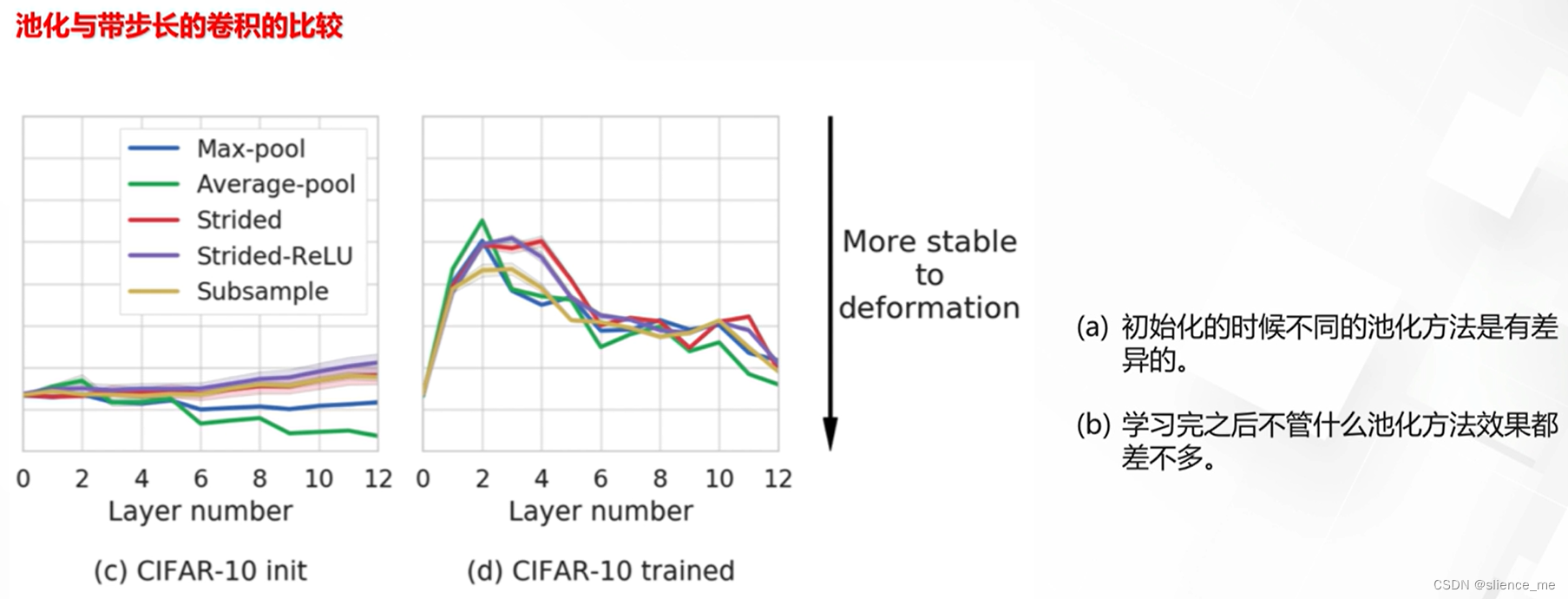
【机器学习合集】标准化与池化合集 ->(个人学习记录笔记)
文章目录 标准化与池化1. 标准化/归一化1.1 归一化归一化的作用 1.2 标准化批标准化方法 Batch Normailzation标准化方法的对比自动学习标准化方法 2. 池化2.1 池化的作用2.2 常见的池化方法2.3 池化方法的差异2.4 池化的必要性 标准化与池化 1. 标准化/归一化 1.1 归一化 归…...

Dockerfile文件自动化生成R4L镜像
Dockerfile文件自动化生成R4L镜像的步骤 1、安装Docker:2、使用Dockerfile一键生成镜像:3、查看生成的Docker镜像:4、删除Docker镜像:5、生成Docker容器:6、查看容器7、删除容器 1、安装Docker: curl -fsS…...
基于SSM的居家养老系统
末尾获取源码 开发语言:Java Java开发工具:JDK1.8 后端框架:SSM 前端:Vue 数据库:MySQL5.7和Navicat管理工具结合 服务器:Tomcat8.5 开发软件:IDEA / Eclipse 是否Maven项目:是 目录…...

[C#基础训练]FoodRobot食品管理部分代码-2
参考代码: using System; using System.Collections.Generic;namespace FoodRobotDemo {public class FoodInfo{ public string Name { get; set; } public int Id { get; set; } public int Count { get; set; }}public class FoodRobot{private …...
docker部署rabbitmq的坑
背景 今天用docker部署rabbitmq,启动都一起正常,但是当访问15672端口时,不能加载出页面。 排查 1.防火墙是否开启 ufw status2.ip是否能ping通 ping 192.168.x.x3.检查docker日志 docker psdocker logs -f 容器id4.进入容器,…...
】 python和vba读写EXCEL文件的方式比较 (建设ing))
【python VS vba(系列2)】 python和vba读写EXCEL文件的方式比较 (建设ing)
目录 1 用VBA读写EXCEL文件 1.1 用VBA读写,本工作簿workbook里的特定sheet的特定内容 1.1.1 EXCEL表内内容访问 1.1.2 注意点 1.1.3 代码 1.2 用VBA读写本工作簿workbook里的所有sheet的内容 1.2.1 麻烦之处 1.2.2 方法,如何指定EXCEL里的内容…...

小程序 swiper滑动 层叠滑动效果
整个红色区域为可滑动区域,数字1区域为展示区域,数字2为下一个展示模块 <scroll-view class"h_scroll_horizontal" enhanced"ture" bind:touchend"touchEnd" bind:touchstart"touchStart"><view clas…...

【20年VIO梳理】
19-20年VIO 梳理 1. 开源代码介绍: DSM2. FMD Stereo SLAM:融合MVG和直接方法,实现准确,快速的双目SLAM3. 基于VINS-Mono开发的SPVIS4. 改进:一种基于光流的动态环境移动机器人定位方案5. PVIO:基于先验平面约束的高效…...

Java Object类详解
Object 是 java 类库中的一个特殊类,也是所有类的父类。也就是说,Java 允许把任何类型的对象赋给 Object 类型的变量。当一个类被定义后,如果没有指定继承的父类,那么默认父类就是 Object 类。因此,以下两个类表示的含…...
Unity 中忽略图片透明度的 Image 组件的修改版本
只需将此组件添加到画布中的空对象即可。请注意,仅支持简单 图像类型。 using System.Collections.Generic; using UnityEngine; using UnityEngine.Sprites; using UnityEngine.UI; #if UNITY_2017_4 || UNITY_2018_2_OR_NEWER using UnityEngine.U2D; #endif#if U…...
hibernate源码(1)--- schema创建
sessionFactory 配置项: hibernate的核心是sessionFactory,那我们看看如何构建session Factory。 参考官网: plugins {id("java") } group "com.atai.hibernatespy" version "1.0-SNAPSHOT" repositories…...

数学与经济管理
数学与经济管理(2-4分) 章节概述 最小生成树问题 答案:23 讲解地址:74-最小生成树问题_哔哩哔哩_bilibili 最短路径问题 答案:81 讲解地址:75-最短路径问题_哔哩哔哩_bilibili 网络与最大流量问题 真题 讲解…...

自动化测试系列 —— UI自动化测试
UI 测试是一种测试类型,也称为用户界面测试,通过该测试,我们检查应用程序的界面是否工作正常或是否存在任何妨碍用户行为且不符合书面规格的 BUG。了解用户将如何在用户和网站之间进行交互以执行 UI 测试至关重要,通过执行 UI 测试…...

眨个眼就学会了PixiJS
本文简介 带尬猴,我是德育处主任 当今的Web开发中,图形和动画已经成为了吸引用户注意力的重要手段之一。而 Pixi.js 作为一款高效、易用的2D渲染引擎,已经成为了许多开发者的首选(我吹的)。本文将为工友们介绍PixiJS的…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...

嵌入式学习笔记DAY33(网络编程——TCP)
一、网络架构 C/S (client/server 客户端/服务器):由客户端和服务器端两个部分组成。客户端通常是用户使用的应用程序,负责提供用户界面和交互逻辑 ,接收用户输入,向服务器发送请求,并展示服务…...
