深度学习:激活函数曲线总结
深度学习:激活函数曲线总结
在深度学习中有很多时候需要利用激活函数进行非线性处理,在搭建网路的时候也是非常重要的,为了更好的理解不同的激活函数的区别和差异,在这里做一个简单的总结,在pytorch中常用的激活函数的数学表达形式,同时为了更直观的感受,给出不同激活函数的曲线形式,方便查询。
import torch
import torch.nn as nn
x = torch.linspace(-4, 4, 400) # 在-4和4之间画400个点。
1. nn.leakyReLU()
给负值一个斜率,不全为零。
- 数学公式:
LeakyReLU ( x ) = { x , if x ≥ 0 negative_slope × x , otherwise \text{LeakyReLU}(x) = \begin{cases} x, & \text{ if } x \geq 0 \\ \text{negative\_slope} \times x, & \text{ otherwise } \end{cases} LeakyReLU(x)={x,negative_slope×x, if x≥0 otherwise
leakyrelu = nn.LeakyReLU(negative_slope=0.01)
negative_slope 是一个小于1的值,通常设置为0.01,用于控制在输入小于0时的输出斜率。这意味着在nn.LeakyReLU中,负数输入会乘以negative_slope,而正数输入保持不变。
- 对应曲线:

2. nn.Relu()
ReLU是一个常用的激活函数,它将负数值设为0,保持正数值不变。
- 数学公式:
ReLU ( x ) = ( x ) + = max ( 0 , x ) \text{ReLU}(x) = (x)^+ = \max(0, x) ReLU(x)=(x)+=max(0,x)
relu = nn.ReLU()
- 函数曲线:

3. nn.Tanh()
Tanh函数将输入映射到-1和1之间
- 数学公式
Tanh ( x ) = tanh ( x ) = exp ( x ) − exp ( − x ) exp ( x ) + exp ( − x ) \text{Tanh}(x) = \tanh(x) = \frac{\exp(x) - \exp(-x)} {\exp(x) + \exp(-x)} Tanh(x)=tanh(x)=exp(x)+exp(−x)exp(x)−exp(−x)
Tanh = nn.Tanh()
- 函数曲线

4. nn.PReLU()
PReLU是具有可学习参数的激活函数,用于克服ReLU的一些问题
- 数学公式
RReLU ( x ) = { x if x ≥ 0 a x otherwise \text{RReLU}(x) = \begin{cases} x & \text{if } x \geq 0 \\ ax & \text{ otherwise } \end{cases} RReLU(x)={xaxif x≥0 otherwise
PReLU = nn.PReLU(num_parameters=1)
- 函数曲线

5. nn.ELU()
所有点上都是连续的和可微的,训练快
- 数学公式:
ELU ( x ) = { x , if x > 0 α ∗ ( exp ( x ) − 1 ) , if x ≤ 0 \text{ELU}(x) = \begin{cases} x, & \text{ if } x > 0\\ \alpha * (\exp(x) - 1), & \text{ if } x \leq 0 \end{cases} ELU(x)={x,α∗(exp(x)−1), if x>0 if x≤0
ELU = nn.ELU()
- 函数曲线

6. nn.SELU()
- 数学公式:
SELU ( x ) = scale ∗ ( max ( 0 , x ) + min ( 0 , α ∗ ( exp ( x ) − 1 ) ) ) \text{SELU}(x) = \text{scale} * (\max(0,x) + \min(0, \alpha * (\exp(x) - 1))) SELU(x)=scale∗(max(0,x)+min(0,α∗(exp(x)−1)))
SELU = nn.SELU()
- 函数曲线:

7. nn.GELU()
- 数学公式:
GELU ( x ) = x ∗ Φ ( x ) \text{GELU}(x) = x * \Phi(x) GELU(x)=x∗Φ(x)
GELU = nn.GELU()
- 函数曲线:

8. nn.Mish()
- 数学公式:
Mish ( x ) = x ∗ Tanh ( Softplus ( x ) ) \text{Mish}(x) = x * \text{Tanh}(\text{Softplus}(x)) Mish(x)=x∗Tanh(Softplus(x))
Mish = nn.Mish()
- 函数曲线:

9 . nn.Softmax()
- 数学公式:
Softmax ( x i ) = exp ( x i ) ∑ j exp ( x j ) \text{Softmax}(x_{i}) = \frac{\exp(x_i)}{\sum_j \exp(x_j)} Softmax(xi)=∑jexp(xj)exp(xi)
Softmax = nn.Softmax()
y = Softmax(x)
- 函数曲线:

总结
感觉还是看曲线的形状,把大体的形状记住更直观些。
相关文章:

深度学习:激活函数曲线总结
深度学习:激活函数曲线总结 在深度学习中有很多时候需要利用激活函数进行非线性处理,在搭建网路的时候也是非常重要的,为了更好的理解不同的激活函数的区别和差异,在这里做一个简单的总结,在pytorch中常用的激活函数的…...

Elasticsearch-06-Elasticsearch Java API Client
前言 简介 在 Elasticsearch7.15版本之后,Elasticsearch官方将它的高级客户端 RestHighLevelClient标记为弃用状态。同时推出了全新的 Java API客户端 Elasticsearch Java API Client,该客户端也将在 Elasticsearch8.0及以后版本中成为官方推荐使用的客…...

计算机网络第3章-运输层(2)
可靠数据传输原理 可靠数据传输依靠数据在一条可靠信道上进行传输。 TCP也正是依靠可靠信道进行传数据,从而数据不会被丢失。 而实现这种可靠数据传输服务是可靠数据传输协议的责任 构造可靠数据传输协议 1.经完全可靠信道的可靠数据传输:rdt1.0 在…...
【微信小程序】实现投票功能(附源码)
一、Vant Weapp介绍 Vant Weapp 是一个基于微信小程序的组件库,它提供了丰富的 UI 组件和交互功能,能够帮助开发者快速构建出现代化的小程序应用。Vant Weapp 的设计理念注重简洁、易用和高效,同时提供灵活的定制化选项,以满足开发…...
Pytorch入门实例的分解写法
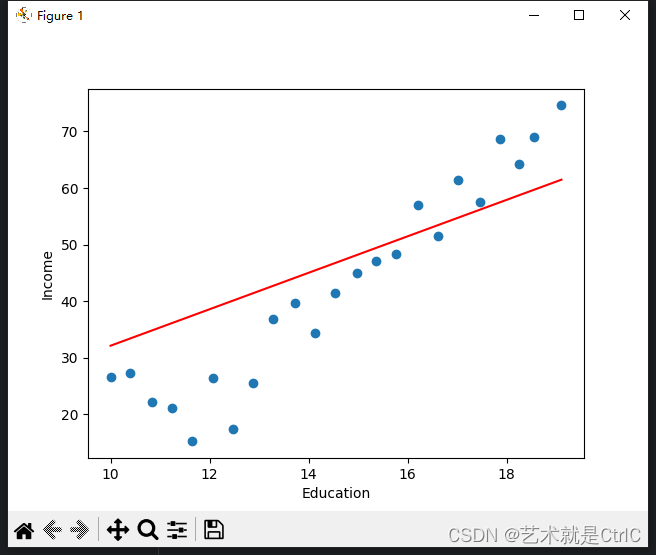
数据集是受教育年限和收入,如下图 代码如下 import torch import numpy as np import matplotlib.pyplot as plt import pandas as pddata pd.read_csv(./Income.csv)X torch.from_numpy(data.Education.values.reshape(-1,1).astype(np.float32)) Y torch.from_numpy(data…...
)
Google单元测试sample分析(一)
本文开始从googletest提供的sample案例分析如何使用单元测试, 代码路径在googletest/googletest/samples/sample1.unittest.cc 本文件主要介绍EXPECT*相关宏使用 EXPECT_EQ 判断是否相等 EXPECT_TRUE 是否为True EXPECT_FALSE 是否为False TEST(FactorialTest, N…...

requests 实践
Requests 常用参数 method: 请求方式 get,或者 post,put,delete 等 url : 请求的 url 地址 接口文档标注的接口请求地址 params:请求数据中的链接,常见的一个 get 请求,请求参数都是在 url 地址…...

UI设计公司成长日记2:修身及持之以恒不断学习是要务
作者:蓝蓝设计 要做一个好的UI设计公司,不仅要在能力上设计能力一直(十几年几十年)保持优秀稳定的保持输出,以及心态的平和宽广。创始人对做公司要有信心,合伙人之间要同甘共苦,遵守规则,做好表…...
辅助驾驶功能开发-功能规范篇(23)-2-Mobileye NOP功能规范
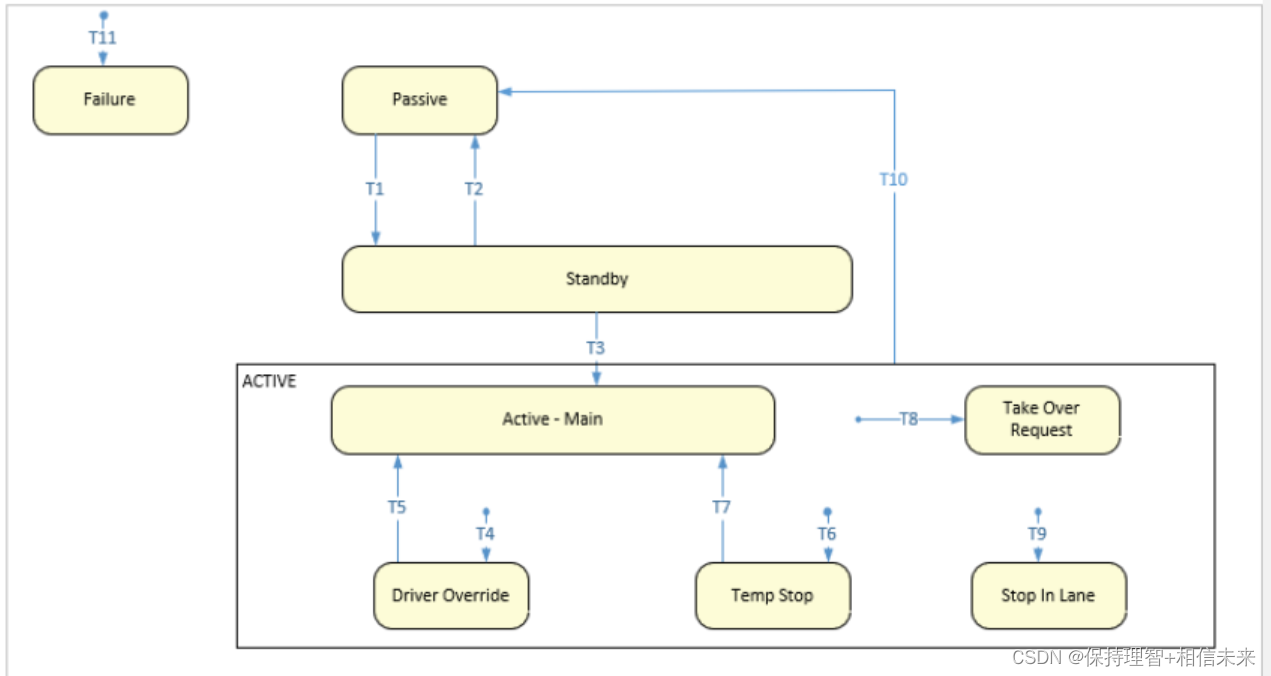
5.2 状态机要求 5.2.1 NOP/HWP 状态机 NOP/HWP状态机如下所示: 下表总结了这些状态: 状态描述Passive不满足功能条件,功能无法控制车辆执行器。Standby满足功能条件。该功能不是由驾驶员激活的。功能不控制车辆执行器。Active - Main功能由驾驶员激活。功能是控制…...

React中如何提高组件的渲染效率
一、是什么 react 基于虚拟 DOM 和高效 Diff算法的完美配合,实现了对 DOM最小粒度的更新,大多数情况下,React对 DOM的渲染效率足以我们的业务日常 复杂业务场景下,性能问题依然会困扰我们。此时需要采取一些措施来提升运行性能&…...
)
springboot+mybatis3.5.2动态查询某一字段在某一段时间内的统计信息(折线图)
需求: 动态查询某一统计字段在一段时间内的统计折线图信息 controller层 ApiOperation(value "getStatisticDetail", notes "统计折线图")GetMapping("/detail")ResponseStatus(HttpStatus.OK)AccessLogAnnotation(ignoreRequestA…...
关于本地项目上传到gitee的详细流程
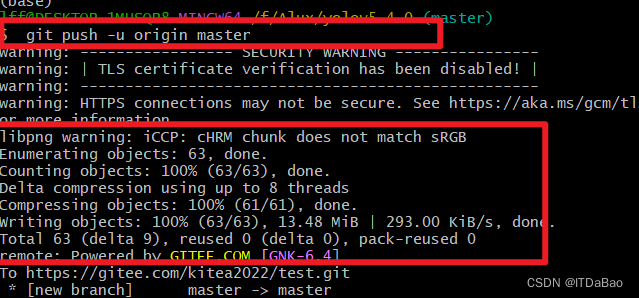
如何上传本地项目到Gitee的流程: 1.Gitee创建项目 2. 进入所在文件夹,右键点击Git Bash Here 3.配置用户名和邮箱 在gitee的官网找到命令,注意这里的用户名和邮箱一定要和你本地的Git相匹配,否则会出现问题。 解决方法如下&…...

MarkDown详细入门笔记
本帖整理了MarkDown的入门学习笔记~ 一.介绍 Markdown 是一种轻量级的「标记语言」,它的优点很多,目前也被越来越多的写作爱好者,撰稿者广泛使用。 诸如微信公众平台、CSDN博客、还有Typora中写文档的部分,均涉及到MD的功能~ 它…...

算法——贪心算法
贪心算法(Greedy Algorithm)是一种算法设计策略,通常用于解决组合优化问题,其核心思想是在每一步都选择当前状态下最优的解,而不考虑之后的步骤。贪心算法在每一步都做出局部最优选择,期望通过一系列局部最…...

102.linux5.15.198 编译 firefly-rk3399(1)
1. 平台: rk3399 firefly 2g16g 2. 内核:linux5.15.136 (从内核镜像网站下载) 3. 交叉编译工具 gcc version 7.5.0 (Ubuntu/Linaro 7.5.0-3ubuntu1~18.04) 4. 宿主机:ubuntu18.04 5. 需要的素材和资料ÿ…...

易点易动固定资产管理系统:多种盘点方式助力年终固定资产盘点
年末固定资产盘点是企业管理中一项重要而繁琐的任务。为了帮助企业高效完成年终固定资产盘点工作,易点易动固定资产管理系统提供了多种盘点方式。本文将详细介绍易点易动固定资产管理系统的多种盘点方式,展示如何借助该系统轻松完成年终固定资产盘点&…...
C# Winform编程(10)Chart图表控件
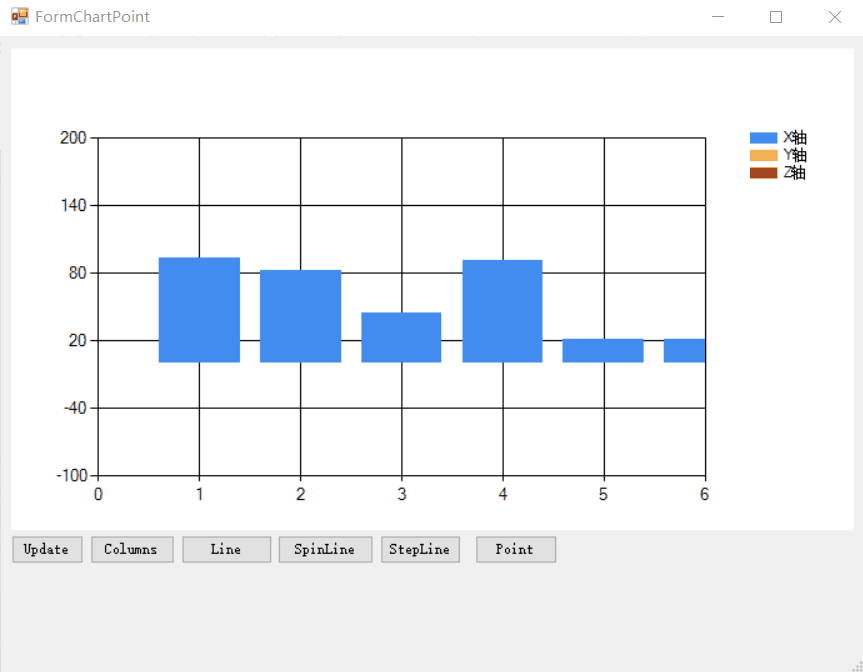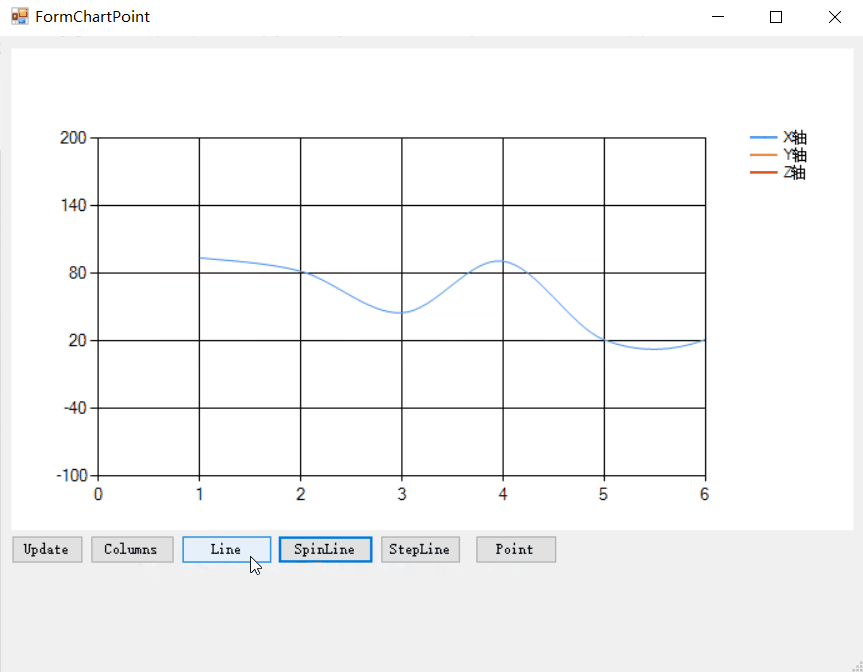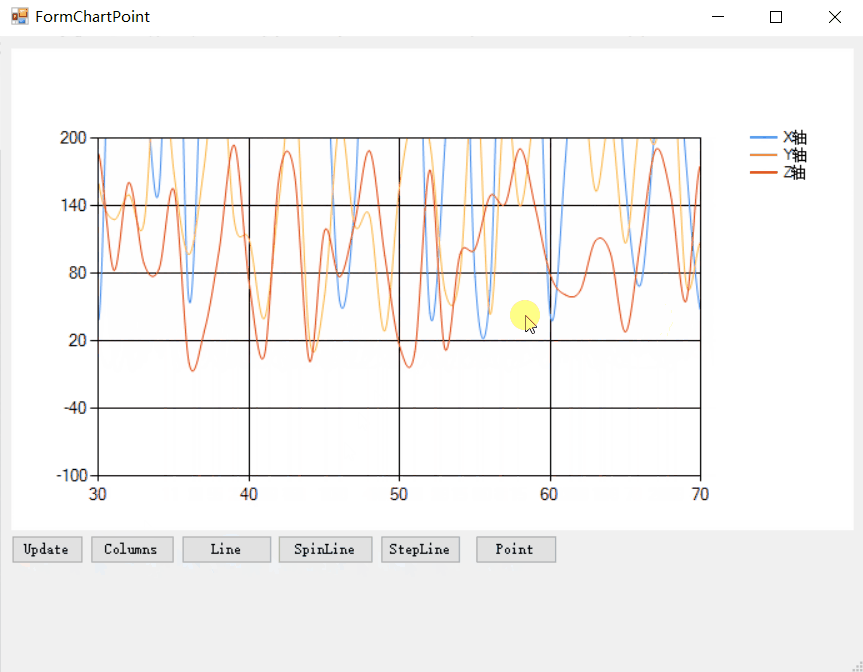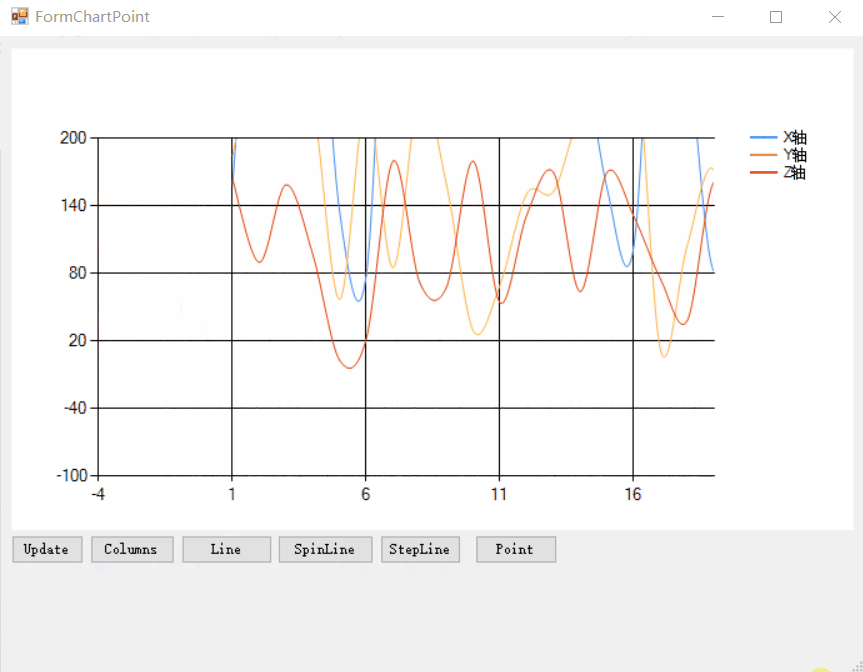
Chart控件 Chart控件Chart属性详述Chart属性设置图表样式属性数据样式属性图例样式图标区样式SeriesChartType类型 Chart控件鼠标滚轮事件特殊处理Series绑定数据演示代码鼠标滚轮缩放图表示例参考引用 Chart控件 Chart控件是微软自带的一种图形可视化组件,使用简单…...
|如何做新品上市满意度调研)
群狼调研(长沙产品概念测试)|如何做新品上市满意度调研
新品上市满意度调研是一种重要的市场研究方法,它通过收集和分析消费者对新产品的态度、购买意愿和满意度等方面的数据,帮助企业了解消费者的需求和期望,发现新产品的问题和不足,从而为产品改进提供有力的数据支持。群狼调研&#…...

Lua与C++交互
文章目录 1、Lua和C交互2、基础练习2.1、加载Lua脚本并传递参数2.2、加载脚本到stable(包)2.3、Lua调用c语言接口2.4、Lua实现面向对象2.5、向脚本中注册c的类 1、Lua和C交互 1、lua和c交互机制是基于一个虚拟栈,C和lua之间的所有数据交互都通…...

Ubuntu安装pyenv,配置虚拟环境
文章目录 安装pyenvpyenv创建虚拟环境一般情况下创建虚拟环境的方法 安装pyenv 摘自:文章 pyenv可以管理不同的python版本 1、安装pyenv的依赖库 # 执行以下命令安装依赖库 # 更新源 sudo apt-get update # 更新软件 sudo apt-get upgradesudo apt-get install ma…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

MySQL 索引底层结构揭秘:B-Tree 与 B+Tree 的区别与应用
文章目录 一、背景知识:什么是 B-Tree 和 BTree? B-Tree(平衡多路查找树) BTree(B-Tree 的变种) 二、结构对比:一张图看懂 三、为什么 MySQL InnoDB 选择 BTree? 1. 范围查询更快 2…...

windows系统MySQL安装文档
概览:本文讨论了MySQL的安装、使用过程中涉及的解压、配置、初始化、注册服务、启动、修改密码、登录、退出以及卸载等相关内容,为学习者提供全面的操作指导。关键要点包括: 解压 :下载完成后解压压缩包,得到MySQL 8.…...
