【随机过程】布朗运动
这里写目录标题
- Brownian motion
Brownian motion
The brownian motion 1D and brownian motion 2D functions, written with the cumsum command and without for loops, are used to generate a one-dimensional and two-dimensional Brownian motion, respectively.
使用cumsum命令编写的布朗运动1D函数和不带for循环的布朗运动2D函数分别生成一维和二维布朗运动。
These Wiener processes are characterized by normal-centered increments with variance h, where h is the time increment, generated by the command randn(1,n)*sqrt(h).
这些维纳过程的特征是方差为h的正态中心增量,其中h是时间增量,由命令randn(1,n)*sqrt(h)生成。
We consider a time interval T = 1000, divided into n = 1000 increments of value h = 1.
我们考虑一个时间间隔T = 1000,分成n = 1000个值h = 1的增量。
Figure1 shows, for example, two trajectories W(t) of a one-dimensional Wiener process.
例如,图1显示了一维维纳过程的两条轨迹W(t)。
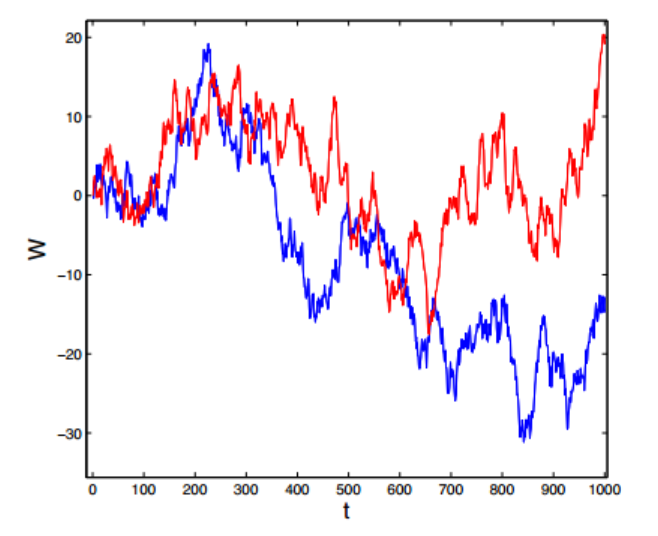 Figure 1 { Two examples of trajectories as a function of the time t of a Wiener process W(t) in one
Figure 1 { Two examples of trajectories as a function of the time t of a Wiener process W(t) in one
dimension.
图1{两个关于一维维纳过程W(t)时间t的轨迹函数的例子。
Figure 2,on the other hand, shows two examples of a two-dimensional Brownian motion trajectory, this time as a function of the X and Y spatial coordinates.
另一方面,图2显示了两个二维布朗运动轨迹的例子,这一次是X和Y空间坐标的函数。
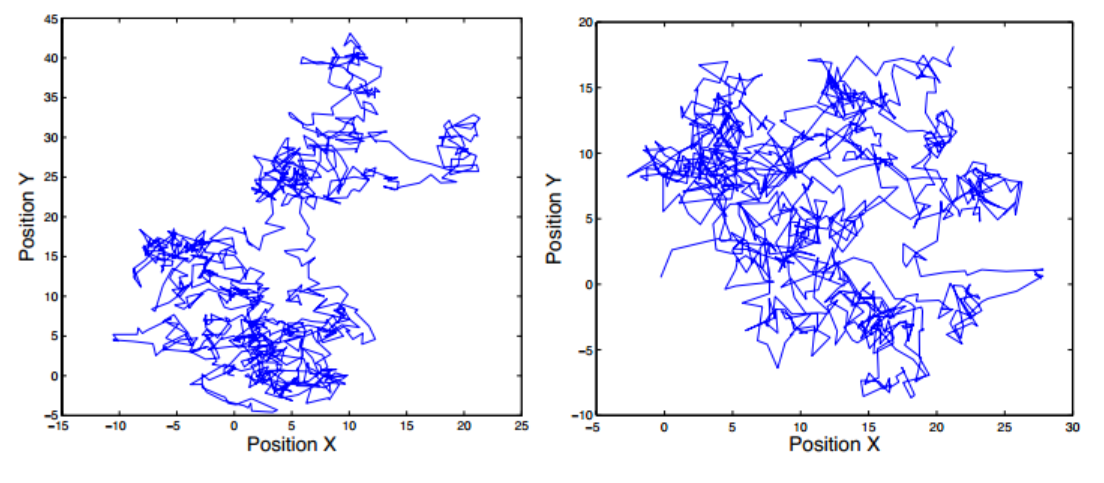
Figure 2 -Two examples of trajectories of a two dimensional Wiener process in the plane XY .
图2-在XY平面上二维维纳过程的轨迹的两个例子。
Given N (number of steps), M (number of trajectories) and T (maximum of the time interval),
we generate a matrix W all containing M trajectories of the Brownian motion in one dimension
on the interval [0; T] with a discretization step h = T=N.
给定N(步数),M(轨迹数)和T(时间间隔的最大值),我们生成一个矩阵W,其中包含布朗运动在一维中的M个轨迹,在区间[0;T],离散步长h = T=N。
Figure 3 shows M = 10; 100; 1000 trajectories over the interval [0; 10] with N = 1000 steps.
图3显示M = 10;100;在区间[0;10] N = 1000步。
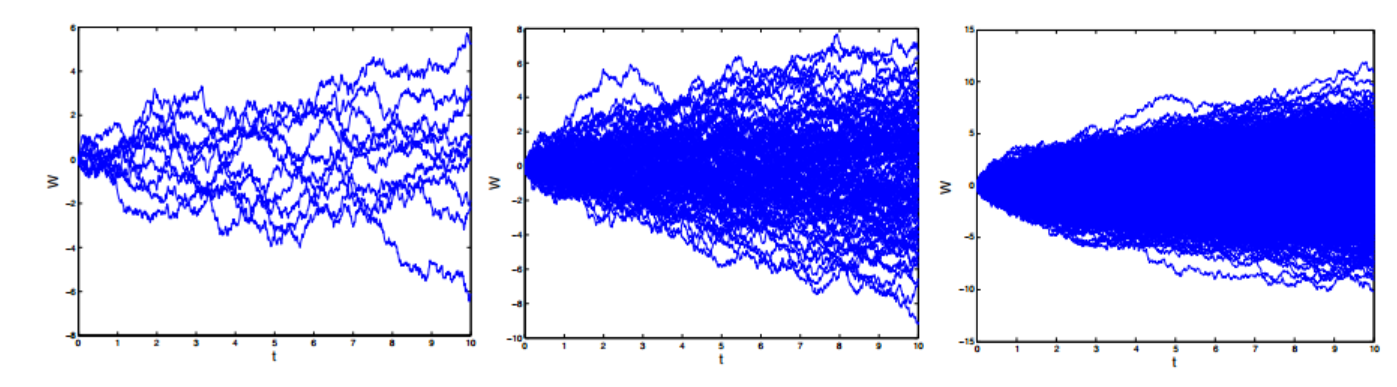
Figure 3 { M = 10; 100; 1000 (from left to right) trajectories of a one-dimensional Wiener process
over the time interval [0; 10] with N = 1000 discretisation steps.
图3 {M = 10;100;1000个(从左到右)一维维纳过程在时间区间[0;10], N = 1000离散步长。
We simulate M = 1000 trajectories over the interval [0; 10]. Figure 4 shows the mean and
the variance over time of these trajectories.
我们在区间[0;10]。图4显示了这些轨迹随时间的平均值和方差。

Figure 4 { Mean and variance of M = 1000 trajectories of a Brownian motion in one dimension.
图4 {M = 1000条布朗运动轨迹在一维中的均值和方差。
In contrast, figure 5 shows the expectation valuesE[W(t)], E[W(t)2] et E[W(t)4] obtained numerically as a function of time.
与此相反,图5给出了期望值E[W(t)]、E[W(t) 2]和E[W(t) 4]作为时间函数的数值计算结果。
The first moment corresponds exactly to the average.
第一个力矩正好对应于平均值。
In the presence of a zero mean, the variance is equivalent to the moment E[W(t)2].
在均值为零的情况下,方差等于矩E[W(t) 2]。
The red lines in each panel of Figure 5 show that the equalities E[W(t)] = 0, E[W(t)2] = t, and E[W(t)4] = 3t2 are satisfied.
图5中每个面板中的红线表示满足等式E[W(t)] = 0、E[W(t) 2] = t和E[W(t) 4] = 3t 2。
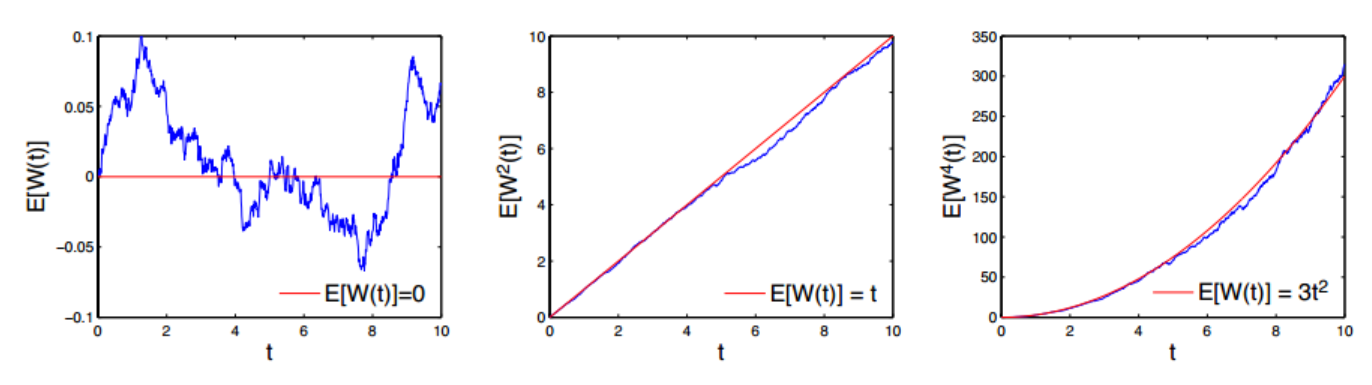 Figure 5 { Expectation values E[W(t)], E[W(t)2] and E[W(t)4] calculated numerically and compared with the curves (in red) expected theoretically.
Figure 5 { Expectation values E[W(t)], E[W(t)2] and E[W(t)4] calculated numerically and compared with the curves (in red) expected theoretically.
图5{数值计算的期望值E[W(t)]、E[W(t) 2]、E[W(t) 4]与理论期望曲线(红色)对比。
相关文章:

【随机过程】布朗运动
这里写目录标题 Brownian motion Brownian motion The brownian motion 1D and brownian motion 2D functions, written with the cumsum command and without for loops, are used to generate a one-dimensional and two-dimensional Brownian motion, respectively. 使用cu…...

基于机器视觉的车道线检测 计算机竞赛
文章目录 1 前言2 先上成果3 车道线4 问题抽象(建立模型)5 帧掩码(Frame Mask)6 车道检测的图像预处理7 图像阈值化8 霍夫线变换9 实现车道检测9.1 帧掩码创建9.2 图像预处理9.2.1 图像阈值化9.2.2 霍夫线变换 最后 1 前言 🔥 优质竞赛项目系列,今天要分…...

C语言文件读写,文件相关操作
文章目录 C语言文件读写,文件相关操作1.C语言万物皆是地址,文件读操作2.文件的写3.文件的复制4.获取文件的大小5.文件的加密解密 C语言文件读写,文件相关操作 1.C语言万物皆是地址,文件读操作 // // Created by MagicBook on 20…...
竞赛选题 深度学习卷积神经网络的花卉识别
文章目录 0 前言1 项目背景2 花卉识别的基本原理3 算法实现3.1 预处理3.2 特征提取和选择3.3 分类器设计和决策3.4 卷积神经网络基本原理 4 算法实现4.1 花卉图像数据4.2 模块组成 5 项目执行结果6 最后 0 前言 🔥 优质竞赛项目系列,今天要分享的是 基…...

CMake教程 - basic point
CMake教程 - basic point 1 - Building a Basic Project 最基本的CMake项目是由单个源代码文件构建的可执行文件。对于像这样简单的项目,只需要一个带有三个命令的CMakeLists.txt文件。 注意:尽管CMake支持大写、小写和混合大小写命令,但小…...
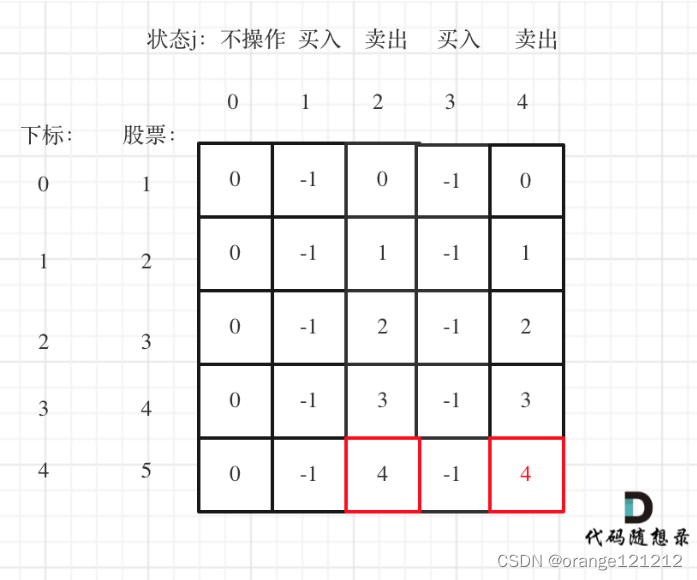
day52--动态规划11
想死,但感觉死的另有其人,,怎么还在动态规划!!!!! 123.买卖股票的最佳时机III 188.买卖股票的最佳时机IV 第一题:买卖股票的最佳时机III 给定一个数组,它…...

Jenkins入门级安装部署
前言 Jenkins是一个开源软件项目,是基于Java开发的一种持续集成工具,用于监控持续重复的工作,旨在提供一个开放易用的软件平台,使软件项目可以进行持续集成。通常,项目中常用Jenkins作为编译打包项目的工具࿰…...

tcpdump 异常错误
tcpdump 进行抓包的时候,-w 提示 Permission denied: sudo tcpdump -w test1.log tcpdump: test1.log: Permission denied 开始以为是用户权限的问题,后来换用 root 账户还是不行,经搜索,是 AppArmor 的问题。 解决方…...
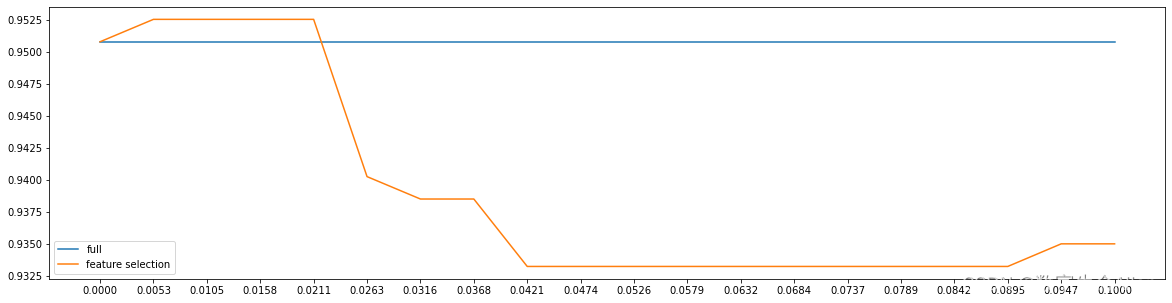
如何绘制【逻辑回归】中threshold参数的学习曲线
threshold参数的意义是通过筛选掉低于threshold的参数,来对逻辑回归的特征进行降维。 首先导入相应的模块: from sklearn.linear_model import LogisticRegression as LR from sklearn.datasets import load_breast_cancer from sklearn.model_selecti…...

4.1 数据库安全性概述
思维导图: 前言: - **第一章回顾**:数据库特点 - 统一的数据保护功能,确保数据安全、可靠、正确有效。 - 数据保护主要涵盖: 1. **数据的安全性**(本章焦点) 2. 数据的完整性(第…...
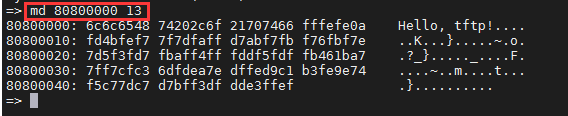
tftp服务的搭建
TFTP服务的搭建 1 先更新一下apt包 sudo apt-get update2 服务器端(虚拟机上)安装 TFTP相关软件 sudo apt-get install xinetd tftp tftpd -y3 创建TFTP共享目录 mkdir tftp_sharetftp_shaer的路径是/home/cwz/tftp_share 3.1 修改共享目录的权限 sudo chmod -R 777 tftp…...

c语言简介
C 语言最初是作为 Unix 系统的开发工具而发明的。 1969年,美国贝尔实验室的肯汤普森(Ken Thompson)与丹尼斯里奇(Dennis Ritchie)一起开发了 Unix 操作系统。Unix 是用汇编语言写的,无法移植到其他计算机&…...
OpenLayers.js 入门教程:打造互动地图的入门指南
本文简介 戴尬猴,我是德育处主任 本文介绍如何使用 OpenLayers.js (后面简称 ol)。ol 是一个开源 JavaScript 库,可用于在Web页面上创建交互式地图。 ol能帮助我们在浏览器轻松地使用地图功能,例如地图缩放、地图拖动…...
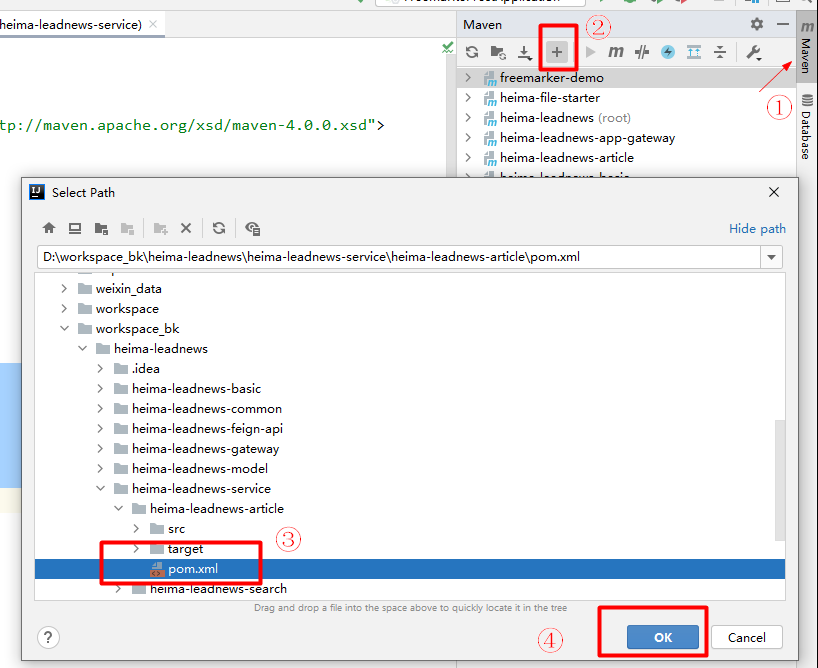
黑马头条:app端文章查看
黑马头条:app端文章查看 黑马头条:app端文章查看文章列表加载1. 需求分析2. 表结构分析3. 导入文章数据库3.1 导入数据库3.2 导入对应的实体类 4. 实现思路5. 接口定义6. 功能实现6.1:导入heima-leadnews-article微服务,资料在当天…...
)
常见使用总结篇(一)
Autowired和Resource注解的区别 Autowired注解是Spring提供的,Resource注解是J2EE本身提供Autowird注解默认通过byType方式注入(没有匹配会通过byName方式),而Resource注解默认通过byName方式注入(没有匹配会通过byType方式)Autowired注解注入的对象需要…...

【软考系统架构设计师】2023年系统架构师冲刺模拟习题之《数据库系统》
在数据库章节中可能会考察以下内容: 文章目录 数据库完整性约束🌟数据库模式🌟🌟ER模式🌟关系代数🌟🌟并发控制🌟数据仓库与数据挖掘🌟🌟反规范化技术&#x…...
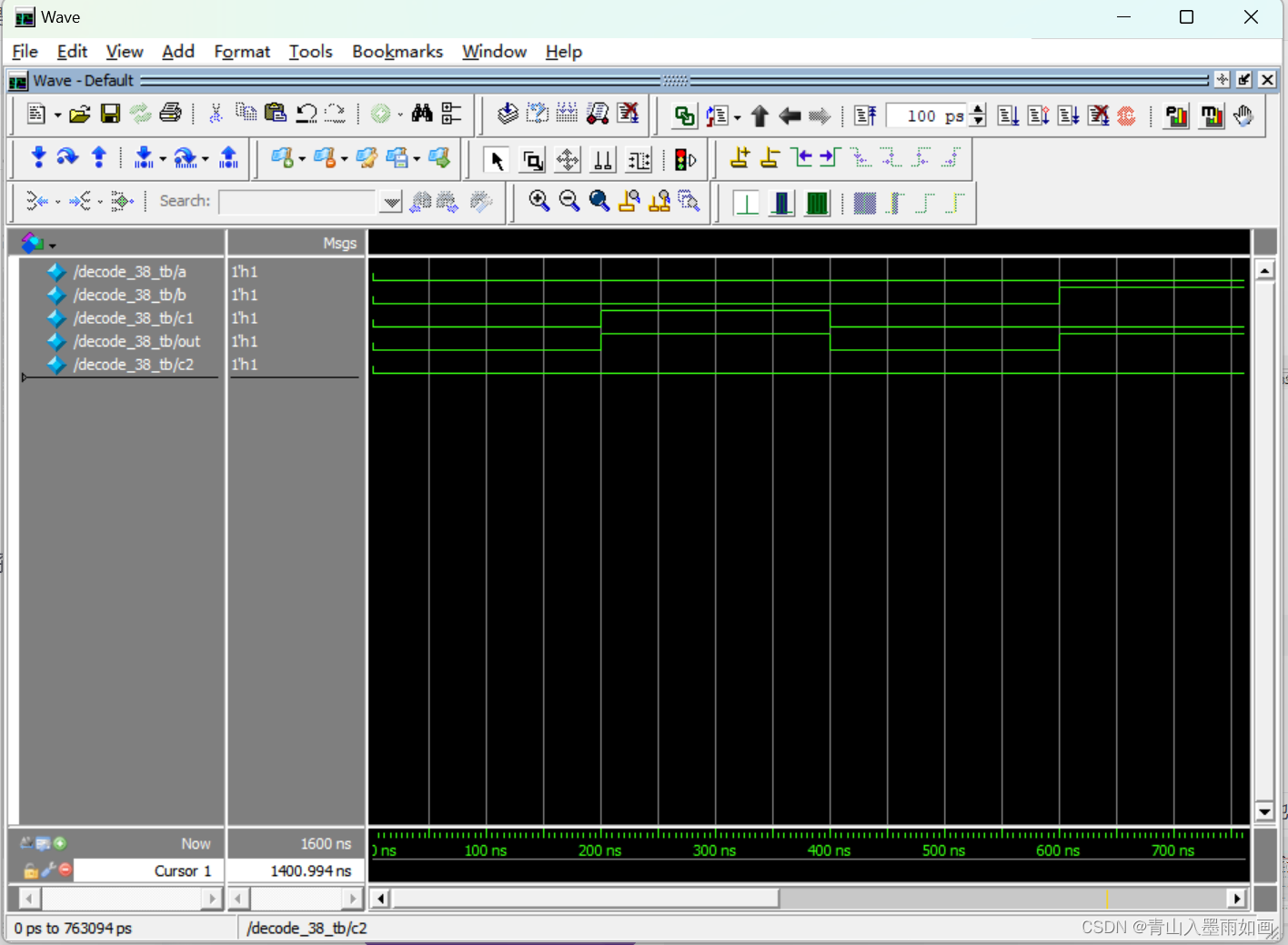
北邮22级信通院数电:Verilog-FPGA(7)第七周实验(1):带使能端的38译码器全加器(关注我的uu们加群咯~)
北邮22信通一枚~ 跟随课程进度更新北邮信通院数字系统设计的笔记、代码和文章 持续关注作者 迎接数电实验学习~ 获取更多文章,请访问专栏: 北邮22级信通院数电实验_青山如墨雨如画的博客-CSDN博客 关注作者的uu们可以进群啦~ 目录 方法一ÿ…...

SIT3491ISO具有隔离功能,256 节点,全双工 RS422/RS485 芯片
SIT3491ISO 是一款电容隔离的全双工 RS-422/485 收发器,总线端口 ESD 保护能力 HBM 达到 15kV 以上,功能完全满足 EIA-422 以及 TIA/EIA-485 标准要求的 RS-422/485 收发器。 SIT3491ISO 包括一个驱动器和一个接收器,两者均…...
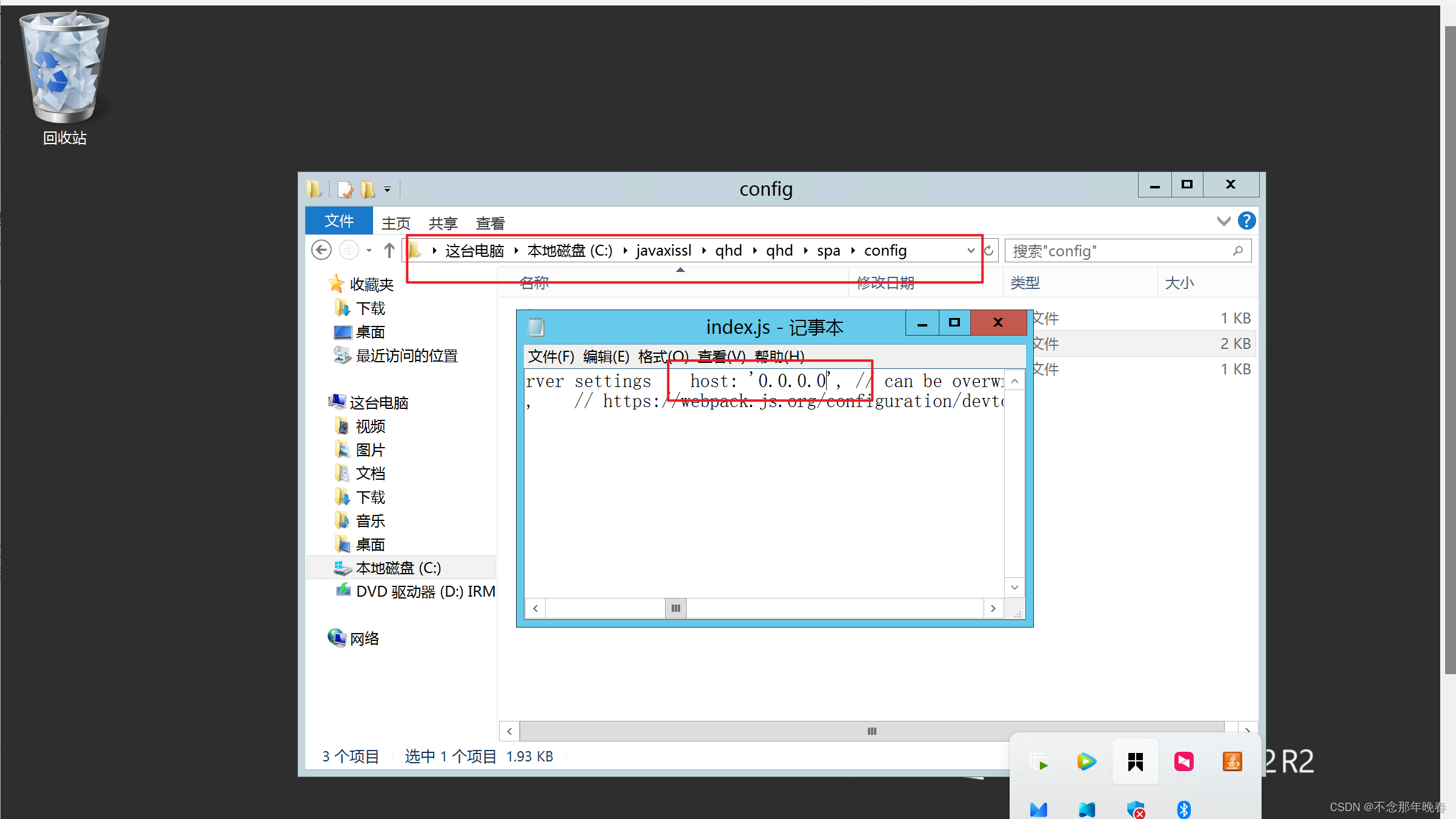
在windows服务器上部署一个单机项目以及前后端分离项目
目录 一. 单机项目在windows服务器上的部署 1.1 在本机上测试项目无误 1.1.1 在数据库中测试sql文件没问题 1.1.2 在tomcat中测试war文件无误 1.1.3 测试完成后,进入浏览器运行单机项目确保无误 1.2 在windows服务器中运行项目 二. 前后端分离项目在服务器上…...
)
使用jdbc技术,在数据库中存储大数据对象(使用字节IO流读取图片等给blob等二进制类型数据赋值)
在MySQL中,BLOB是一种数据类型,代表二进制大对象(Binary Large Object),可以存储大量的二进制数据,如图像、声音、视频等。BLOB类型的数据在存储和检索时会以二进制方式进行处理,而不是字符方式…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...
