day52--动态规划11
想死,但感觉死的另有其人,,怎么还在动态规划!!!!!
- 123.买卖股票的最佳时机III
- 188.买卖股票的最佳时机IV
第一题:买卖股票的最佳时机III
给定一个数组,它的第 i 个元素是一支给定的股票在第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你最多可以完成 两笔 交易。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
-
示例 1:
-
输入:prices = [3,3,5,0,0,3,1,4]
-
输出:6 解释:在第 4 天(股票价格 = 0)的时候买入,在第 6 天(股票价格 = 3)的时候卖出,这笔交易所能获得利润 = 3-0 = 3 。随后,在第 7 天(股票价格 = 1)的时候买入,在第 8 天 (股票价格 = 4)的时候卖出,这笔交易所能获得利润 = 4-1 = 3。
就是说对于这个股票,只能进行最多四次操作,买了卖了然后再买再卖
动规五部曲
(1)确定dp数组以及下标的含义
一天可以发生5种情况
0. 没有操作
1.第一次持有股票
2.第一次不持有股票
3.第二次持有股票
4.第二次不持有股票
这里还是使用二维数组,但是之前只有dp[i][0]和dp[i][1]两种情况,这里dp[i][j]中表示第i天,j为[0-4]共5个状态,dp[i][j]表示第i天状态j所剩最大现金。
(2)确定递推公式
达到dp[i][1]状态,有两个具体的操作:
操作一:第i天买入股票,那么dp[i][1]=dp[i-1][0]-prices[i]
操作二:第i天没有操作,dp[i][1]=dp[i-1][1]
dp[i][1]=max(dp[i-1][0]-prices[i], dp[i-1][1]);还是取最大的情况
dp[i][2]也有两种具体操作:
操作一:第i天卖出了股票,那么dp[i][2]=dp[i-1][1]+prices[i]
操作二:第i天没有卖出股票,跟前一天一样,dp[i][2]=dp[i-1][2]
同理,dp[i][2]=max(dp[i-1][1]+prices[i], dp[i-1][2]);
同上 dp[i][3]和dp[i][4]一样的计算方法
(3)dp数组如何初始化
第0天没有操作,即dp[0][0]=0
第0天做第一次买入的操作,即dp[0][1]=-prices[0]
第0天做第一次卖出的操作,因为没有股票,所以没有卖出的东西,dp[0][2]=0
同理,第二次买进卖出: dp[0][3]=-prices[0]; dp[0][4]=0
(4)确定遍历顺序
从前向后遍历
(5)举例推导dp数组
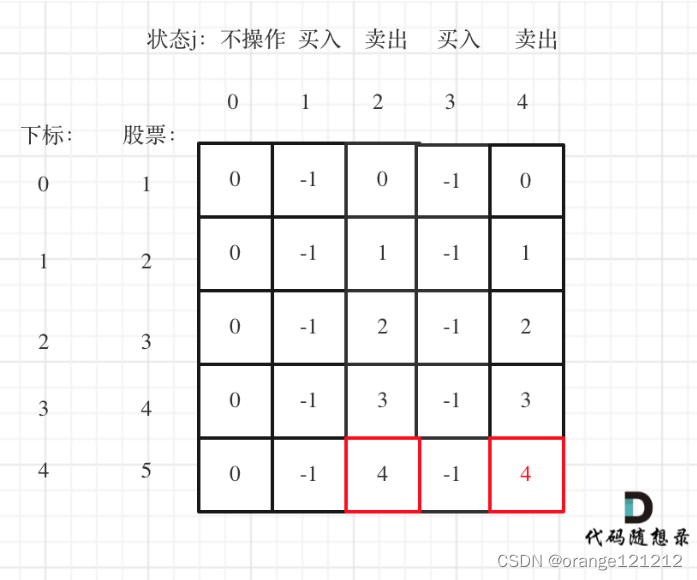
似乎有一些理解了:之前只能买进卖出各一次,所以对于i天来说,可以买进,或者卖出,dp[i][0]就是买进操作,dp[i][1]就是卖出操作,最后求出最大的值
第二题:买卖股票的最佳时机IV
给定一个整数数组 prices ,它的第 i 个元素 prices[i] 是一支给定的股票在第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你最多可以完成 k 笔交易。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
-
示例 1:
-
输入:k = 2, prices = [2,4,1]
-
输出:2 解释:在第 1 天 (股票价格 = 2) 的时候买入,在第 2 天 (股票价格 = 4) 的时候卖出,这笔交易所能获得利润 = 4-2 = 2。
相比上一题,k成了可变的;
也就是进行k此买进,k次卖出;
其他规则和上题一样:
只要dp[i][j]的下标有了新的意义,int j=0;j<2*k-1;j++
为什么呢,因为k次交易,就一共是2k次动作,每一次都可以买(卖)或者不操作
//首先dp[0][0]不做操作为0//然后dp[0][1]表示第一次买进//dp[0][3]表示第二次买进,前面可能都没有操作,所以“第一次”买进的时候,钱为-prices[0];for(int j=1;j<2*k;j+=2){ dp[0][j]=-prices[0];}相关文章:

day52--动态规划11
想死,但感觉死的另有其人,,怎么还在动态规划!!!!! 123.买卖股票的最佳时机III 188.买卖股票的最佳时机IV 第一题:买卖股票的最佳时机III 给定一个数组,它…...

Jenkins入门级安装部署
前言 Jenkins是一个开源软件项目,是基于Java开发的一种持续集成工具,用于监控持续重复的工作,旨在提供一个开放易用的软件平台,使软件项目可以进行持续集成。通常,项目中常用Jenkins作为编译打包项目的工具࿰…...

tcpdump 异常错误
tcpdump 进行抓包的时候,-w 提示 Permission denied: sudo tcpdump -w test1.log tcpdump: test1.log: Permission denied 开始以为是用户权限的问题,后来换用 root 账户还是不行,经搜索,是 AppArmor 的问题。 解决方…...
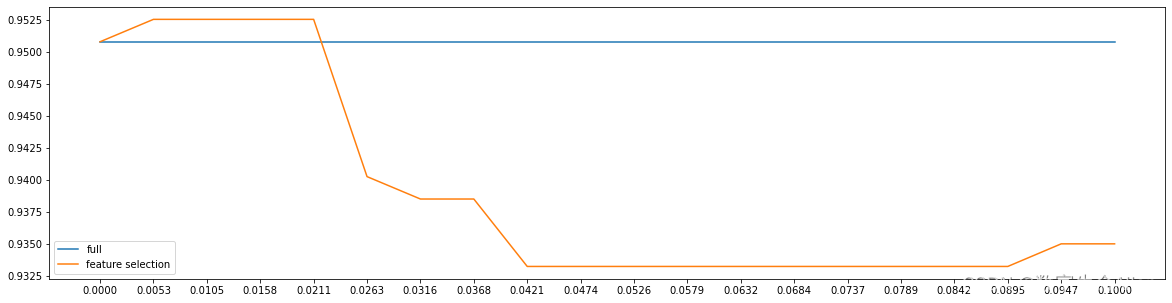
如何绘制【逻辑回归】中threshold参数的学习曲线
threshold参数的意义是通过筛选掉低于threshold的参数,来对逻辑回归的特征进行降维。 首先导入相应的模块: from sklearn.linear_model import LogisticRegression as LR from sklearn.datasets import load_breast_cancer from sklearn.model_selecti…...

4.1 数据库安全性概述
思维导图: 前言: - **第一章回顾**:数据库特点 - 统一的数据保护功能,确保数据安全、可靠、正确有效。 - 数据保护主要涵盖: 1. **数据的安全性**(本章焦点) 2. 数据的完整性(第…...
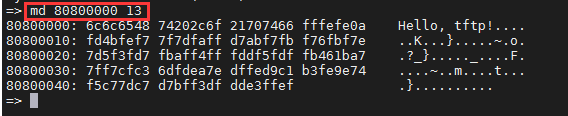
tftp服务的搭建
TFTP服务的搭建 1 先更新一下apt包 sudo apt-get update2 服务器端(虚拟机上)安装 TFTP相关软件 sudo apt-get install xinetd tftp tftpd -y3 创建TFTP共享目录 mkdir tftp_sharetftp_shaer的路径是/home/cwz/tftp_share 3.1 修改共享目录的权限 sudo chmod -R 777 tftp…...

c语言简介
C 语言最初是作为 Unix 系统的开发工具而发明的。 1969年,美国贝尔实验室的肯汤普森(Ken Thompson)与丹尼斯里奇(Dennis Ritchie)一起开发了 Unix 操作系统。Unix 是用汇编语言写的,无法移植到其他计算机&…...
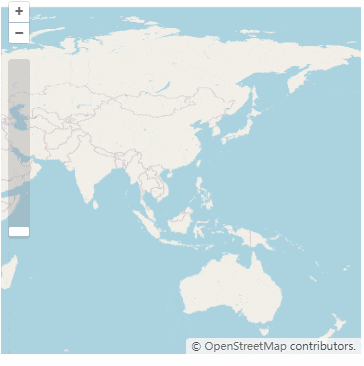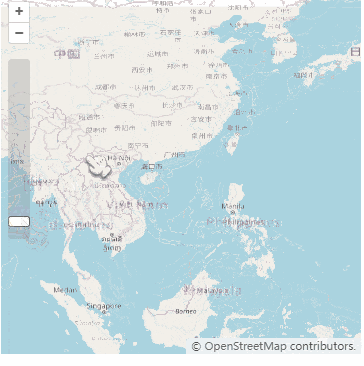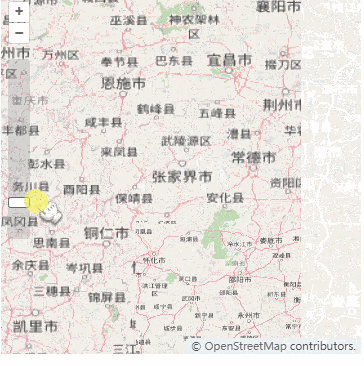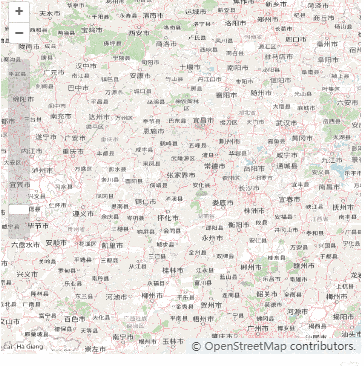
OpenLayers.js 入门教程:打造互动地图的入门指南
本文简介 戴尬猴,我是德育处主任 本文介绍如何使用 OpenLayers.js (后面简称 ol)。ol 是一个开源 JavaScript 库,可用于在Web页面上创建交互式地图。 ol能帮助我们在浏览器轻松地使用地图功能,例如地图缩放、地图拖动…...
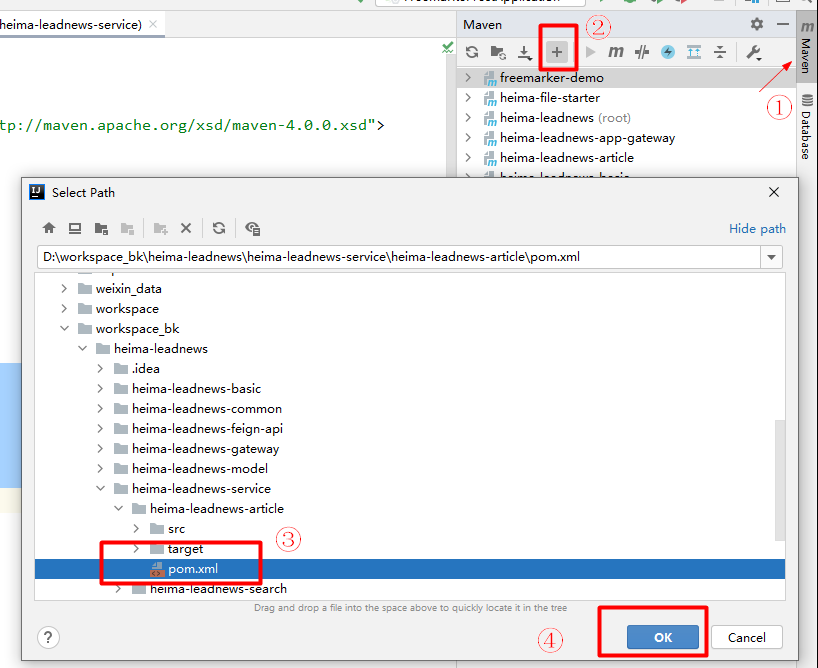
黑马头条:app端文章查看
黑马头条:app端文章查看 黑马头条:app端文章查看文章列表加载1. 需求分析2. 表结构分析3. 导入文章数据库3.1 导入数据库3.2 导入对应的实体类 4. 实现思路5. 接口定义6. 功能实现6.1:导入heima-leadnews-article微服务,资料在当天…...
)
常见使用总结篇(一)
Autowired和Resource注解的区别 Autowired注解是Spring提供的,Resource注解是J2EE本身提供Autowird注解默认通过byType方式注入(没有匹配会通过byName方式),而Resource注解默认通过byName方式注入(没有匹配会通过byType方式)Autowired注解注入的对象需要…...

【软考系统架构设计师】2023年系统架构师冲刺模拟习题之《数据库系统》
在数据库章节中可能会考察以下内容: 文章目录 数据库完整性约束🌟数据库模式🌟🌟ER模式🌟关系代数🌟🌟并发控制🌟数据仓库与数据挖掘🌟🌟反规范化技术&#x…...
北邮22级信通院数电:Verilog-FPGA(7)第七周实验(1):带使能端的38译码器全加器(关注我的uu们加群咯~)
北邮22信通一枚~ 跟随课程进度更新北邮信通院数字系统设计的笔记、代码和文章 持续关注作者 迎接数电实验学习~ 获取更多文章,请访问专栏: 北邮22级信通院数电实验_青山如墨雨如画的博客-CSDN博客 关注作者的uu们可以进群啦~ 目录 方法一ÿ…...

SIT3491ISO具有隔离功能,256 节点,全双工 RS422/RS485 芯片
SIT3491ISO 是一款电容隔离的全双工 RS-422/485 收发器,总线端口 ESD 保护能力 HBM 达到 15kV 以上,功能完全满足 EIA-422 以及 TIA/EIA-485 标准要求的 RS-422/485 收发器。 SIT3491ISO 包括一个驱动器和一个接收器,两者均…...
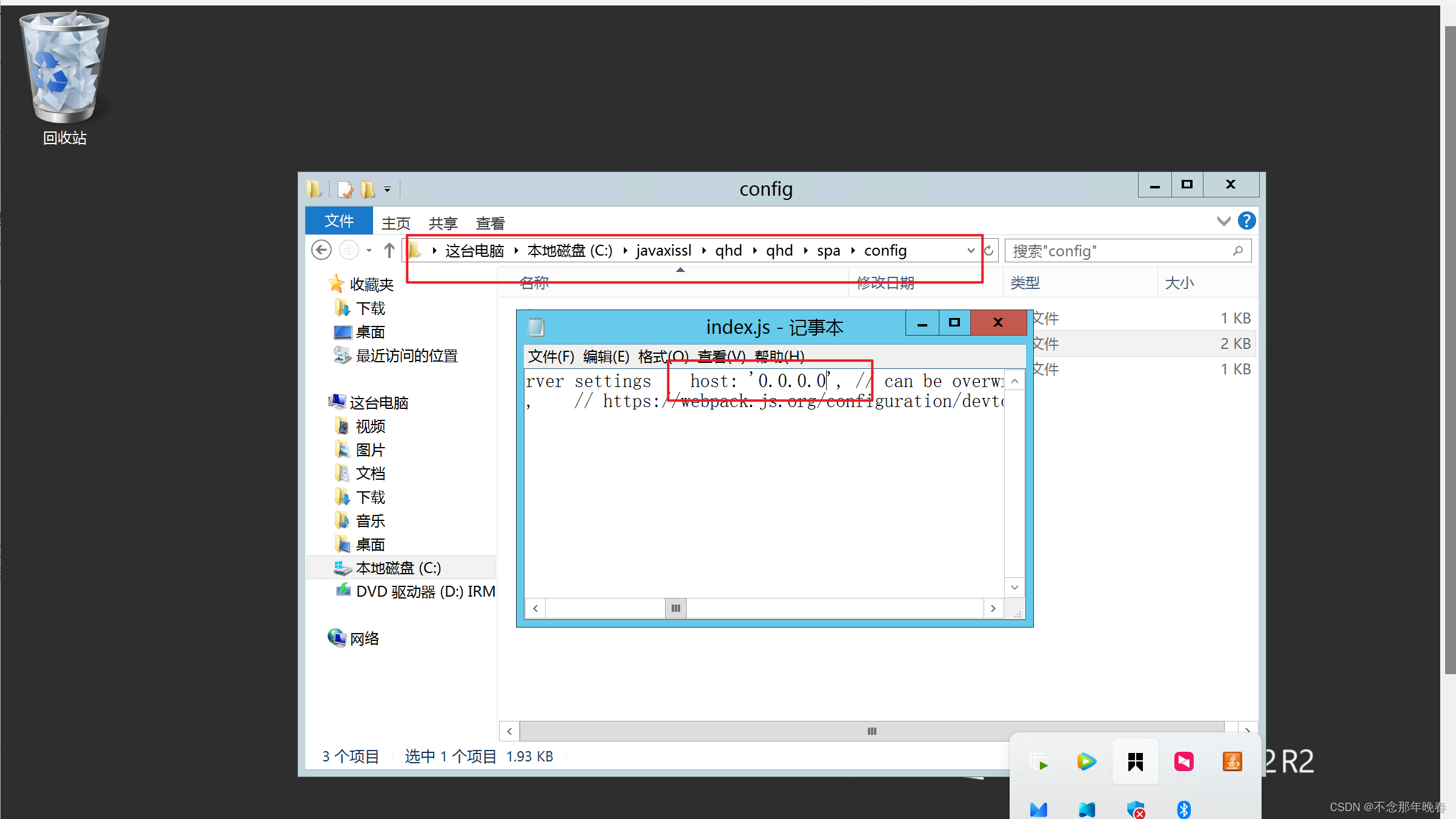
在windows服务器上部署一个单机项目以及前后端分离项目
目录 一. 单机项目在windows服务器上的部署 1.1 在本机上测试项目无误 1.1.1 在数据库中测试sql文件没问题 1.1.2 在tomcat中测试war文件无误 1.1.3 测试完成后,进入浏览器运行单机项目确保无误 1.2 在windows服务器中运行项目 二. 前后端分离项目在服务器上…...
)
使用jdbc技术,在数据库中存储大数据对象(使用字节IO流读取图片等给blob等二进制类型数据赋值)
在MySQL中,BLOB是一种数据类型,代表二进制大对象(Binary Large Object),可以存储大量的二进制数据,如图像、声音、视频等。BLOB类型的数据在存储和检索时会以二进制方式进行处理,而不是字符方式…...
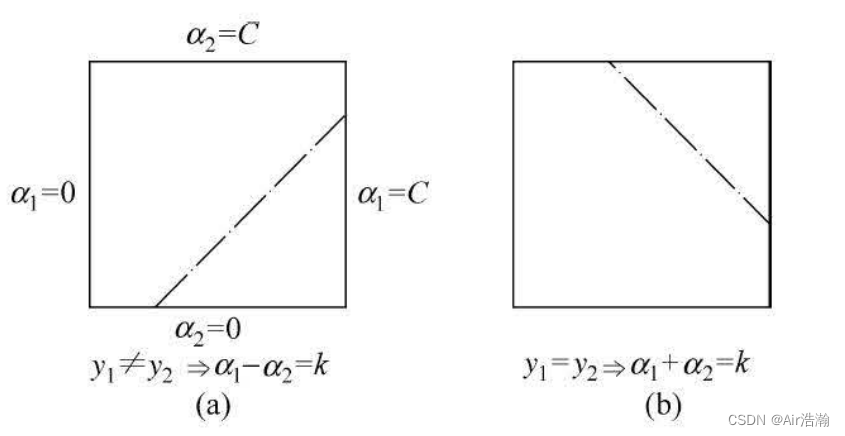
统计学习方法 支持向量机(下)
文章目录 统计学习方法 支持向量机(下)非线性支持向量机与和核函数核技巧正定核常用核函数非线性 SVM 序列最小最优化算法两个变量二次规划的求解方法变量的选择方法SMO 算法 统计学习方法 支持向量机(下) 学习李航的《统计学习方…...

【python】如何注释
一:通过#注释行 #这个是个注释 print(hello world) 二:通过或"""注释段落 这个注释段落 这是注释段落 这是注释段落print(hello world) """ 这是多行注释,用三个双引号 这是多行注释,用三个双引…...
C++——C++入门(二)
C 前言一、引用引用概念引用特性常引用使用场景传值、传引用效率比较值和引用的作为返回值类型的性能比较 引用和指针的区别 二、内联函数概念特性知识点提升 三、auto关键字类型别名思考auto简介auto的使用细则auto不能推导的场景 四、基于范围的for循环范围for的语法范围for的…...
容联七陌百度营销通BCP解决方案,让营销更精准
百度营销通作为一个快速迭代、满足客户多元化营销需求的高效率营销工具成为众多企业的选择,通过百度营销通BCP对接,企业就可以在百度咨询页接入会话,收集百度来源的访客搜索关键词,通过百度推广获取更多的精准客户,从而…...

Transformer模型 | 用于目标检测的视觉Transformers训练策略
基于视觉的Transformer在预测准确的3D边界盒方面在自动驾驶感知模块中显示出巨大的应用,因为它具有强大的建模视觉特征之间远程依赖关系的能力。然而,最初为语言模型设计的变形金刚主要关注的是性能准确性,而不是推理时间预算。对于像自动驾驶这样的安全关键系统,车载计算机…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...

elementUI点击浏览table所选行数据查看文档
项目场景: table按照要求特定的数据变成按钮可以点击 解决方案: <el-table-columnprop"mlname"label"名称"align"center"width"180"><template slot-scope"scope"><el-buttonv-if&qu…...

AI语音助手的Python实现
引言 语音助手(如小爱同学、Siri)通过语音识别、自然语言处理(NLP)和语音合成技术,为用户提供直观、高效的交互体验。随着人工智能的普及,Python开发者可以利用开源库和AI模型,快速构建自定义语音助手。本文由浅入深,详细介绍如何使用Python开发AI语音助手,涵盖基础功…...

Unity VR/MR开发-VR开发与传统3D开发的差异
视频讲解链接:【XR马斯维】VR/MR开发与传统3D开发的差异【UnityVR/MR开发教程--入门】_哔哩哔哩_bilibili...
