8类放球问题
放球问题简介
放球问题是一类很有意思的排列组合问题。通俗来说,就是把n个小球放到m个盒子里,问有几种放法。根据小球是否相同,盒子是否相同,是否允许有空盒,又可以把问题细分为8个具体的问题。其中有一些问题是非常简单的,有一些问题经常出现在一些经典的排列组合问题当中,有一些问题则比较有难度,难以通过一个表达式直接写出答案。
放球问题的解法
我们分8种情况具体讨论这个问题。假设有n个小球,m个盒子,且默认n ≥ \geq ≥m。我们就从易到难,慢慢来分析。
1.球不同,盒不同,允许有空盒
这是最简单的一种情况。对于每个小球,有m种放法,一共有n个小球,于是一共有 m n m^n mn种放法。
2.球相同,盒不同,不允许有空盒
由于球相同,我们可以把每个球看成一个0,n个球组成了一个长度为n的全0序列。放小球的过程可以看成把这个序列分为m段,且每段长度大于0。于是我们就可以用隔板法解决了。问题相当于在这个长度为n的序列中插入m-1个隔板,从而就把序列分成了m段。这个序列有n-1个间隙,为了保证每段长度大于0,则只需要两块隔板不放在同一个间隙中。于是问题就变成了,在n-1个间隙中,挑选m-1个位置放隔板,即 C n − 1 m − 1 C_{n-1}^{m-1} Cn−1m−1种放法。
3.球相同,盒不同,允许有空盒
这个有两种做法。第一种做法是这样的。跟上面那种情况类似,也是看成一个序列,但是两个隔板是可以相邻的。n个球,m-1个隔板,一共长度为n+m-1。我们只需要在这个n+m-1个位置中选m-1个位置作为隔板即可,于是有 C n + m − 1 m − 1 C_{n+m-1}^{m-1} Cn+m−1m−1种放法。
第二种做法是,可以认为我们一开始有n+m个小球,先在每个盒中放上一个小球。于是问题就转化为了n+m个球放在m个盒子里,不允许有空盒的情况。套用上面的公式,得有 C n + m − 1 m − 1 C_{n+m-1}^{m-1} Cn+m−1m−1种放法。
4.球不同,盒不相同,不允许有空盒
到这里,问题开始变得难起来了。正难则反,我们反过来,考虑必定存在空盒的情况。这里我们采用容斥原理的方法做。由于盒子不同,给每个盒子从1-m编个号。令 A i A_i Ai表示第i个盒子是空的情况,|A|表示在A情况下的方案数。比如 ∣ A i ∣ |A_i| ∣Ai∣表示第i个盒子一定是空盒的方案数,那么 ∣ A i ∣ = ( m − 1 ) n |A_i|=(m-1)^n ∣Ai∣=(m−1)n。
∣ A i ∩ A j ∣ |A_i \cap A_j| ∣Ai∩Aj∣表示第i个盒子和第j个盒子同时是空盒的情况数,即 ( m − 2 ) n (m-2)^n (m−2)n种。我们要求有空盒的方案数,即 ∣ A 1 ∪ A 2 ∪ ⋯ ∪ A m ∣ |A_1\cup A_2\cup \cdots \cup A_m| ∣A1∪A2∪⋯∪Am∣。
根据容斥原理的公式,
∣ A 1 ∪ A 2 ∪ ⋯ ∪ A m ∣ = ∑ 1 ≤ i ≤ m ∣ A i ∣ − ∑ 1 ≤ i < j ≤ m ∣ A i ∩ A j ∣ + ∑ 1 ≤ i < j < k ≤ m ∣ A i ∩ A j ∩ A k ∣ − ⋯ + ( − 1 ) m − 1 ∣ A 1 ∩ A 2 ∩ ⋯ ∩ A m ∣ = C m 1 ( m − 1 ) n − C m 2 ( m − 2 ) n + C m 3 ( m − 3 ) n − ⋯ + ( − 1 ) m − 1 C m m ( m − m ) n = ∑ k = 1 m ( − 1 ) k − 1 C m k ( m − k ) n |A_1\cup A_2\cup \cdots \cup A_m|=\sum_{1\leq i \leq m}{|A_i|}-\sum_{1\leq i<j \leq m}{|A_i \cap A_j|}+\sum_{1 \leq i<j<k \leq m}{|A_i \cap A_j \cap A_k|}-\cdots+(-1)^{m-1}|A_1 \cap A_2 \cap \cdots \cap A_m|=C_m^1(m-1)^n-C_m^2(m-2)^n+C_m^3(m-3)^n-\cdots +(-1)^{m-1}C_m^m(m-m)^n=\sum_{k=1}^m{(-1)^{k-1}C_m^k(m-k)^n} ∣A1∪A2∪⋯∪Am∣=∑1≤i≤m∣Ai∣−∑1≤i<j≤m∣Ai∩Aj∣+∑1≤i<j<k≤m∣Ai∩Aj∩Ak∣−⋯+(−1)m−1∣A1∩A2∩⋯∩Am∣=Cm1(m−1)n−Cm2(m−2)n+Cm3(m−3)n−⋯+(−1)m−1Cmm(m−m)n=∑k=1m(−1)k−1Cmk(m−k)n
必定存在空盒的方案数有 ∑ k = 1 m ( − 1 ) k − 1 C m k ( m − k ) n \sum_{k=1}^m{(-1)^{k-1}C_m^k(m-k)^n} ∑k=1m(−1)k−1Cmk(m−k)n种,那么不存在空盒的方案数有 m n − ∑ k = 1 m ( − 1 ) k − 1 C m k ( m − k ) n = ∑ k = 0 m ( − 1 ) k C m k ( m − k ) n m^n-\sum_{k=1}^m{(-1)^{k-1}C_m^k(m-k)^n}=\sum_{k=0}^m{(-1)^kC_m^k(m-k)^n} mn−∑k=1m(−1)k−1Cmk(m−k)n=∑k=0m(−1)kCmk(m−k)n
总的来说,求解的思路是通过容斥原理,把较难的不允许有空盒的情况转化为较为容易的允许有空盒的情况。
5.球不同,盒相同,不允许有空盒
这个问题跟上一个问题相比,仅仅是盒不同改成了盒相同,那么由于球不同,所以这个问题的放法是上面问题放法的 1 m ! \frac{1}{m!} m!1,即 1 m ! ∑ k = 0 m ( − 1 ) k C m k ( m − k ) n \frac{1}{m!}\sum_{k=0}^m{(-1)^kC_m^k(m-k)^n} m!1∑k=0m(−1)kCmk(m−k)n
由于该问题求解起来较为复杂,所以人们为这个问题专门定义了一个术语——第二类斯特林数。第二类斯特林数 S ( n , m ) S(n,m) S(n,m)表示将n个不同的小球放在m个相同的盒子中,不允许有空盒的方案数。
那么,根据我们的推导, S ( n , m ) = 1 m ! ∑ k = 0 m ( − 1 ) k C m k ( m − k ) n S(n,m)=\frac{1}{m!}\sum_{k=0}^m{(-1)^kC_m^k(m-k)^n} S(n,m)=m!1∑k=0m(−1)kCmk(m−k)n。
同时,这也是 S ( n , m ) S(n,m) S(n,m)的通项公式。
6.球不同,盒相同,允许有空盒
相比于上面的问题,这个问题允许有空盒了。那么我们只需要枚举非空盒的个数,就能转化为上面的问题了。有i个非空盒时,方案数为 S ( n , i ) S(n,i) S(n,i)。于是总方案数为 ∑ i = 1 m S ( n , i ) \sum_{i=1}^m{S(n,i)} ∑i=1mS(n,i)
7.球相同,盒相同,允许有空盒
这个问题可以用母函数的方法做,但是由于本人才疏学浅,没有学过母函数的方法,于是在这里提供一种递推的解法。
设方案数为 f ( n , m ) f(n,m) f(n,m)。
先给出边界情况,当小球数为0或盒子数为1,肯定就只有1种方案了。
再分类讨论,给出递推关系式。
若小球数比盒子数少,则多出来的盒子只能空着,于是有 f ( n , m ) = f ( n , n ) , n < m f(n,m)=f(n,n),n<m f(n,m)=f(n,n),n<m
若小球数不比盒子数少,那么我们就要放小球了。整体思路是,把盒子排成一排,后面的盒子放的小球数不能超过前面盒子的小球数。这样枚举的话,才能不重不漏。我们考虑当前的最后一个盒子,有放小球和不放小球两种情况。如果空着,方案数为 f ( n , m − 1 ) f(n,m-1) f(n,m−1)。如果要放小球,由于这个盒子的小球必须是最少的,所以前面所有盒子都要放一个小球,这样的方案数为 f ( n − m , m ) f(n-m,m) f(n−m,m)。
合起来,可以得到 f ( n , m ) f(n,m) f(n,m)的递推表达式
f ( n , m ) = { 1 n = 0 ∣ ∣ m = 1 f ( n , n ) n < m f ( n − m , m ) + f ( n , m − 1 ) n ≥ m f(n,m)=\begin{cases} 1 & n=0 || m=1 \\ f(n,n) & n<m \\ f(n-m,m)+f(n,m-1) & n\geq m \end{cases} f(n,m)=⎩ ⎨ ⎧1f(n,n)f(n−m,m)+f(n,m−1)n=0∣∣m=1n<mn≥m
8.球相同,盒相同,不允许有空盒
既然球跟盒都相同,那不妨拿出m个球,先在每个盒子里放上一个球。这样问题就转化为,将n-m个相同的小球放到m个盒子里,允许有空盒的问题了。方案数即为 f ( n − m , m ) f(n-m,m) f(n−m,m)
代码
下面是我写的python代码
import math
def f(n,m):if n==0 or m==1:return 1if n<m:return f(n,n)return f(n-m,m)+f(n,m-1)
def S(n,m):return sum((-1)**k * math.comb(m, k) * math.pow(m-k, n) for k in range(m+1))/math.factorial(m)
def fangqiu(n,m,qiu,he,kong): #n表示球数,m表示盒数,qiu表示小球是否相同,he表示盒子是否相同,kong表示是否允许有空盒if qiu==0 and he==0 and kong==1:return m**nif qiu==1 and he==0 and kong==0:return math.comb(n-1,m-1)if qiu==1 and he==0 and kong==1:return math.comb(n+m-1,m-1)if qiu==0 and he==0 and kong==0:return S(n, m)*math.factorial(m)if qiu==0 and he==1 and kong==0:return S(n, m)if qiu==0 and he==1 and kong==1:return sum(S(n,i) for i in range(1,m+1))if qiu==1 and he==1 and kong==1:return f(n,m)if qiu==1 and he==1 and kong==0:return f(n-m,m)
n,m=map(int,input().split())
print(int(fangqiu(n,m,0,0,1)))
总结
虽然我们按一定的标准,划分出了8个问题,但其实这8个问题又有很多变种。比如,我们只关注了 n ≥ m n\geq m n≥m的情况,我们得出的结论一部分对 n ≤ m n\leq m n≤m适用,一部分却不适用了。掌握解决这一类问题的方法比记住结论更加重要。
相关文章:

8类放球问题
放球问题简介 放球问题是一类很有意思的排列组合问题。通俗来说,就是把n个小球放到m个盒子里,问有几种放法。根据小球是否相同,盒子是否相同,是否允许有空盒,又可以把问题细分为8个具体的问题。其中有一些问题是非常简…...

【APP VTable】和市面上的 Table 组件一样,都是接收表格[] 以及数据源[]
博主:_LJaXi Or 東方幻想郷 专栏: uni-app | 小程序开发 开发工具:HBuilderX 这里写目录标题 表格组件USE 表格组件 <template><view class"scroll-table-wrapper"><view class"scroll-table-container"…...

深度学习 anaconda 安装问题
配置anaconda 在官网下载匹配版本的anaconda(官网下载可能时间比较长),可以选择清华镜像。 安装过程默认即可,或者根据情况进行修改。 旧版本是可以在安装的时候勾选添加路径到环境变量中的,但是我安装的是2023.9月…...
为什么现在学Rust编程是最好时机?
1.摘要 Rust是由Mozilla主导开发的通用、编译型编程语言。设计准则为:安全、并发、实用,支持函数式、并发式、过程式以及面向对象的编程风格。Rust的设计目标之一,是要使设计大型的互联网客户端和服务器的任务变得更容易,因此更加强调安全性、存储器配置以及并发处理等方面的特…...
Java——Spring的控制反转(一文详解IOC)
Spring,Spring MVC,Spring Boot 三者比较 答: 这三者专注的领域不同,解决的问题也不一样;总的来说,Spring 就像一个大家族,有众多衍生产品例如 Boot,Security,JPA等等。…...
Android Glide限定onlyRetrieveFromCache取内存缓存submit超时阻塞方式,Kotlin
Android Glide限定onlyRetrieveFromCache取内存缓存submit超时阻塞方式,Kotlin import android.os.Bundle import android.util.Log import android.widget.ImageView import androidx.appcompat.app.AppCompatActivity import androidx.lifecycle.lifecycleScope import com.b…...
tinymce输入框怎么限制只输入空格或者回车时不能提交
项目场景: 项目相关背景: tinymce输入框只输入空格或者回车时提交的空数据毫无意义,所以需要限制一下 无意义的输入: 解决方案: 因为tinymce输入框传到后端的数据是代码形式,所以不能直接.trem&#…...
时间、空间复杂度的例题详解
文章前言 上篇文章带大家认识了数据结构和算法的含义,以及理解了时间、空间复杂度,那么接下来来深入理解一下时间、空间复杂度。 时间复杂度实例 实例1 // 计算Func2的时间复杂度? void Func2(int N) {int count 0;for (int k 0; k <…...

Ubuntu22.04 搭建 OpenHarmony 命令行开发环境
文章目录 简介安装工具链获取gitee源码安装编译工具编译测试 简介 在本文中,我们将介绍如何使用命令行工具在你的设备上安装OpenHarmony操作系统。OpenHarmony是一个开源的、面向物联网(IoT)设备的操作系统,它提供了一套全面的开…...
)
10.27 知识总结(前端)
一、 前端 1.1 什么是前端? 前端是所有跟用户直接打交道的都可以称之为是前端 比如:PC页面、手机页面、平板页面、汽车显示屏、大屏幕展示出来的都是前端内容 通俗点就是能够用肉眼看到的都是“前端” 1.2 为什么要学前端 学了前端以后我们就可以做全栈工…...

操作系统(02326)考试题库
博客主页:https://tomcat.blog.csdn.net 博主昵称:农民工老王 主要领域:Java、Linux、K8S 期待大家的关注💖点赞👍收藏⭐留言💬 目录 单选题多选题主观题 单选题 把并发进程中与共享变量有关的程序段称为…...
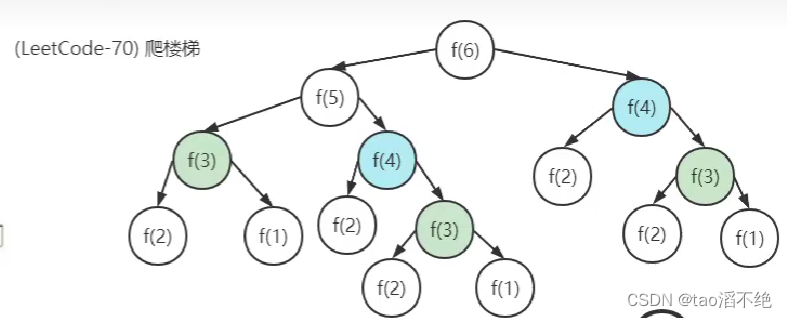
LeetCode题:70爬楼梯,126斐波那契数
目录 70:爬楼梯 题目要求: 解题思路:(类似斐波那契数) 递归解法: 非递归解法: 126:斐波那契数 题目要求: 解题思路: 递归解法: 非递归解…...
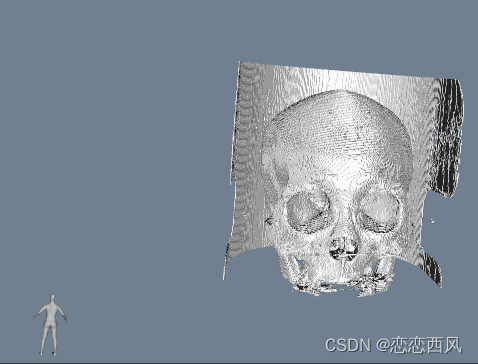
VTK OrientationMarker 方向 三维坐标系 相机坐标轴 自定义坐标轴
本文 以 Python 语言开发 我们在做三维软件开发时,经常会用到相机坐标轴,来指示当前空间位置; 坐标轴效果: 相机方向坐标轴 Cube 正方体坐标轴 自定义坐标轴: Code: Axes def main():colors vtkNamedC…...

工控安全与网络安全有什么不同?
在当代,全球制造业正在经历一场前所未有的技术变革。工业4.0不仅代表着自动化和数据交换的进步,它还揭示了工业自动化、智能制造与系统集成的融合。这种集成为企业带来了效率和质量的双重提升,但同时也暴露出新的安全隐患。工控系统成为了这一…...

性能测试工具:Jmeter介绍
JMeter是一个开源的Java应用程序,由Apache软件基金会开发和维护,可用于性能测试、压力测试、接口测试等。 1. 原理 JMeter的基本原理是模拟多用户并发访问应用程序,通过发送HTTP请求或其他协议请求,并测量响应时间、吞吐量、并发…...

Golang Struct 继承的深入讨论和细节
1)结构体可以使用嵌套匿名结构体所有的字段和方法,即:首字母大写或者小写的字段、方法,都可以使用。 type A struct {Name stringage int }func (a *A) SayName() {fmt.Println("A say name", a.Name) }func (a *A) s…...

Android11分区介绍
1.分区汇总 3566及3568分区对应如下: rockdev/Image-rk3566_rgo/ ├── boot.img ├── dtbo.img ├── MiniLoaderAll.bin ├── misc.img ├── parameter.txt ├── recovery.img ├── super.img ├── uboot.img └── vbmeta.img 2.分区说明 分区 说明 boo…...

goland无法调试问题解决
goland 无法调试问题解决 golang 版本升级后,goland 无法进行调试了 首先请看自己下载的版本是否有误 1.apple系 M系列芯片的 arm64版本 2.apple系 intel系列芯片的x86_64 3.windows系 intel解决如下: 查看gopath ericsanchezErics-Mac-mini gww-api…...

关于近期IP-Guard新版本客户端重复发送邮件的问题处理说明
关于近期新版本客户端重复发送邮件的问题处理说明 一、问题描述 近期部分客户反馈,升级到新版本的客户端(4.81.341.0、4.82.621.0及以上),使用SMTP协议发送邮件时,会出现重复发送邮件的情况,主要表现为以下两种现象: Outlook发送包含大量收件人的邮件时,收件人邮箱可能…...

linux java 启动脚本
#!/bin/sh## java env #export JAVA_HOME/data/jdk1.8.0_121 #export JRE_HOME$JAVA_HOME/jre## service name #当前目录 SERVICE_DIR$(cd dirname $0; pwd) echo "$SERVICE_DIR" #jar包路径 JAR_DIRls -ltr $SERVICE_DIR/*.jar| tail -1 echo "JAR_DIR $JAR_DI…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

mac 安装homebrew (nvm 及git)
mac 安装nvm 及git 万恶之源 mac 安装这些东西离不开Xcode。及homebrew 一、先说安装git步骤 通用: 方法一:使用 Homebrew 安装 Git(推荐) 步骤如下:打开终端(Terminal.app) 1.安装 Homebrew…...

NPOI Excel用OLE对象的形式插入文件附件以及插入图片
static void Main(string[] args) {XlsWithObjData();Console.WriteLine("输出完成"); }static void XlsWithObjData() {// 创建工作簿和单元格,只有HSSFWorkbook,XSSFWorkbook不可以HSSFWorkbook workbook new HSSFWorkbook();HSSFSheet sheet (HSSFSheet)workboo…...

BLEU评分:机器翻译质量评估的黄金标准
BLEU评分:机器翻译质量评估的黄金标准 1. 引言 在自然语言处理(NLP)领域,衡量一个机器翻译模型的性能至关重要。BLEU (Bilingual Evaluation Understudy) 作为一种自动化评估指标,自2002年由IBM的Kishore Papineni等人提出以来,…...

通过 Ansible 在 Windows 2022 上安装 IIS Web 服务器
拓扑结构 这是一个用于通过 Ansible 部署 IIS Web 服务器的实验室拓扑。 前提条件: 在被管理的节点上安装WinRm 准备一张自签名的证书 开放防火墙入站tcp 5985 5986端口 准备自签名证书 PS C:\Users\azureuser> $cert New-SelfSignedCertificate -DnsName &…...

CVPR2025重磅突破:AnomalyAny框架实现单样本生成逼真异常数据,破解视觉检测瓶颈!
本文介绍了一种名为AnomalyAny的创新框架,该方法利用Stable Diffusion的强大生成能力,仅需单个正常样本和文本描述,即可生成逼真且多样化的异常样本,有效解决了视觉异常检测中异常样本稀缺的难题,为工业质检、医疗影像…...
