基于大数据的时间序列股价预测分析与可视化 - lstm 计算机竞赛
文章目录
- 1 前言
- 2 时间序列的由来
- 2.1 四种模型的名称:
- 3 数据预览
- 4 理论公式
- 4.1 协方差
- 4.2 相关系数
- 4.3 scikit-learn计算相关性
- 5 金融数据的时序分析
- 5.1 数据概况
- 5.2 序列变化情况计算
- 最后
1 前言
🔥 优质竞赛项目系列,今天要分享的是
🚩 毕业设计 大数据时间序列股价预测分析系统
该项目较为新颖,适合作为竞赛课题方向,学长非常推荐!
🥇学长这里给一个题目综合评分(每项满分5分)
- 难度系数:3分
- 工作量:3分
- 创新点:3分
🧿 更多资料, 项目分享:
https://gitee.com/dancheng-senior/postgraduate
2 时间序列的由来
提到时间序列分析技术,就不得不说到其中的AR/MA/ARMA/ARIMA分析模型。这四种分析方法的共同特点都是跳出变动成分的分析角度,从时间序列本身出发,力求得出前期数据与后期数据的量化关系,从而建立前期数据为自变量,后期数据为因变量的模型,达到预测的目的。来个通俗的比喻,大前天的你、前天的你、昨天的你造就了今天的你。
2.1 四种模型的名称:
- AR模型:自回归模型(Auto Regressive model);
- MA模型:移动平均模型(Moving Average model);
- ARMA:自回归移动平均模型(Auto Regressive and Moving Average model);
- ARIMA模型:差分自回归移动平均模型。
- AR模型:
如果某个时间序列的任意数值可以表示成下面的回归方程,那么该时间序列服从p阶的自回归过程,可以表示为AR§:

AR模型利用前期数值与后期数值的相关关系(自相关),建立包含前期数值和后期数值的回归方程,达到预测的目的,因此成为自回归过程。这里需要解释白噪声,白噪声可以理解成时间序列数值的随机波动,这些随机波动的总和会等于0,例如,某饼干自动化生产线,要求每包饼干为500克,但是生产出来的饼干产品由于随机因素的影响,不可能精确的等于500克,而是会在500克上下波动,这些波动的总和将会等于互相抵消等于0。
3 数据预览
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
#准备两个数组
list1 = [6,4,8]
list2 = [8,6,10]#分别将list1,list2转为Series数组
list1_series = pd.Series(list1)
print(list1_series)
list2_series = pd.Series(list2)
print(list2_series)#将两个Series转为DataFrame,对应列名分别为A和B
frame = { 'Col A': list1_series, 'Col B': list2_series }
result = pd.DataFrame(frame)result.plot()
plt.show()
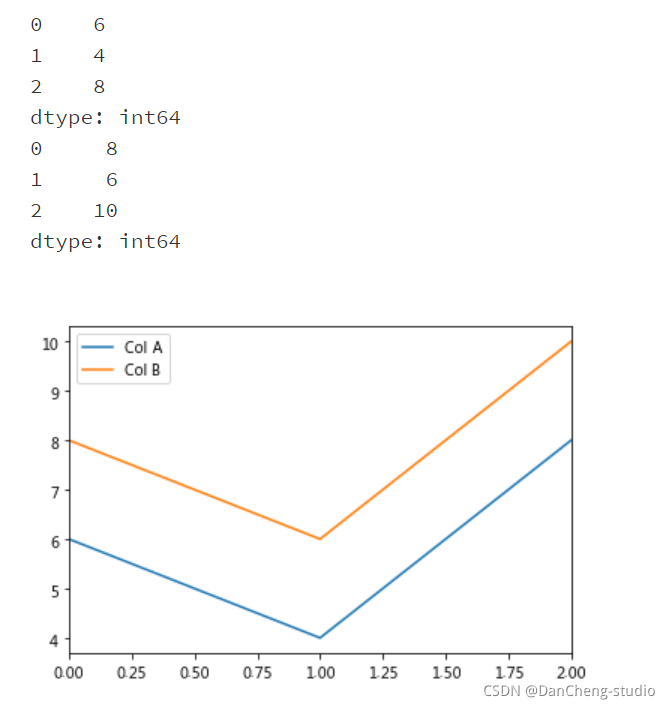
4 理论公式
4.1 协方差
首先看下协方差的公式:
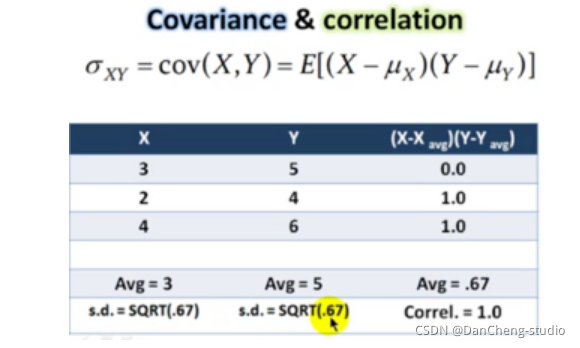
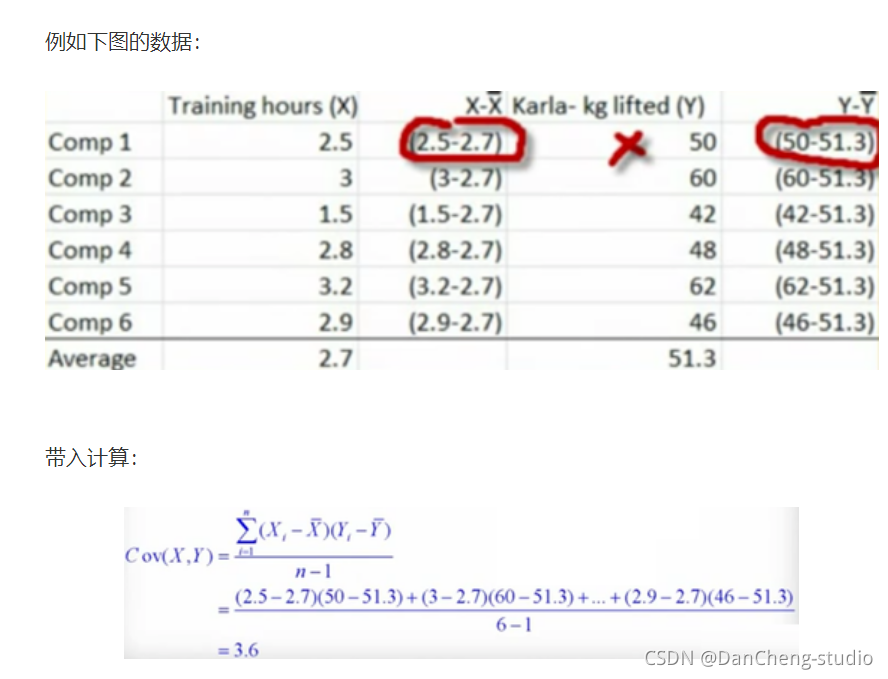
4.2 相关系数
计算出Cov后,就可以计算相关系数了,值在-1到1之间,越接近1,说明正相关性越大;越接近-1,则负相关性越大,0为无相关性
公式如下:
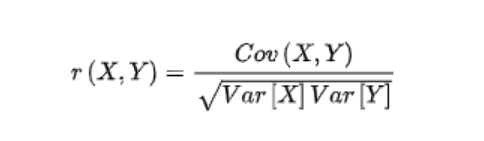
4.3 scikit-learn计算相关性
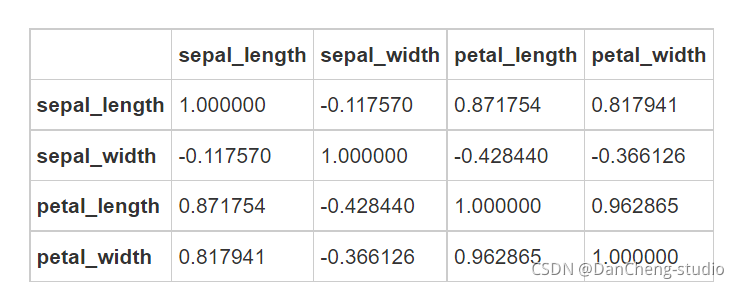
#各特征间关系的矩阵图
sns.pairplot(iris, hue=‘species’, size=3, aspect=1)
Andrews Curves 是一种通过将每个观察映射到函数来可视化多维数据的方法。
使用 Andrews Curves 将每个多变量观测值转换为曲线并表示傅立叶级数的系数,这对于检测时间序列数据中的异常值很有用。
plt.subplots(figsize = (10,8))
pd.plotting.andrews_curves(iris, ‘species’, colormap=‘cool’)

这里以经典的鸢尾花数据集为例
setosa、versicolor、virginica代表了三个品种的鸢尾花。可以看出各个特征间有交集,也有一定的分别规律。
#最后,通过热图找出数据集中不同特征之间的相关性,高正值或负值表明特征具有高度相关性:
fig=plt.gcf()
fig.set_size_inches(10,6)
fig=sns.heatmap(iris.corr(), annot=True, cmap='GnBu', linewidths=1, linecolor='k', \
square=True, mask=False, vmin=-1, vmax=1, \
cbar_kws={"orientation": "vertical"}, cbar=True)

5 金融数据的时序分析
主要介绍:时间序列变化情况计算、时间序列重采样以及窗口函数
5.1 数据概况
import pandas as pd
tm = pd.read_csv('/home/kesci/input/gupiao_us9955/Close.csv')
tm.head()
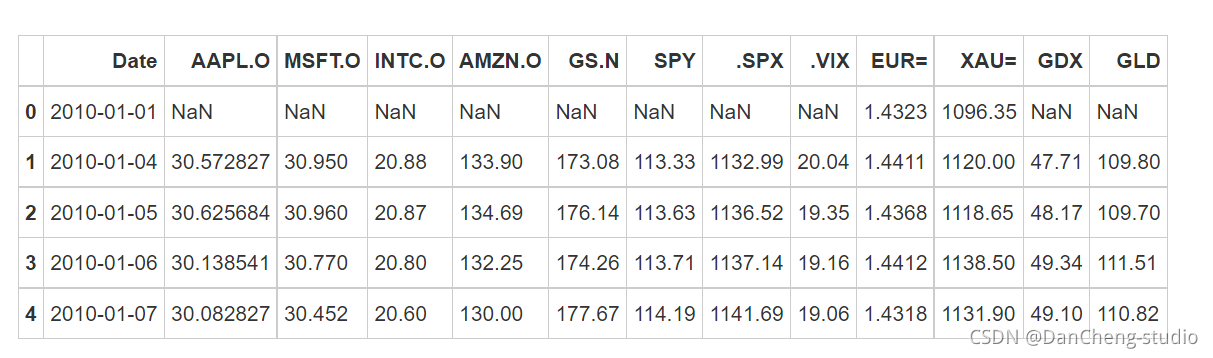
数据中各个指标含义:
- AAPL.O | Apple Stock
- MSFT.O | Microsoft Stock
- INTC.O | Intel Stock
- AMZN.O | Amazon Stock
- GS.N | Goldman Sachs Stock
- SPY | SPDR S&P; 500 ETF Trust
- .SPX | S&P; 500 Index
- .VIX | VIX Volatility Index
- EUR= | EUR/USD Exchange Rate
- XAU= | Gold Price
- GDX | VanEck Vectors Gold Miners ETF
- GLD | SPDR Gold Trust
8年期间价格(或指标)走势一览图
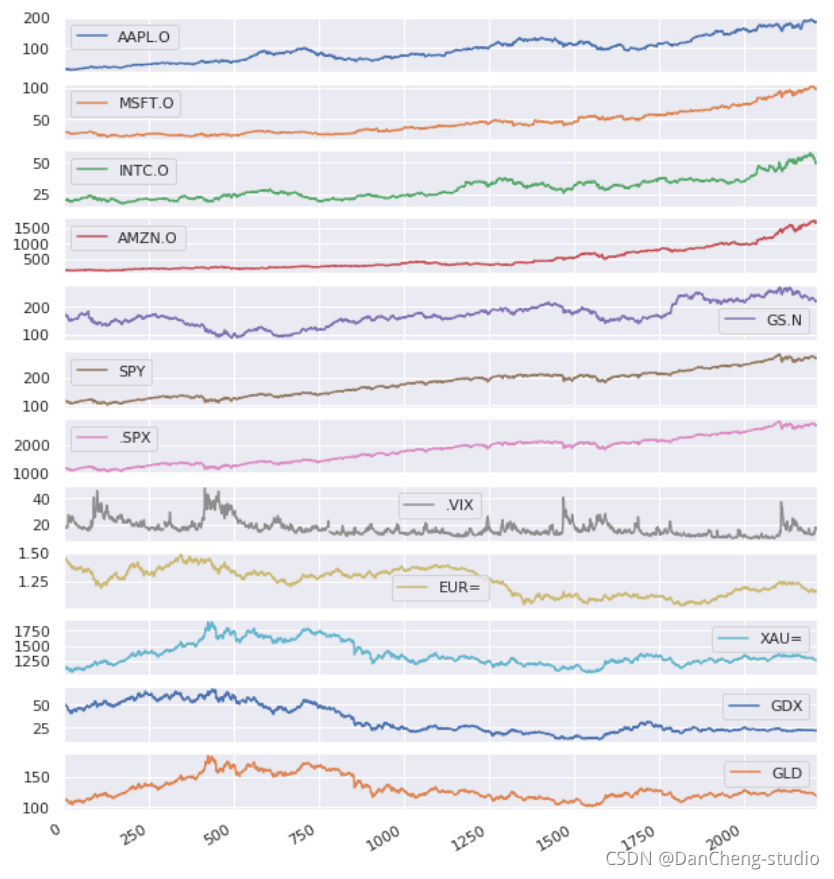
5.2 序列变化情况计算
- 计算每一天各项指标的差异值(后一天减去前一天结果)
- 计算pct_change:增长率也就是 (后一个值-前一个值)/前一个值)
- 计算平均计算pct_change指标
- 绘图观察哪个指标平均增长率最高
- 计算连续时间的增长率(其中需要计算今天价格和昨天价格的差异)
计算每一天各项指标的差异值(后一天减去前一天结果)
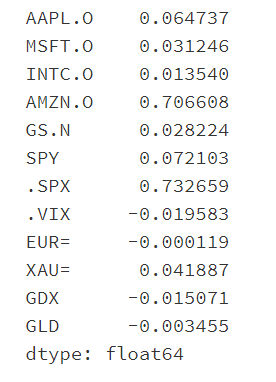
计算pct_change:增长率也就是 (后一个值-前一个值)/前一个值)
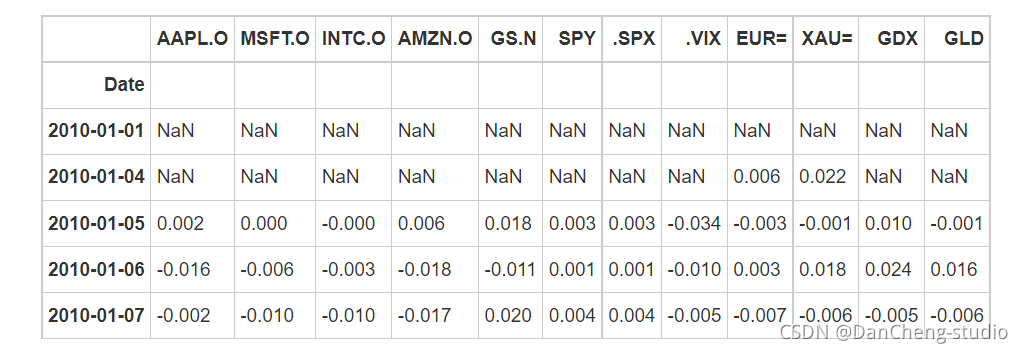
计算平均计算pct_change指标
绘图观察哪个指标平均增长率最高
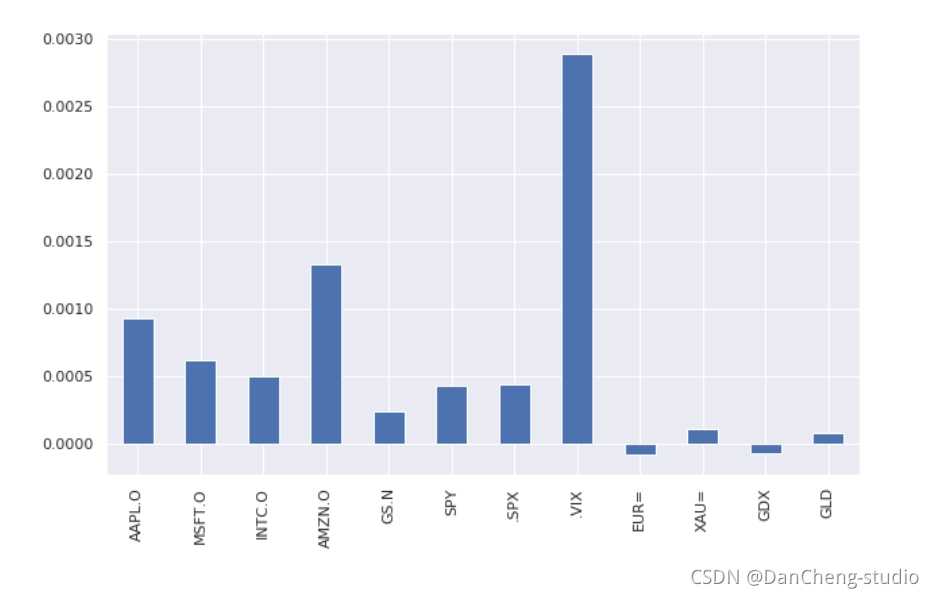
除了波动率指数(.VIX指标)增长率最高外,就是亚马逊的股价了!贝佐斯简直就是宇宙最强光头强
计算连续时间的增长率(其中需要计算今天价格和昨天价格的差异)
#第二天数据
tm.shift(1).head()
#计算增长率
rets = np.log(tm/tm.shift(1))
print(rets.tail().round(3))#cumsum的小栗子:
print('小栗子的结果:',np.cumsum([1,2,3,4]))#增长率做cumsum需要对log进行还原,用e^x
rets.cumsum().apply(np.exp).plot(figsize=(10,6))
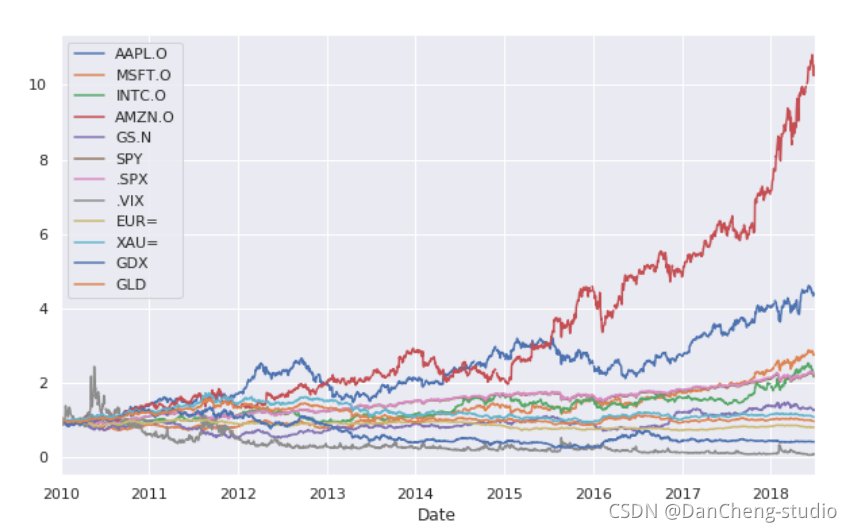
以上是在连续时间内的增长率,也就是说,2010年的1块钱,到2018年已经变为10多块了(以亚马逊为例)
(未完待续,该项目为demo预测部分有同学需要联系学长完成)
最后
🧿 更多资料, 项目分享:
https://gitee.com/dancheng-senior/postgraduate
相关文章:

基于大数据的时间序列股价预测分析与可视化 - lstm 计算机竞赛
文章目录 1 前言2 时间序列的由来2.1 四种模型的名称: 3 数据预览4 理论公式4.1 协方差4.2 相关系数4.3 scikit-learn计算相关性 5 金融数据的时序分析5.1 数据概况5.2 序列变化情况计算 最后 1 前言 🔥 优质竞赛项目系列,今天要分享的是 &…...
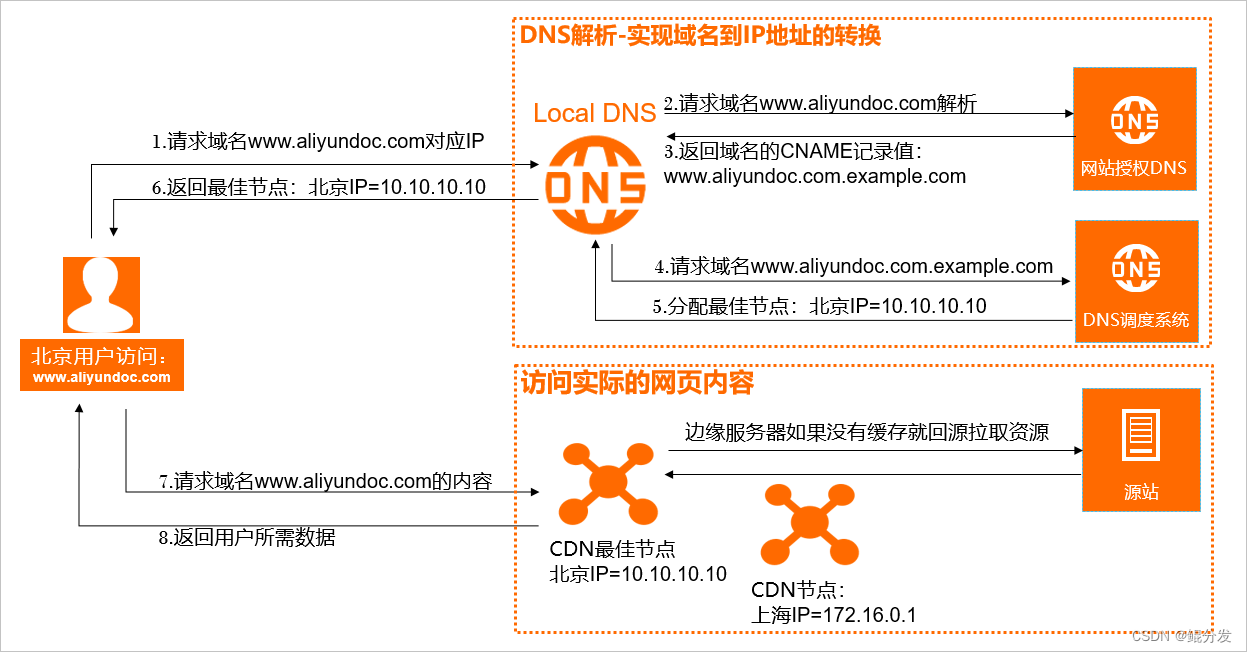
APP分发-CDN加速原理
摘要 CDN的全称是(Content Delivery Network),即内容分发网络。其目的是通过在现有的Internet中增加一层新的CACHE(缓存)层,将网站的内容发布到最接近用户的网络”边缘“的节点,使用户可以就近取得所需的内容,提高用户访问网站的…...

【Java 进阶篇】Java Request 继承体系详解
在Java编程中,Request(请求)是一个常见的概念,特别是在Web开发中。Request通常用于获取来自客户端的信息,以便服务器能够根据客户端的需求提供相应的响应。在Java中,Request通常涉及到一系列类和接口&#…...
通过阿里云创建accessKeyId和accessKeySecret
我们想实现服务端向个人发送短信验证码 需要通过accessKeyId和accessKeySecret 这里可以白嫖阿里云的 这里 我们先访问阿里云官网 阿里云地址 进入后搜索并进入短信服务 如果没登录 就 登录一下先 然后在搜索框搜索短信服务 点击进入 因为我也是第一次操作 我们一起点免费开…...

decapoda-research/llama-7b-hf 的踩坑记录
使用transformers加载decapoda-research/llama-7b-hf的踩坑记录。 ValueError: Tokenizer class LLaMATokenizer does not exist or is not currently imported. 解决办法: https://github.com/huggingface/transformers/issues/22222 将tokenizer_config.json中LLa…...

计算机操作系统重点概念整理-第六章 输入输出I/O管理【期末复习|考研复习】
第六章 输入输出I/O管理【期末复习|考研复习】 计算机操作系统系列文章传送门: 第一章 计算机系统概述 第二章 进程管理 第三章 进程同步 第四章 内存管理 第五章 文件管理 第六章 输出输出I/O管理 文章目录 第六章 输入输出I/O管理【期末复习|考研复习】前言六、输…...

uniapp开发小程序—picker结合后台数据实现二级联动的选择
一、效果图 二、完整代码 <template><view><picker mode"multiSelector" change"bindMultiPickerChange" columnchange"bindMultiPickerColumnChange":value"multiIndex" :range"multiArray"><view c…...
3D聚焦特效,自定义导航按钮等)
React Swiper.js使用(详细版)3D聚焦特效,自定义导航按钮等
共用代码 import swiper/css import swiper/css/navigation import swiper/css/paginationimport { Navigation, Pagination, Scrollbar, A11y, Autoplay, EffectCreative } from swiper/modules;import { Swiper, SwiperSlide, } from swiper/react; 普通版本 重点ÿ…...

零基础Linux_23(多线程)线程安全+线程互斥(加锁)+死锁
目录 1. 线程安全 1.1 线程不安全前期 1.2 线程不安全原因 2. 线程互斥 2.1 加锁保护(代码) 2.2 锁的本质 3. 可重入对比线程安全 4. 死锁 4.1 死锁的必要条件 4.2 避免死锁 5. 笔试面试题 答案及解析 本篇完。 1. 线程安全 基于上一篇线程…...
【算法|贪心算法系列No.5】leetcode409. 最长回文串
个人主页:兜里有颗棉花糖 欢迎 点赞👍 收藏✨ 留言✉ 加关注💓本文由 兜里有颗棉花糖 原创 收录于专栏【手撕算法系列专栏】【LeetCode】 🍔本专栏旨在提高自己算法能力的同时,记录一下自己的学习过程,希望…...
【Linux】安装与配置虚拟机及虚拟机服务器坏境配置与连接---超详细教学
一,操作系统介绍 1.1.什么是操作系统 操作系统(Operating System,简称OS)是一种系统软件,它是计算机硬件和应用软件之间的桥梁。它管理计算机的硬件和软件资源,为应用程序提供接口和服务,并协…...

机器学习实验一:KNN算法,手写数字数据集(使用汉明距离)(2)
KNN-手写数字数据集: 使用sklearn中的KNN算法工具包( KNeighborsClassifier)替换实现分类器的构建,注意使用的是汉明距离; 运行结果:(大概要运行4分钟左右) 代码: import pandas as…...
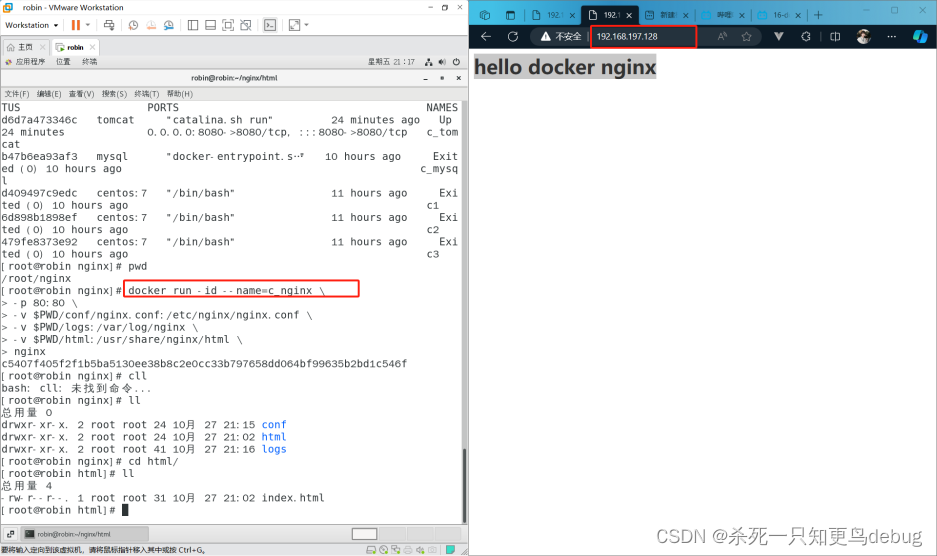
docker应用部署---nginx部署的配置
1. 搜索nginx镜像 docker search nginx2. 拉取nginx镜像 docker pull nginx3. 创建容器,设置端口映射、目录映射 # 在/root目录下创建nginx目录用于存储nginx数据信息 mkdir ~/nginx cd ~/nginx mkdir conf cd conf# 在~/nginx/conf/下创建nginx.conf文件,粘贴下…...

Sql Server中的表组织和索引组织(聚集索引结构,非聚集索引结构,堆结构)
正文 SqlServer用三种方法来组织其分区中的数据或索引页: 1、聚集索引结构 聚集索引是按B树结构进行组织的,B树中的每一页称为一个索引节点。每个索引行包含一个键值和一个指针。指针指向B树上的某一中间级页(比如根节点指向中间级节点中的…...

C++类对象反制机制实现_精简修改版
前几天写的类对象反射机制太烦锁了,今天写个修改版的,精简为两个类 一个是类的数据结构,另一个是类的父类对象,把所有操作类的方法都写到父类中 1.类的信息结构体 struct Field_Node {TCHAR m_name[20]; //字段名称TCHAR m_typeName[20]; // 字段类型名称size_t m_typeHashC…...

C#开发的IEnumerable接口
C#开发的IEnumerable接口 在前面分析中,我们会遇到下面这行代码: var refineries = self.World.ActorsWithTrait<IAcceptResources>() .Where(r => r.Actor != ignore && r.Actor.Owner == self.Owner && IsAcceptableProcType(r.Actor)) .Select…...
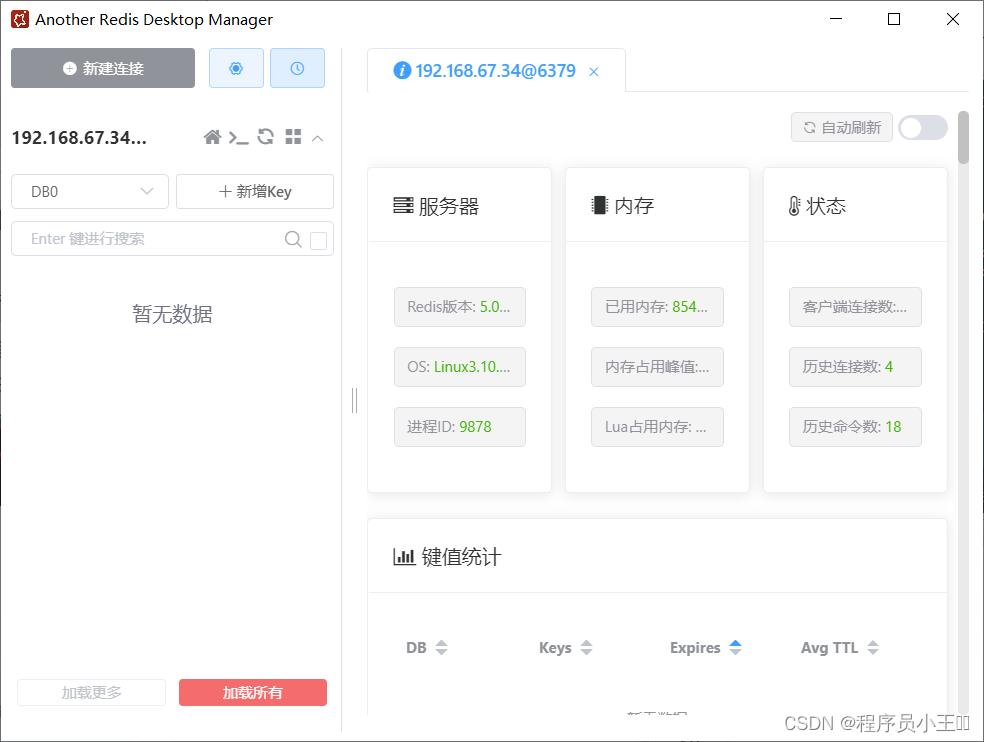
Redis详细安装教程
目录 一、Redis 的安装及启动停止1-1 下载 redis的压缩包1-2 开始解压 redis1-3 执行 make 命令编译1-4 启动 redis修改配置文件1-5 设置远程连接1-6 设置后台启动1-7 设置密码1-8 配置服务启动(使用 systemctl 的方法)启动 redis配置开机启动操作redis使…...
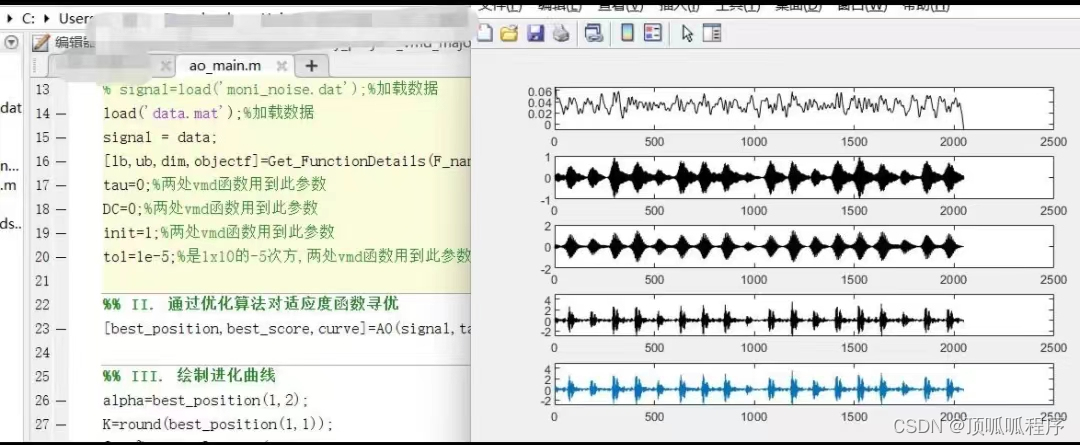
36基于matlab的对分解层数和惩罚因子进行优化
基于matlab的对分解层数和惩罚因子进行优化。蚁狮优化算法优化VMD,算术优化算法优化VMD,遗传优化算法优化VMD,灰狼优化算法优化VMD,海洋捕食者优化算法优化VMD,粒子群优化VMD,麻雀优化算法优化VMD,鲸鱼优化…...
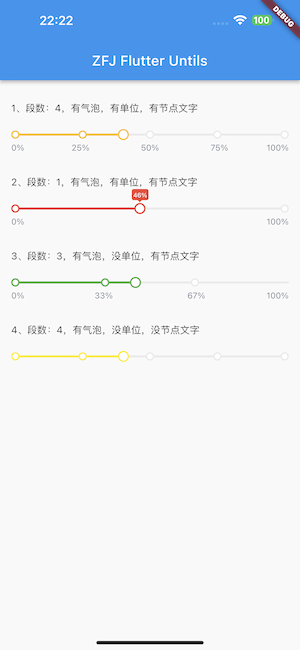
【Flutter】自定义分段选择器Slider
【Flutter】ZFJ自定义分段选择器Slider 前言 在开发一个APP的时候,需要用到一个分段选择器,系统的不满足就自己自定义了一个; 可以自定义节点的数量、自定义节点的大小、自定义滑竿的粗细,自定义气泡的有无等等… 基本上满足你…...

【软考系统架构设计师】2023年系统架构师冲刺模拟习题之《软件工程》
在软考中软件工程模块主要包含以下考点: 文章目录 软件过程模型🌟🌟🌟🌟逆向工程🌟基于构件的软件工程🌟🌟软件开发与软件设计与维护净室软件工程软件模型软件需求 软件过程模型&am…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...
