Leetcode---368周赛
题目列表
2908. 元素和最小的山形三元组 I
2909. 元素和最小的山形三元组 II
2910. 合法分组的最少组数
2911. 得到 K 个半回文串的最少修改次数
一、元素和最小的山形三元组I


没什么好说的,不会其他方法就直接暴力,时间复杂度O(n^3),代码如下
class Solution {
public:int minimumSum(vector<int>& nums) {int n=nums.size();int ans=INT_MAX;for(int i=0;i<n;i++)for(int j=i+1;j<n;j++)for(int k=j+1;k<n;k++)if(nums[i]<nums[j]&&nums[j]>nums[k])ans=min(ans,nums[i]+nums[j]+nums[k]);return ans==INT_MAX?-1:ans;}
};二、元素和最小的山形三元组II
这题和上一题一样,只是数据范围变大,需要优化时间复杂度,这也是老套路了,直接先预处理出前后缀最小值就行,然后枚举中间的那个元素,O(n)时间复杂度,代码如下
class Solution {
public:int minimumSum(vector<int>& nums) {int n=nums.size(),ans=INT_MAX;int suf[n];suf[n-1]=nums.back();for(int i=n-2;i>=0;i--)suf[i]=min(suf[i+1],nums[i]);for(int i=1,pre=nums[0];i<n-1;i++){if(pre<nums[i]&&nums[i]>suf[i+1])ans=min(ans,pre+nums[i]+suf[i+1]);pre=min(pre,nums[i]);}return ans==INT_MAX?-1:ans;}
};三、合法分组的最少组数
这题还是有点难度的,但是思路还是很明显,先统计数字出现的次数,然后对相同数字进行分组,使得分出的组满足两个条件。关键是如何满足这两个条件,第一个已经满足了,主要看第二个
而第二个条件,其实已经在提醒我们需要枚举分组数量了,因为它限制了每个组的数量只能是x/x+1,都限定这么死了,你不枚举真的是可惜了,当然有人会想到二分,其实这题如果是枚举每个组的数量的话,是不满足二段性的(如果有能二分的方法,欢迎大家在评论区留言)
那么我来举个例子讲讲为什么不能二分?即为什么不满足二段性?其实我们在想二段性的时候,应该能感觉的出来这个二段性不是很"明确",因为它能被分成每组两个元素,和它能被分成每组三个元素没有必然关系,下面举个例子
假设我们要将7个1分成最少组,很显然如果每组的个数是7/8,肯定可以,如果每组的个数是6/7也是可以的,如果每组的个数是5/6,就不可以了,但是如果每组的个数是3/4,那么又可以了,所以不具有二段性,所以我们选择从大往小枚举,遇到的第一个符合条件的个数就是最优解
有人可能会对上面的枚举方法感到奇怪,会觉得枚举7/8和枚举6/7,这两个7是不是重复了?你如果单看那种能被7整除的数,那么当然是重复的,如果是那些不能被7整除的数,那么和7搭配的6/8就是两种不同组合方式
那么我们如何判断一个数y能否由x/x+1这两个数组合而成呢?即y=ax+b(x+1),要求a+b的值尽可能小(如果数学好,这题也已经被秒了,本质就是exgcd),如果数学不好,怎么办?
我们来想一想,如果我们要让分配的每个组的个数相差为1,其实就是让y平均分配到每组(注意这里的平均要求分出的组的个数最少),我们先用y/(x+1)得到n组,剩下m=y%(x+1)个,如果m+n>=x,那么我们可以从n中的m组各自拿出一个1,使得剩下的元素个数也符合条件,这样就能得到最少的分配组数,而如果m+n<x,显然这是不符合条件的
那么这时有人就会有另一个想法:如果我们先用y/x得到n组,剩余m=y/x个,如果m<=n就符合条件,如果m>n就不符合条件,是不是也行呢?看似和上面的想法很契合,很相似,但是这是不行的,不信可以去写一下代码试试,你会在[10,10,10,3,1,1]这个样例挂掉,这里简单说明一下原因,这n/k不能保证是最小分组,因为我们是每次的分组方案是k/k+1,你用n/k的结果其实和n/(k+1)天差地别,如果n=20,k=4,用n/k得到最小分组数为5,但是n/(k+1)的最小分组数却是4,更别说n更大了,只会相差越来越多,这里本质还是没有明白上面绿色的句子,即怎么平均才能让分出的组的个数尽可能的少?好好理解一下
代码如下
class Solution {
public:int minGroupsForValidAssignment(vector<int>& nums) {unordered_map<int,int>cnt;int m=INT_MAX;for(auto& e:nums) cnt[e]++;if(cnt.size()==1) return 1;for(auto&[a,c]:cnt) m=min(m,c);int ans=INT_MAX;function<bool(int)>check=[&](int k)->bool{int res=0;for(auto&[a,c]:cnt){int mod=c%(k+1);int x=c/(k+1);if(mod==0)res+=x;else if(k<=mod+x)res=res+x+1;elsereturn false;}ans=min(ans,res);return true;};for(int i=m;i>=1;i--){if(check(i))break;}return ans;}
};四、得到k个半回文串的最小修改次数
这题主要是概念比较唬人,这个半回文串估计很多人都看蒙了,这里建议结合样例多手玩一下,基本上就懂了,这里就不对这个概念做深入讨论了,这里提醒一下,子串的长度>=2
这题其实不复杂,只要预处理一下每个数的真因子和每个子串变成半回文串需要修改的最小字符数,然后一个动态规划看看怎么划分子串就行了,关键是你能不能将思路写成代码
//预处理出每个数的真因子
int MX=201;
vector<vector<int>>v(MX);
int init=[](){for(int i=1;i<MX;i++)for(int j=2*i;j<MX;j+=i)v[j].push_back(i);return 0;
}();
class Solution {
public://计算每个子串变成半回文串的需要修改的最小字符数int get_min(const string& s){int n=s.size();int res=n;for(int d:v[n]){//枚举因子进行划分int m=0;for(int j=0;j<d;j++){//枚举每一个子序列for(int l=j,r=n-d+j;l<r;l+=d,r-=d){//计算每个子序列变成回文串需要修改的字符数m+=(s[l]!=s[r]);}}res=min(res,m);}return res;}int minimumChanges(string s, int k) {int n=s.size();vector<vector<int>>modify(n,vector<int>(n));//计算每个子串的最小修改次数for(int l=0;l<n-1;l++){for(int r=l+1;r<n;r++){modify[l][r]=get_min(s.substr(l,r-l+1));}}vector<vector<int>>memo(n,vector<int>(k,n+1));//n+1代表没有计算过,因为字符串最多只有n个元素,不可能需要修改n+1次function<int(int,int)>dfs=[&](int r,int k)->int{if(k==0) return modify[0][r];if(memo[r][k]<=n) return memo[r][k];int res=INT_MAX;for(int l=r-1;l>=2*k;l--){res=min(res,dfs(l-1,k-1)+modify[l][r]);}return memo[r][k]=res;};return dfs(n-1,k-1);//动态规划//vector<vector<int>>dp(k,vector<int>(n));//dp[0]=modify[0];//for(int i=1;i<k;i++){// for(int r=2*i+1;r<n;r++){// int res=INT_MAX;// for(int l=r-1;l>=2*i;l--){// res=min(res,dp[i-1][l-1]+modify[l][r]);// }// dp[i][r]=res;// }//}//return dp[k-1][n-1];}
};
相关文章:

Leetcode---368周赛
题目列表 2908. 元素和最小的山形三元组 I 2909. 元素和最小的山形三元组 II 2910. 合法分组的最少组数 2911. 得到 K 个半回文串的最少修改次数 一、元素和最小的山形三元组I 没什么好说的,不会其他方法就直接暴力,时间复杂度O(n^3),代…...
矢量图形编辑软件Illustrator 2023 mac中文版软件特点(ai2023) v27.9
illustrator 2023 mac是一款矢量图形编辑软件,用于创建和编辑排版、图标、标志、插图和其他类型的矢量图形。 illustrator 2023 mac软件特点 矢量图形:illustrator创建的图形是矢量图形,可以无限放大而不失真,这与像素图形编辑软…...

一、Docker Compose——什么是 Docker Compose
Docker Compose 是一个用来定义和运行多容器 Docker 应用程序的工具,他的方便之处就是可以使用 YAML 文件来配置将要运行的 Docker 容器,然后使用一条命令即可创建并启动配置好的 Docker 容器了;相比手动输入命令的繁琐,Docker Co…...

Java提升技术,进阶为高级开发和架构师的路线
原文网址:Java提升技术,进阶为高级开发和架构师的路线-CSDN博客 简介 Java怎样提升技术?怎样进阶为高级开发和架构师?本文介绍靠谱的成长路线。 首先点明,只写业务代码是无法成长技术的。提升技术的两个方法是&…...

记一次 .Net+SqlSugar 查询超时的问题排查过程
环境和版本:.Net 6 SqlSuger 5.1.4.* ,数据库是mysql 5.7 ,数据量在2000多条左右 业务是一个非常简单的查询,代码如下: var list _dbClient.Queryable<tb_name>().ToList(); tb_name 下配置了一对多的关系…...
PHP危险函数
PHP危险函数 文章目录 PHP危险函数PHP 代码执行函数eval 语句assert()语句preg_replace()函数正则表达式里修饰符 回调函数call_user_func()函数array_map()函数 OS命令执行函数system()函数exec()函数shell_exec()函数passthru() 函数popen 函数反引号 实列 通过构造函数可以执…...

【ARM Cortex-M 系列 4 番外篇 -- 常用 benchmark 介绍】
文章目录 1.1 CPU 性能测试 MIPS 计算1.1.1 Cortex-M7 CPI 1.2 benchmark 小节1.3.1 Geekbenck 介绍 1.3 编译参数配置 1.1 CPU 性能测试 MIPS 计算 每秒百万指令数 (MIPS):在数据压缩测试中,MIPS 每秒测量一次 CPU 执行的低级指令的数量。越高越好&…...
web安全-原发抗抵赖
原发抗抵赖 原发抗抵赖也称不可否认性,主要表现以下两种形式: 数据发送者无法否认其发送数据的事实。例如,A向B发信,事后,A不能否认该信是其发送的。数据接收者事后无法否认其收到过这些数据。例如,A向B发…...

强化学习------PPO算法
目录 简介一、PPO原理1、由On-policy 转化为Off-policy2、Importance Sampling(重要性采样)3、off-policy下的梯度公式推导 二、PPO算法两种形式1、PPO-Penalty2、PPO-Clip 三、PPO算法实战四、参考 简介 PPO 算法之所以被提出,根本原因在于…...
express框架)
node(三)express框架
文章目录 1.express介绍2.express初体验3.express路由3.1什么是路由?3.2路由的使用 1.express介绍 是一个基于Node平台的极简、灵活的WEB应用开发框架,官网地址:https://www.expressjs.com.cn/ 简单来说,express是一个封装好的工…...

linux find命令搜索日志内容
linux find命令搜索日志内容 查询服务器log日志 find /opt/logs/ -name "filename.log" | xargs grep -a "这里是要查询的字符"加上-a 是为了不报查出 binary 的错 服务器会返回 包含所查字符的整行日志信息...

CentOS 编译安装TinyXml2
安装 TinyXml2 Git 源码下载地址:https://github.com/leethomason/tinyxml2 步骤1:首先,你需要下载tinyxml2的源代码。你可以从Github或者源代码官方网站下载。并上传至/usr/local/source_code/ 步骤2:下载完成后,需要将源代码解…...

竞赛选题 深度学习人体跌倒检测 -yolo 机器视觉 opencv python
0 前言 🔥 优质竞赛项目系列,今天要分享的是 🚩 **基于深度学习的人体跌倒检测算法研究与实现 ** 该项目较为新颖,适合作为竞赛课题方向,学长非常推荐! 🥇学长这里给一个题目综合评分(每项满…...

使用gson将复杂的树型结构转Json遇到的问题,写入文件为空
某个项目需要用到一个较为复杂的数据结构。定义成一个树型链表。 public class TreeNode { private String name; public String getName() { return name; } public void setName(String name) { this.name name; } public String getPartType() { retur…...

JavaScript异步编程:提升性能与用户体验
目录 什么是异步编程? 回调函数 Promise Async/Await 总结 在Web开发中,处理耗时操作是一项重要的任务。如果我们在执行这些操作时阻塞了主线程,会导致页面失去响应,用户体验下降。JavaScript异步编程则可以解决这个问题&…...
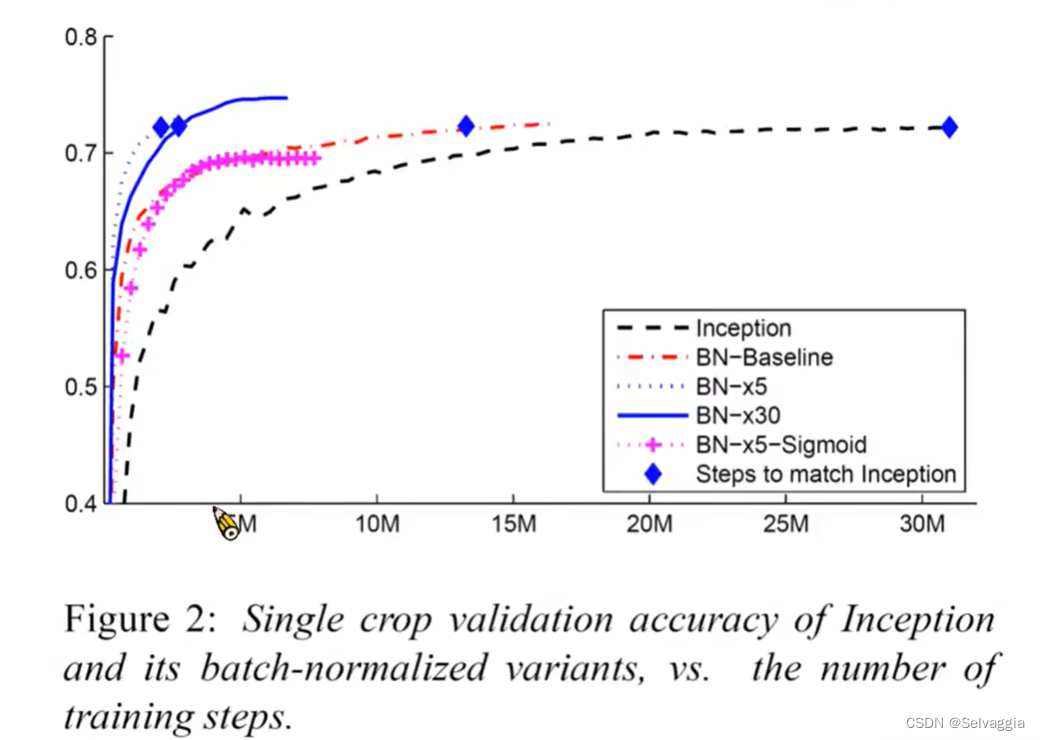
lossBN
still tips for learning classification and regression关于softmax的引入和作用分类问题损失函数 - MSE & Cross-entropy⭐Batch Normalization(BN)⭐想法:直接改error surface的landscape,把山铲平feature normalization那…...

【微信小程序】数字化会议OA系统之投票模块(附源码)
🎉🎉欢迎来到我的CSDN主页!🎉🎉 🏅我是Java方文山,一个在CSDN分享笔记的博主。📚📚 🌟推荐给大家我的专栏《微信小程序开发实战》。🎯Ἲ…...

clang-前端插件-给各种无花括号的“块”加花括号-基于llvm15--clang-plugin-add-brace
处理的语句 case 术语约定或备忘 case起止范围: 从冒号到下一个’case’开头, 简称有: case内 、case内容Ast: Abstract syntax tree: 抽象语法树没插入花括号的case 若case内, 以下任一条成立,则 跳过该case 即 不会对该case内容用花括号包裹. 有#define、有#include、有…...
实例小记)
python爬虫-某政府网站加速乐(简单版)实例小记
# -*- coding:utf-8 -*- # Time : 2023/10/23 17:06 # Author: 水兵没月 # File : 哈哈哈哈.py # Software: PyCharm ####################import random import requests# 代理 def get_proxy(proxy_typerandom.choice([1,2,3,4,5])):url "http://ZZZZZZZZZZZZZZZZZZ&qu…...
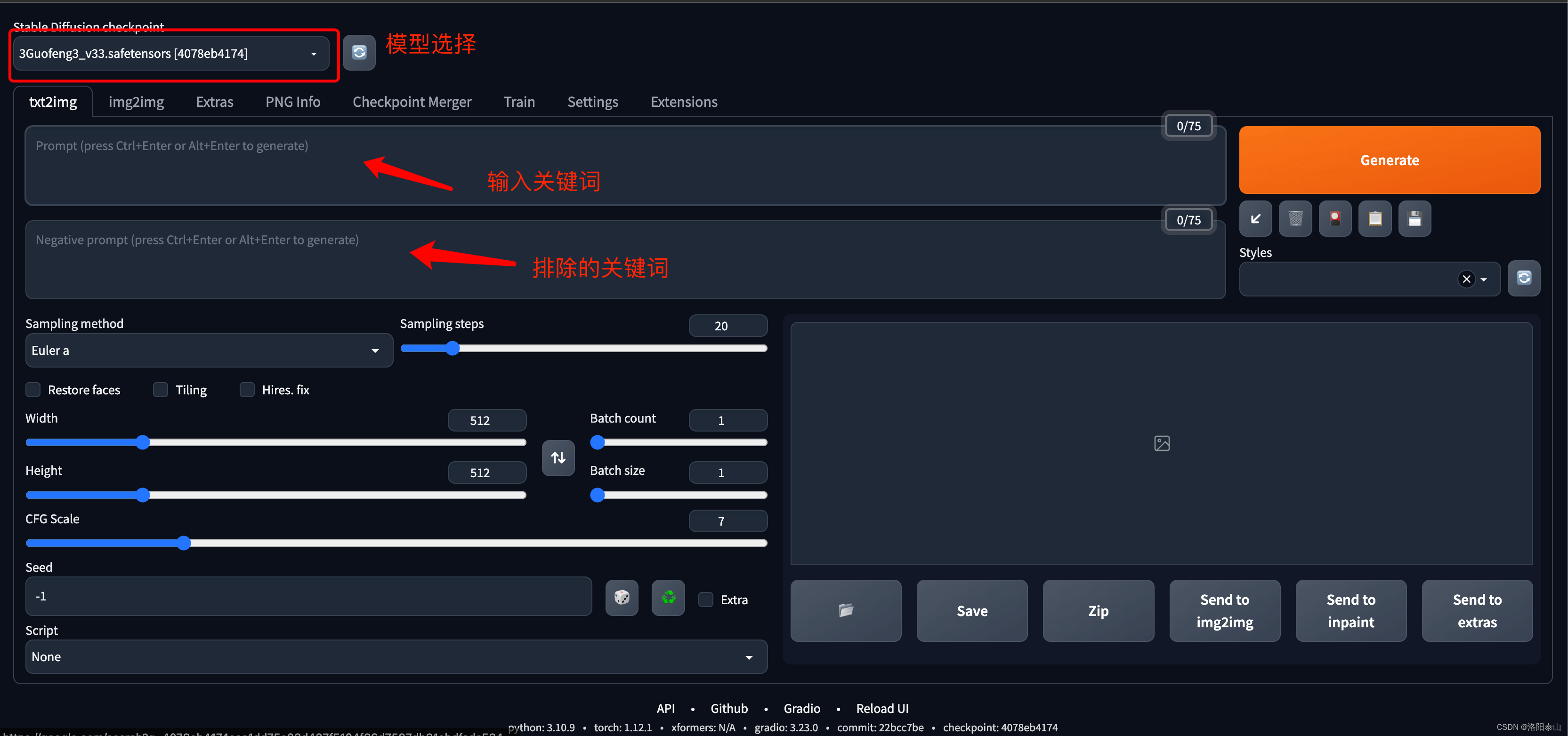
stable diffusion简介和原理
Stable Diffusion中文的意思是稳定扩散,本质上是基于AI的图像扩散生成模型。 Stable Diffusion是一个引人注目的深度学习模型,它使用潜在扩散过程来生成图像,允许模型在生成图像时考虑到文本的描述。这个模型的出现引起了广泛的关注和讨论&am…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...