【LeetCode每日一题合集】2023.10.16-2023.10.22(只出现一次的数字Ⅲ)
文章目录
- 260. 只出现一次的数字 III⭐(异或)🐂
- 2652. 倍数求和
- 解法1——枚举模拟
- 解法2—— O ( 1 ) O(1) O(1)容斥原理
- 相似题目——1201. 丑数 III(二分查找+容斥原理)
- 2530. 执行 K 次操作后的最大分数
- 解法1——贪心+优先队列
- 解法2—— O ( 1 ) O(1) O(1)空间原地堆化
- 1726. 同积元组(哈希表+组合数学)
- 2525. 根据规则将箱子分类(按题意模拟,分类讨论)
- 2316. 统计无向图中无法互相到达点对数
- 解法1——并查集
- 解法2——dfs求连通块大小
- 1402. 做菜顺序
- 解法1——动态规划
- 解法2——贪心⭐
260. 只出现一次的数字 III⭐(异或)🐂
https://leetcode.cn/problems/single-number-iii/description/?envType=daily-question&envId=2023-10-16
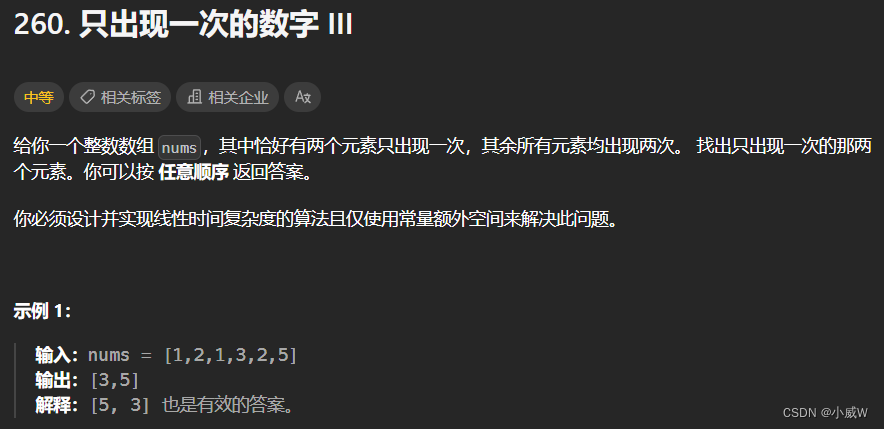
提示:
2 <= nums.length <= 3 * 10^4
-2^31 <= nums[i] <= 2^31 - 1
除两个只出现一次的整数外,nums 中的其他数字都出现两次
类似分治的思想。
先将数组全部异或,得出的结果是两个只出现一次数字的异或结果。
其中一定有1,因为这两个数字不同。
取出其最低位的1作为判断标准对原数组分组(实际上任意位的1都可以),分成的两组分别包括这两个只出现一次的数字。
这样就把问题转换成了两个 136. 只出现一次的数字
class Solution {public int[] singleNumber(int[] nums) {int xor = 0;for (int num: nums) xor ^= num;int mask = xor & (-xor); // 获取最低位的1int[] ans = new int[2];for (int num: nums) {if ((num & mask) == 0) ans[0] ^= num;else ans[1] ^= num;}return ans;}
}
2652. 倍数求和
https://leetcode.cn/problems/sum-multiples/description/?envType=daily-question&envId=2023-10-17
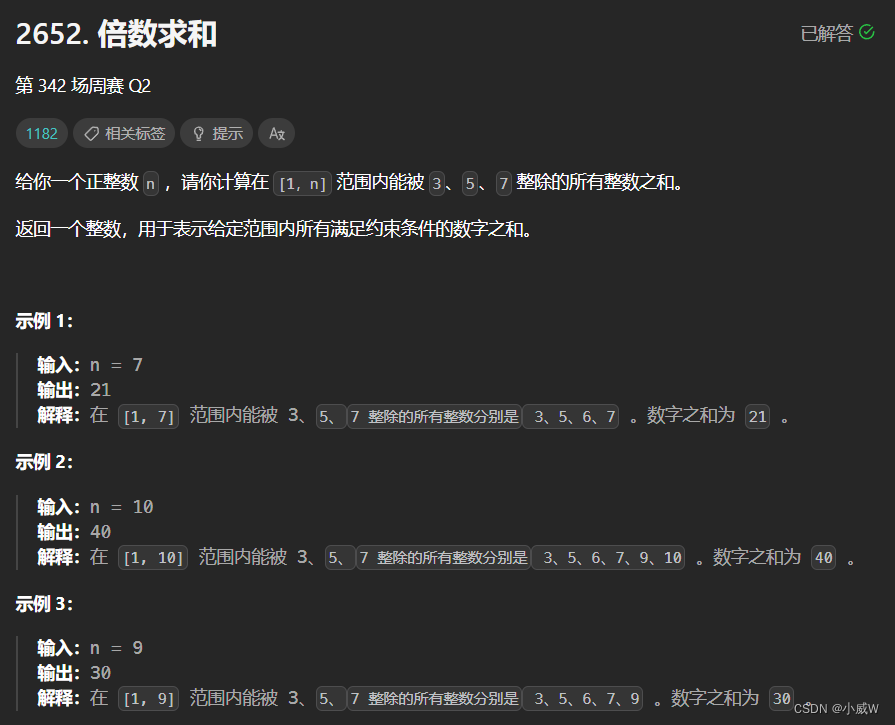
提示:
1 <= n <= 10^3
解法1——枚举模拟
class Solution {public int sumOfMultiples(int n) {int ans = 0;for (int i = 1; i <= n; ++i) {if (i % 3 == 0 || i % 5 == 0 || i % 7 == 0) ans += i;}return ans;}
}
解法2—— O ( 1 ) O(1) O(1)容斥原理
class Solution {int n;public int sumOfMultiples(int n) {this.n = n;return s(3) + s(5) + s(7) - s(15) - s(21) - s(35) + s(105);}// 计算从x~(n/x)x,共n/x项public int s(int x) {return n / x * (x + n / x * x) / 2;}
}
相似题目——1201. 丑数 III(二分查找+容斥原理)
https://leetcode.cn/problems/ugly-number-iii/description/
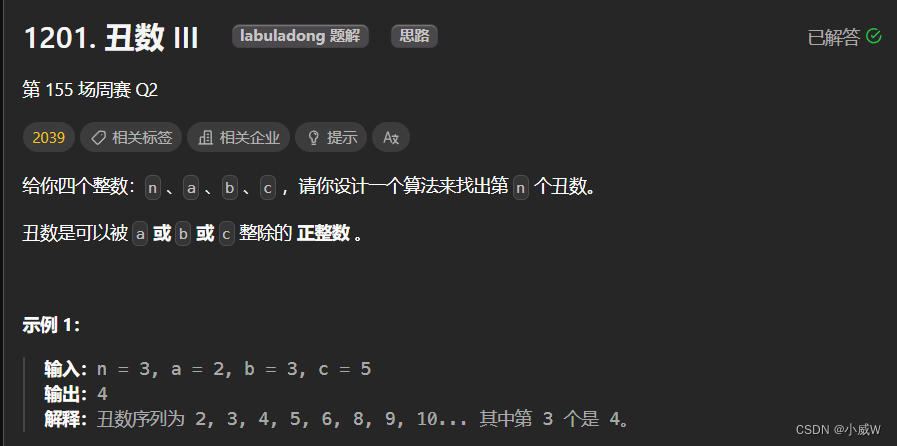
提示:
1 <= n, a, b, c <= 10^9
1 <= a * b * c <= 10^18
本题结果在 [1, 2 * 10^9] 的范围内
为什么会想到二分?
因为直接求答案不好求,但是我们可以判断1~x的范围内是否有n个丑数。
class Solution {public int nthUglyNumber(int n, int a, int b, int c) {long x = lcm(a, b), y = lcm(b, c), z = lcm(a, c), q = lcm(x, y);long l = 1, r = (long)2e9;while (l < r) {long mid = l + r >> 1;long aa = mid / a, bb = mid / b, cc = mid / c, xx = mid / x, yy = mid / y, zz = mid / z, qq = mid / q;long s = aa + bb + cc - xx - yy - zz + qq;if (s < n) l = mid + 1;else r = mid;}return (int)l;}public long gcd(long a, long b) {return b == 0? a: gcd(b, a % b);}public long lcm(long a, long b) {return a / gcd(a, b) * b;}
}
2530. 执行 K 次操作后的最大分数
https://leetcode.cn/problems/maximal-score-after-applying-k-operations/description/?envType=daily-question&envId=2023-10-18
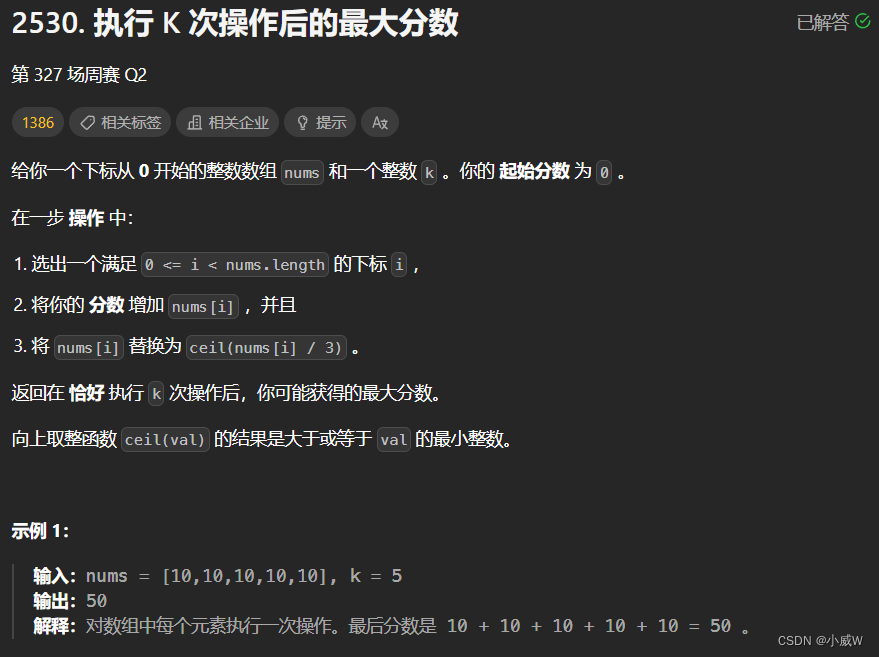
提示:
1 <= nums.length, k <= 10^5
1 <= nums[i] <= 10^9
解法1——贪心+优先队列
每次增加最大的数字即可。
class Solution {public long maxKelements(int[] nums, int k) {long ans = 0;PriorityQueue<Integer> pq = new PriorityQueue<>((a, b) -> b - a);for (int num: nums) pq.offer(num);for (int i = 0; i < k; ++i) {int c = pq.poll();ans += c;pq.offer((c + 2) / 3);}return ans;}
}
解法2—— O ( 1 ) O(1) O(1)空间原地堆化
https://leetcode.cn/problems/maximal-score-after-applying-k-operations/solutions/2487446/o1-kong-jian-zuo-fa-pythonjavacgojsrust-ztx6f/?envType=daily-question&envId=2023-10-18
原地堆化,把 nums 数组当成一个堆。
从 h.length / 2 - 1 开始倒序下沉。
class Solution {public long maxKelements(int[] nums, int k) {heapify(nums);long ans = 0;while (k-- > 0) {ans += nums[0];nums[0] = (nums[0] + 2) / 3;sink(nums, 0); // 下沉}return ans;}// 保证h[0]>=max(h[2*i+1],h[2*i+2])public void heapify(int[] h) {for (int i = h.length / 2 - 1; i >= 0; --i) {sink(h, i);}}public void sink(int[] h, int i) {int n = h.length;while (2 * i + 1 < n) {// 挑选左右儿子中更大的和i交换int j = 2 * i + 1; // i的左儿子if (j + 1 < n && h[j + 1] > h[j]) j++;if (h[j] <= h[i]) break; // 停止下沉swap(h, i, j);i = j;}}public void swap(int[] h, int i, int j) {int tmp = h[i];h[i] = h[j];h[j] = tmp;}
}
1726. 同积元组(哈希表+组合数学)
https://leetcode.cn/problems/tuple-with-same-product/description/
提示:
1 <= nums.length <= 1000
1 <= nums[i] <= 10^4
nums 中的所有元素 互不相同
计算出数组中所有两两组合的乘积的各个数量。
那么各个成绩的组合数就是 C x 2 = x ∗ ( x − 1 ) C_x^2=x*(x-1) Cx2=x∗(x−1),即任选两组。每种组合4个数字可以任意排位置,最后结果*4。
class Solution {public int tupleSameProduct(int[] nums) {int n = nums.length, ans = 0;Map<Integer, Integer> cnt = new HashMap<>();for (int i = 0; i < n; ++i) {for (int j = i + 1; j < n; ++j) {cnt.merge(nums[i] * nums[j], 1, Integer::sum);}}for (int v: cnt.values()) {if (v > 1) ans += v * (v - 1);}return ans * 4;}
}
2525. 根据规则将箱子分类(按题意模拟,分类讨论)
https://leetcode.cn/problems/categorize-box-according-to-criteria/description/?envType=daily-question&envId=2023-10-20
提示:
1 <= length, width, height <= 10^5
1 <= mass <= 10^3
class Solution {public String categorizeBox(int length, int width, int height, int mass) {boolean bulky = false, heavy = false;if (length >= 10000 || width >= 10000 || height >= 10000 || mass >= 10000 || (long)length * width * height >= 1000000000) bulky = true;if (mass >= 100) heavy = true; if (bulky && heavy) return "Both";if (!bulky && !heavy) return "Neither";if (bulky) return "Bulky";return "Heavy";}
}
2316. 统计无向图中无法互相到达点对数
https://leetcode.cn/problems/count-unreachable-pairs-of-nodes-in-an-undirected-graph/description/?envType=daily-question&envId=2023-10-21
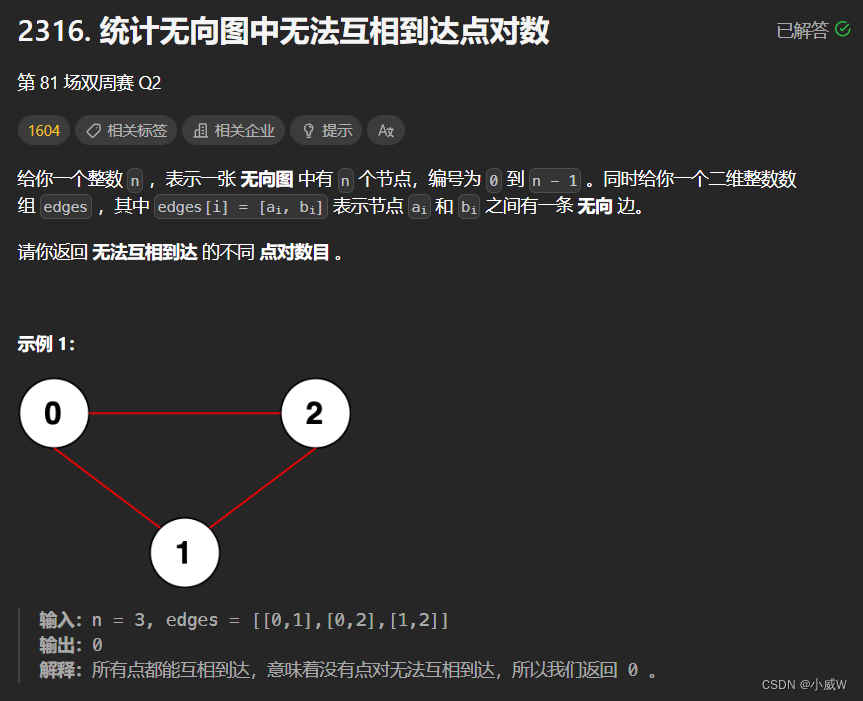
提示:
1 <= n <= 10^5
0 <= edges.length <= 2 * 10^5
edges[i].length == 2
0 <= ai, bi < n
ai != bi
不会有重复边。
解法1——并查集
关于并查集可见:【算法基础:数据结构】2.3 并查集
并查集得出各个联通集合中元素的数量,不同集合中的元素都可以两两组合。
class Solution {public long countPairs(int n, int[][] edges) {long ans = 0;// 并查集int[] p = new int[n];Arrays.setAll(p, e -> e);for (int[] e: edges) {if (p[e[0]] != p[e[1]]) p[find(p, e[0])] = find(p, e[1]);}// 记录每个集合中的元素个数Map<Integer, Integer> cnt = new HashMap<>();for (int i = 0; i < n; ++i) {cnt.merge(find(p, i), 1, Integer::sum);}for (int v: cnt.values()) {ans += (long)v * (n - v); // 和其它所有集合的一一对应}return ans / 2; // 结果除以2去掉重复计算的}public int find(int[]p, int x) {if (p[x] != x) p[x] = find(p, p[x]);return p[x];}
}
解法2——dfs求连通块大小
class Solution {public long countPairs(int n, int[][] edges) {long ans = 0, total = 0;List<Integer>[] g = new ArrayList[n];boolean[] st = new boolean[n];Arrays.setAll(g, e -> new ArrayList<Integer>());for (int[] e: edges) {g[e[0]].add(e[1]);g[e[1]].add(e[0]);}for (int i = 0; i < n; ++i) {if (!st[i]) {int cnt = dfs(g, st, i); // dfs计算连通块大小ans += total * cnt;total += cnt;}}return ans;}public int dfs(List<Integer>[] g, boolean[] st, int x) {int res = 1;st[x] = true;for (int y: g[x]) {if (!st[y]) {res += dfs(g, st, y);}}return res;}
}
1402. 做菜顺序
https://leetcode.cn/problems/reducing-dishes/description/?envType=daily-question&envId=2023-10-22
提示:
n == satisfaction.length
1 <= n <= 500
-1000 <= satisfaction[i] <= 1000
解法1——动态规划
dp[i][j] 表示前 i+1 个菜,选择 j 个时的值。
最后结果是前 n 个菜中,选择 0~n 个时的最大值。
class Solution {public int maxSatisfaction(int[] satisfaction) {int n = satisfaction.length;int[][] dp = new int[n + 1][n + 1];Arrays.sort(satisfaction);dp[0][1] = satisfaction[0];for (int i = 1; i < n; ++i) {for (int j = 1; j <= i + 1; ++j) {dp[i][j] = dp[i - 1][j - 1] + satisfaction[i] * j;}}return Arrays.stream(dp[n - 1]).max().getAsInt();}
}
解法2——贪心⭐
见:https://leetcode.cn/problems/reducing-dishes/solutions/198214/zuo-cai-shun-xu-by-leetcode-solution/?envType=daily-question&envId=2023-10-22
class Solution {public int maxSatisfaction(int[] satisfaction) {Arrays.sort(satisfaction);int ans = 0, s = 0;for (int i = satisfaction.length - 1; i >= 0; --i) {s += satisfaction[i];if (s <= 0) return ans;ans += s;}return ans;}
}
相关文章:

【LeetCode每日一题合集】2023.10.16-2023.10.22(只出现一次的数字Ⅲ)
文章目录 260. 只出现一次的数字 III⭐(异或)🐂2652. 倍数求和解法1——枚举模拟解法2—— O ( 1 ) O(1) O(1)容斥原理相似题目——1201. 丑数 III(二分查找容斥原理) 2530. 执行 K 次操作后的最大分数解法1——贪心优…...

尚硅谷大数据项目《在线教育之实时数仓》笔记003
视频地址:尚硅谷大数据项目《在线教育之实时数仓》_哔哩哔哩_bilibili 目录 第7章 数仓开发之ODS层 P015 第8章 数仓开发之DIM层 P016 P017 P018 P019 01、node001节点Linux命令 02、KafkaUtil.java 03、DimSinkApp.java P020 P021 P022 P023 第7章 数…...
【Linux】部署单体项目以及前后端分离项目(项目部署)
一、简介 以下就是Linux部署单机项目和前后端分离项目的优缺点,希望对你有所帮助。 1、Linux部署单机项目: 优点: 1.简化了系统管理:由于所有服务都在同一台机器上运行,因此可以简化系统管理和维护。 2.提高了性能&a…...

设计模式之门面模式
前言 什么是门面模式 门面模式是一种结构型设计模式,它提供了一个统一的接口,用来访问子系统中的一群接口。它定义了一个高层接口,让子系统更容易使用。这种模式常用于将一个复杂的子系统封装成一个简单的接口,使得客户端可以方…...
Postman的使用
Postman的使用 Postman断言Postman常用断言1、断言响应状态码2、断言包含某个字符串3、断言JSON数据4、Postman断言工作原理 Postman关联Postman自动关联创建环境 3、Postman参数化CSV文件JSON文件1、用例集的导入导出2、环境导出 Postman断言 让Postman工具代替人自动判断预期…...
QGIS008:QGIS拓扑检查、修改及验证
摘要:本文介绍使用QGIS拓扑检查器和几何图形检查器检查图层的拓扑错误,修改拓扑错误,并对修改后的图层进行错误验证。 实验数据: 链接:https://pan.baidu.com/s/1Vy2s-KYS-XJevqHNdavv9A?pwdf06o 提取码:…...

安装DBD-Oracle报错处理
cd DBD-Oracle-1.83 perl Makefile.PL make && make install make编译报错如下: /bin/ld: 找不到 -lnsl collect2: 错误:ld 返回 1 make: *** [Makefile:524:blib/arch/auto/DBD/Oracle/Oracle.so] 错误 1 [rootlocalhost DBD-Ora…...

【机器学习】KNN算法-鸢尾花种类预测
KNN算法-鸢尾花种类预测 文章目录 KNN算法-鸢尾花种类预测1. 数据集介绍2. KNN优缺点: K最近邻(K-Nearest Neighbors,KNN)算法是一种用于模式识别和分类的简单但强大的机器学习算法。它的工作原理非常直观:给定一个新数…...
--lora - lora驱动模块)
LuatOS-SOC接口文档(air780E)--lora - lora驱动模块
常量 常量 类型 解释 lora.SLEEP number SLEEP模式 lora.STANDBY number STANDBY模式 lora.init(ic, loraconfig,spiconfig) lora初始化 参数 传入值类型 解释 string lora 型号,当前支持: llcc68 sx1268 table lora配置参数,与具体设备…...

Compose 自定义 - 绘制 Draw
一、概念 所有的绘制操作都是通过调整像素大小来执行的。若要确保项目在不同的设备密度和屏幕尺寸上都能采用一致的尺寸,请务必使用 .toPx() 对 dp 进行转换或者采用小数尺寸。 二、Modifier 修饰符绘制 官方页面 在修饰的可组合项之上或之下绘制。 .drawWithCon…...

c#学习相关系列之构造函数
目录 一、构造函数的作用 二、构造函数的特征 三、三种构造函数介绍 1、实例构造函数 2、静态构造函数 3、私有构造函数 一、构造函数的作用 构造函数用来创建对象,并且可以在构造函数中对此对象进行初始化。构造函数具有与类相同的名称,它通常用来…...

CS224W1.3——图表示的选择
文章目录 1. 图网络构成2. 选择一个合适的表示3. 图结构实例3.1 二部图3.2 图的表示 4. 节点和边的属性 这小节主要讲图表示的选择。 1. 图网络构成 对于每个实体,我们创建节点 N N N,对于每个关系,我们创建边 E E E,对于整体而言…...

rust学习——插件rust-analyzer安装与配置
插件rust-analyzer安装与配置 rust-analyzer有一个中文版本。安装前请先卸载其他rust插件。 首次安装会下载语言服务。 您可能是首次安装Rust中文标准库插件 现在还需要安装Rust语言服务(约25MB单文件)就全部安装完成啦~正在后台自动安装请稍后... 下载完成...OK配置 "…...
Spring Boot简介
Spring Boot帮助你创建可以运行的独立的、基于Spring的生产级应用程序。 我们对Spring平台和第三方库采取了有主见的观点,这样你就能以最少的麻烦开始工作。 大多数Spring Boot应用程序只需要很少的Spring配置。 你可以使用Spring Boot来创建Java应用程序ÿ…...
Linux下protobuf和 protobuf-c安装使用
如果在 C语言中使用 protobuf,就需要使用 protobuf-c这个库。 protobuf使用详解:https://blog.csdn.net/qq_42402854/article/details/134066566 下面在 Linux下安装 protobuf和 protobuf-c。 一、下载 protobuf和 protobuf-c 官方的 Protocol Buffer提…...
FastAPI 快速学习之 Flask 框架对比
目录 一、前言二、FastAPI 优势三、Hello World四、HTTP 方法五、URL 变量六、查询字符串七、POST 请求八、文件上传九、表单提交十、Cookies十一、模块化视图十二、数据校验十三、自动化文档Swagger 风格ReDoc 风格 十四、CORS跨域 一、前言 本文主要对 FastAPI 与 Flask 框架…...

Spring Boot和XXL-Job:高效定时任务管理
Spring Boot和XXL-Job:高效定时任务管理 前言第一:XXL-Job简介什么是XXL-job对比别的任务调度 第二: springboot整合XXL-job配置XXL-Job Admin拉取XXL-Job代码修改拉取的配置 配置执行器自己的项目如何整合maven依赖properties文件配置执行器…...
3、QtCharts 动态曲线图
文章目录 效果声明变量构建静态图表创建计时器连接信号与槽槽函数核心代码 效果 声明变量 构建静态图表 //构建曲线系列m_splineSerisenew QSplineSeries(this);//为折线添加数据qreal x0.f;for (size_t i0;i<c_MaxSize;i){xqreal(i1)/c_MaxSize;m_splineSerise->append(…...
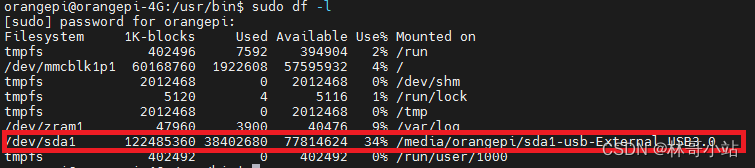
Linux下自动挂载U盘或者USB移动硬盘
最近在折腾用树莓派(实际上是平替香橙派orangepi zero3)搭建共享文件服务器,有一个问题很重要,如何在系统启动时自动挂载USB移动硬盘。 1 使用/etc/fstab 最开始尝试了用/etc/fstab文件下增加:"/dev/sda1 /home/orangepi/s…...
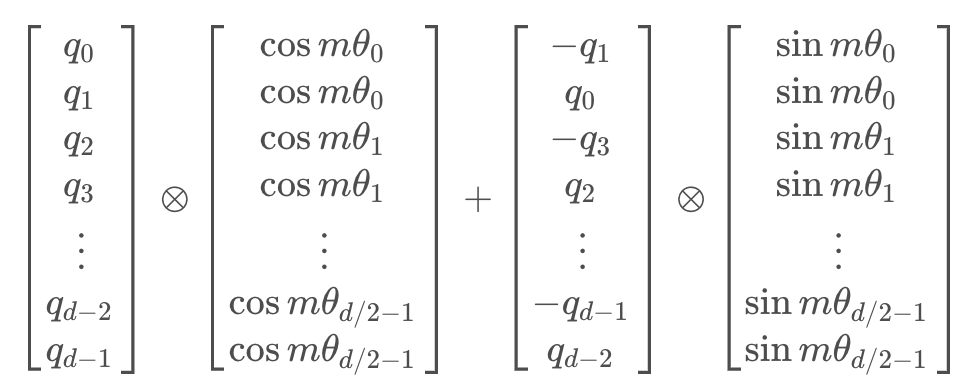
一文通透位置编码:从标准位置编码到旋转位置编码RoPE
前言 关于位置编码和RoPE 我之前在本博客中的另外两篇文章中有阐述过(一篇是关于LLaMA解读的,一篇是关于transformer从零实现的),但自觉写的不是特别透彻好懂再后来在我参与主讲的类ChatGPT微调实战课中也有讲过,但有些学员依然反馈RoPE不是…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...

土建施工员考试:建筑施工技术重点知识有哪些?
《管理实务》是土建施工员考试中侧重实操应用与管理能力的科目,核心考查施工组织、质量安全、进度成本等现场管理要点。以下是结合考试大纲与高频考点整理的重点内容,附学习方向和应试技巧: 一、施工组织与进度管理 核心目标: 规…...
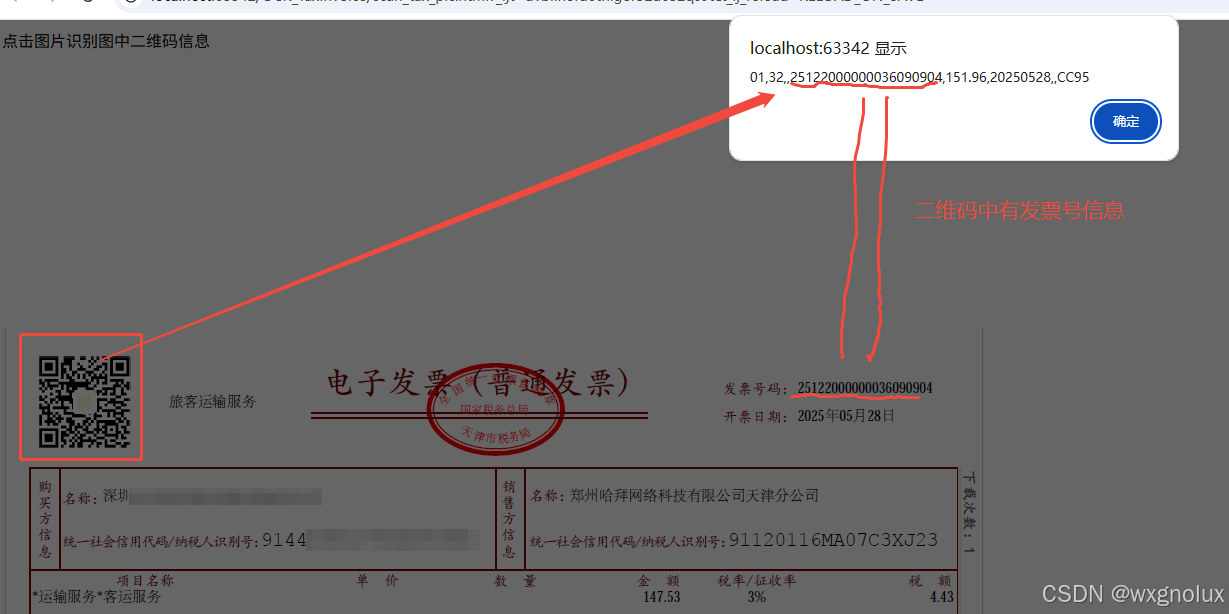
网页端 js 读取发票里的二维码信息(图片和PDF格式)
起因 为了实现在报销流程中,发票不能重用的限制,发票上传后,希望能读出发票号,并记录发票号已用,下次不再可用于报销。 基于上面的需求,研究了OCR 的方式和读PDF的方式,实际是可行的ÿ…...
