怒刷LeetCode的第28天(Java版)
目录
第一题
题目来源
题目内容
解决方法
方法一:动态规划
方法二:迭代
方法三:斐波那契数列公式
第二题
题目来源
题目内容
解决方法
方法一:栈
方法二:路径处理类
方法三:正则表达式
方法四:字符串处理
第三题
题目来源
题目内容
解决方法
方法一:动态规划
第一题
题目来源
70. 爬楼梯 - 力扣(LeetCode)
题目内容

解决方法
方法一:动态规划
可以使用动态规划的方法来解决这个问题。假设要爬到第n阶楼梯,那么可以从第n-1阶楼梯爬一步上来,或者从第n-2阶楼梯爬两步上来。因此,到达第n阶楼梯的方法数等于到达第n-1阶楼梯的方法数加上到达第n-2阶楼梯的方法数。
首先初始化前两个楼梯的方法数,即dp[0]=1和dp[1]=1。然后从第3个楼梯开始,通过迭代计算每个楼梯的方法数,直到第n个楼梯。
class Solution {
public int climbStairs(int n) {if (n <= 1) {return 1;}int[] dp = new int[n + 1];dp[0] = 1;dp[1] = 1;for (int i = 2; i <= n; i++) {dp[i] = dp[i - 1] + dp[i - 2];}return dp[n];
}
}
复杂度分析:
- 这个算法的时间复杂度是O(n),其中n是楼梯的阶数。这是因为我们需要计算从第2阶楼梯到第n阶楼梯的方法数,每次计算都需要常数时间。
- 空间复杂度是O(n),因为我们使用一个大小为n+1的数组来存储每个楼梯的方法数。如果只需要存储前两个楼梯的方法数,空间复杂度可以优化为O(1)。
总结起来,这个算法是相当高效的,可以在合理的时间内解决规模较大的问题。
LeetCode运行结果:
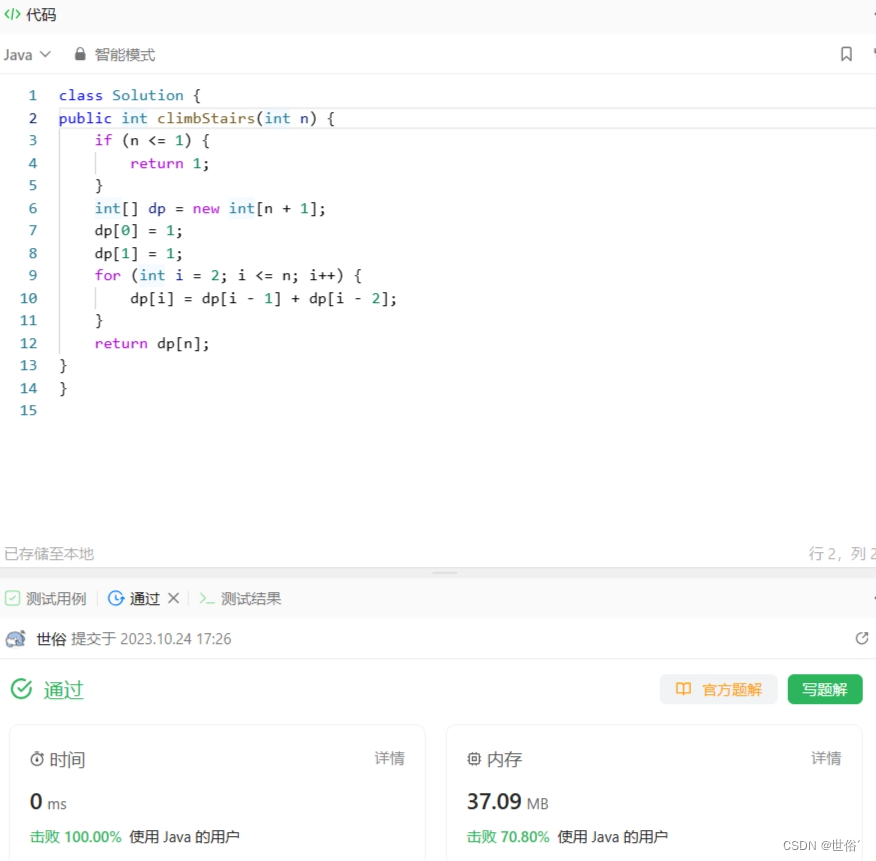
方法二:迭代
除了动态规划,还可以使用迭代的方法来解决这个问题。迭代方法的思路是从前往后计算每个楼梯的方法数,并利用一个变量来保存前两个楼梯的方法数,以便计算当前楼梯的方法数。
class Solution {
public int climbStairs(int n) {if (n <= 1) {return 1;}int prev1 = 1; // 到达前一个楼梯的方法数int prev2 = 1; // 到达前两个楼梯的方法数int current = 0; // 当前楼梯的方法数for (int i = 2; i <= n; i++) {current = prev1 + prev2;prev2 = prev1;prev1 = current;}return current;
}
}
复杂度分析:
- 时间复杂度: 在迭代方法中,我们使用一个循环来计算每个楼梯的方法数,循环执行了n-2次(从第3个楼梯开始计算)。因此,时间复杂度为O(n)。
- 空间复杂度: 在迭代方法中,我们只使用了三个变量:prev1、prev2和current来保存楼梯的方法数。这三个变量的空间占用是常量级别的,与输入规模n无关。因此,空间复杂度为O(1)。
综上所述,迭代方法的时间复杂度为O(n),空间复杂度为O(1)。
LeetCode运行结果:
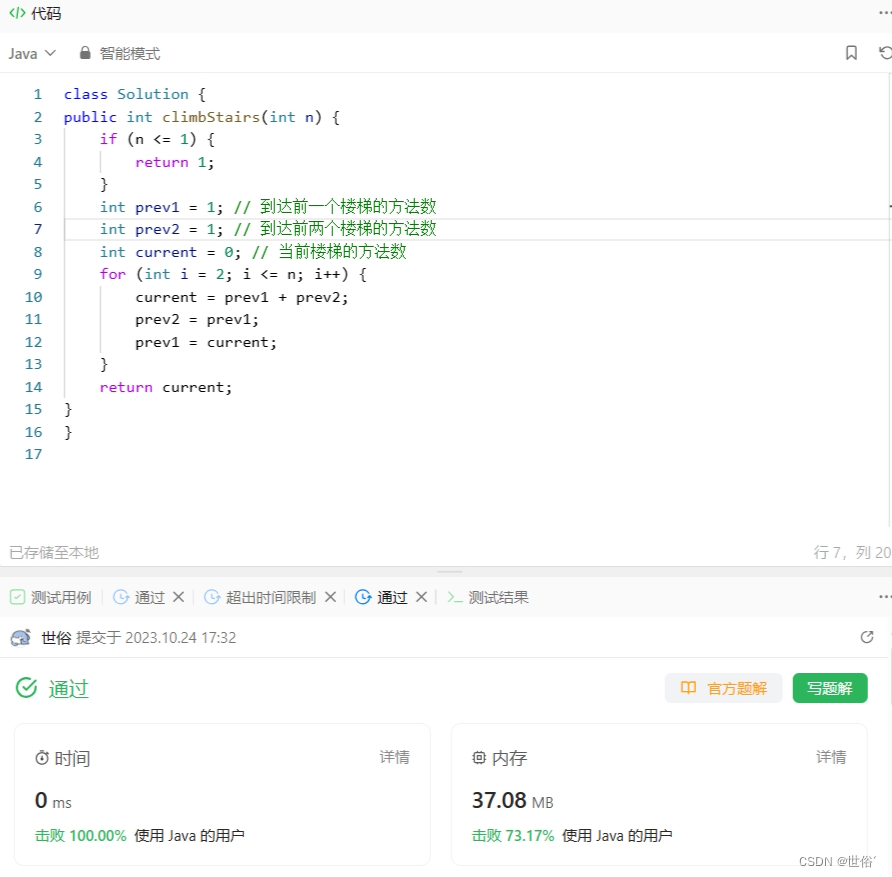
方法三:斐波那契数列公式
除了动态规划和迭代,还可以使用斐波那契数列公式的方法来解决爬楼梯问题。
斐波那契数列公式是一个通用的公式,可以用来计算斐波那契数列中任意一项的值。在爬楼梯问题中,我们可以利用斐波那契数列公式来计算到达第n阶楼梯的方法数。
具体步骤如下:
- 定义常量phi为(1 + sqrt(5)) / 2,定义常量psi为(1 - sqrt(5)) / 2。
- 利用斐波那契数列公式,计算第n+1项斐波那契数列的值,即Fn+1 = (phi^(n+1) - psi^(n+1)) / sqrt(5)。
- 最后,到达第n阶楼梯的方法数即为Fn+1。
class Solution {
public int climbStairs(int n) {double phi = (1 + Math.sqrt(5)) / 2;double psi = (1 - Math.sqrt(5)) / 2;double fn = (Math.pow(phi, n + 1) - Math.pow(psi, n + 1)) / Math.sqrt(5);return (int) Math.round(fn);
}
}
复杂度分析:
- 时间复杂度:O(1),直接使用斐波那契数列公式计算结果。
- 空间复杂度:O(1),只需要常量级的额外空间。
LeetCode运行结果:
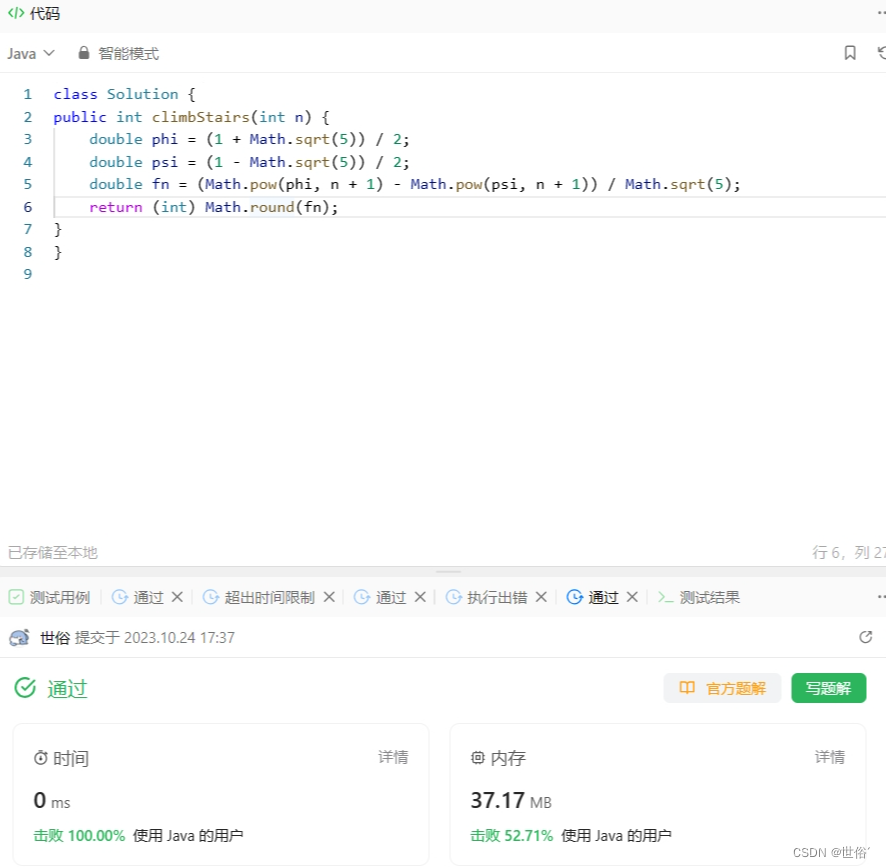
第二题
题目来源
71. 简化路径 - 力扣(LeetCode)
题目内容


解决方法
方法一:栈
class Solution {public String simplifyPath(String path) {Deque<String> stack = new LinkedList<>();String[] components = path.split("/");for (String component : components) {if (component.equals(".") || component.isEmpty()) {// 当前目录,忽略} else if (component.equals("..")) {// 上级目录,弹出栈顶元素if (!stack.isEmpty()) {stack.pop();}} else {// 其他目录,入栈stack.push(component);}}StringBuilder sb = new StringBuilder();while (!stack.isEmpty()) {sb.append("/");sb.append(stack.pollLast());}return sb.length() == 0 ? "/" : sb.toString();}
}
思路解析:
- 将路径按照"/"分割成多个组件,存储在数组components中。
- 遍历components数组,对于每个组件进行如下处理:
- 如果是"."或空字符串,表示当前目录,忽略即可。
- 如果是"..",表示上级目录,将栈顶元素弹出。
- 否则,表示其他目录,将其入栈。
- 遍历完所有组件后,将栈中元素依次弹出,拼接成简化后的路径。注意,由于栈是先进后出的,所以需要使用pollLast方法依次弹出栈顶元素。
复杂度分析:
时间复杂度分析:
- 字符串的split方法的时间复杂度为O(n),其中n是路径的长度。因为需要遍历整个路径字符串,并根据"/"进行分割。
- 遍历components数组的时间复杂度为O(m),其中m是路径中的组件数量。最坏情况下,路径中的组件数量与路径长度相等。
- 栈的操作(入栈和出栈)的时间复杂度为O(1)。
综上所述,总的时间复杂度为O(n + m)。
空间复杂度分析:
- components数组的空间复杂度为O(m),其中m是路径中的组件数量。
- 栈的空间复杂度最坏情况下为O(m),即路径中每个组件都不同。
- StringBuilder的空间复杂度为O(n),其中n是路径的长度。
综上所述,总的空间复杂度为O(n + m)。
LeetCode运行结果:
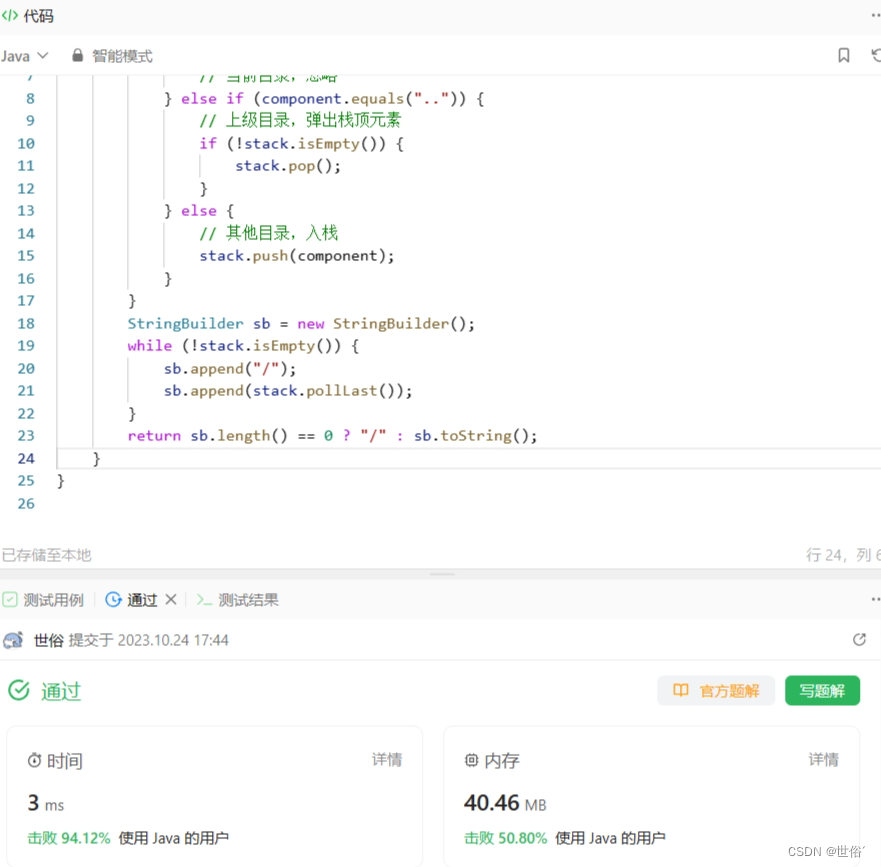
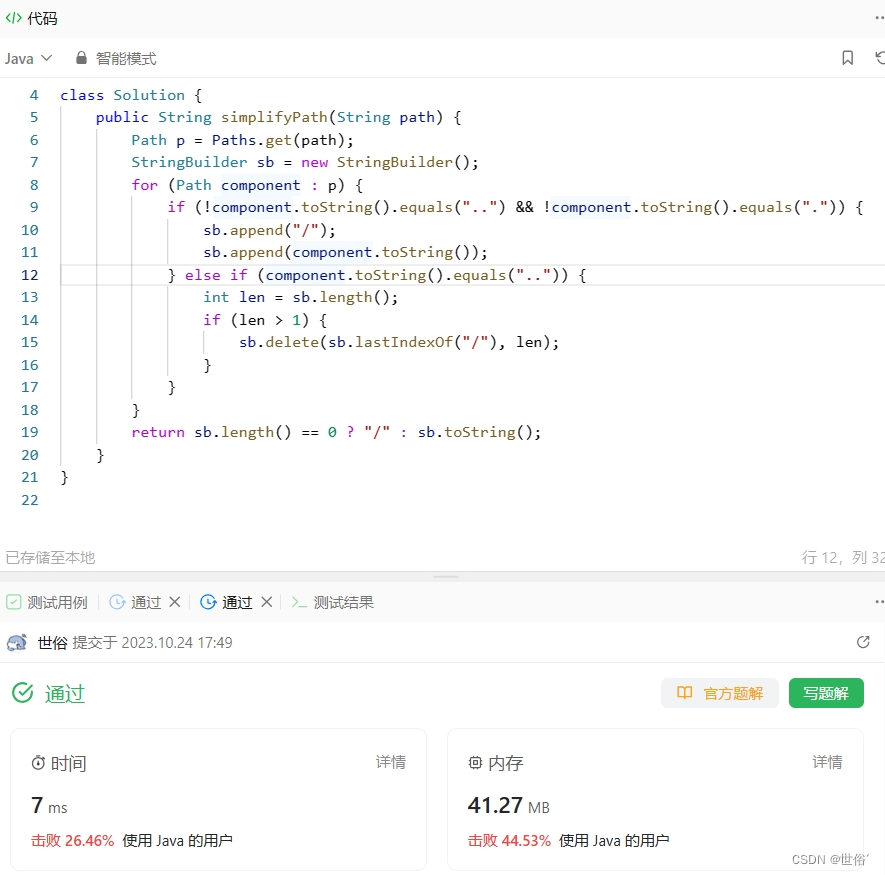
方法二:路径处理类
除了栈,还可以使用Java的路径处理类Path和Paths来实现简化路径。
思路解析:
- 使用Paths.get方法将路径字符串转换为Path对象。
- 遍历Path对象中的每个组件(即目录名或文件名)。
- 如果当前组件不是"."或"..",表示是有效的目录名或文件名,将其拼接到结果字符串中。
- 如果当前组件是"..",表示需要返回上级目录,将结果字符串中最后一个目录名删除即可。
import java.nio.file.Path;
import java.nio.file.Paths;class Solution {public String simplifyPath(String path) {Path p = Paths.get(path);StringBuilder sb = new StringBuilder();for (Path component : p) {if (!component.toString().equals("..") && !component.toString().equals(".")) {sb.append("/");sb.append(component.toString());} else if (component.toString().equals("..")) {int len = sb.length();if (len > 1) {sb.delete(sb.lastIndexOf("/"), len);}}}return sb.length() == 0 ? "/" : sb.toString();}
}
复杂度分析:
时间复杂度分析:
- Paths.get方法的时间复杂度为O(n),其中n是路径的长度。
- 遍历Path对象中的每个组件的时间复杂度为O(m),其中m是路径中的组件数量。
- StringBuilder的操作的时间复杂度为O(n),其中n是路径的长度。
综上所述,总的时间复杂度为O(n + m)。
空间复杂度分析:
- Path对象的空间复杂度为O(m),其中m是路径中的组件数量。
- StringBuilder的空间复杂度为O(n),其中n是路径的长度。
综上所述,总的空间复杂度为O(n + m)。
LeetCode运行结果:
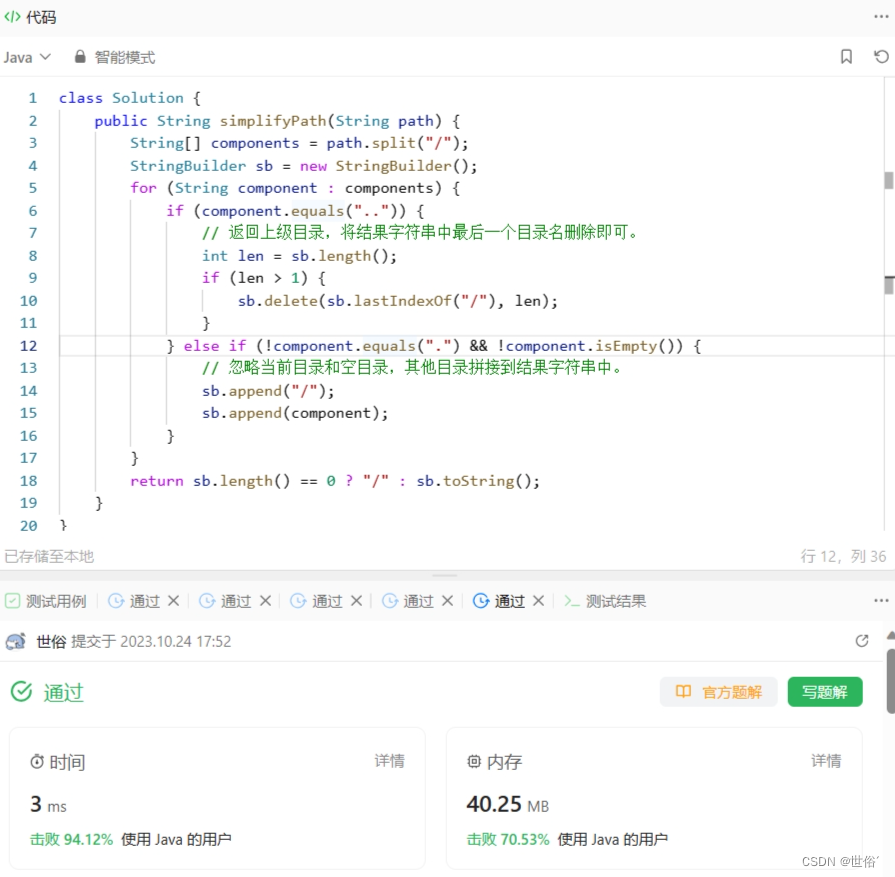
方法三:正则表达式
除了栈和Java的路径处理类,还可以使用正则表达式来实现简化路径。
思路解析:
- 将路径按照"/"分割成多个组件,存储在数组components中。
- 遍历components数组,对于每个组件进行如下处理:
- 如果是"."或空字符串,表示当前目录或空目录,忽略即可。
- 如果是"..",表示上级目录,将结果字符串中最后一个目录名删除即可。
- 否则,表示其他目录,将其拼接到结果字符串中。
- 遍历完所有组件后,返回结果字符串。注意,如果结果字符串为空,则表示路径为根目录,需要返回"/"。
class Solution {public String simplifyPath(String path) {String[] components = path.split("/");StringBuilder sb = new StringBuilder();for (String component : components) {if (component.equals("..")) {// 返回上级目录,将结果字符串中最后一个目录名删除即可。int len = sb.length();if (len > 1) {sb.delete(sb.lastIndexOf("/"), len);}} else if (!component.equals(".") && !component.isEmpty()) {// 忽略当前目录和空目录,其他目录拼接到结果字符串中。sb.append("/");sb.append(component);}}return sb.length() == 0 ? "/" : sb.toString();}
}
复杂度分析:
时间复杂度分析:
- 字符串的split方法和StringBuilder的append方法都是线性时间复杂度的,所以总时间复杂度为O(n),其中n是路径的长度。
空间复杂度分析:
- components数组的空间复杂度为O(m),其中m是路径中的组件数量。
- StringBuilder的空间复杂度为O(n),其中n是路径的长度。
综上所述,总的空间复杂度为O(n + m)。
LeetCode运行结果:
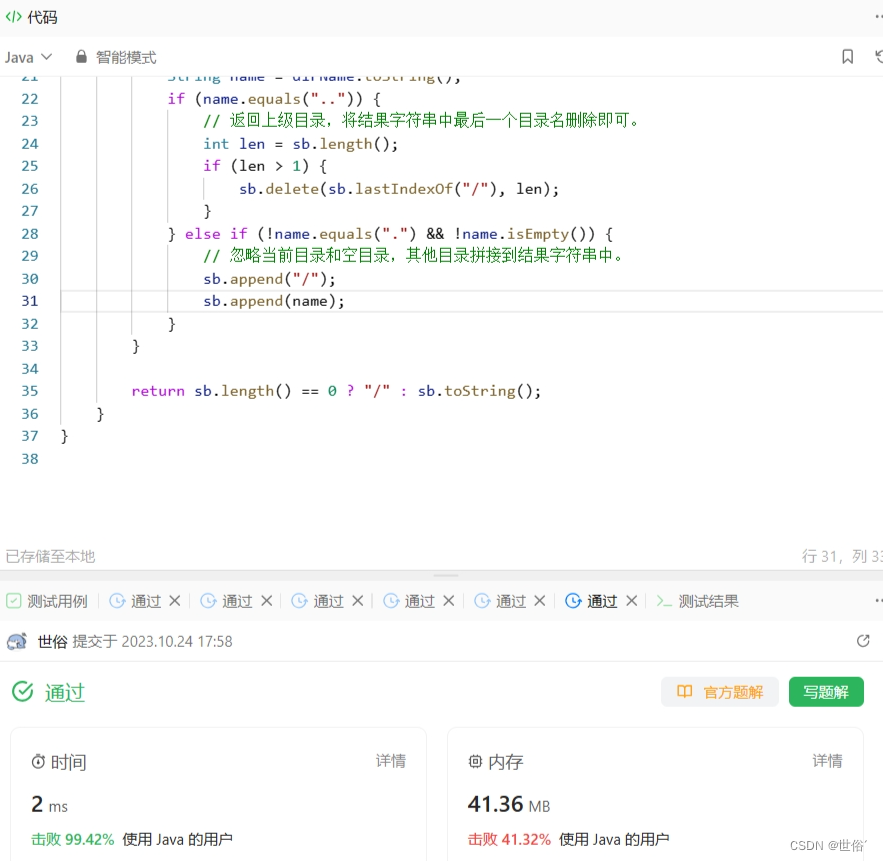
方法四:字符串处理
除了栈、Java的路径处理类、正则表达式,还可以使用字符串处理方法来实现简化路径。
思路解析:
- 使用两个指针i和j来遍历路径字符串path。
- 当指针i在路径中遇到连续的斜杠时,跳过这些多余的斜杠。
- 当指针i遇到非斜杠字符时,将其作为目录名的一部分,存储在StringBuilder对象dirName中。
- 检查dirName中的目录名:
- 如果是"."或空字符串,表示当前目录或空目录,忽略即可。
- 如果是"..",表示上级目录,将结果字符串中最后一个目录名删除即可。
- 否则,表示其他目录,将其拼接到结果字符串中。
- 继续遍历路径字符串,直到遍历完所有字符。
- 返回结果字符串。如果结果字符串为空,则表示路径为根目录,需要返回"/"。
class Solution {public String simplifyPath(String path) {StringBuilder sb = new StringBuilder();int n = path.length();int i = 0;while (i < n) {// 跳过多余的斜杠while (i < n && path.charAt(i) == '/') {i++;}// 获取当前目录名StringBuilder dirName = new StringBuilder();while (i < n && path.charAt(i) != '/') {dirName.append(path.charAt(i));i++;}// 处理当前目录名String name = dirName.toString();if (name.equals("..")) {// 返回上级目录,将结果字符串中最后一个目录名删除即可。int len = sb.length();if (len > 1) {sb.delete(sb.lastIndexOf("/"), len);}} else if (!name.equals(".") && !name.isEmpty()) {// 忽略当前目录和空目录,其他目录拼接到结果字符串中。sb.append("/");sb.append(name);}}return sb.length() == 0 ? "/" : sb.toString();}
}复杂度分析:
时间复杂度分析:
- 遍历路径字符串的过程是线性时间复杂度的,所以总时间复杂度为O(n),其中n是路径的长度。
空间复杂度分析:
- StringBuilder的空间复杂度为O(n),其中n是路径的长度。
综上所述,总的空间复杂度为O(n)。
LeetCode运行结果:
第三题
题目来源
72. 编辑距离 - 力扣(LeetCode)
题目内容

解决方法
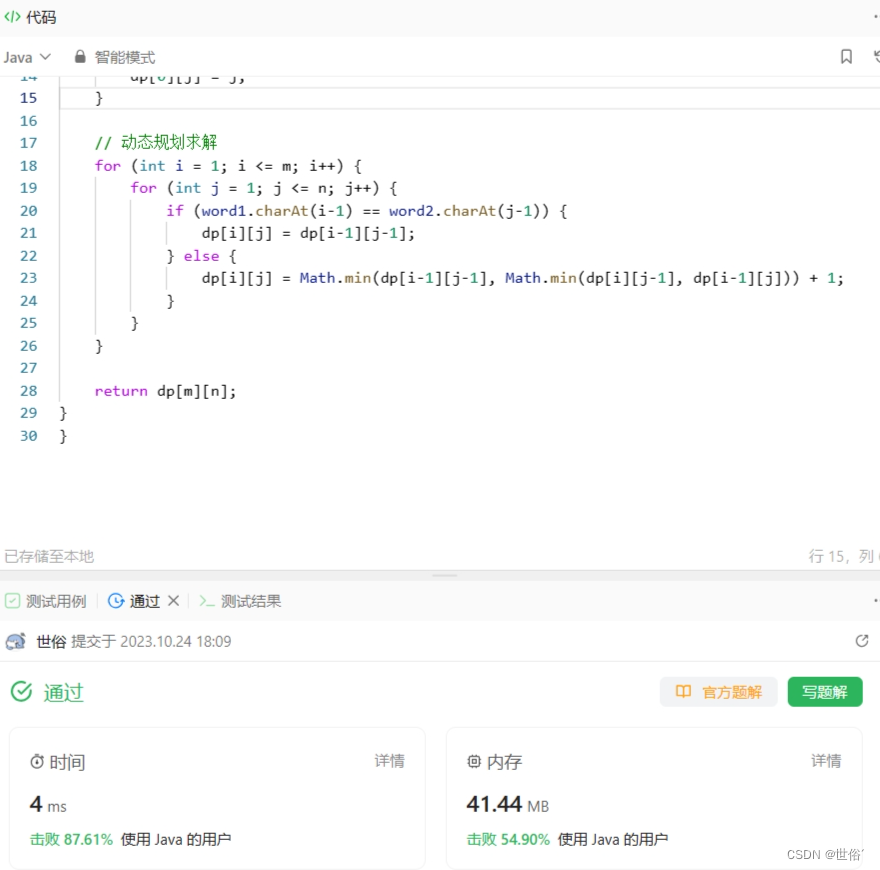
方法一:动态规划
这是一道典型的动态规划问题。
定义状态:dp[i][j]表示将word1的前i个字符转换为word2的前j个字符所需的最少操作数。
状态转移方程:
-
当word1[i] == word2[j]时,不需要进行任何操作,dp[i][j] = dp[i-1][j-1]。
-
当word1[i] != word2[j]时,可以进行三种操作:
- 插入一个字符:dp[i][j] = dp[i][j-1] + 1。
- 删除一个字符:dp[i][j] = dp[i-1][j] + 1。
- 替换一个字符:dp[i][j] = dp[i-1][j-1] + 1。
最终结果为dp[m][n],其中m和n分别是word1和word2的长度。
class Solution {
public int minDistance(String word1, String word2) {int m = word1.length();int n = word2.length();// 创建动态规划数组int[][] dp = new int[m+1][n+1];// 初始化边界条件for (int i = 0; i <= m; i++) {dp[i][0] = i;}for (int j = 0; j <= n; j++) {dp[0][j] = j;}// 动态规划求解for (int i = 1; i <= m; i++) {for (int j = 1; j <= n; j++) {if (word1.charAt(i-1) == word2.charAt(j-1)) {dp[i][j] = dp[i-1][j-1];} else {dp[i][j] = Math.min(dp[i-1][j-1], Math.min(dp[i][j-1], dp[i-1][j])) + 1;}}}return dp[m][n];
}
}复杂度分析:
该算法的时间复杂度为O(m*n),其中m和n分别是word1和word2的长度。
在动态规划求解过程中,需要填充一个大小为(m+1)(n+1)的二维数组dp。对于每个位置(i, j),都需要通过比较word1.charAt(i-1)和word2.charAt(j-1)来确定操作的类型。因此,总共需要进行mn次比较和计算。
空间复杂度方面,需要额外开辟一个大小为(m+1)(n+1)的二维数组dp来保存中间结果。因此,空间复杂度也为O(mn)。
综上所述,该算法的时间复杂度和空间复杂度均为O(m*n)。
LeetCode运行结果:
相关文章:

怒刷LeetCode的第28天(Java版)
目录 第一题 题目来源 题目内容 解决方法 方法一:动态规划 方法二:迭代 方法三:斐波那契数列公式 第二题 题目来源 题目内容 解决方法 方法一:栈 方法二:路径处理类 方法三:正则表达式 方法…...

Kotlin(八) 数据类、单例
目录 一:创建数据类 二:单例类 一:创建数据类 和Java的不同,kotlin的数据类比较简单,New→Kotlin File/Class,在弹出的对话框中输入“Book”,创建类型选择“Data”。如图: 然后编…...
IAR For ARM 安装教程
电脑环境 安装包下载 1、官网下载 ①搜索 IAR ②切换产品,选择Arm ③选择IAR Embedded Workbench for Arm ④免费试用 2、网盘下载 EWARM-CD-8202-14838.exe(访问密码: 1666) https://url48.ctfile.com/f/33868548-961057458-611638?p1666 软件下载 1、点击安…...

向量数据库Weaviate Cloud 和 Milvus Cloud:性能大比拼
最近,随着检索增强生成系统(RAG)的持续火爆,开发者对于“如何选择一个向量数据库”的疑惑也越来越多。过去几周,我们从性能和特性能力两个方面对 Weaviate Cloud 和 MilvusCloud 进行了详细的对比。在对比过程中,我们使用了开源的性能基准测试套件 VectorDBBench,围绕诸…...

微信小程序控制元素显示隐藏
微信小程序是一种轻量级的应用程序,它可以在微信中运行,具有快速、便捷、易用等特点。在微信小程序中,我们可以通过控制元素的显示和隐藏来实现特定的功能。本文将介绍如何使用微信小程序控制元素的显示和隐藏,以及如何应用这些技…...

轻量封装WebGPU渲染系统示例<2>-彩色立方体(源码)
当前示例源码github地址: https://github.com/vilyLei/voxwebgpu/blob/version-1.01/src/voxgpu/sample/VertColorCube.ts 此示例渲染系统实现的特性: 1. 用户态与系统态隔离。 2. 高频调用与低频调用隔离。 3. 面向用户的易用性封装。 4. 渲染数据和渲染机制分离。 5. …...
电脑技巧:Win10飞行模式相关知识介绍
目录 一、飞行模式简介 二、如何开关Windows 10中的飞行模式 方法一:使用硬件开关 方法二:使用Windows 10操作中心 方法三:使用Windows 10设置 三、飞行模式开关被卡住、变灰或不工作时怎么办 什么是 Windows 10 飞行模式? 用户如何打…...

化身全能战士:ChatGPT助我横扫办公室【文末送书两本】
化身全能战士:ChatGPT助我横扫办公室 半年签约 16 本书有 ChatGPT 不会的吗?解锁 ChatGPT 秘技,化身全能战士ChatGPT 基本知识办公自动化职场学习与变现 作者简介结语购买链接参与方式往期赠书回顾 🏘️🏘️个人简介&a…...

直方图均衡化算法
直方图均衡化是一种图像处理算法,通过调整图像的灰度级分布,增强图像的对比度和细节。下面是直方图均衡化算法的基本步骤: 统计原始图像的灰度直方图:遍历整个图像,计算每个灰度级出现的频次。 计算累积直方图&#x…...

通过el-tree 懒加载树,创建国家地区四级树
全国四级行政地区树数据库sql下载路径:【免费】全国四级地区(省市县)数据表sql资源-CSDN文库https://download.csdn.net/download/weixin_51722520/88469807?spm1001.2014.3001.5503 我在后台获取地区信息添加了限制,只获取parentid为当前的地…...
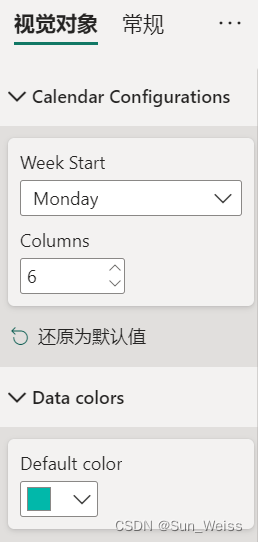
Power BI 实现日历图,在一张图中展示天、周、月数据变化规律
《数据可视化》这本书里介绍了一个时间可视化的案例(如下图所示),以日历图的形式展示数据的变化,可以在一张图上同时观察到:(1)每一天的数据变化;(2)随周变化…...

C/C++计算表达式值 2020年12月电子学会青少年软件编程(C/C++)等级考试一级真题答案解析
目录 C/C计算表达式值 一、题目要求 1、编程实现 2、输入输出 二、算法分析 三、程序编写 四、程序说明 五、运行结果 六、考点分析 C/C计算表达式值 2020年12月 C/C编程等级考试一级编程题 一、题目要求 计算(ab)*(c-b)的值 1、编程实现 给定3个整数a、b、c&…...

XTU-OJ 1258-矩阵
编写一个程序,将1~n2按行依次填入nn的矩阵,执行若干条行或者列的循环移动的指令,再将数字按行依次取出。 指令如下: 指令含义L x yx行循环左移y次R x yx行循环右移y次U x yx列循环上移y次D x yx列循环下移y次 输入 第一行是一个整…...

Django token 认证原理与实战
概述 cookie、session 与token 的区别 Cookie的作用 cookie的存储量很小,一般不超过4Kcookie并不会保存很多信息,一般用来存储登录状态cookie是以键值对进行表示的(keyvalue),例如nameli,表示cookie的名字是name,cookie携带的值是licookie的存储分为会…...
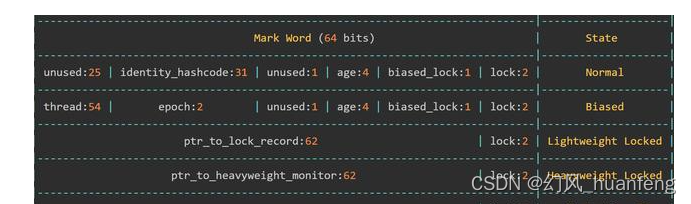
JVM虚拟机:Java对象的头信息有什么?
本文重点 在前面的课程中,我们学习了对象头,其中对象头包含Mark Word和class pointer,当然数组还会有一个数组长度。本文主要分析Mark Work中包含的信息。 Mark Word 以下两张图是一个意思: 32位 32位 64位 以上就是Mark Word会存储的信息,这个意思是说Java对象在不同…...
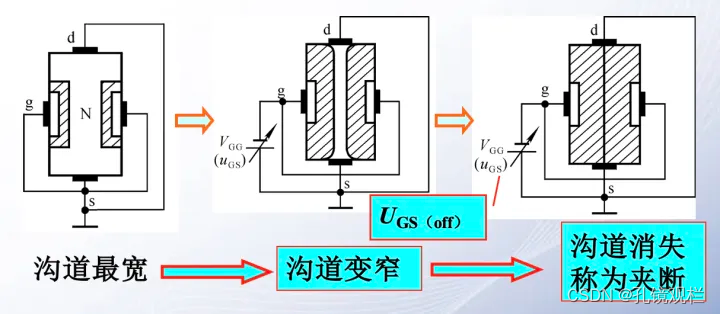
场效应管器件
在面试硬件方面的工作时,我们通常会被提问模电方面的知识。 场效应管简称FET,有三级:源极(S)、漏极(D)、栅极(G);可以实现电压控制电流源;“源极和漏极之间的漏极电流Id,由栅极的负电压进行控制…...

javascript之for循环介绍
javascript之for循环介绍 1)语法: for ([initialization]; [condition]; [final-expression]) { // code to be executed }1)initialization(初始化):在循环开始之前执行,通常用于设置循环计…...
【机器学习可解释性】3.部分依赖图
机器学习可解释性 1.模型洞察的价值2.特征重要性排列3.部分依赖图4.SHAP Value5.SHAP Value 高级使用 正文 每个特征怎么样影响预测结果? 部分依赖图 Partial Dependence Plots 虽然特征重要性显示了哪些变量对预测影响最大,但部分依赖图显示了特征如…...

在CARLA中手动开车,添加双目相机stereo camera,激光雷达Lidar
CARLA的使用逻辑: 首先创建客户端 设置如果2秒没有从服务器返回任何内容,则终止 client carla.Client("127.0.0.1", 2000) client.set_timeout(2.0) 从客户端中get world world client.get_world() 设置setting并应用 这里使用固定时…...

【VUE】ArcoDesign之自定义主题样式和命名空间
前言 Arco Design是什么? Arco Design 是由字节跳动推出的企业级产品的完整设计和开发解决方案前端组件库 官网地址:https://arco.design/同时也提供了一套开箱即用的中后台前端解决方案:Arco Design Pro(https://pro.arco.design/) Arco De…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...
