【数据结构】优先级队列
⭐ 作者:小胡_不糊涂
🌱 作者主页:小胡_不糊涂的个人主页
📀 收录专栏:浅谈数据结构
💖 持续更文,关注博主少走弯路,谢谢大家支持 💖
PriorityQueue
- 1. 什么是优先级队列
- 2. 模拟实现
- 2.1 堆
- 2.2 堆的存储方式
- 2.3 堆的创建
- 2.3.1 向下调整
- 2.3.2 堆的创建
- 2.3.3 建堆的时间复杂度
- 2.4 堆的插入与删除
- 2.4.1 插入
- 2.4.2 删除
- 3. 常用接口介绍
- 3.1 PriorityQueue的特性
- 3.2 常用接口
1. 什么是优先级队列
首先,我们知道队列是一种先进先出(FIFO)的数据结构,但有些情况下,操作的数据可能带有优先级,一般出队列时,可能需要优先级高的元素先出队列。
该中场景下,使用队列显然不合适,比如:在手机上玩游戏的时候,如果有来电,那么系统应该优先处理打进来的电话。
在这种情况下,数据结构应该提供两个最基本的操作,一个是返回最高优先级对象,一个是添加新的对象。这种数据结构就是优先级队列(Priority Queue)。
2. 模拟实现
JDK1.8中的PriorityQueue底层使用了堆这种数据结构,而堆实际就是在完全二叉树的基础上进行了一些调整。
2.1 堆
如果有一个关键码的集合K = {k0,k1, k2,…,kn-1},把它的所有元素按完全二叉树的顺序存储方式存储 在一个一维数组中,并满足:Ki <= K2i+1 且 Ki<= K2i+2 (Ki >= K2i+1 且 Ki >= K2i+2) i = 0,1,2…,则称为小堆(或大堆)。
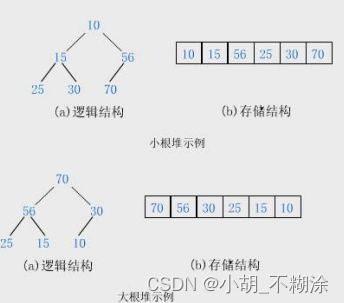
将根节点最大的堆叫做最大堆或大根堆,根节点最小的堆叫做最小堆或小根堆。
堆的性质:
- 堆中某个节点的值总是不大于或不小于其父节点的值;
- 堆总是一棵完全二叉树。
2.2 堆的存储方式
从堆的概念可知,堆是一棵完全二叉树,因此可以层序的规则采用顺序的方式来高效存储。
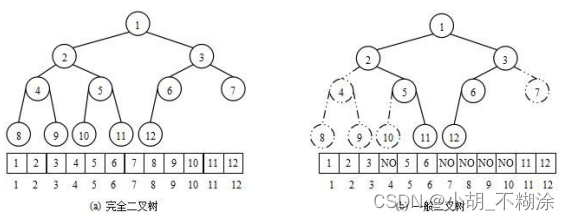
对于非完全二叉树,则不适合使用顺序方式进行存储,因为为了能够还原二叉树,空间中必须要存储空节点,就会导致空间利用率比较低。
将元素存储到数组中后,可以根据二叉树的性质对树进行还原。假设i为节点在数组中的下标,则有:
- 如果i为0,则i表示的节点为根节点,否则i节点的双亲节点为 (i - 1)/2–向下取整
- 如果2 * i + 1 小于节点个数,则节点i的左孩子下标为2 * i + 1,否则没有左孩子
- 如果2 * i + 2 小于节点个数,则节点i的右孩子下标为2 * i + 2,否则没有右孩子
2.3 堆的创建
2.3.1 向下调整
对于集合{ 27,15,19,18,28,34,65,49,25,37 }中的数据,如果将其创建成堆呢?
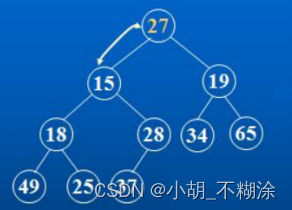
仔细观察上图后发现:根节点的左右子树已经完全满足堆的性质,因此只需将根节点向下调整好即可。
向下调整过程(以小堆为例):
- 让parent标记需要调整的节点,child标记parent的左孩子(注意:parent如果有孩子一定先是有左孩子)
- 如果parent的左孩子存在,即:child < size,进行以下操作,直到parent的左孩子不存在
- parent右孩子如果存在,找到左右孩子中最小的孩子,让child进行标记
- 将parent与较小的孩子child比较,如果:parent小于较小的孩子child,调整结束;否则:交换parent与较小的孩子child,交换完成之后,parent中大的元素向下移动,可能导致子树不满足对的性质,因此需要继续向下调整,即parent = child;child = parent*2+1;然后继续第2步。
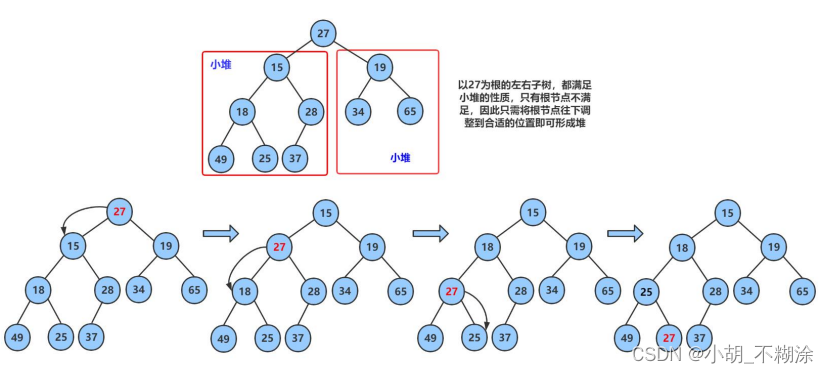
代码实现:
private void shiftDown(int parent,int len) {int child = 2*parent+1;//至少有左孩子:while (child < len) {//左孩子和右孩子比较大小,如果右孩子的值小,则那么if(child+1 < len && elem[child] > elem[child+1]) {child = child+1;}//走完上述if语句,在child下标一定保存的是左右两个孩子最小值的下标if(elem[child] < elem[parent]) {//交换swap(child,parent);parent = child;child = 2*parent+1;}else {break;}}}private void swap(int i,int j) {int tmp = elem[i];elem[i] = elem[j];elem[j] = tmp;}
在调整以parent为根的二叉树时,必须要满足parent的左子树和右子树已经是堆了才可以向下调整。
时间复杂度分析:最坏的情况即图示的情况,从根一路比较到叶子,比较的次数为完全二叉树的高度,即时间复杂度为O(log2n)。
2.3.2 堆的创建
对于普通的序列{ 1,5,3,8,7,6 },即根节点的左右子树不满足堆的特性,又该如何调整呢?
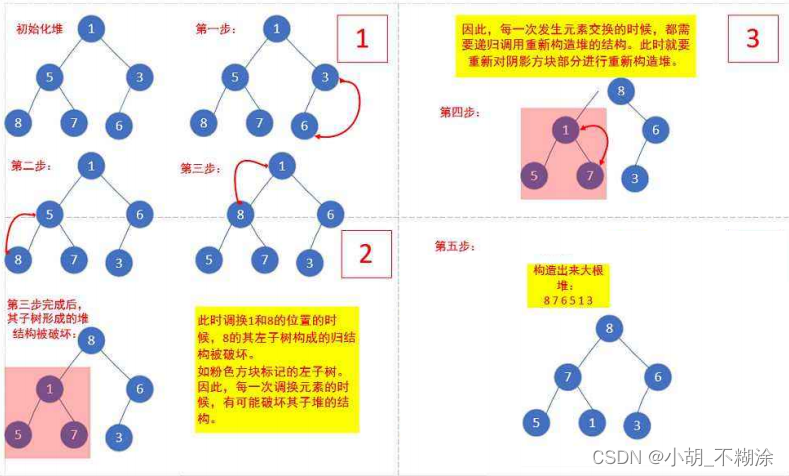
public static void createHeap(int[] array) {// 找倒数第一个非叶子节点,从该节点位置开始往前一直到根节点,遇到一个节点,应用向下调整int root = ((array.length-1-1)>>1);//int root = ((array.length-1-1)/2);for (; root >= 0; root--) {shiftDown(array, root);}
}
2.3.3 建堆的时间复杂度
因为堆是完全二叉树,而满二叉树也是完全二叉树,此处为了简化使用满二叉树来证明(时间复杂度本来看的就是近似值,多几个节点不影响最终结果):
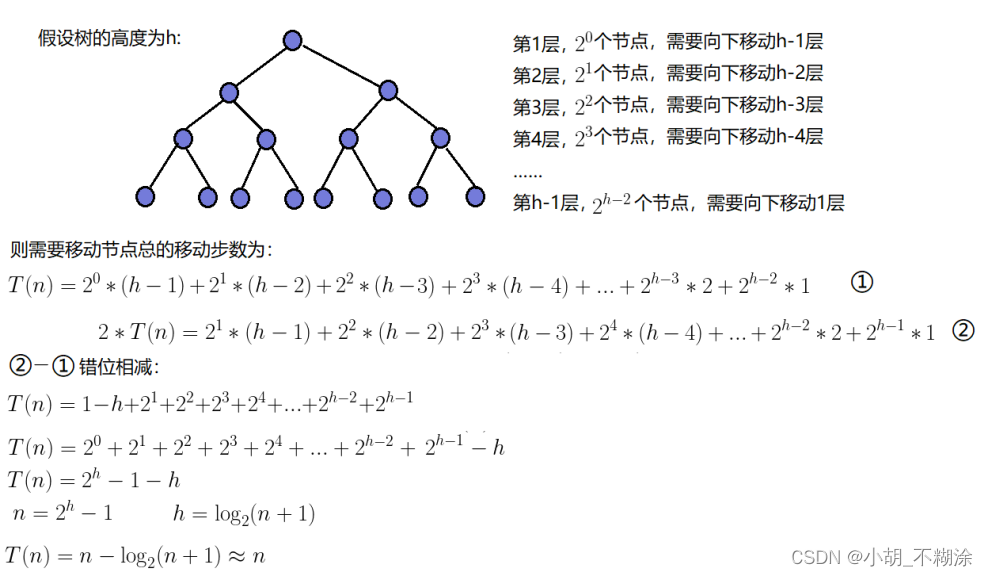
因此:建堆的时间复杂度为O(N)
2.4 堆的插入与删除
2.4.1 插入
堆的插入总共需要两个步骤:
- 先将元素放入到底层空间中(注意:空间不够时需要扩容)
- 将最后新插入的节点向上调整,直到满足堆的性质
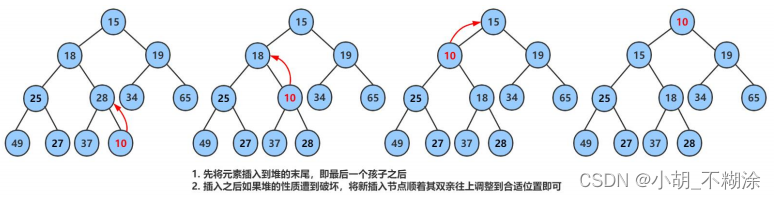
public void shiftUp(int child) {// 找到child的双亲int parent = (child - 1) / 2;while (child > 0) {// 如果双亲比孩子小,parent满足堆的性质,调整结束if (elem[parent] < elem[child]) {break;}else{// 将双亲与孩子节点进行交换int t = elem[parent];elem[parent] = elem[child];elem[child] = t;// 大的元素向下移动,可能到值子树不满足对的性质,因此需要继续向上调增child = parent;parent = (child - 1) / 2;}}}
2.4.2 删除
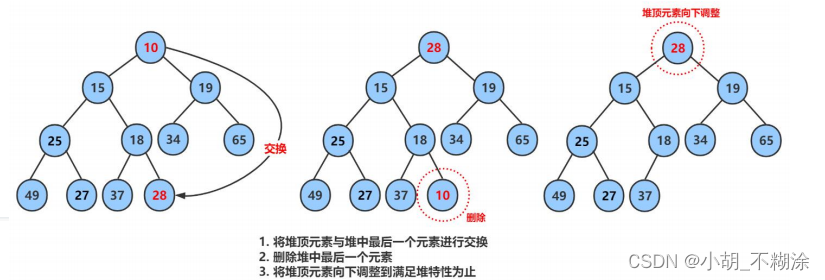
堆的删除一定删除的是堆顶元素。具体如下:
- 将堆顶元素对堆中最后一个元素交换
- 将堆中有效数据个数减少一个
- 对堆顶元素进行向下调整
3. 常用接口介绍
3.1 PriorityQueue的特性
Java集合框架中提供了PriorityQueue和PriorityBlockingQueue两种类型的优先级队列,PriorityQueue是线程不安全的,PriorityBlockingQueue是线程安全的。
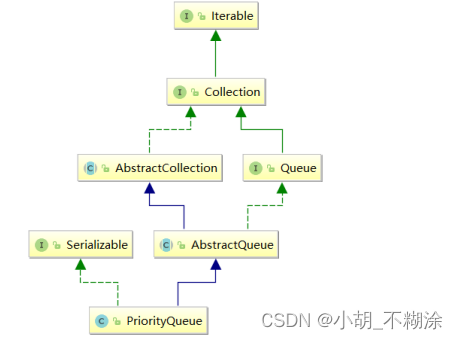
关于PriorityQueue的使用要注意:
- 使用时必须导入PriorityQueue所在的包,即:
import java.util.PriorityQueue; - PriorityQueue中放置的元素必须要能够比较大小,不能插入无法比较大小的对象,否则会抛出ClassCastException异常
- 不能插入null对象,否则会抛出NullPointerException
- 没有容量限制,可以插入任意多个元素,其内部可以自动扩容
- 插入和删除元素的时间复杂度为O(log2N)
- PriorityQueue底层使用了堆数据结构
- PriorityQueue默认情况下是小堆—即每次获取到的元素都是最小的元素
3.2 常用接口
- 优先级队列的构造
| 构造器 | 功能介绍 |
|---|---|
| PriorityQueue() | 创建一个空的优先级队列,默认容量是11 |
| PriorityQueue(intinitialCapacity) | 创建一个初始容量为initialCapacity的优先级队列,注意:initialCapacity不能小于1,否则会抛IllegalArgumentException异常 |
| PriorityQueue(Collection<?extends E> c) | 用一个集合来创建优先级队列 |
上述方法的实现:
static void TestPriorityQueue(){// 创建一个空的优先级队列,底层默认容量是11PriorityQueue<Integer> q1 = new PriorityQueue<>();// 创建一个空的优先级队列,底层的容量为initialCapacityPriorityQueue<Integer> q2 = new PriorityQueue<>(100);ArrayList<Integer> list = new ArrayList<>();list.add(4);list.add(3);list.add(2);list.add(1);// 用ArrayList对象来构造一个优先级队列的对象PriorityQueue<Integer> q3 = new PriorityQueue<>(list);System.out.println(q3.size());//4System.out.println(q3.peek());//1
}
- 插入/删除/获取优先级最高的元素
| 函数名 | 功能介绍 |
|---|---|
| boolean offer(E e) | 插入元素e,插入成功返回true,如果e对象为空,抛出NullPointerException异常,时 |
| 间复杂度:O(log2N) ,注意:空间不够时候会进行扩容 | |
| E peek() | 获取优先级最高的元素,如果优先级队列为空,返回null |
| E poll() | 移除优先级最高的元素并返回,如果优先级队列为空,返回null |
| int size() | 获取有效元素的个数 |
| void clear() | 清空 |
| boolean isEmpty() | 检测优先级队列是否为空,空返回true |
上述功能的实现:
static void TestPriorityQueue2(){int[] arr = {4,1,9,2,8,0,7,3,6,5};// 一般在创建优先级队列对象时,如果知道元素个数,建议就直接将底层容量给好// 否则在插入时需要不多的扩容// 扩容机制:开辟更大的空间,拷贝元素,这样效率会比较低PriorityQueue<Integer> q = new PriorityQueue<>(arr.length);for (int e: arr) {q.offer(e);}System.out.println(q.size()); // 打印优先级队列中有效元素个数 10System.out.println(q.peek()); // 获取优先级最高的元素 0// 从优先级队列中删除两个元素,再次获取优先级最高的元素q.poll();q.poll();System.out.println(q.size()); // 打印优先级队列中有效元素个数 8System.out.println(q.peek()); // 获取优先级最高的元素 2q.offer(0);System.out.println(q.peek()); // 获取优先级最高的元素 0// 将优先级队列中的有效元素删除掉,检测其是否为空q.clear();if(q.isEmpty()){System.out.println("优先级队列已经为空!!!");}else{System.out.println("优先级队列不为空");}
}
PriorityQueue的扩容方式:
private static final int MAX_ARRAY_SIZE = Integer.MAX_VALUE - 8;
private void grow(int minCapacity) {int oldCapacity = queue.length;// Double size if small; else grow by 50%int newCapacity = oldCapacity + ((oldCapacity < 64) ?(oldCapacity + 2) :(oldCapacity >> 1));// overflow-conscious codeif (newCapacity - MAX_ARRAY_SIZE > 0)newCapacity = hugeCapacity(minCapacity);queue = Arrays.copyOf(queue, newCapacity);
}
private static int hugeCapacity(int minCapacity) {if (minCapacity < 0) // overflowthrow new OutOfMemoryError();return (minCapacity > MAX_ARRAY_SIZE) ?Integer.MAX_VALUE :MAX_ARRAY_SIZE;
}
优先级队列的扩容说明:
- 如果容量小于64时,是按照oldCapacity的2倍方式扩容的
- 如果容量大于等于64,是按照oldCapacity的1.5倍方式扩容的
- 如果容量超过MAX_ARRAY_SIZE,按照MAX_ARRAY_SIZE来进行扩容
相关文章:

【数据结构】优先级队列
⭐ 作者:小胡_不糊涂 🌱 作者主页:小胡_不糊涂的个人主页 📀 收录专栏:浅谈数据结构 💖 持续更文,关注博主少走弯路,谢谢大家支持 💖 PriorityQueue 1. 什么是优先级队列…...

c语言宏相关高级用法
outline all可变参数宏c语言内置函数1.__typeof__2.__builtin_choose_expr all 记录一些c语言宏相关的高级用法 可变参数宏 c语言内置函数 1.typeof 2.__builtin_choose_expr 语法格式 type __builtin_choose_expr (const_exp, exp1, exp2)解释 这个函数的第一个参数必须…...
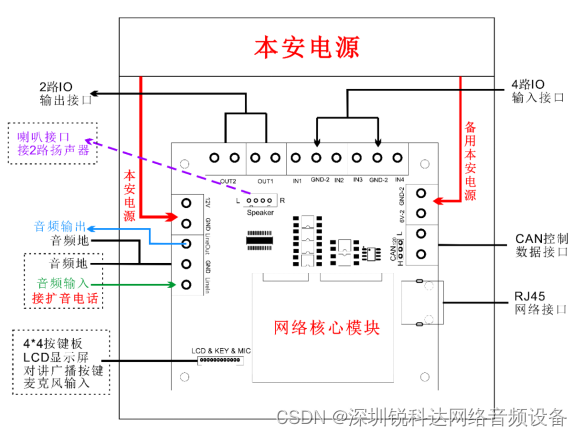
新款模块上线实现SIP模块与扩拨电话之间打点与喊话功能 IP矿用电话模块SV-2800VP
新款模块上线实现SIP模块与扩拨电话之间打点与喊话功能 IP矿用电话模块SV-2800VP 一、简介 SV-2800VP系列模块是我司设计研发的一款用于井下的矿用IP音频传输模块,可用此模块打造一套低延迟、高效率、高灵活和多扩展的IP矿用广播对讲系统,亦可对传统煤…...
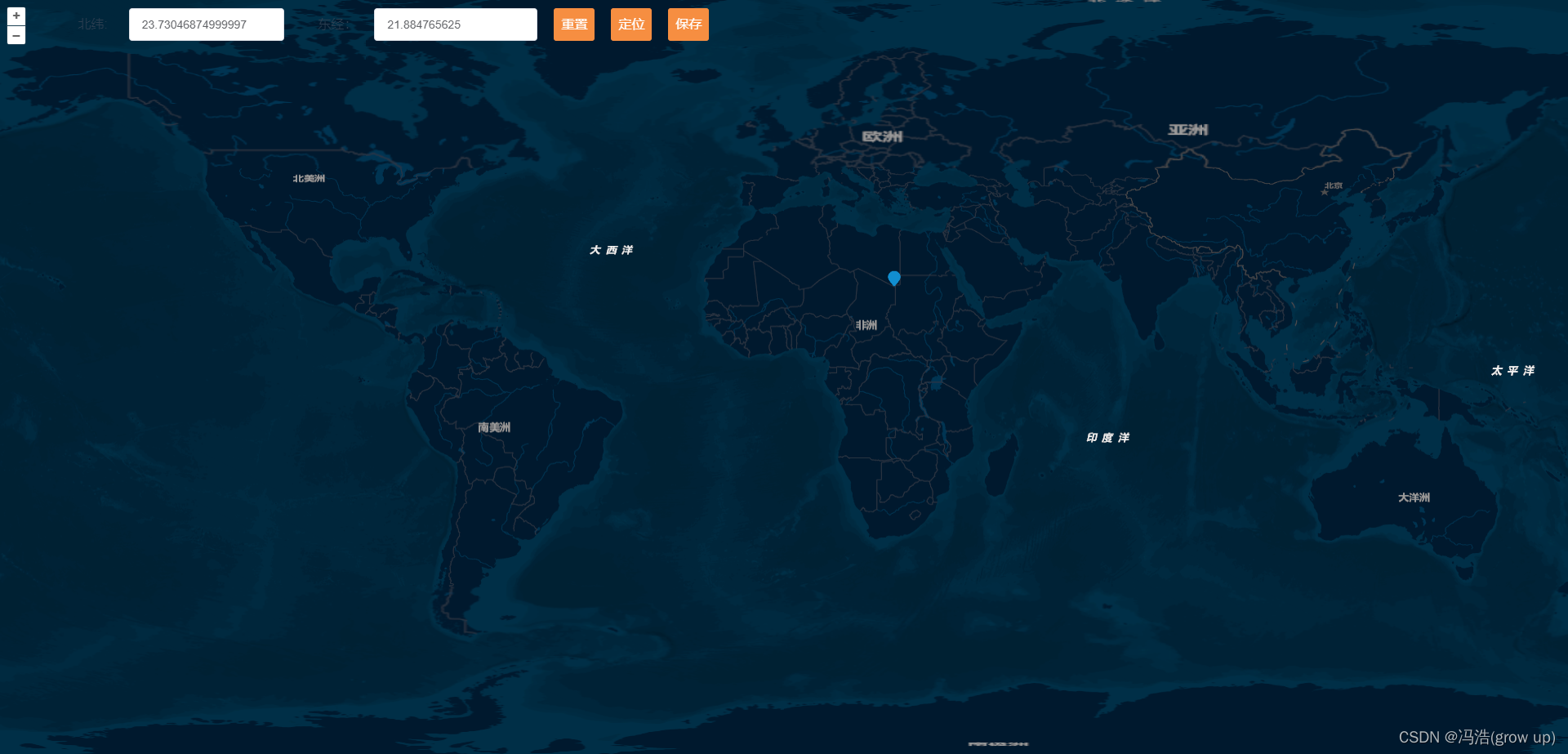
前端开发---在vue项目中使用openLayers
前端开发之在vue项目中使用openLayers 前言效果图在vue中渲染地图安装ol插件1、调用插件2、 初始话地图3、地图点击事件4、重置坐标5、通过坐标改变视图6、保存坐标点 vue中使用的源码 前言 本篇文章主要讲解openLayers的初步使用,包括渲染地图、获取点坐标、标记点…...

C语言之结构体和共用体详解
目录 结构体 结构体的定义和使用 结构体数组的使用 结构体指针的使用 结构体大小的计算 共用体 共用体的定义和使用 typedef用法详解 enum枚举类型 结构体 结构体的定义和使用 C语言的结构体(Struct)是一种自定义的数据类型,它允许…...

iOS插件
把平时看到或项目用到的一些插件进行整理,文章后面分享一些不错的实例,若你有其它的插件欢迎分享,不断的进行更新; 一:第三方插件 1:基于响应式编程思想的oc 地址:https://github.com/ReactiveCocoa/Rea…...

Maven第四章:配置文件详解
Maven第四章:配置文件详解 前言 本章重点知识:掌握setting.xml配置文件以及pom.xml配置文件 setting.xml配置文件 setting.xml文件用于配置Maven的运行环境,包括本地仓库的位置、镜像仓库的配置、认证信息等。以下是setting.xml文件的详细说明: 文件位置: 全局配置文件:…...
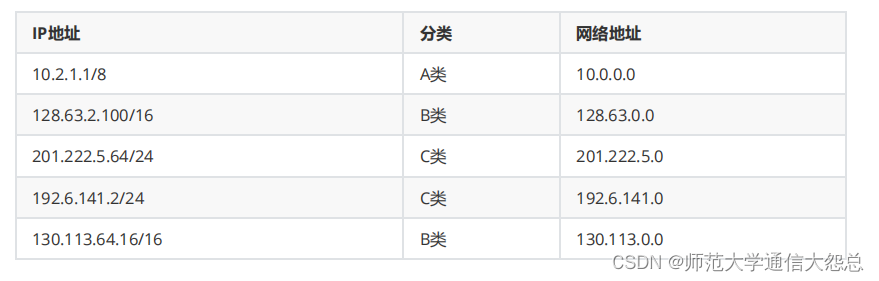
计算机网络基础一
任务背景 由于某些原因,某公司搬迁至新地方,现需要对公司网络环境重新调整规划,申请了一个 B 类 IP 地址 : 172.25.0.0 ,子 网掩码为 255.255.224.0 。需要根据公司部门和电脑数进行子网划分并分配 IP 。公司目前有 6 个部门&am…...

搜维尔科技:Touch触觉式力反馈设备与Touch X力反馈设备对比分析
此2款力反馈为最常用的力反馈设备...

SAP保持系统长时间在线
保持系统长时间在线 保持SAP系统长长时间在线不掉线,通过代码,保持一个页面一直在线,ABAP代码如下: *&---------------------------------------------------------------------* *& Report ZGUI *&----------------------------…...

威联通NAS进阶玩法之使用Docker搭建个人博客教程
Hello大家好,本篇教程主要教大家在威联通的NAS上搭建属于自己的个人博客网站,首先介绍一下我使用的机器,四盘位威联通TS-464C2,搭载四核四线程的N5095处理器,支持4K60帧的输出以及PCIE3.0,可玩性还是非常高的。废话不多…...
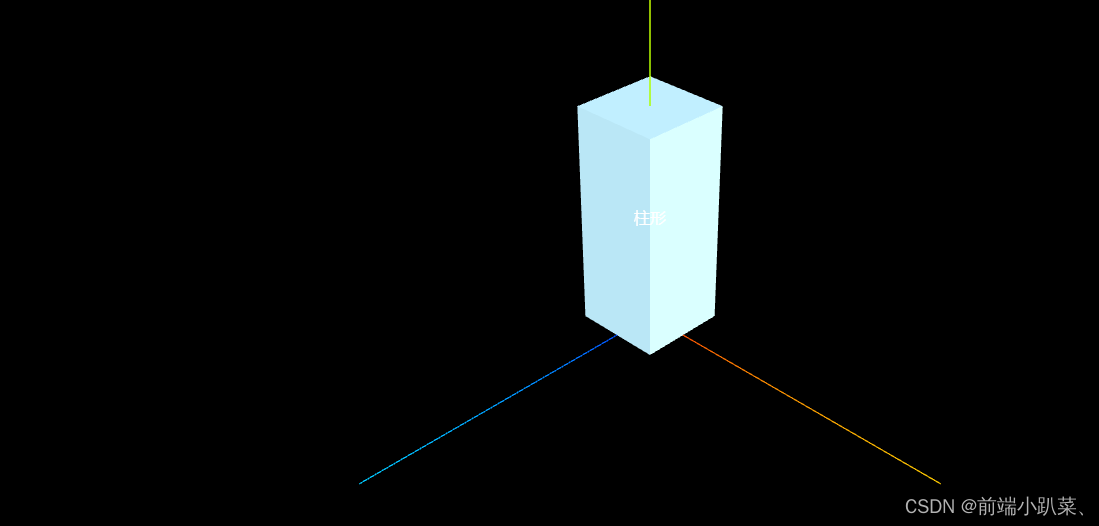
模型对象CSS2DObject始终在画布的左上角(问题解决)
写了个简单案例模拟一下这个问题,看下图片 下面看下c2渲染器相关代码部分 this.css2DRenderer new CSS2DRenderer(); this.css2DRenderer.render(this.scene, this.camera); this.css2DRenderer.setSize(width, height); this.css2DRenderer.domElement.style.pos…...
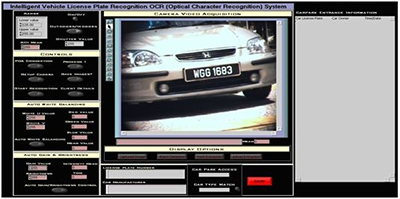
LabVIEW开发基于图像处理的车牌检测系统
LabVIEW开发基于图像处理的车牌检测系统 自动车牌识别的一般步骤是图像采集、去除噪声的预处理、车牌定位、字符分割和字符识别。结果主要取决于所采集图像的质量。在不同照明条件下获得的图像具有不同的结果。在要使用的预处理技术中,必须将彩色图像转换为灰度&am…...
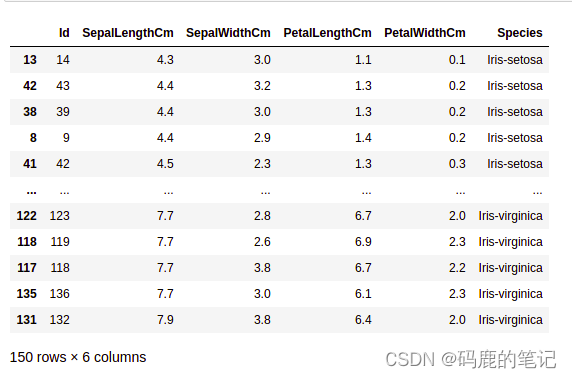
Data Analysis With Python
文章目录 Data Analysis With PythonAnalyzing Numerical Data with NumPyCreating NumPy ArrayNumPy Array SlicingNumPy Array BroadcastingAnalyzing Data Using Pandas In this article, we will discuss how to do data analysis with Python. We will discuss all sorts …...
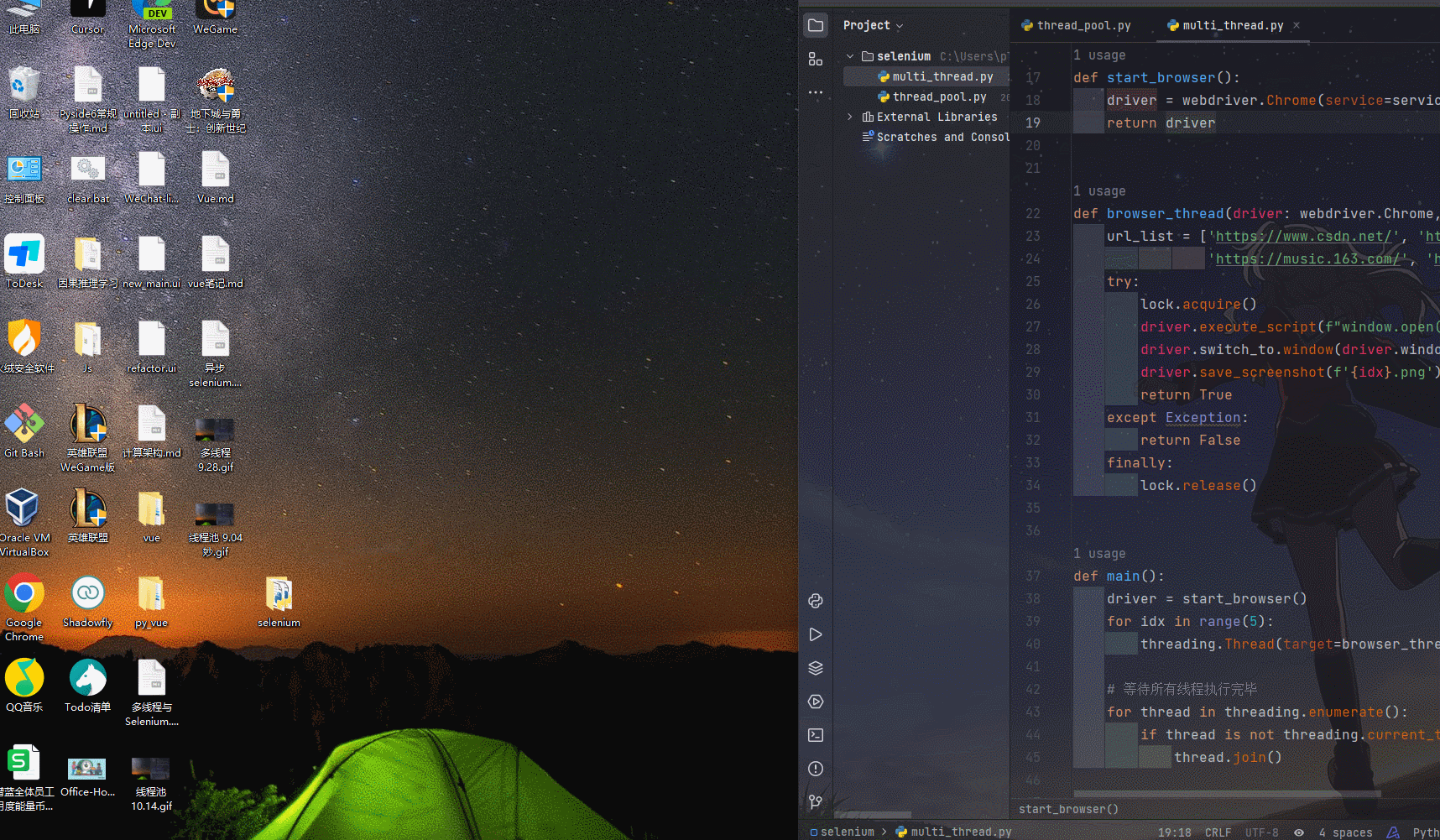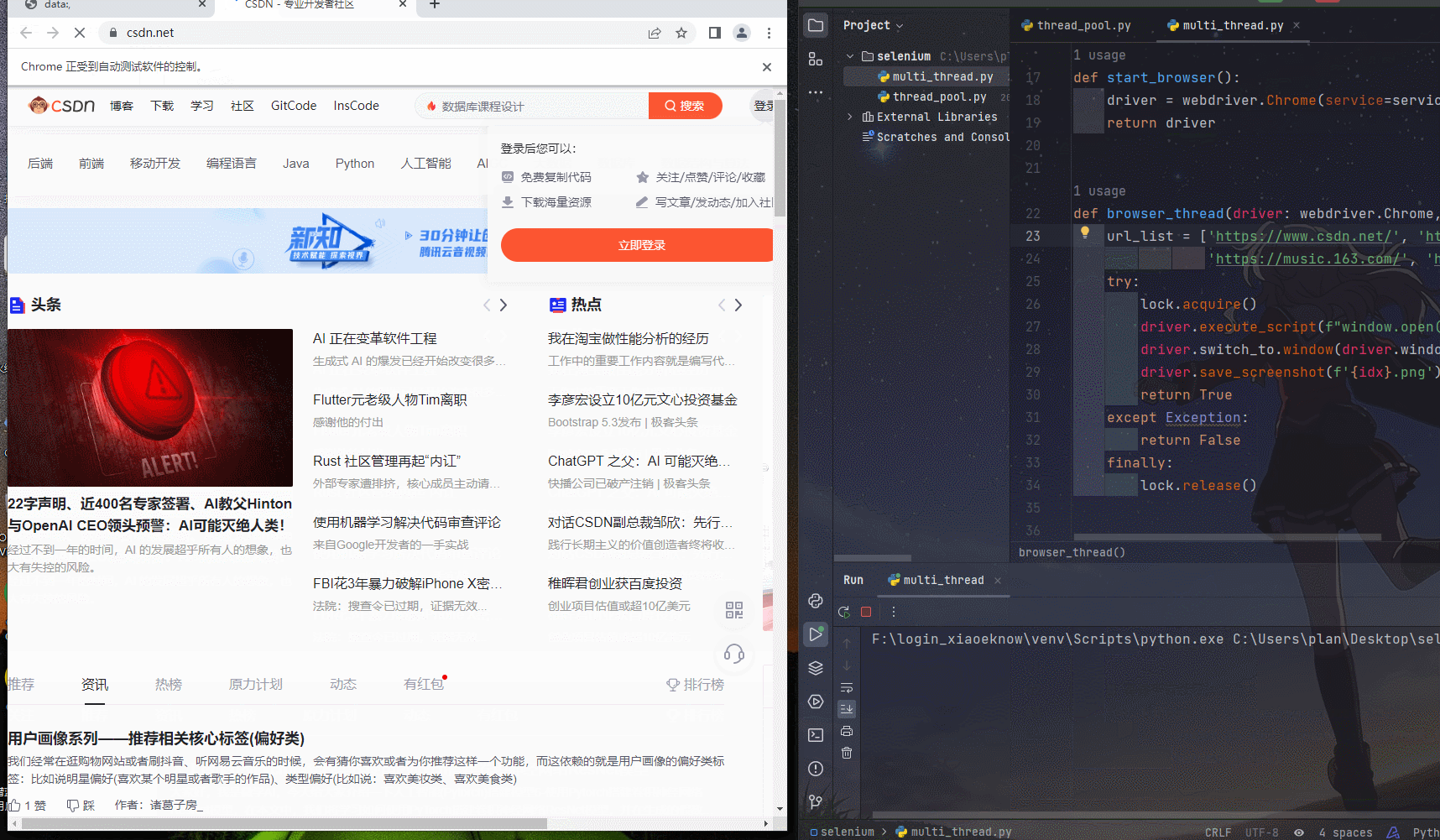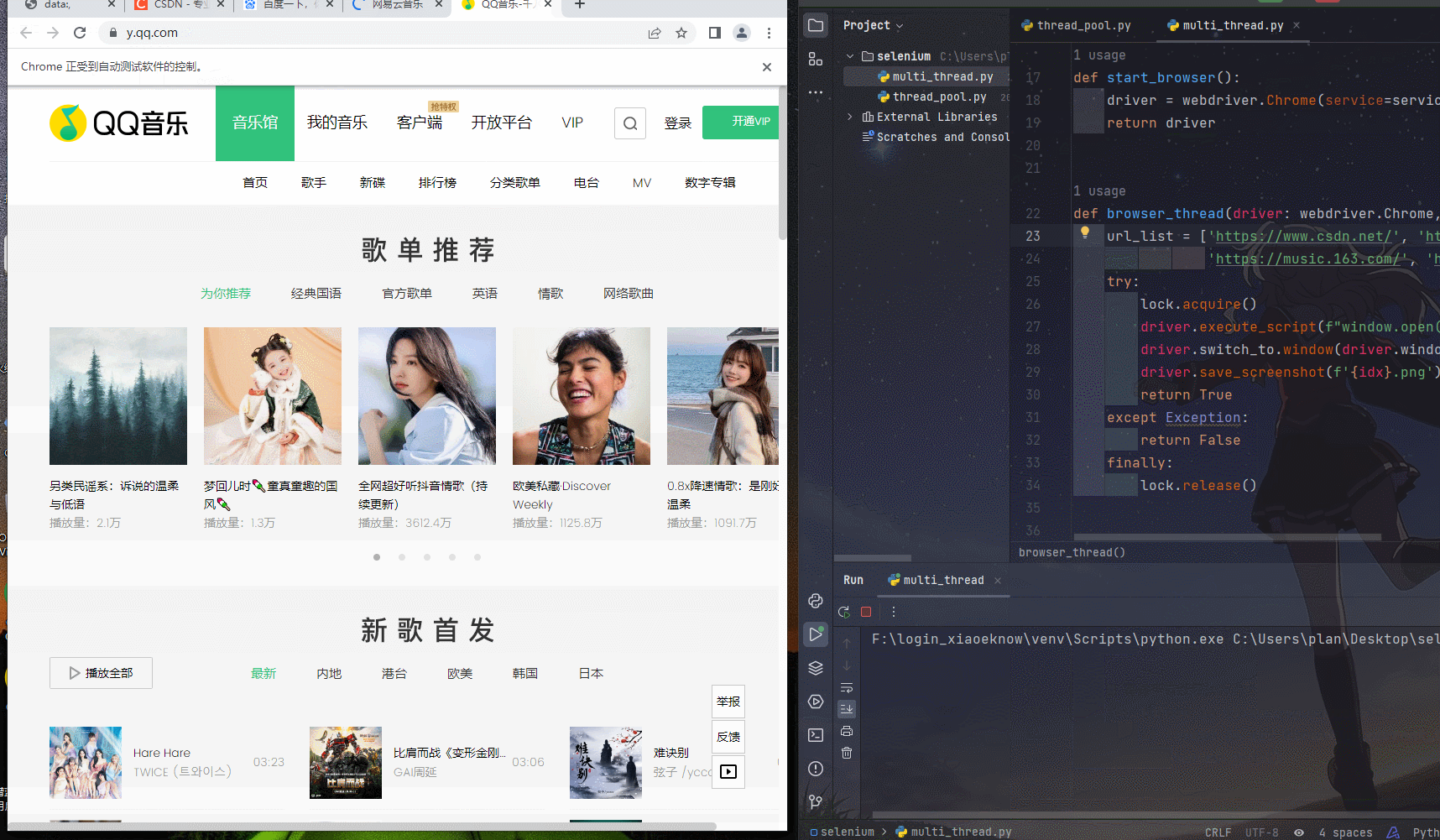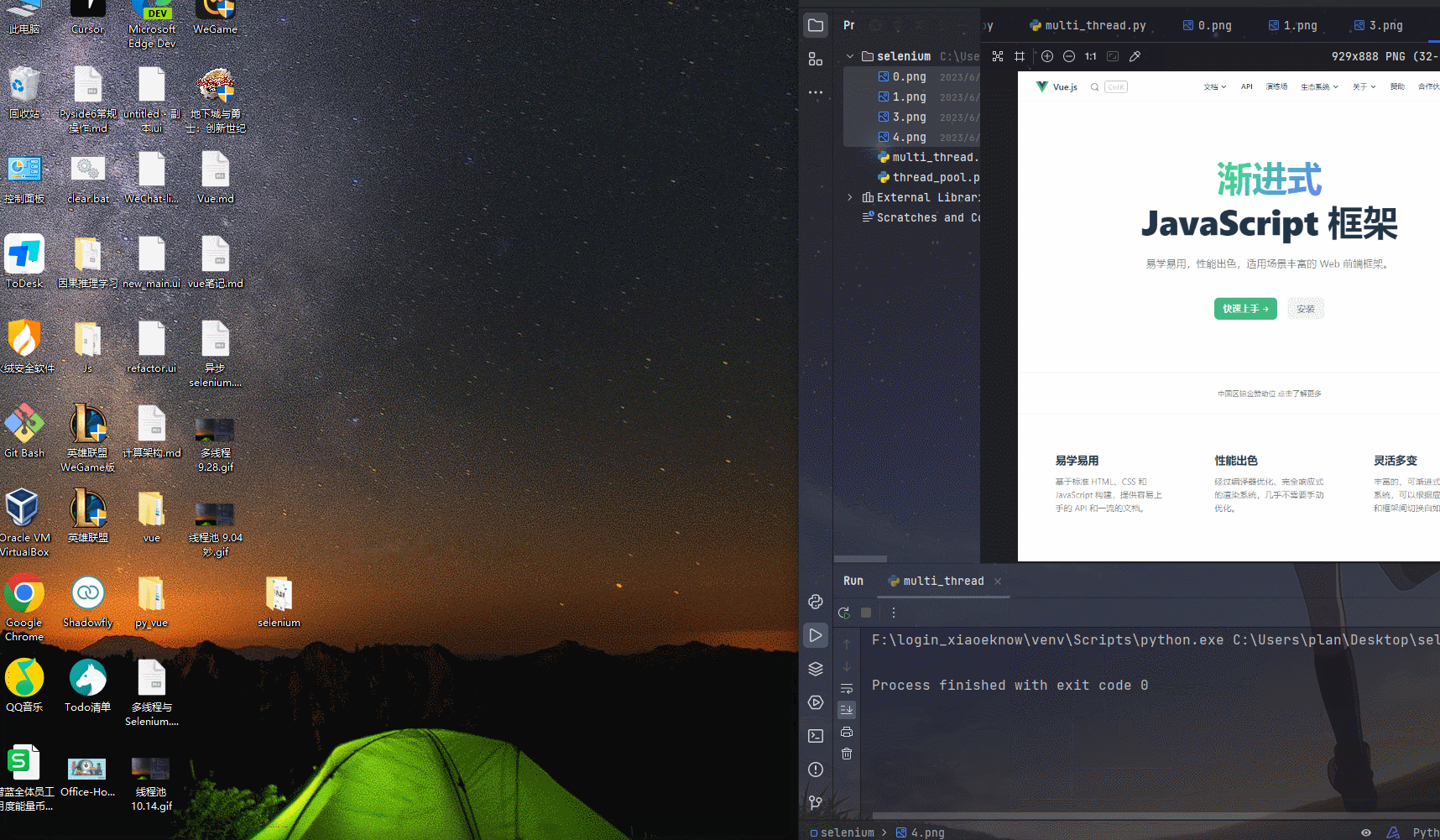
【Selenium】提高测试爬虫效率:Selenium与多线程的完美结合
前言 使用Selenium 创建多个浏览器,这在自动化操作中非常常见。 而在Python中,使用 Selenium threading 或 Selenium ThreadPoolExecutor 都是很好的实现方法。 应用场景: 创建多个浏览器用于测试或者数据采集;使用Selenium 控…...

ElCLib类解析
OpenCascade 中的 ElCLib 类提供了对基本曲线(例如 2D 和 3D 空间中的二次曲线和直线)进行基本几何计算的函数。它提供与参数化、点评估和曲线参数范围内的定位相关的各种操作和计算。以下是一些需要注意的要点: 点和矢量计算:ElC…...
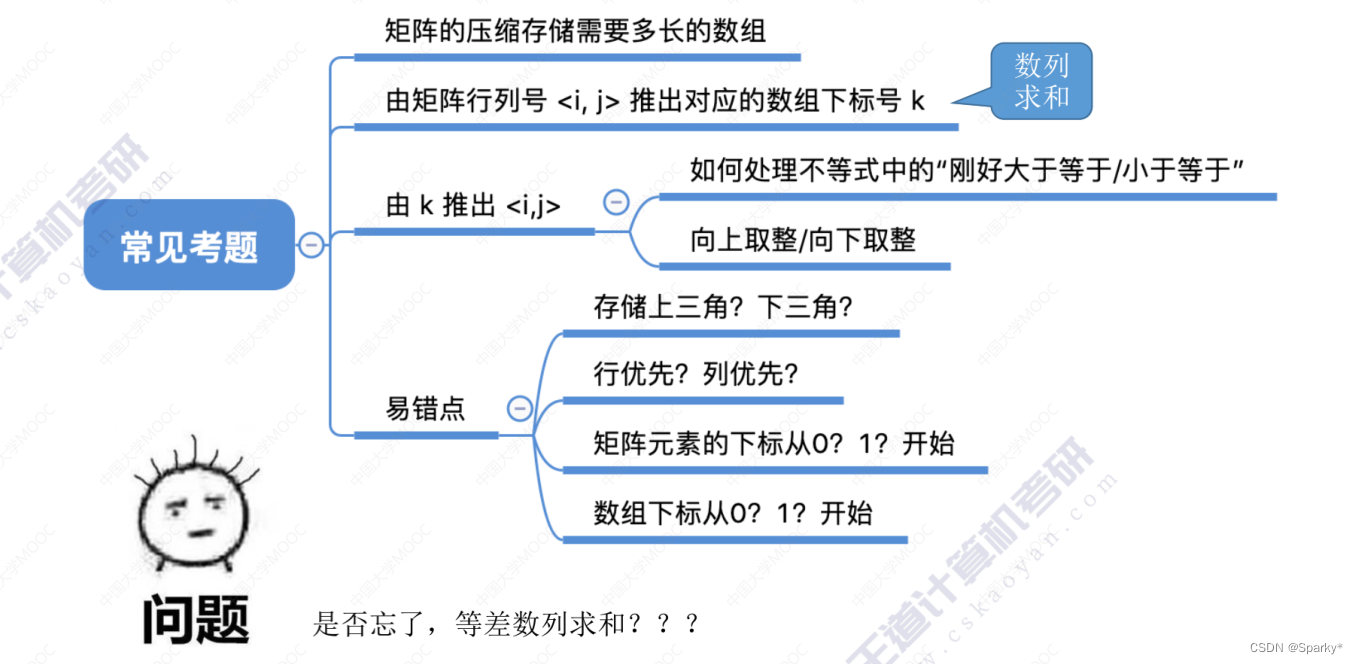
栈、队列、矩阵的总结
栈的应用 括号匹配 表达式求值(中缀,后缀) 中缀转后缀(机算) 中缀机算 后缀机算 总结 特殊矩阵 对称矩阵的压缩存储 三角矩阵 三对角矩阵 稀疏矩阵的压缩存储...
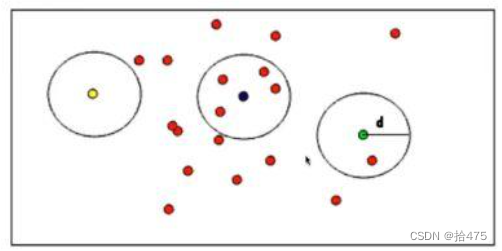
PCL 半径滤波剔除噪点
目录 一、算法原理二、注意事项三、代码实现一、算法原理 PCL半径滤波是删除在输入的点云一定范围内没有达到足够多领域的所有数据点。通俗的讲:就是以一个点p给定一个范围r,领域点要求的个数为m,r若在这个点的r范围内部的个数大于m则保留,小于m则删除。因此,使用该算法时…...
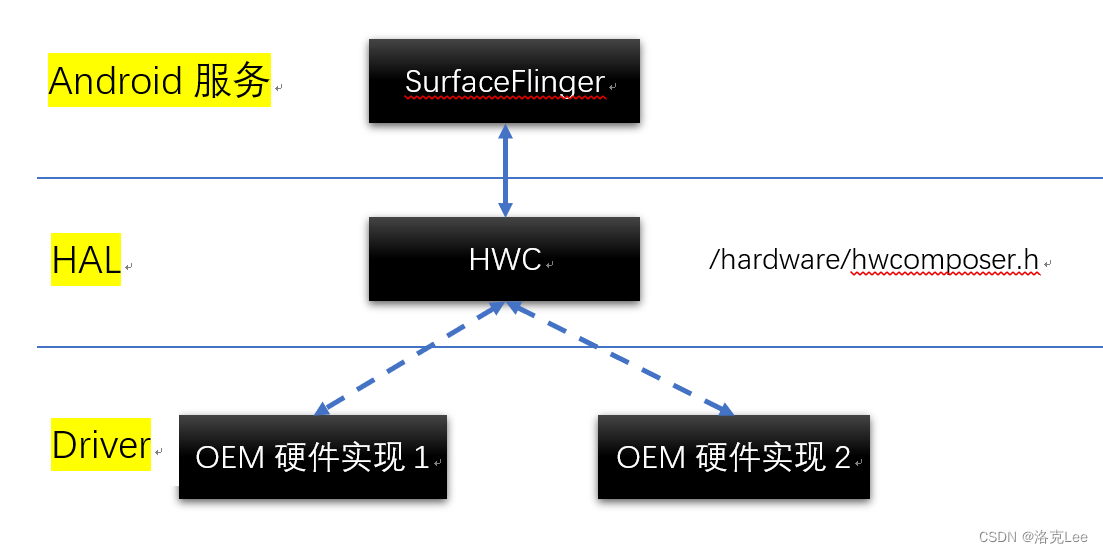
Android SurfaceFlinger做Layer合成时,如何与HAL层进行交互
目录 零、本文讨论问题的范围一、问题:SurfaceFlinger图层合成选择实现方式的两难1.1 从OpenGL ES、HWC本身来讲1.2 以HWC为主导的判断逻辑 二、SurfaceFlinger与HAL层进行交互的具体实现框架2.1 SurfaceFlinger 调用 OpenGL ES 流程2.2 FrameBuffer2.3 SurfaceFlin…...
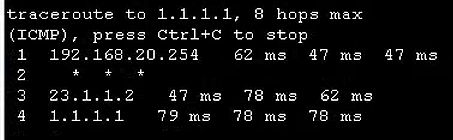
华为eNSP配置专题-策略路由的配置
文章目录 华为eNSP配置专题-策略路由的配置0、概要介绍1、前置环境1.1、宿主机1.2、eNSP模拟器 2、基本环境搭建2.1、终端构成和连接2.2、终端的基本配置 3、配置接入交换机上的VLAN4、配置核心交换机为网关和DHCP服务器5、配置核心交换机和出口路由器互通6、配置PC和出口路由器…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...

基于Java+MySQL实现(GUI)客户管理系统
客户资料管理系统的设计与实现 第一章 需求分析 1.1 需求总体介绍 本项目为了方便维护客户信息为了方便维护客户信息,对客户进行统一管理,可以把所有客户信息录入系统,进行维护和统计功能。可通过文件的方式保存相关录入数据,对…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...

【学习笔记】erase 删除顺序迭代器后迭代器失效的解决方案
目录 使用 erase 返回值继续迭代使用索引进行遍历 我们知道类似 vector 的顺序迭代器被删除后,迭代器会失效,因为顺序迭代器在内存中是连续存储的,元素删除后,后续元素会前移。 但一些场景中,我们又需要在执行删除操作…...

stm32wle5 lpuart DMA数据不接收
配置波特率9600时,需要使用外部低速晶振...

API网关Kong的鉴权与限流:高并发场景下的核心实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 引言 在微服务架构中,API网关承担着流量调度、安全防护和协议转换的核心职责。作为云原生时代的代表性网关,Kong凭借其插件化架构…...

字符串哈希+KMP
P10468 兔子与兔子 #include<bits/stdc.h> using namespace std; typedef unsigned long long ull; const int N 1000010; ull a[N], pw[N]; int n; ull gethash(int l, int r){return a[r] - a[l - 1] * pw[r - l 1]; } signed main(){ios::sync_with_stdio(false), …...