基于回溯搜索算法的无人机航迹规划-附代码
基于回溯搜索算法的无人机航迹规划
文章目录
- 基于回溯搜索算法的无人机航迹规划
- 1.回溯搜索搜索算法
- 2.无人机飞行环境建模
- 3.无人机航迹规划建模
- 4.实验结果
- 4.1地图创建
- 4.2 航迹规划
- 5.参考文献
- 6.Matlab代码
摘要:本文主要介绍利用回溯搜索算法来优化无人机航迹规划。
1.回溯搜索搜索算法
回溯搜索算法原理请参考:https://blog.csdn.net/u011835903/article/details/108366901
2.无人机飞行环境建模
? 环境模型的建立是考验无人机是否可以圆满完成人类所赋予各项任务的基
础和前提,其中第一步便是如何描述规划空间中的障碍物。首先我们将采取函数模拟法模拟地貌特征。其函数表达式为:
z ( x , y ) = s i n ( y + a ) + b s i n ( x ) + c c o s ( d y 2 + x 2 ) + e c o s ( y ) + f s i n ( f y 2 + x 2 ) + g c o s ( y ) (1) z(x,y)=sin(y+a)+bsin(x)+ccos(d\sqrt{y^2+x^2})+ecos(y)+fsin(f\sqrt{y^2+x^2})+gcos(y)\tag{1} z(x,y)=sin(y+a)+bsin(x)+ccos(dy2+x2)+ecos(y)+fsin(fy2+x2)+gcos(y)(1)
其中, ( x , y ) (x, y) (x,y) 为地形上某点投影在水平面上的点坐标, z z z 则为对应点坐标的高度。式中 a , b , c , d , e , f , g a, b, c, d, e, f , g a,b,c,d,e,f,g 是常系数,想要得到不同的地貌特征可以通过改变其常系数的大小,以上建模是作为环境模型的基准地形信息。但为了得到障碍区域我们还需要在这个基准地形上叠加山峰模型,这样就可以模拟像山峰、丘陵等障碍地理信息。山峰模型的数学表达式为:
h ( x , y ) = ∑ i h i e x p [ − ( x − x o i ) 2 a i 2 − ( y − y o i ) 2 b i 2 ] + h o (2) h(x,y)=\sum_ih_iexp[-\frac{(x-x_{oi})^2}{a_i^2}-\frac{(y-y_{oi})^2}{b_i^2}]+h_o \tag{2} h(x,y)=i∑hiexp[−ai2(x−xoi)2−bi2(y−yoi)2]+ho(2)
式 (2)中, h o h_o ho 和 h i h_i hi 分别表示基准地形和第 i i i座山峰的高度, ( x o i , y o i ) (xoi , y oi ) (xoi,yoi)则表示第 i座山峰的中心坐标位置,a i 和 b i 分别是第 i 座山峰沿 x 轴和 y 轴方向的坡度。由式(1)和(2),我们可以得到如下表达式:
Z ( x , y ) = m a x [ z ( x , y ) , h ( x , y ) ] (3) Z(x,y)=max[z(x,y),h(x,y)]\tag{3} Z(x,y)=max[z(x,y),h(x,y)](3)
无人机在躲避障碍物的同时也会经常遇到具有威胁飞行安全的区域,我们称之为威胁区域。这些威胁区域可以是敌人的雷达和防空导弹系统的探测威胁区域也可以是一些其它的威胁,一旦无人机进入这些区域很有可能会被击落或者坠毁。为了简化模型,本文采用半径为 r 的圆柱形区域表示威胁区域,其半径的大小决定威胁区域的覆盖范围。每一个圆柱体的中心位置是对无人机构成最大威胁的地方并向外依次减弱。
3.无人机航迹规划建模
? 在环境建模的基础上,无人机航迹规划需要考虑到在执行复杂任务的过程中自身性能约束要求,合理的设计航迹评价函数才能使得回溯搜索搜索算法得出的最后结果符合要求,并保证规划出的航迹是有效的。考虑到实际环境中,无人机需要不断适应变化的环境。所以在无人机路径规划过程中,最优路径会显得比较复杂,并包含许多不同的特征。基于实际的情况,本文采用较为复杂的航迹评价函数进行无人机路径规划。影响无人机性能的指标主要包括航迹长度、飞行高度、最小步长、转角代价、最大爬升角等。
? 搜索最佳路径通常与搜索最短路径是密不可分的。在无人机航迹规划过程中,航迹的长度对于大多数航迹规划任务来说也是非常重要的。众所周知,较短的路线可以节省更多的燃料和更多的时间并且发现未知威胁的几率会更低。我们一般把路径定义为无人机从起始点到终点所飞行路程的值,设一条完整的航线有 n n n个节点,其中第 i i i个航路点和第 i + 1 i+1 i+1个航路点之间的距离表示为 l i l_i li ,这两个航路点的坐标分别表示为 ( x i , y i , z i ) (x_i,y_i,z_i ) (xi,yi,zi), ( x i + 1 , y i + 1 , z i + 1 ) (x_{i+1}, y_{i+1},z_{i+1}) (xi+1,yi+1,zi+1)并分别记作 g ( i ) g(i) g(i)和 g ( i + 1 ) g(i+1) g(i+1)。航迹需要满足如下条件:
{ l i = ∣ ∣ g ( i + 1 ) − g ( i ) ∣ ∣ 2 L p a t h = ∑ i = 1 n − 1 l i (4) \begin{cases} l_i = ||g(i+1)-g(i)||_2\\ L_{path}=\sum_{i=1}^{n-1}l_i \end{cases}\tag{4} {li=∣∣g(i+1)−g(i)∣∣2Lpath=∑i=1n−1li(4)
在飞行的过程中会遇到障碍物或者进入威胁区域,如果无人机无法躲避障碍物或者飞入了威胁区域将面临被击落或坠毁的危险以至于无法到达终点,记为 L p a t h = ∞ L_{path}=\infty Lpath=∞,但是无穷函数在实际问题中很难表示,我们采用惩罚的方式进行处理。一般情况下,为了利用地形覆盖自身位置,无人机应尽可能降低高度这可以帮助自身避免一些未知雷达等威胁。但是太低的飞行高度同样会加大无人机同山体和地面的撞击几率,因此设定稳定的飞行高度是非常重要的。飞行高度不应该有太大的变化,稳定的飞行高度可以减少控制系统的负担,节省更多的燃料 。为了使无人机飞行更加安全,给出的飞行高度模型:
{ h h e i g h t = 1 n ∑ i = 0 n − 1 ( z ( i ) − z ‾ ) 2 z ‾ = 1 n ∑ i = 0 n − 1 z ( i ) (5) \begin{cases} h_{height}=\sqrt{\frac{1}{n}\sum_{i=0}^{n-1}(z(i)-\overline{z})^2}\\ \overline{z}=\frac{1}{n}\sum_{i=0}^{n-1}z(i) \end{cases}\tag{5} {hheight=n1∑i=0n−1(z(i)−z)2z=n1∑i=0n−1z(i)(5)
无人机的可操作性也受到其转角代价函数的限制。,在飞行过程中无人机的转角应不大于其预先设定的最大转角,转角的大小会影响其飞行的稳定性。本文的研究中,设定最大转角为 Φ Φ Φ,当前转角为 θ \theta θ并且 a i a_i ai是第 i i i段航路段向量。
{ c o s θ = a i T a i + 1 ∣ a i ∣ ∣ a i + 1 ∣ J t u r n = ∑ i = 1 n ( c o s ( Φ − c o s θ ) ) (6) \begin{cases} cos\theta =\frac{a_i^Ta_{i+1}}{|a_i||a_{i+1}|}\\ J_{turn}=\sum_{i=1}^n(cos(\Phi-cos\theta)) \end{cases}\tag{6} {cosθ=∣ai∣∣ai+1∣aiTai+1Jturn=∑i=1n(cos(Φ−cosθ))(6)
其中, ∣ a ∣ |a| ∣a∣代表矢量 a a a的长度。
? 通过对以上三个方面建立了无人机航迹规划的代价函数,可以得出本文的航迹评价函数如下:
J c o s t = w 1 L p a t h + w 2 h h e i g h t + w 3 J t u r n (7) J_{cost}=w_1L_{path}+w_2h_{height}+w_3J_{turn} \tag{7} Jcost=w1Lpath+w2hheight+w3Jturn(7)
其中, J c o s t J_{cost} Jcost是总的代价函数,参数 w i w_i wi , i = 1 , 2 , 3 i=1,2,3 i=1,2,3 表示每个代价函数的权值,且满足如下条件:
{ w i ≥ 0 ∑ i = 1 3 w i = 1 (8) \begin{cases} w_i\geq0 \\ \sum_{i=1}^3 w_i=1 \end{cases} \tag{8} {wi≥0∑i=13wi=1(8)
通过对总的代价函数进行有效地处理,我们可以得到由线段组成的航迹。不可否认的是得到的路径往往是仅在理论上可行,但为了实际可飞,有必要对航迹进行平滑处理。本文采用三次样条插值的方法对路径进行平滑。
4.实验结果
4.1地图创建
设置地图参数a, b, c, d, e, f , g=1。地图大小为:200*200。设置三个山峰,山峰信息如表1所示。威胁区域信息如表2所示
| 信息 | 山峰中心坐标 | 山峰高度 | 山峰X方向坡度 | 山峰y方向坡度 |
|---|---|---|---|---|
| 山峰1 | [60,60] | 50 | 20 | 20 |
| 山峰2 | [100,100] | 60 | 30 | 30 |
| 山峰3 | [150,150] | 80 | 20 | 20 |
| 信息 | 威胁区域中心坐标 | 威胁区域半径 |
|---|---|---|
| 威胁区域1 | [150,50] | 30 |
| 威胁区域2 | [50,150] | 20 |
创建的地图如下:

4.2 航迹规划
设置起点坐标为[0,0,20],终点坐标为[200,200,20]。利用回溯搜索算法对航迹评价函数式(7)进行优化。优化结果如下:

从结果来看,回溯搜索算法规划出了一条比较好的路径,表明算法具有一定的优势。
5.参考文献
[1]薛建凯. 一种新型的群智能优化技术的研究与应用[D].东华大学,2020.DOI:10.27012/d.cnki.gdhuu.2020.000178.
6.Matlab代码
相关文章:

基于回溯搜索算法的无人机航迹规划-附代码
基于回溯搜索算法的无人机航迹规划 文章目录 基于回溯搜索算法的无人机航迹规划1.回溯搜索搜索算法2.无人机飞行环境建模3.无人机航迹规划建模4.实验结果4.1地图创建4.2 航迹规划 5.参考文献6.Matlab代码 摘要:本文主要介绍利用回溯搜索算法来优化无人机航迹规划。 …...

微信小程序云开发笔记-初始化商城小程序
缘起:由于痴迷机器人,店都快倒闭了,没办法,拿出点精力给店里搞个小程序,要多卖货才能活下来搞机器人,在此记录一下搞小程序的过程,要不然搞完又忘了。腾讯的云开发,前端和后端都有了…...
vulnhub_DeRPnStiNK靶机渗透测试
VulnHub2018_DeRPnStiNK靶机 https://www.vulnhub.com/entry/derpnstink-1,221/ flag1(52E37291AEDF6A46D7D0BB8A6312F4F9F1AA4975C248C3F0E008CBA09D6E9166) flag2(a7d355b26bda6bf1196ccffead0b2cf2b81f0a9de5b4876b44407f1dc07e51e6) flag4(49dca65f362fee401292ed7ada96f9…...

网站如何判断请求是来自手机-移动端还是PC-电脑端?如何让网站能适应不同的客户端?
如果网站需要实现手机和PC双界面适应,可以有两种方式: 第一种是响应式界面,根据屏幕宽度来判定显示的格式。这种需要前端来做,手机/PC共用一套代码,有一定的局限性。 第二种是后端通过request请求头中的内容来分析客户…...

sass和 scss的区别?
Sass(Syntactically Awesome Style Sheets)和 SCSS(Sassy CSS)是两种流行的 CSS 预处理器,它们扩展了普通的 CSS 语法,提供了更多的功能和便利性。下面是 Sass 和 SCSS 的主要区别: 1ÿ…...
Vuex 动态模块状态管理器
模块化思想 我们之前的博文已经讲述了Vuex怎么使用命名空间实现模块化状态管理。详情可以看: Vuex命名空间及如何获取根模块、兄弟模块状态管理器_AI3D_WebEngineer的博客-CSDN博客https://blog.csdn.net/weixin_42274805/article/details/133269196?ops_request_…...
实现分片上传、断点续传、秒传 (JS+NodeJS)(TypeScript)
一、引入及效果 上传文件是一个很常见的操作,但是当文件很大时,上传花费的时间会非常长,上传的操作就会具有不确定性,如果不小心连接断开,那么文件就需要重新上传,导致浪费时间和网络资源。 所以࿰…...
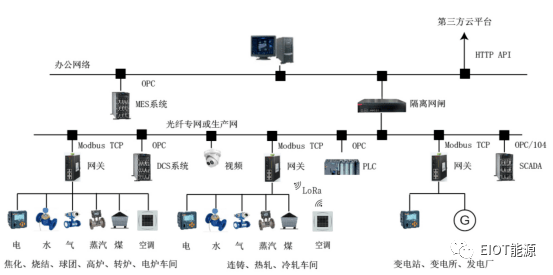
浅谈安科瑞EMS能源管控平台建设的意义-安科瑞 蒋静
摘 要:能源消耗量大、能源运输供给不足、环境压力日趋增加、能耗双控等一系列问题一直困扰着钢铁冶金行业,制约着企业快速稳定健康发展。本文介绍的安科瑞EMS能源管控平台,采用自动化、信息化技术,实现从能源数据采集、过程监控、…...

【原创】指针变量作为函数参数要点注意+main函数中值是否改变
指针变量作为函数参数要点注意(已写至笔记) 1传参指针不加*(main中函数) 2收参指针要加*(被main调用的函数) 3传参指针名可与收参指针名不同,不影响 4【问】如何看主函数中指针所指内容是否改变…...
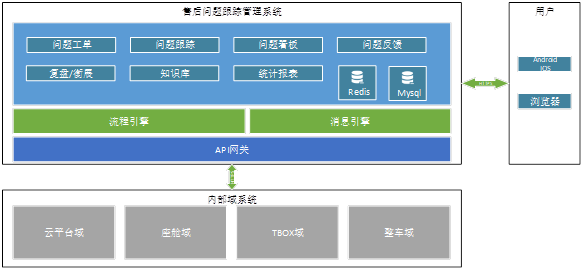
售后处置跟踪系统设想
售后处置跟踪系统设想 前言 随着汽车工业的发展,软件定义车的模式已成为主流汽车设计及智能化功能架构模式,通过引入SOA的软件架构设计,使得现有的座舱软件、云端服务软件、App软件等众多功能模块的版本迭代频次日新月异,发版更…...

python实现ModBusTCP协议的server
python实现ModBusTCP协议的server是一件简单的事情,只要通过pymodbus、pyModbusTCP等模块都可以实现,本文采用pymodbus。 相关文章见: python实现ModBusTCP协议的client-CSDN博客 一、了解pymodbus的Server 1、pymodbus.server的模块 pym…...

AndroidStudio编译错误‘android.injected.build.density‘ is deprecated
问题 AndroidStudio编译错误 The option ‘android.injected.build.density’ is deprecated. It was removed in version 8.0 of the Android Gradle plugin. Density property injection from Android Studio has been removed. 解决 app/build.gradle 中这行 apply plugi…...
计网小题题库整理第一轮(面向期末基础)(3)
基础选择题的最后一章更新,看完期末75至少没问题~ 前情提要: 计网小题题库整理第一轮(12期) 一.选择题 1、 目前,最流行的以太网组网的拓扑结构是( C )。 A) 总线结构 B) 环…...
进程控制(一):进程终止
文章目录 进程控制(一)进程终止运行正常退出码 运行异常进程正常/异常总结 进程控制(一) 在前文中,我们初步了解了进程的概念,以及通过fork函数来创建子进程,并对于为什么运行一个程序…...
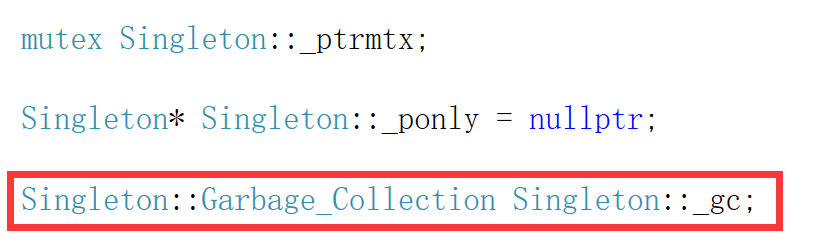
特殊类设计[下] --- 单例模式
文章目录 5.只能创建一个对象的类5.1设计模式[2.5 万字详解:23 种设计模式](https://zhuanlan.zhihu.com/p/433152245)5.2单例模式1.饿汉模式1.懒汉模式 6.饿汉模式7.懒汉模式7.1饿汉模式优缺点:7.2懒汉模式1.线程安全问题2.单例对象的析构问题 8.整体代码9.C11后可…...
)
计算机网络-应用层(1)
一、DNS 域名系统 (DNS) 是把主机域名解析为IP地址的系统。该系统是由解析器和域名服务器组成的。采用UDP 协议,较少情况下使用TCP 协议,端口号均为53。 域名系统由三部分构成: DNS 名字空间、域名服务器、 DNS客户机。 (1)根域:…...

Kotlin基础——枚举、When、in、for
枚举 声明只有值的枚举 enum class Color {RED, GREEN, BLUE }此外还可以增加属性和方法,如果需要在枚举类中定义方法,要使用分号把枚举常量列表和方法定义分开,这也是Kotlin唯一必须使用分号的地方 enum class Color(val r: Int, val g: …...
)
C++编程题目------平面上的最接近点对(分治算法)
题目描述 给定平面上n个点,找出其中的一对点的距离,使得在这n个点的所有点对中,该距离为所有点对中最小的。 输入格式 第一行一个整数 n,表示点的个数。 接下来 n 行,每行两个实数 x,y ,表示一个点的行…...

Linux下的文件操作和文件管理
文章目录 应用编程文件操作文件描述符open函数write函数read函数close函数lseek函数文件操作例子 文件管理文件基本知识文件类型文件共享空洞文件错误处理退出程序原子操作fcntl和ioctl截断文件stat函数软链接和硬链接 应用编程 系统调用(system call)是Linux内核提供给应用层…...

设计模式之桥梁模式
什么是桥梁模式 桥梁模式(Bridge Pattern)也称为桥接模式,属于结构型模式,它主要目的是通过组合的方式建立两个类之间的联系,而不是继承。桥梁模式将抽象部分与它的具体实现部分分离,使它们都可以独立地变…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...

MySQL 8.0 事务全面讲解
以下是一个结合两次回答的 MySQL 8.0 事务全面讲解,涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容,并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念(ACID) 事务是…...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...

R 语言科研绘图第 55 期 --- 网络图-聚类
在发表科研论文的过程中,科研绘图是必不可少的,一张好看的图形会是文章很大的加分项。 为了便于使用,本系列文章介绍的所有绘图都已收录到了 sciRplot 项目中,获取方式: R 语言科研绘图模板 --- sciRplothttps://mp.…...

在 Spring Boot 项目里,MYSQL中json类型字段使用
前言: 因为程序特殊需求导致,需要mysql数据库存储json类型数据,因此记录一下使用流程 1.java实体中新增字段 private List<User> users 2.增加mybatis-plus注解 TableField(typeHandler FastjsonTypeHandler.class) private Lis…...
