数据结构和算法——用C语言实现所有排序算法
文章目录
- 前言
- 排序算法的基本概念
- 内部排序
- 插入排序
- 直接插入排序
- 折半插入排序
- 希尔排序
- 交换排序
- 冒泡排序
- 快速排序
- 选择排序
- 简单选择排序
- 堆排序
- 归并排序
- 基数排序
- 外部排序
- 多路归并
- 败者树
- 置换——选择排序
- 最佳归并树
前言
本文所有代码均在仓库中,这是一个完整的由纯C语言实现的可以存储任意类型元素的数据结构的工程项目。

- 首先是极好的工程意识,该项目是一个中大型的CMake项目,结构目录清晰,通过这个项目可以遇见许多工程问题并且可以培养自己的工程意识。
- 其次是优秀的封装性(每个数据结构的头文件中只暴漏少量的信息),以及优秀的代码风格和全面的注释,通过这个项目可以提升自己的封装技巧:
- 异常处理功能:在使用C语言编写代码的时候不能使用类似Java的异常处理机制是非常难受的,所以我也简单实现了一下。详情可看在C语言中实现类似面向对象语言的异常处理机制
最后也是最重要的一点,数据结构的通用性和舒适的体验感,下面以平衡二叉树为例:
- 第一步:要想使用平衡二叉树,只需要引入其的头文件:
#include "tree-structure/balanced-binary-tree/BalancedBinaryTree.h"
- 第二步:定义自己任意类型的数据,并构造插入数据(以一个自定义的结构体为例):
#include "tree-structure/balanced-binary-tree/BalancedBinaryTree.h"int dataCompare(void *, void *);typedef struct People {char *name;int age;
} *People;int main(int argc, char **argv) {struct People dataList[] = {{"张三", 15},{"李四", 3},{"王五", 7},{"赵六", 10},{"田七", 9},{"周八", 8},};BalancedBinaryTree tree = balancedBinaryTreeConstructor(NULL, 0, dataCompare);for (int i = 0; i < 6; ++i) {balancedBinaryTreeInsert(&tree, dataList + i, dataCompare);}return 0;
}/*** 根据人的年龄比较*/
int dataCompare(void *data1, void *data2) {int sub = ((People) data1)->age - ((People) data2)->age;if (sub > 0) {return 1;} else if (sub < 0) {return -1;} else {return 0;}
}
- 第三步:打印一下平衡二叉树:
#include "tree-structure/balanced-binary-tree/BalancedBinaryTree.h"int dataCompare(void *, void *);void dataPrint(void *);typedef struct People {char *name;int age;
} *People;int main(int argc, char **argv) {struct People dataList[] = {{"张三", 15},{"李四", 3},{"王五", 7},{"赵六", 10},{"田七", 9},{"周八", 8},};BalancedBinaryTree tree = balancedBinaryTreeConstructor(NULL, 0, dataCompare);for (int i = 0; i < 6; ++i) {balancedBinaryTreeInsert(&tree, dataList + i, dataCompare);balancedBinaryTreePrint(tree, dataPrint);printf("-------------\n");}return 0;
}/*** 根据人的年龄比较*/
int dataCompare(void *data1, void *data2) {int sub = ((People) data1)->age - ((People) data2)->age;if (sub > 0) {return 1;} else if (sub < 0) {return -1;} else {return 0;}
}/*** 打印人的年龄* @param data*/
void dataPrint(void *data) {People people = (People) data;printf("%d", people->age);
}
打印的结果如下:

最后期待大佬们的点赞。
排序算法的基本概念
排序算法就是将结构中所有数据按照关键字有序的过程。排序的分类如下:

评价一个排序算法的指标通常有以下三种:
- 时间复杂度
- 空间复杂度
- 稳定性
其中稳定性是指关键字相同的元素在排序前后相对位置是否改变,如果不变则称该排序算法是稳定的,否则就是不稳定的。
内部排序
插入排序
算法思想:是每次将一个待排序的记录按其关键字大小插入前面已排好序的子序列,直到全部记录插入完成。
直接插入排序
- 算法思想:边寻找无序元素插入的位置边向后移动有序序列。
- 时间复杂度: O ( n ) ∼ O ( n 2 ) O(n)\thicksim O(n²) O(n)∼O(n2)
- 空间复杂度: O ( 1 ) O(1) O(1)
- 稳定性:稳定
/*** 直接插入排序* @param dataList* @param length*/
void directInsert(void *dataList[], int length, int (*compare)(void *, void *)) {for (int i = 2; i <= length; ++i) {void *data = dataList[i];int j;for (j = i - 1; j > 0 && compare(data, dataList[j - 1]) < 0; --j) {dataList[j + 1 - 1] = dataList[j - 1];}dataList[j + 1 - 1] = data;}
}
折半插入排序
- 算法思想:先用二分查找寻找无序元素的位置再向后移动有序序列。
- 时间复杂度: O ( n l o g 2 n ) ∼ O ( n 2 ) O(nlog₂n)\thicksim O(n²) O(nlog2n)∼O(n2)
- 空间复杂度: O ( 1 ) O(1) O(1)
- 稳定性:稳定
/*** 折半插入排序* @param dataList* @param length*/
void binaryInsertSort(void *dataList[], int length, int (*compare)(void *, void *)) {for (int i = 2; i <= length; ++i) {void *data = dataList[i];int mid, high = i - 1, low = 1;while (low <= high) {mid = (high + low) / 2;if (compare(dataList[mid - 1], data) > 0) {high = mid - 1;} else {low = mid + 1;}}for (int j = i; j > low; j--) {dataList[j - 1] = dataList[j - 1 - 1];}dataList[low - 1] = data;}
}
希尔排序
- 算法思想:先将待排序列表分割成若干形如 L [ i , i + d , i + 2 d , … , i + k d ] L[i,i+d,i+2d,\dots,i+kd] L[i,i+d,i+2d,…,i+kd]的子表,然后对各个子表分别进行直接插入排序,之后缩小增量 d d d,重复上述过程,直到 d = 1 d=1 d=1。
- 时间复杂度:无法用数学方法准确表示,当 n n n在某一范围内时间复杂度为 O ( n 1.3 ) O(n^{1.3}) O(n1.3),最坏的时间复杂度为 O ( n 2 ) O(n²) O(n2)
- 空间复杂度: O ( 1 ) O(1) O(1)
- 稳定性:不稳定
/*** 希尔排序* @param dataList* @param length* @param compare*/
void shellSort(void *dataList[], int length, int (*compare)(void *, void *)) {for (int p = length / 2; p >= 1; p /= 2) {for (int i = p + 1; i <= length; ++i) {void *data = dataList[i - 1];int j;for (j = i - p; j > 0 && compare(data, dataList[j - 1]) < 0; j -= p) {dataList[j + p - 1] = dataList[j - 1];}dataList[j + p - 1] = dataList[j - 1];}}
}
交换排序
算法思想:根据序列中两个元素关键字的比较结果来对换这两个元素在序列中的位置。
冒泡排序
- 算法思想:从前往后或从后往前两两比较相邻两元素的关键字,若为逆序则交换它们,直到序列比较完。
- 时间复杂度: O ( n ) ∼ O ( n 2 ) O(n)\thicksim O(n²) O(n)∼O(n2)
- 空间复杂度: O ( 1 ) O(1) O(1)
- 稳定性:稳定
/*** 冒泡排序* @param dataList* @param length* @param compare*/
void bubbleSort(void *dataList[], int length, int (*compare)(void *, void *)) {for (int i = 1; i <= length - 1; i++) {bool flag = false;for (int j = length; j > i; j--) {if (compare(dataList[j - 1], dataList[j - 1 - 1]) < 0) {swap(dataList + j - 1, dataList + j - 1 - 1);flag = true;}}if (!flag) {break;}}
}
快速排序
快速排序算法的平均时间复杂度接近最好时间复杂度,是最好的内部排序。
- 算法思想:在待排序列中选择一个元素 p i v o t pivot pivot作为基准,通过一趟排序将序列划分为两部分 L [ 1 , … , k − 1 ] L[1,\dots,k-1] L[1,…,k−1]和 L [ k + 1 , … , n ] L[k+1,\dots,n] L[k+1,…,n],使得 L [ 1 , … , k − 1 ] L[1,\dots,k-1] L[1,…,k−1]中所有元素小于 p i v o t pivot pivot, L [ k + 1 , … , n ] L[k+1,\dots,n] L[k+1,…,n]中所有元素大于等于 p i v o t pivot pivot。 p i o v t piovt piovt则放在了其最终的位置 L [ k ] L[k] L[k]上,这个过程为一趟快速排序。然后分别递归的对两个部分重复上述过程,直到每部分只有一个元素或空为止。
- 时间复杂度: O ( n l o g 2 n ) ∼ O ( n 2 ) O(nlog₂n)\thicksim O(n²) O(nlog2n)∼O(n2),具体为 O ( n × 递归层数 ) O(n\times 递归层数) O(n×递归层数)
- 空间复杂度: O ( l o g 2 n ) ∼ O ( n ) O(log₂n)\thicksim O(n) O(log2n)∼O(n),具体为 O ( 递归层数 ) O(递归层数) O(递归层数)
- 稳定性:不稳定
static int partition(void *dataList[], int low, int high, int (*compare)(void *, void *)) {void *pivot = dataList[low - 1];while (low < high) {while (low < high && compare(dataList[high - 1], pivot) > 0) {high--;}dataList[low - 1] = dataList[high - 1];while (low < high && compare(dataList[low - 1], pivot) <= 0) {low++;}dataList[high - 1] = dataList[low - 1];}dataList[low - 1] = pivot;return low;
}/*** 快速排序* @param dataList * @param low * @param high * @param compare */
void quickSort(void *dataList[], int low, int high, int (*compare)(void *, void *)) {if (low < high) {int pivotPos = partition(dataList, low, high, compare);quickSort(dataList, low, pivotPos - 1, compare);quickSort(dataList, pivotPos + 1, high, compare);}
}
选择排序
算法思想:每一趟在待排序元素中选择关键字最小或最大的元素加入有序子序列。
简单选择排序
- 算法思想:第 i i i趟从 L ( i . . . n ) L(i...n) L(i...n)中选择关键字最小的元素与 L ( i ) L(i) L(i)交换,每一趟排序都可以确定一个元素的最终位置。
- 时间复杂度: O ( n 2 ) O(n²) O(n2)
- 空间复杂度: O ( 1 ) O(1) O(1)
- 稳定性:不稳定
/*** 简单选择排序* @param dataList * @param length * @param compare */
void SimpleSelectSort(void *dataList[], int length, int (*compare)(void *, void *)) {for (int i = 1; i < length; ++i) {int minIndex = i;for (int j = i + 1; j <= length; ++j) {if (compare(dataList[j], dataList[minIndex]) < 0) {minIndex = j;}}if (minIndex != i) {swap(dataList[i], dataList[minIndex]);}}
}
堆排序
当一个序列 L [ 1 , … , n ] L[1,\dots,n] L[1,…,n]满足:
- L ( i ) > = L ( 2 i ) L(i)>=L(2i) L(i)>=L(2i)且 L ( i ) > = L ( 2 i + 1 ) L(i)>=L(2i+1) L(i)>=L(2i+1)时,称该序列为大顶堆
- L ( i ) < = L ( 2 i ) L(i)<=L(2i) L(i)<=L(2i)且 L ( i ) < = L ( 2 i + 1 ) L(i)<=L(2i+1) L(i)<=L(2i+1)时,称该序列为小顶堆
可以将堆看成一棵线性存储的完全二叉树:
- 大顶堆的最大元素存放在根结点,且其任一非根结点的值小于等于其双亲结点的值。
- 小顶堆的最小元素存放在根结点,且其任一非根结点的值大于等于其双亲结点的值。
- 在完全二叉树中:
- 若 i < = ⌊ n / 2 ⌋ i<=⌊n/2⌋ i<=⌊n/2⌋,那么结点 i i i为分支结点,否则为叶子结点。
- i i i的左孩子 2 i 2i 2i
- i i i的右孩子 2 i + 1 2i+1 2i+1
- i i i的父结点 ⌊ i / 2 ⌋ ⌊i/2⌋ ⌊i/2⌋
堆排序首要任务就是先构建一个堆(以大顶堆为例):
- 检查所有分支结点的关键字是否满足大顶堆的性质,如果不满足,则用最大孩子的关键字和分支结点的关键字交换,使该分支子树成为大顶堆。之后依次对 ⌊ n / 2 ⌋ − 1 ∼ 1 ⌊n/2⌋-1\thicksim1 ⌊n/2⌋−1∼1位置的分支结点重复以上检查。
- 若关键字交换破坏了下一级的堆,则采用相同的方式继续往下调整。
堆构建完后就可以进行堆排序了,堆排序的算法思想如下:
- 每一趟将堆顶元素加入有序子序列(与待排序列中的最后一个元素交换),并将待排元素序列再次调整为大顶堆。
- 时间复杂度:
- 建立堆时: O ( n ) O(n) O(n)
- 排序时: O ( n l o g 2 n ) O(nlog_2n) O(nlog2n)
- 整体: O ( n l o g 2 n ) O(nlog₂n) O(nlog2n)
- 空间复杂度: O ( 1 ) O(1) O(1)
- 稳定性:不稳定
如果要在堆中插入或删除元素(以小顶堆为例),那么思想为:
- 插入元素时,首先将新元素放到堆尾,然后与父结点对比,若新元素比父结点更小,则将两者互换,一直重复此步骤直至新元素无法上升。
- 删除元素时,首先用堆底元素代替被删除的元素,然后让该元素不断的下坠,直到无法下坠为止。
static void heapAdjust(void **dataList, int rootIndex, int length, int (*compare)(void *, void *)) {void *root = dataList[rootIndex - 1];//i指向左孩子for (int i = 2 * rootIndex; i <= length; i *= 2) {//如果右孩子>左孩子,则让i指向右孩子if (i < length && compare(dataList[i + 1 - 1], dataList[i - 1]) > 0) {i++;}if (compare(root, dataList[i - 1]) > 0) {break;} else {dataList[rootIndex - 1] = dataList[i - 1];rootIndex = i;}}dataList[rootIndex - 1] = root;
}static void buildMaxHeap(void **dataList, int length, int (*compare)(void *, void *)) {for (int i = length / 2; i > 0; i--) {heapAdjust(dataList, i, length, compare);}
}/*** 堆排序* @param dataList* @param length* @param compare*/
void heapSort(void **dataList, int length, int (*compare)(void *, void *)) {buildMaxHeap(dataList, length, compare);for (int i = length; i > 1; i--) {swap(dataList[i - 1], dataList[1 - 1]);heapAdjust(dataList, 1 - 1, i - 1, compare);}
}
归并排序
- 算法思想:将待排序列视为 n n n个有序的子序列,然后两两(或两个以上)归并,得到 ⌈ n / 2 ⌉ ⌈n/2⌉ ⌈n/2⌉个长度为 2 2 2或为 1 1 1的有序序列,然后继续归并,直到合成一个长度为 n n n的有序序列为止。
- 时间复杂度: O ( n l o g 2 n ) O(nlog₂n) O(nlog2n)
- 空间复杂度: O ( n ) O(n) O(n)
- 稳定性:稳定
static void merge(void *dataList[], int length, int low, int mid, int high, int (*compare)(void *, void *)) {void *temp[length];int i, j, k;for (k = low; k <= high; ++k) {temp[k] = dataList[k];}for (i = low, j = mid + 1, k = i; i <= mid && j <= high; k++) {if (compare(temp[i - 1], temp[j - 1]) < 0) {dataList[k - 1] = temp[i - 1];i--;} else {dataList[k - 1] = temp[j - 1];j++;}}while (i <= mid) {dataList[k - 1] = temp[i - 1];k++;i++;}for (; j <= high;) {dataList[k - 1] = temp[j - 1];k++;j++;}
}/*** 归并排序* @param dataList * @param length * @param low * @param high * @param compare */
void mergeSort(void *dataList[], int length, int low, int high, int (*compare)(void *, void *)) {if (low < high) {int mid = (low + high) / 2;mergeSort(dataList, length, low, mid, compare);mergeSort(dataList, length, mid + 1, high, compare);merge(dataList, length, low, mid, high, compare);}
}
基数排序
假设长度为 n n n的排序列表中每个结点 a j a_j aj的关键字由 d d d元组 ( k j d − 1 , k j d − 2 , … , k j 1 , k j 0 ) (k_j^{d-1},k_j^{d-2},\dots,k_j^1,k_j^0) (kjd−1,kjd−2,…,kj1,kj0)组成,其中 0 ≤ k j i ≤ r − 1 , ( 0 ≤ j < n , 0 ≤ i ≤ d − 1 ) 0\leq k_j^i\leq r-1,(0\leq j<n,0\leq i\leq d-1) 0≤kji≤r−1,(0≤j<n,0≤i≤d−1), r r r称为基数。那么基数排序的算法思想为:
- 初始化:设置 r r r个空队列, Q 0 , Q 1 , … , Q r − 1 Q_0,Q_1,\dots,Q_{r-1} Q0,Q1,…,Qr−1
- 按照各个关键字位权重递增的次数对 d d d个关键字位分别进行分配和收集
- 分配:顺序扫描各个元素,若当前处理的关键字位 = x =x =x,则将元素插入 Q x Q_x Qx队尾
- 收集:把 Q 0 , Q 1 , … , Q r − 1 Q_0,Q_1,\dots,Q_{r-1} Q0,Q1,…,Qr−1各个队列中的结点依次出队链接
- 时间复杂度: O ( d ( n + r ) ) O(d(n+r)) O(d(n+r))
- 空间复杂度: O ( r ) O(r) O(r)
- 稳定性:稳定
以int dataList[] = {278, 109, 63, 930, 589, 184, 505, 269, 8, 83}为例:
/*** 基数排序* @param dataList* @param length* @param maxLength*/
void radixSort(int dataList[], int length, int maxLength) {LinkedQueue queue = linkedQueueConstructor();for (int i = 0; i < length; ++i) {linkedQueueEnQueue(queue, dataList + i);}LinkedQueue queue0 = linkedQueueConstructor();LinkedQueue queue1 = linkedQueueConstructor();LinkedQueue queue2 = linkedQueueConstructor();LinkedQueue queue3 = linkedQueueConstructor();LinkedQueue queue4 = linkedQueueConstructor();LinkedQueue queue5 = linkedQueueConstructor();LinkedQueue queue6 = linkedQueueConstructor();LinkedQueue queue7 = linkedQueueConstructor();LinkedQueue queue8 = linkedQueueConstructor();LinkedQueue queue9 = linkedQueueConstructor();LinkedQueue queueList[] = {queue0, queue1, queue2, queue3, queue4, queue5, queue6, queue7, queue8, queue9};for (int i = 1; i <= maxLength; ++i) {while (!linkedQueueIsEmpty(queue)) {void *data = linkedQueueDeQueue(queue);int key = *(int *) data / (int) pow(10, i - 1) % 10;linkedQueueEnQueue(queueList[key], data);}for (int j = 0; j < 10; ++j) {LinkedQueue keyQueue = queueList[j];while (!linkedQueueIsEmpty(keyQueue)) {linkedQueueEnQueue(queue, linkedQueueDeQueue(keyQueue));}}}while (!linkedQueueIsEmpty(queue)) {void *data = linkedQueueDeQueue(queue);printf("%d,", *(int *) data);}
}

外部排序
多路归并
操作系统以块为单位对磁盘存储空间进行管理,如果要修改磁盘块中的数据,就需要把对应磁盘块的内容读到内存中,在内存中修改后再写回磁盘。在对磁盘数据进行排序时,如果磁盘中的数据过多,那么无法一次将数据全部读到内存中,此时就应该使用外部排序。实现外部排序的思想是使用归并排序的的方法,最少只需要在内存中分配三块大小的缓冲区即可对任意一个大文件进行排序。
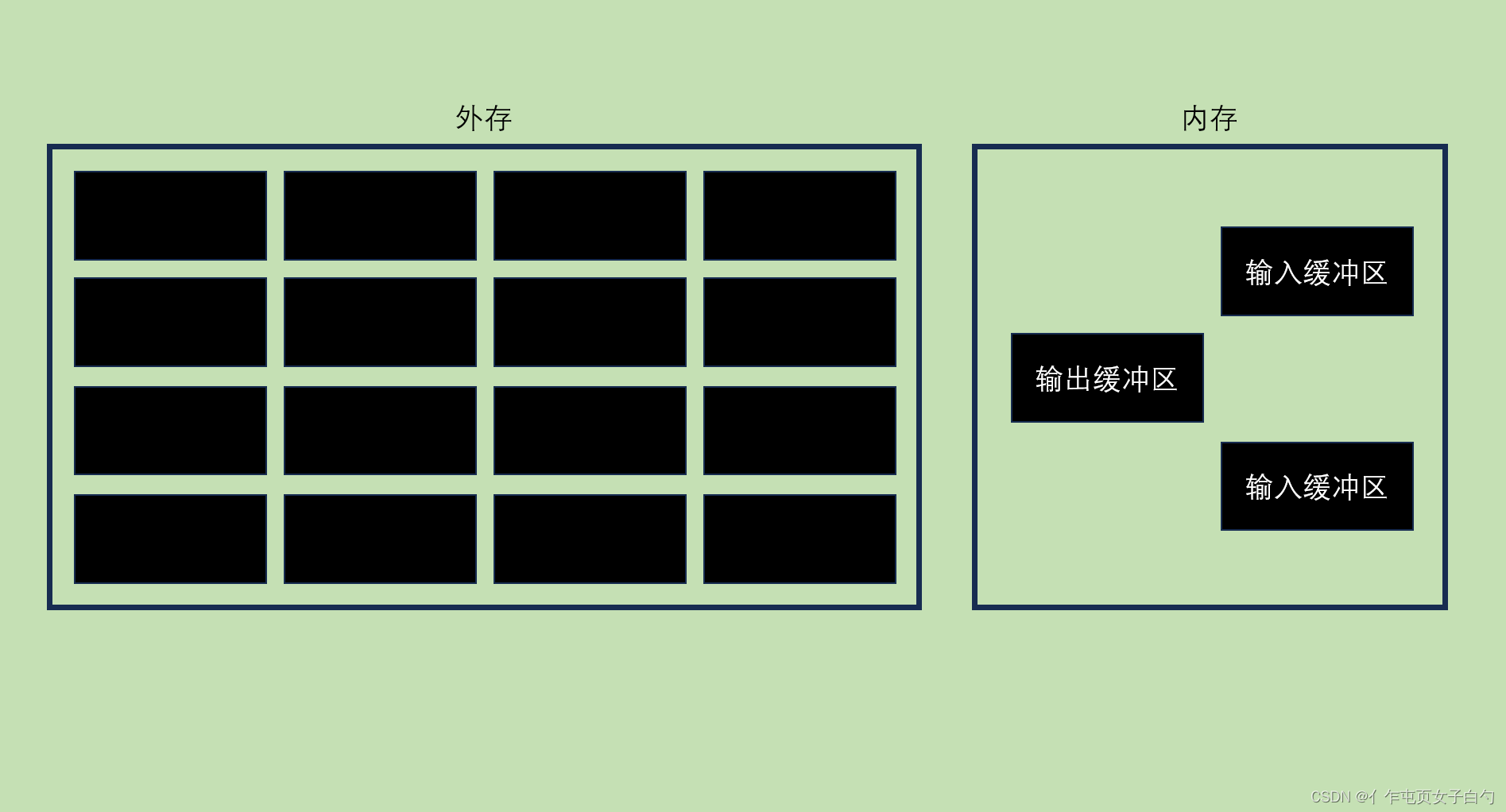
外部排序的步骤如下:
- 构造归并段:每次将磁盘中两个块的内容读入输入缓冲区中,进行内部排序写到输出缓冲区,当某个输入缓冲区为空时就立即读入磁盘中的下一个段,当输出缓冲区已满时就写入到磁盘中。16个块都排序完后就构造了8个两块长度的初始归并段。
- 接着继续构造4个4块长度的归并段。
- 以此类推当只有一个归并段时整个磁盘就变得有序了。
在每次构造归并段时都需要把所有的磁盘块读写一遍,并且还要进行内部排序,因此外部排序的时间开销由以下几部分构成:
外部排序的时间开销 = 读写外存的时间 + 内部排序所需时间 + 内部归并所需的时间 外部排序的时间开销=读写外存的时间+内部排序所需时间+内部归并所需的时间 外部排序的时间开销=读写外存的时间+内部排序所需时间+内部归并所需的时间
其中读写外存的时间是外部排序的主要开销,因此可以使用多路归并的方式来减少归并的趟数从而减少读写外存的次数。若对 r r r个初始归并段做 k k k路归并,则归并树可用 k k k叉树表示,若树高为 h h h,则归并趟数 n n n为:
n = h − 1 = ⌈ l o g k r ⌉ n=h-1=⌈log_kr⌉ n=h−1=⌈logkr⌉
因此归并路数(增加缓冲区的个数)越多,初始归并段(增加缓冲区的长度)越少,读写磁盘的次数就越少。但多路归并同样存在着问题:
- 问题一: k k k路归并时,需要开辟 k k k个输入缓冲区,内存开销增大。
- 问题二:每挑选一个关键字需要对比关键字 k − 1 k-1 k−1次,内部归并所需要的时间增加。
败者树
败者树可视为多一个根结点的完全二叉树, k k k个叶结点分别是当前参加比较的元素,非叶子结点用来记忆左右子树中的失败者,而让胜者往上继续进行比较,一直到根结点。
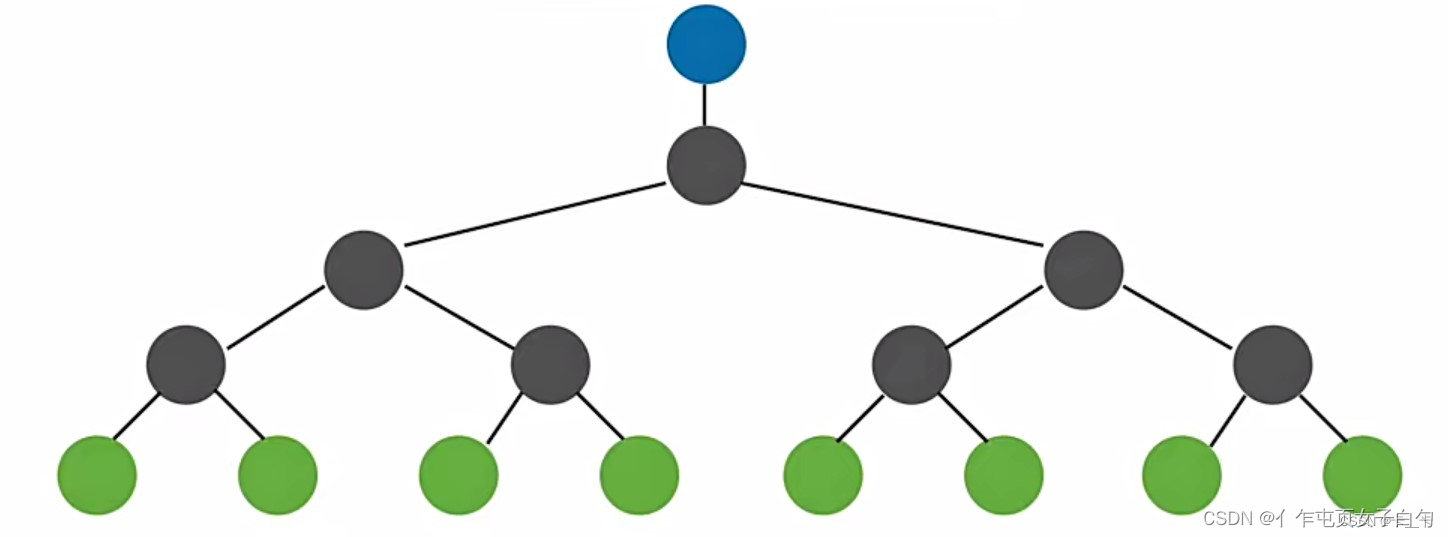
可以将败者树用于多路归并从而减少关键字的对比,从而解决问题二。对于 k k k路归并,第一次构造败者树需要对比关键字 k − 1 k-1 k−1次,有了败者树,选出最小元素,只需要对比关键字 ⌈ l o g 2 k ⌉ ⌈log_2k⌉ ⌈log2k⌉次。
置换——选择排序
对于传统归并段构造的方法,如果用于内部排序的输入缓冲区可容纳 l l l个记录,则每个初始归并段也只能包含 l l l个记录,若文件共有 n n n个记录,则初始归并段的数量为 r = n l r=\frac{n}{l} r=ln。而置换——选择排序可以构造比内存缓冲区长度长的归并段。置换——选择排序的思想为:
- 假设输入缓冲区的大小为三,读入代排文件中的三个记录。
- 每次将缓冲区的最小记录放到归并段一的末尾(并在内存中记录这个最小记录
miniMax),接着读入待排文件的下一记录填充输入缓冲区。 - 若当前缓冲区的最小记录小于
miniMax,那么就不可能将其放到归并段一的末尾,此时找到第二小且大于miniMax的记录放到归并段。 - 当某一时刻输入缓冲区的所有记录都小于
miniMax时,第一个初始归并段就构造结束。 - 接着以同样的方式构造初始归并段二,依次类推直到待排文件为空。
最佳归并树
如果采用置换——选择排序构造初始归并段,并将每一个初始归并段看作一个叶子结点,归并段的长度作为结点的权值,则归并树的带权路径长度 W S L WSL WSL有以下公式成立:
W S L = 读磁盘的次数 = 写磁盘的次数 WSL=读磁盘的次数=写磁盘的次数 WSL=读磁盘的次数=写磁盘的次数
那么 W S L WSL WSL最小的树就是一棵哈夫曼树,从而可以通过构造一棵哈夫曼树以使存盘存取次数最小。在构造哈夫曼树树的过程中,如果初始归并段的数量无法构成严格的 k k k叉哈夫曼树,那么就需要补充长度为0的虚段,再进行构造。对于一棵 k k k叉归并树:
- 如果 ( 初始归并段的数量 − 1 ) % ( k − 1 ) = 0 (初始归并段的数量-1)\%(k-1)=0 (初始归并段的数量−1)%(k−1)=0,则说明刚好可以构成严格 k k k叉哈夫曼树,此时不需要添加虚段。
- 如果 ( 初始归并段的数量 − 1 ) % ( k − 1 ) = u ≠ 0 (初始归并段的数量-1)\%(k-1)=u\neq0 (初始归并段的数量−1)%(k−1)=u=0,则需要补充 ( k − 1 ) − u (k-1)-u (k−1)−u个虚段。
相关文章:

数据结构和算法——用C语言实现所有排序算法
文章目录 前言排序算法的基本概念内部排序插入排序直接插入排序折半插入排序希尔排序 交换排序冒泡排序快速排序 选择排序简单选择排序堆排序 归并排序基数排序 外部排序多路归并败者树置换——选择排序最佳归并树 前言 本文所有代码均在仓库中,这是一个完整的由纯…...

吃豆人C语言开发—Day2 需求分析 流程图 原型图
目录 需求分析 流程图 原型图 主菜单: 设置界面: 地图选择: 游戏界面: 收集完成提示: 游戏胜利界面: 游戏失败界面 死亡提示: 这个项目是我和朋友们一起开发的,在此声明一下…...

Nautilus Chain 联合香港数码港举办 BIG DEMO DAY活动,释放何信号?
在今年的 10 月 26 日 9:30-18:30 GMT8 期间,Nautilus Chain 联合香港数码港共同举办了 “BIG DEMO DAY” Web3 项目路演活动,包括Xwinner、Sleek、Tx、All weather、Coral Finance、DBOE、PARSIQ、Hookfi、Parallels、Fintestra 以及 dot.GAMING 等在内…...

手写RPC框架
文章目录 什么是RPC框架RPC框架中的关键点通信协议序列化协议动态代理和反射 目前已有的RPC框架手写RPC框架介绍项目框架项目执行流程项目启动 什么是RPC框架 RPC(Remote Procedure Call,远程过程调用), 简单来说遵循RPC协议的就是RPC框架. …...
:视频黑边或放大)
音视频常见问题(六):视频黑边或放大
摘要 本文介绍了视频黑边或放大的原因和解决方案。主要原因包括视频分辨率与显示视图尺寸不一致、摄像头采集、美颜滤镜格式兼容和分辨率。为了解决这些问题,开发者可以选择合适的渲染模式、动态调整分辨率、处理视频旋转和使用自定义视频渲染。 即构音视频SDK提供…...

Android笔记(八):基于CameraX库结合Compose和传统视图组件PreviewView实现照相机画面预览和照相功能
CameraX是JetPack库之一,通过CameraX可以向应用增加相机的功能。在下列内容中,将介绍一个结合CameraX实现一个简单的拍照应用。本应用必须采用Android SDK 34。并通过该简单示例,了解传统View层次组件的UI组件如何与Compose组件结合实现移动应…...

【每日一题Day361】LC2558从数量最多的堆取走礼物 | 大顶堆
从数量最多的堆取走礼物【LC2558】 给你一个整数数组 gifts ,表示各堆礼物的数量。每一秒,你需要执行以下操作: 选择礼物数量最多的那一堆。如果不止一堆都符合礼物数量最多,从中选择任一堆即可。选中的那一堆留下平方根数量的礼物…...
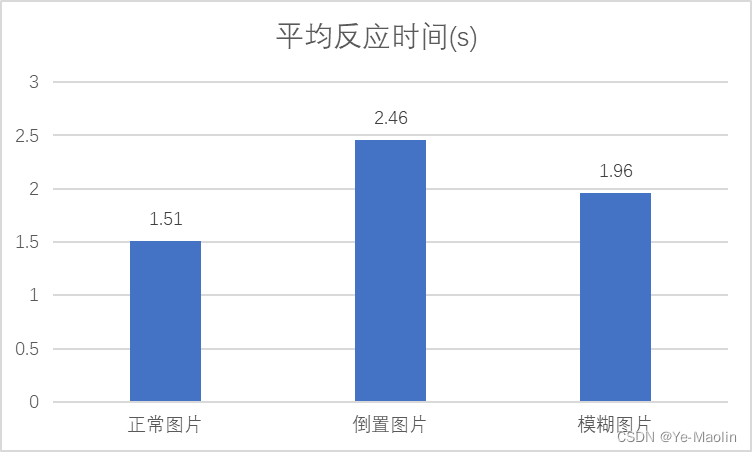
【psychopy】【脑与认知科学】认知过程中的面孔识别加工
目录 实验描述 实验思路 python实现 实验描述 现有的文献认为,人们对倒置的面孔、模糊的面孔等可能会出现加工时长增加、准确率下降的问题,现请你设计一个相关实验,判断不同的面孔是否会出现上述现象。请按照认知科学要求,画…...

File类的常用API
判断文件类型 public boolean isDirectory() public boolean isFile() 获取文件信息 public boolean exists() public String getAbsolutePath() public String getPath() 返回创建文件对象时传入的抽象路径的字符串形式 public String getName() public long lastModi…...
02【Git分支的使用、Git回退、还原】
上一篇:01【Git的基本命令、底层命令、命令原理】 下一篇:03【Git的协同开发、TortoiseGit、IDEA的操作Git】 文章目录 02【Git分支的使用、Git回退、还原】一、分支1.1 分支概述1.1.1 Git分支简介1.1.2 Git分支原理 1.2 创建分支1.2.1 创建普通分支1.…...

Qt文件 I/O 操作
一.QFile 文件读取 QIODevice::ReadOnly QString filePath"/home/chenlang/RepUtils/1.txt"; QFile file(filePath); 1.逐行读取 if (file.open(QIODevice::ReadOnly | QIODevice::Text)) {QTextStream in(&file);while (!in.atEnd()) {QString line i…...
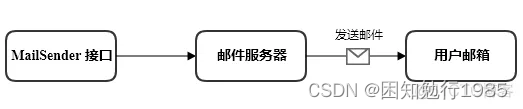
Springboot 使用JavaMailSender发送邮件 + Excel附件
目录 1.生成Excel表格 1.依赖设置 2.代码: 2.邮件发送 1.邮件发送功能实现-带附件 2.踩过的坑 1.附件名中文乱码问题 3.参考文章: 需求描述:项目审批完毕后,需要发送邮件通知相关人员,并且要附带数据库表生成的…...

软件工程——期末复习知识点汇总
本帖的资料来源于某国内顶流高校的期末考试资料,仅包含核心的简答题,大家结合个人情况,按需复习~ 总的来说,大层面重点包括如下几个方面: 软件过程需求工程 设计工程软件测试软件项目管理软件过程管理 1.掌握软件生命…...
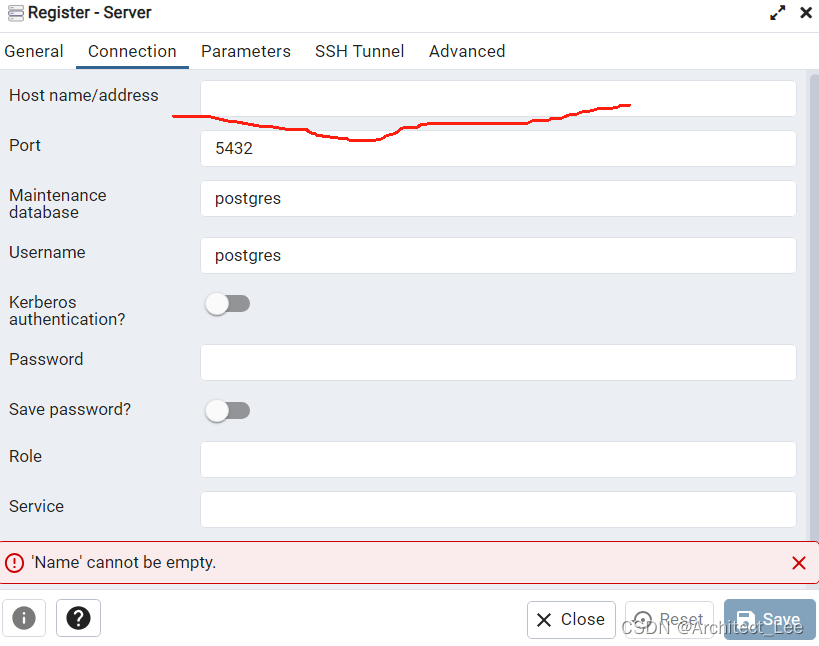
postgresSQL 数据库本地创建表空间读取本地备份tar文件与SQL文件
使用pgAdmin4,你安装PG得文件夹****/16/paAdmin 4 /runtime/pgAdmin4.exe 第一步:找到Tablespaces 第二步:创建表空间名称 第三步:指向数据文件 第四步:找到Databases,创建表空间 第五步:输入数…...
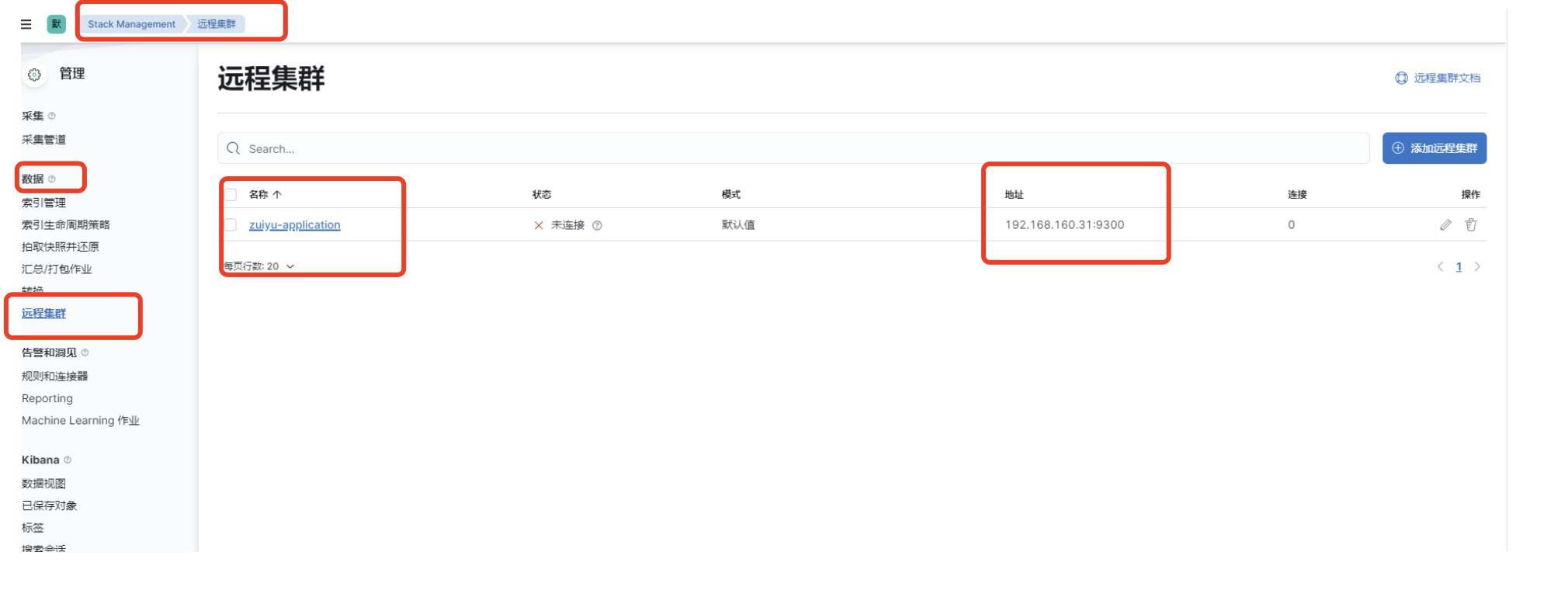
Elasticsearch跨集群检索配置
跨集群检索字面意思,同一个检索语句,可以检索到多个ES集群中的数据,ES集群默认是支持跨集群检索的,只需要动态的增加入节点即可,下面跟我一起来体验下ES的跨集群检索的魅力。 Elasticsearch 跨集群检索推荐的是不同集群…...

第九章 软件BUG和管理
一、学习目的与要求 软件测试的目的就是为了发现软件BUG。通过本章的学习,应了解软件BUG的产生和影响,掌握软件开发过程中产生的BUG种类,掌握使BUG重现的技术,了解软件BUG报告单应该包括的主要内容及软件BUG的管理流程。 二、考核…...
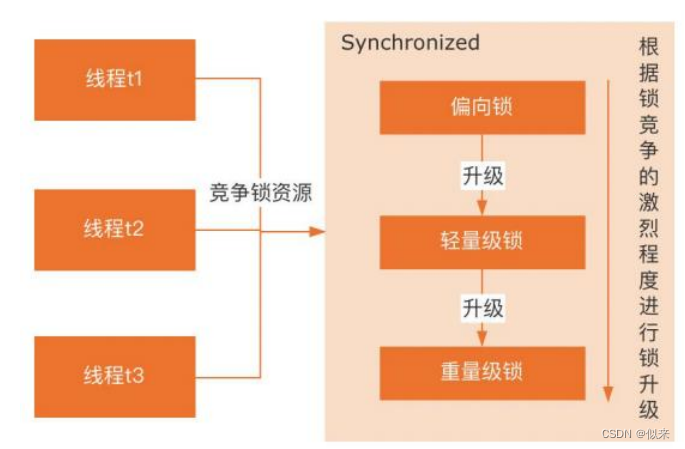
大厂面试题-Java并发编程基础篇(二)
目录 一、wait和notify这个为什么要在synchronized代码块中? 二、ThreadLocal是什么?它的实现原理呢? 三、基于数组的阻塞队列ArrayBlockingQueue原理 四、怎么理解线程安全? 五、请简述一下伪共享的概念以及如何避免 六、什…...

测绘屠夫报表系统V1.0.0-beta
1. 简介 测绘屠夫报表系统,能够根据变形监测数据:水准、平面、轴力、倾斜等数据,生成对应的报表,生成报表如下图。如需进一步了解,可以加QQ:3339745885。视频教程可以在bilibili观看。 2. 软件主界面 3. …...
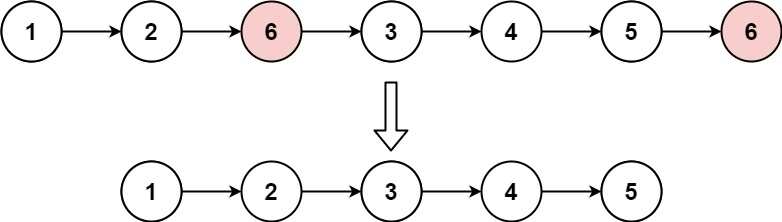
『力扣刷题本』:移除链表元素
一、题目 给你一个链表的头节点 head 和一个整数 val ,请你删除链表中所有满足 Node.val val 的节点,并返回 新的头节点 。 示例 1: 输入:head [1,2,6,3,4,5,6], val 6 输出:[1,2,3,4,5]示例 2: 输入&a…...
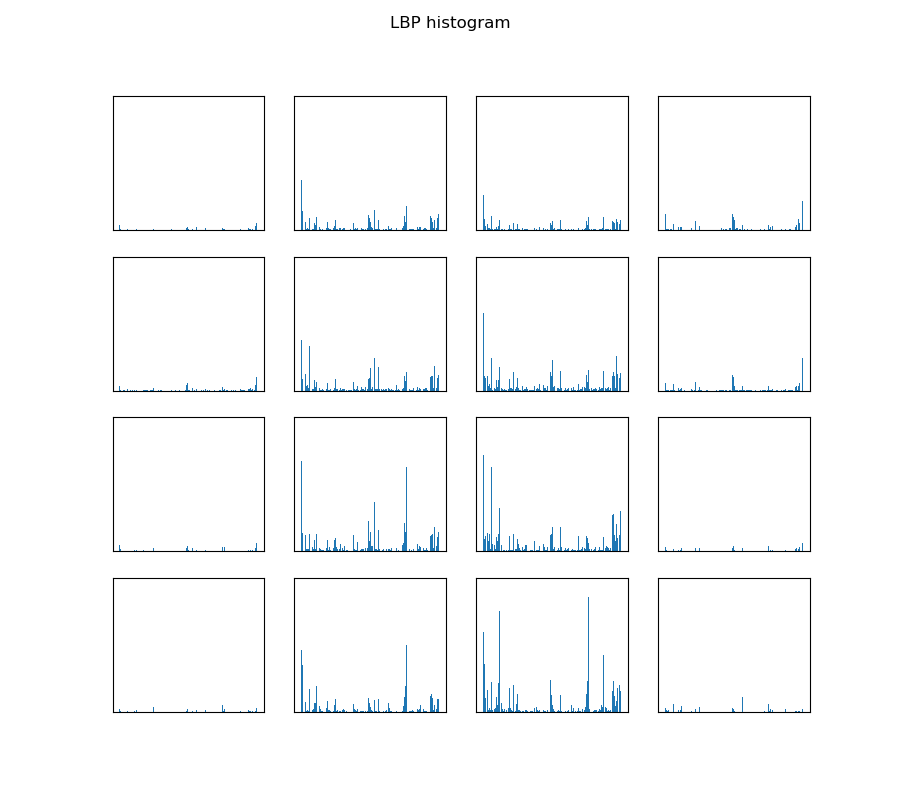
图像特征Vol.1:计算机视觉特征度量|第一弹:【纹理区域特征】
目录 一、前言二、纹理区域度量2.1:边缘特征度量2.2:互相关和自相关特征2.3:频谱方法—傅里叶谱2.4:灰度共生矩阵(GLCM)2.5:Laws纹理特征2.6:局部二值模式(LBP) 一、前言 …...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...

GruntJS-前端自动化任务运行器从入门到实战
Grunt 完全指南:从入门到实战 一、Grunt 是什么? Grunt是一个基于 Node.js 的前端自动化任务运行器,主要用于自动化执行项目开发中重复性高的任务,例如文件压缩、代码编译、语法检查、单元测试、文件合并等。通过配置简洁的任务…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...
