【线性代数/计算复杂性理论】积和式的指数时间算法:Ryser算法
文章目录
- 一、积和式的定义
- 二、Ryser算法
- 三、代码实现
一、积和式的定义
积和式(permanent)是一种和行列式长得很像的矩阵函数。在介绍积和式之前,我们先看看行列式(determinant)的定义。
首先需要引入“排列”(permutation)的概念。对于集合S={1,2,⋯,n}S=\{1,2,\cdots,n\}S={1,2,⋯,n},它的一个排列σ\sigmaσ就是对SSS中元素的一个重排。σ\sigmaσ的第iii个元素记作σi\sigma_iσi。例如,对于n=5n=5n=5,我们令σ={2,5,1,4,3}\sigma=\{2,5,1,4,3\}σ={2,5,1,4,3},则σ3=1\sigma_3=1σ3=1,σ5=3\sigma_5=3σ5=3。
排列的逆序对就是aaa在bbb前面但σa>σb\sigma_a>\sigma_bσa>σb的情况。例如σ={2,1,3,5,4}\sigma=\{2,1,3,5,4\}σ={2,1,3,5,4},有两个逆序对:(σ1,σ2)=(2,1)(\sigma_1,\sigma_2)=(2,1)(σ1,σ2)=(2,1)和(σ4,σ5)=(5,4)(\sigma_4,\sigma_5)=(5,4)(σ4,σ5)=(5,4)。一个排列σ\sigmaσ中逆序对的个数记作τ(σ)\tau(\sigma)τ(σ)。令sgn(σ)=(−1)τ(σ)\mathrm{sgn}(\sigma)=(-1)^{\tau(\sigma)}sgn(σ)=(−1)τ(σ)。对于一个排列σ\sigmaσ,如果你把其中的两个数互换,则sgn(σ)\mathrm{sgn}(\sigma)sgn(σ)会变号。所有nnn个元素的排列的集合记作SnS_nSn。例如,S3={(123),(132),(213),(231),(312),(321)}S_3=\{(1\ 2\ 3),(1\ 3\ 2),(2\ 1\ 3),(2\ 3\ 1),(3\ 1\ 2),(3\ 2\ 1)\}S3={(1 2 3),(1 3 2),(2 1 3),(2 3 1),(3 1 2),(3 2 1)}。
给定一个n×nn\times nn×n的矩阵A=(aij)n×nA=(a_{ij})_{n\times n}A=(aij)n×n,它的行列式为det(A)=∑σ∈Sn(sgn(σ)∏i=1nai,σi)\det(A)=\sum\limits_{\sigma\in S_n}\left(\mathrm{sgn}(\sigma)\prod\limits_{i=1}^{n}a_{i,\sigma_{i}}\right) det(A)=σ∈Sn∑(sgn(σ)i=1∏nai,σi)例如,当n=3n=3n=3时,设A=[abcdefghi]A=\begin{bmatrix}a&b&c\\d&e&f\\g&h&i\end{bmatrix}A=adgbehcfi,则det(A)=aei−afh+bfg−bdi+cdh−ceg\det(A)=aei-afh+bfg-bdi+cdh-ceg det(A)=aei−afh+bfg−bdi+cdh−ceg而积和式的定义就是在行列式中把sgn(σ)\mathrm{sgn}(\sigma)sgn(σ)去掉:perm(A)=∑σ∈Sn(∏i=1nai,σi)\mathrm{perm}(A)=\sum\limits_{\sigma\in S_n}\left(\prod\limits_{i=1}^{n}a_{i,\sigma_{i}}\right) perm(A)=σ∈Sn∑(i=1∏nai,σi)可以理解为:在矩阵中每行选取一个元素,且要求这些元素的列各不相同;将这些元素乘起来,得到一个乘积,积和式就是所有可能的选法对应的乘积之和。例如,当n=3n=3n=3时,设A=[abcdefghi]A=\begin{bmatrix}a&b&c\\d&e&f\\g&h&i\end{bmatrix}A=adgbehcfi,则perm(A)=aei+afh+bfg+bdi+cdh+ceg\mathrm{perm}(A)=aei+afh+bfg+bdi+cdh+ceg perm(A)=aei+afh+bfg+bdi+cdh+ceg积和式在量子场论、图论等领域中有应用。
积和式与行列式看起来只是某些项的符号不同,而且积和式看起来更简单了(没有sgn(σ)\mathrm{sgn}(\sigma)sgn(σ)),那是不是比行列式好算呢?答案是:大错特错!行列式可以用高斯消元法在O(n3)O(n^3)O(n3)的时间内算出来,而积和式目前最快的算法需要指数级的时间。事实上,1979年,Leslie G. Valiant证明了积和式的计算是#P\mathsf{\# P}#P完全问题,如果发现积和式有多项式时间的算法,那么将意味着FP=#P\mathsf{FP}=\mathsf{\#P}FP=#P,这是比P=NP\mathsf{P}=\mathsf{NP}P=NP还要强的命题。而大多数计算机科学家认为P≠NP\mathsf{P}\ne\mathsf{NP}P=NP,所以积和式大概率没有多项式时间的算法。我们要介绍的Ryser算法就是O(n2n)O(n 2^n)O(n2n)时间的。
二、Ryser算法
Ryser算法的核心思想就是容斥原理。我们还是先考察一下n=3n=3n=3的情况:令A=[abcdefghi]A=\begin{bmatrix}a&b&c\\d&e&f\\g&h&i\end{bmatrix}A=adgbehcfi,则perm(A)=aei+afh+bfg+bdi+cdh+ceg\mathrm{perm}(A)=aei+afh+bfg+bdi+cdh+ceg perm(A)=aei+afh+bfg+bdi+cdh+ceg观察式子T=(a+b+c)(d+e+f)(g+h+i)T=(a+b+c)(d+e+f)(g+h+i)T=(a+b+c)(d+e+f)(g+h+i),你会发现它的展开式中包含积和式的666个项(用蓝色标出):T=adg+adh+adi+aeg+aeh+aei+afg+afh+afi+bdg+bdh+bdi+beg+beh+bei+bfg+bfh+bfi+cdg+cdh+cdi+ceg+ceh+cei+cfg+cfh+cfi\begin{aligned} T&=a d g + a d h + a d i + a e g + a e h + \textcolor{blue}{a e i} + a f g + \textcolor{blue}{a f h} + a f i\\ &+b d g + b d h + \textcolor{blue}{b d i} + b e g + b e h + b e i + \textcolor{blue}{b f g} + b f h + b f i\\ &+c d g + \textcolor{blue}{c d h} + c d i + \textcolor{blue}{c e g} + c e h + c e i + c f g + c f h + c f i \end{aligned}T=adg+adh+adi+aeg+aeh+aei+afg+afh+afi+bdg+bdh+bdi+beg+beh+bei+bfg+bfh+bfi+cdg+cdh+cdi+ceg+ceh+cei+cfg+cfh+cfi于是,我们只需要在TTT的展开式中剔除不属于积和式的项就可以了。不属于积和式的项,也就是选取的某两个元素在同一列的项。这些项的特点是:元素的列组成的集合大小不超过222。比如adhadhadh一项,它只涉及第一和第二列,而没有涉及第三列,所以它不是积和式中的项。同样,cficficfi只涉及第三列,它也不是积和式中的项。我们可以枚举元素的列组成的集合(集合的大小为222),将对应的项剔除出去。
- 只涉及第一、二列的项:H12=(a+b)(d+e)(g+h)=adg+adh+aeg+aeh+bdg+bdh+beg+behH_{12}=(a+b)(d+e)(g+h)=a d g + a d h + a e g + a e h + b d g + b d h + b e g + b e hH12=(a+b)(d+e)(g+h)=adg+adh+aeg+aeh+bdg+bdh+beg+beh
- 只涉及第二、三列的项:H23=(b+c)(e+f)(h+i)=beh+bei+bfh+bfi+ceh+cei+cfh+cfiH_{23}=(b+c)(e+f)(h+i)=b e h + b e i + b f h + b f i + c e h + c e i + c f h + c f iH23=(b+c)(e+f)(h+i)=beh+bei+bfh+bfi+ceh+cei+cfh+cfi
- 只涉及第一、三列的项:H13=(a+c)(d+f)(g+i)=adg+adi+afg+afi+cdg+cdi+cfg+cfiH_{13}=(a+c)(d+f)(g+i)=a d g + a d i + a f g + a f i + c d g + c d i + c f g + c f iH13=(a+c)(d+f)(g+i)=adg+adi+afg+afi+cdg+cdi+cfg+cfi
只需要从TTT中把这些项剔除出去就可以了。但答案是perm(A)=T−H12−H23−H13\mathrm{perm}(A)=T-H_{12}-H_{23}-H_{13}perm(A)=T−H12−H23−H13吗?非也,因为H12H_{12}H12、H23H_{23}H23、H13H_{13}H13之间还有重叠部分,我们减的时候把重叠部分减了两次,还得加回来。H12H_{12}H12和H23H_{23}H23的重叠部分,就是只涉及第二列的项:behbehbeh。H12H_{12}H12和H13H_{13}H13的重叠部分则是只涉及第一列的项:adgadgadg。同理,H23H_{23}H23和H13H_{13}H13的重叠部分就是只涉及第三列的项——cficficfi了。
这样,我们得到计算三阶矩阵积和式的公式为:perm(A)=T−H12−H23−H13+adg+beh+cfi=(a+b+c)(d+e+f)(g+h+i)−(a+b)(d+e)(g+h)−(b+c)(e+f)(h+i)−(a+c)(d+f)(g+i)+adg+beh+cfi\begin{aligned} \mathrm{perm}(A)&=T-H_{12}-H_{23}-H_{13}+adg+beh+cfi\\ &=(a+b+c)(d+e+f)(g+h+i)-(a+b)(d+e)(g+h)-(b+c)(e+f)(h+i)-(a+c)(d+f)(g+i)+adg+beh+cfi \end{aligned}perm(A)=T−H12−H23−H13+adg+beh+cfi=(a+b+c)(d+e+f)(g+h+i)−(a+b)(d+e)(g+h)−(b+c)(e+f)(h+i)−(a+c)(d+f)(g+i)+adg+beh+cfi我们可以把这种容斥原理的思想推广到nnn阶矩阵的积和式。计算nnn阶矩阵的积和式的Ryser公式如下:perm(An×n)=(−1)n∑S⊆{1,2,⋯,n}[(−1)∣S∣∏i=1n(∑j∈Saij)]\mathrm{perm}(A_{n\times n})={(-1)}^{n} \sum\limits_{S\subseteq \{1,2,\cdots,n\}}\left[{(-1)}^{|S|}\prod\limits_{i=1}^{n}\left(\sum\limits_{j\in S}a_{ij}\right)\right] perm(An×n)=(−1)nS⊆{1,2,⋯,n}∑(−1)∣S∣i=1∏nj∈S∑aij这个公式可以这么理解:我们把AAA的行和之积展开,里面一定包含我们要求的积和式;然后减去涉及n−1n-1n−1列的项,加上涉及n−2n-2n−2列的项,减去涉及n−3n-3n−3列的项,……式中SSS就是涉及的列的集合,(−1)∣S∣(-1)^{|S|}(−1)∣S∣用于计算是加还是减;前面的(−1)n{(-1)}^{n}(−1)n是修正项,用于解决当nnn是奇数时,S={1,2,⋯,n}S=\{1,2,\cdots,n\}S={1,2,⋯,n}的情况下(−1)∣S∣{(-1)}^{|S|}(−1)∣S∣是负数的问题。
三、代码实现
理论上讲,如果我们按照格雷码顺序枚举SSS,那么时间复杂度可以降到O(n2n)O(n2^n)O(n2n)。但在这里我们为了方便起见就递归枚举SSS,对于每个SSS,计算各行的、列号为SSS的元素之和的乘积即可。下面给出一个时间复杂度为O(n22n)O(n^2 2^n)O(n22n)的C++实现:
#include <cstdint>typedef std::int64_t num;num recursion(int i, bool* b, int n, num** A)// 枚举S
{if(i == n) // 递归终点,已经得到一个S{num prod = 1;for(int row = 0; row < n; row++){num sum = 0;for(int col = 0; col < n; col++){if(b[col]){sum += A[row][col];}}prod *= sum;}int S_size = 0; // |S|for(int col = 0; col < n; col++){if(b[col]){S_size++;}}if(S_size % 2 == 1) // (-1)^|S|{prod = -prod;}return prod;}num result = 0;b[i] = true; // 选第i列result += recursion(i + 1, b, n, A);b[i] = false; // 不选第i列result += recursion(i + 1, b, n, A);return result;
}num ryser(int n, num** A)// 计算n x n矩阵A的积和式
{bool* b = new bool[n]; // S中是否含有第i列num result = recursion(0, b, n, A);delete []b;if(n % 2 == 1){result = -result; // (-1)^n}return result;
}
相关文章:

【线性代数/计算复杂性理论】积和式的指数时间算法:Ryser算法
文章目录一、积和式的定义二、Ryser算法三、代码实现一、积和式的定义 积和式(permanent)是一种和行列式长得很像的矩阵函数。在介绍积和式之前,我们先看看行列式(determinant)的定义。 首先需要引入“排列”&#x…...

代码随想录 NO52 | 动态规划_leetcode 647. 回文子串 516.最长回文子序列
动态规划_leetcode 647. 回文子串 516.最长回文子序列今天是动态规划最后一天的题了,整个过程已经接近尾声了! 647. 回文子串 确定dp数组(dp table)以及下标的含义 本题如果我们定义,dp[i] 为 下标i结尾的字符串有 dp…...
【数据挖掘】1、综述:背景、数据的特征、数据挖掘的六大应用方向、有趣的案例
目录一、背景1.1 学习资料1.2 数据的特征1.3 数据挖掘的应用案例1.4 获取数据集1.5 数据挖掘的定义二、分类三、聚类四、关联分析五、回归六、可视化七、数据预处理八、有趣的案例8.1 隐私保护8.2 云计算的弹性资源8.3 并行计算九、总结一、背景 1.1 学习资料 推荐书籍如下&a…...
【架构师】零基础到精通——康威定律
博客昵称:架构师Cool 最喜欢的座右铭:一以贯之的努力,不得懈怠的人生。 作者简介:一名Coder,软件设计师/鸿蒙高级工程师认证,在备战高级架构师/系统分析师,欢迎关注小弟! 博主小留言…...

Could not extract response: no suitable HttpMessageConverter
版本:spring-cloud-openfeign-core-2.1.1.RELEASE.jar,spring-webmvc-5.1.14.RELEASE.jar,jetty-server-9.4.41.v20210516.jar,tomcat-embed-core-9.0.48.jar 问题背景 生产服务请求下游服务时偶发抛出下面的异常,下…...

文献计量三大定律之一---洛特卡定律及普赖斯定律
科学生产率是洛特卡定律的基础,科学生产率”(Scientific Productivity))是指科学家(科研人员)在科学上所表现出的能力和工作效率,通常用其生产的科学文献的数量来衡量。 1926年,洛特卡在一篇论文中提出了科…...
2023年软考高级网络规划设计师
网络规划设计师是软考高级考试科目之一,也是比较难的科目,据官方数据统计网规每年的通过率很低,而且每年只有下半年11月份考一次,如果是直接裸考,估计很悬哦~ 但是你参加考试获得证书的过程就是一个学习网络规划系统知…...

数据治理驱动因素 -报考题
数据治理并不是到此为止,而是需要直接与企业战略保持一致。数据治理越显著地帮助解决组织问题,人们越有可能改变行为、接受数据治理实践。数据治理的驱动因素大多聚焦于减少风险或者改进流程。(1)减少风险1)一般性风险…...
2023淘宝天猫38节红包满减优惠活动时间是从几月几号什么时候开始?
2023年淘宝天猫38节活动将于2023年3月2日中午12点正式开始,活动将持续至2023年3月8日晚上23点59分。届时,淘宝天猫将推出一系列的优惠活动和红包福利,为广大女性用户送上节日的祝福和福利。在这个特别的节日里,淘宝天猫为女性用户…...
、数据压缩、存储优化)
Hive表优化、表设计优化、Hive表数据优化(ORC)、数据压缩、存储优化
文章目录Hive表优化Hive表设计优化分区表结构 - 分区设计思想分桶表结构 - Join问题Hive中的索引Hive表数据优化常见文件格式TextFileSequenceFileParquetORC数据压缩存储优化 - 避免小文件生成存储优化 - 合并输入的小文件存储优化 - ORC文件索引Row Group IndexBloom Filter …...

LearnOpenGL-入门-着色器
本人刚学OpenGL不久且自学,文中定有代码、术语等错误,欢迎指正 我写的项目地址:https://github.com/liujianjie/LearnOpenGLProject LearnOpenGL中文官网:https://learnopengl-cn.github.io/ 文章目录着色器GLSL数据类型输入与输…...
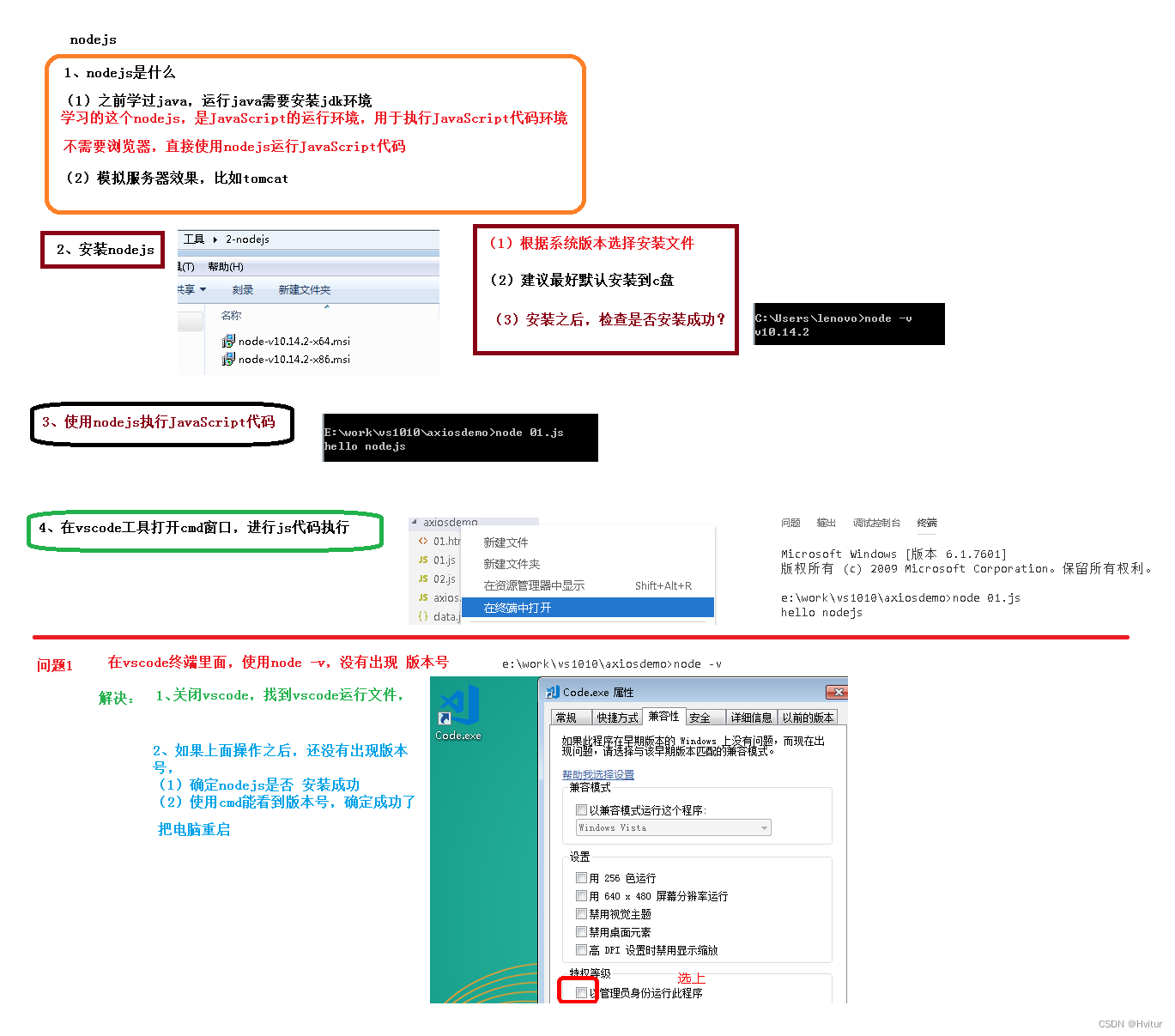
【谷粒学院】vue、axios、element-ui、node.js(44~58)
44.前端技术-vue入门 🧨Vue.js 是什么 Vue (读音 /vjuː/,类似于 view) 是一套用于构建用户界面的渐进式框架。 Vue 的核心库只关注视图层,不仅易于上手,还便于与第三方库或既有项目整合。另一方面,当与现代化的工具…...

【一些回忆】2022.02.26-2023.02.26 一个普通男孩的365天
💃🏼 本人简介:男 👶🏼 年龄:18 🤞 作者:那就叫我亮亮叭 📕 专栏:一些回忆 为什么选择在这个时间节点回忆一下呢? 一是因为今天距离2023高考仅剩1…...
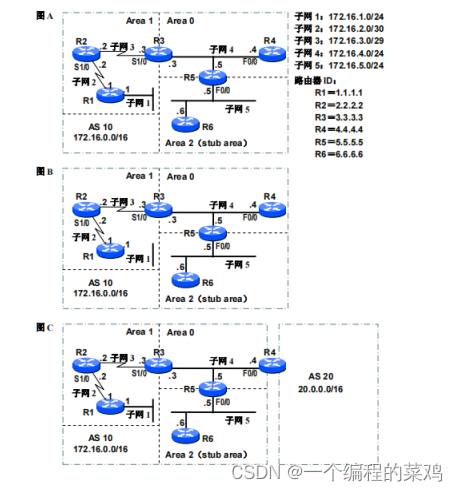
OSPF的多区域特性 (电子科技大学TCP/IP实验三)
一.实验目的 1、掌握OSPF 协议中区域的类型、特征和作用 2、掌握OSPF 路由器的类型、特征和作用 3、掌握OSPF LSA 分组的类型、特征和作用 4、理解OSPF 区域类型、路由器类型和OSPF LSA 分组类型间的相互关系 二.预备知识 1、静态路由选择和动态路…...
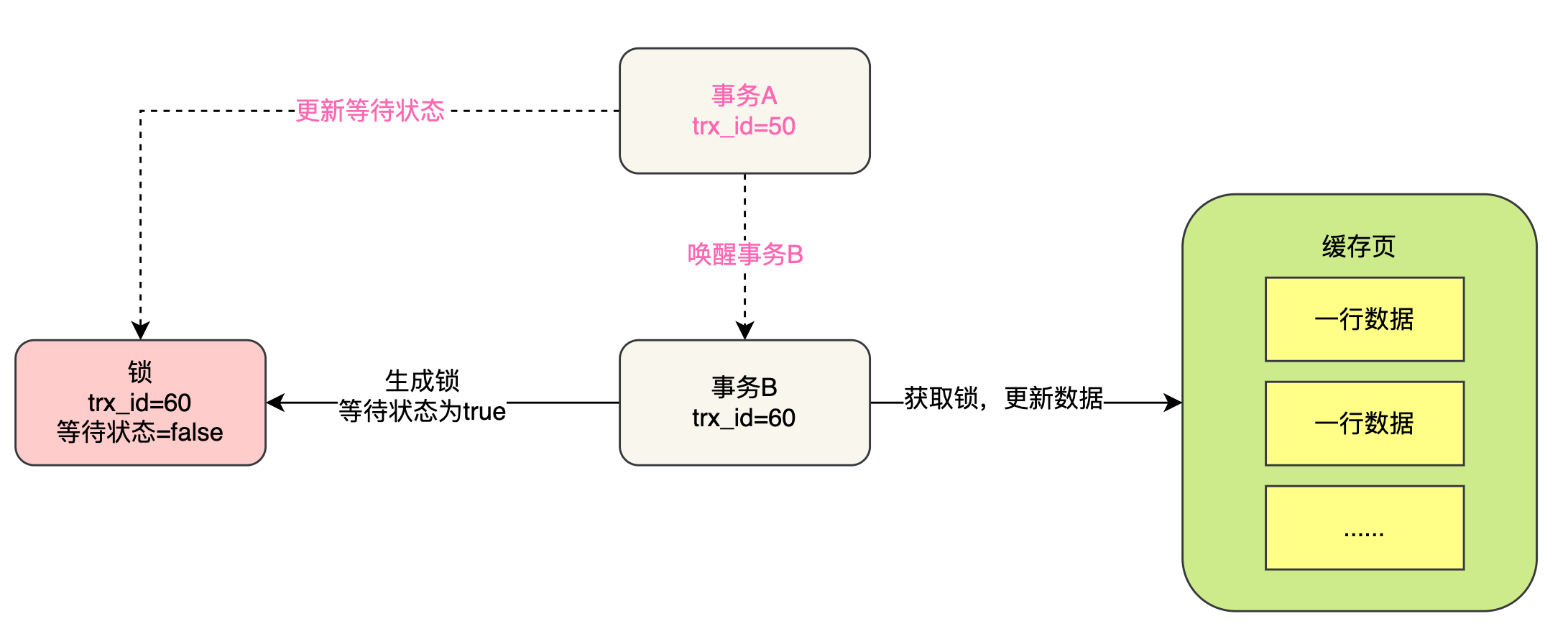
(四十四)多个事务更新同一行数据时,是如何加锁避免脏写的?
之前我们已经用很多篇幅给大家讲解了多个事务并发运行的时候,如果同时要读写一批数据,此时读和写时间的关系是如何协调的,毕竟要是你不协调好的话,可能就会有脏读、不可重复读、幻读等一系列的问题。 简单来说,脏读、…...

【数据库】第十二章 数据库管理
第12章 数据库管理 数据库的物理存储 关于内存、外存、磁盘、硬盘、软盘、光盘的区别_Allenzyg的博客-CSDN博客_磁盘和硬盘的区别 数据库记录在磁盘上的存储 定长,变长跨块,非跨快 文件的组织方方法: 无序记录文件(堆文件heap或pile file…...
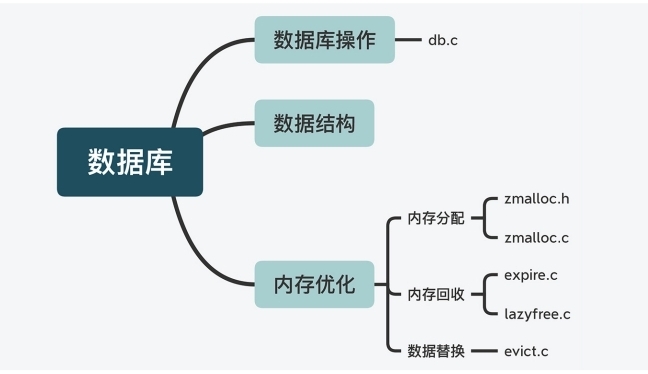
Redis源码---整体架构
目录 前言 Redis目录结构 前言 deps目录 src 目录 tests 目录 utils 目录 重要的配置文件 Redis 功能模块与源码对应 前言 服务器实例 数据库数据类型与操作 高可靠性和高可扩展性 辅助功能 前言 以先面后点的方法推进无特殊说明,都是基于 Redis 5.0.…...
基于springboot+vue的校园招聘系统
博主主页:猫头鹰源码 博主简介:Java领域优质创作者、CSDN博客专家、公司架构师、全网粉丝5万、专注Java技术领域和毕业设计项目实战 主要内容:毕业设计(Javaweb项目|小程序等)、简历模板、学习资料、面试题库、技术咨询 文末联系获取 项目介绍…...
SAP MM学习笔记1-SAP中扩张的概念,如何将一个物料从工厂A扩张到工厂B
MM中在创建物料的时候,最低也得创建如下5个view。 基本数据1 基本数据2 购买管理 会计1 会计2 1,扩张是什么 有时候,你想增加其他的View,比如保管场所 等,你不能用MM02来做编辑,要用MM01来做扩张。这就是扩…...
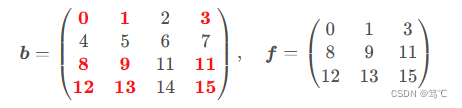
【Python】Numpy数组的切片、索引详解:取数组的特定行列
【Python】Numpy数组的切片、索引详解:取数组的特定行列 文章目录【Python】Numpy数组的切片、索引详解:取数组的特定行列1. 介绍2. 切片索引2.1 切片索引先验知识2.1 一维数组的切片索引2.3 多维数组的切片索引3. 数组索引(副本)…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...

LangChain知识库管理后端接口:数据库操作详解—— 构建本地知识库系统的基础《二》
这段 Python 代码是一个完整的 知识库数据库操作模块,用于对本地知识库系统中的知识库进行增删改查(CRUD)操作。它基于 SQLAlchemy ORM 框架 和一个自定义的装饰器 with_session 实现数据库会话管理。 📘 一、整体功能概述 该模块…...

STM32---外部32.768K晶振(LSE)无法起振问题
晶振是否起振主要就检查两个1、晶振与MCU是否兼容;2、晶振的负载电容是否匹配 目录 一、判断晶振与MCU是否兼容 二、判断负载电容是否匹配 1. 晶振负载电容(CL)与匹配电容(CL1、CL2)的关系 2. 如何选择 CL1 和 CL…...

日常一水C
多态 言简意赅:就是一个对象面对同一事件时做出的不同反应 而之前的继承中说过,当子类和父类的函数名相同时,会隐藏父类的同名函数转而调用子类的同名函数,如果要调用父类的同名函数,那么就需要对父类进行引用&#…...
