Codeforces Round#853 div2 A-C
Codeforces Round#853 div2 A-C
等了很久终于迎来了一场cf比赛,白天出去玩了一圈,晚上回来打比赛,这次只出了A,B题。C题思路很巧妙,赛时没做出来,看了大佬学习到了,还是很不错。
A.Serval and Mocha’s Array 签到
题意:这个题题目有点绕,看了十分钟才明白意思,就是给你一个数组,判断能否重新排列数组使得数组前两项的最大公约数是否小于等于2。
思路:数据范围小,直接暴力枚举判断即可。
void Showball(){int n;cin>>n;vector<int> a(n);for(int i=0;i<n;i++) cin>>a[i];int ok=0;for(int i=0;i<n;i++){for(int j=i+1;j<n;j++){int g=gcd(a[i],a[j]);if(g<=2) {ok=1;break;}}}if(ok) cout<<"YES"<<endl;else cout<<"NO"<<endl;
}
B. Serval and Inversion Magic
题意:给你一个只含0和1的字符串,给你一个操作,可以将区间[L,R]之间的字符0变成1,1变成0。问你能否通过一次操作,将字符串变成回文串。
思路:因为我们只能够操作一段连续的区间。我们可以对比回文串对应的字符s[i]s[i]s[i]和s[n−i−1]s[n-i-1]s[n−i−1]如果出现不相同,又相同,又不相同的情况,那么两端区间都需要操作,但是不连续,那么我们无法满足题意。所以进行标记判断这种情况即可。
void Showball(){string s,t;int n;cin>>n;cin>>s;if(s==t) {cout<<"YES"<<endl;return;}int ok=1;bool f1=false,f2=false;for(int i=0;i<n/2;i++){if(s[i]!=s[n-i-1]) f1=true;if(f1&&s[i]==s[n-i-1]) f2=true;if(f2&&s[i]!=s[n-i-1]) {ok=0;break;}}if(ok) cout<<"YES"<<endl;else cout<<"NO"<<endl;
}
C. Serval and Toxel’s Arrays 思维
题意:给你一个数组AiA_iAi,并且进行m次操作,每次操作都会将上一个数组中的第p个元素修改为v。得到新的数组。然后我们需要统计
所有AiA_iAi和AjA_jAj数组之间不同元素个数之和。
思路:如果我们直接进行模拟,在暴力计算,无疑会超时。那么遇到这种题目我们就需要算贡献,算贡献是一种计数类问题的经典套路。对于本题,我们可以算出每个数对答案的贡献,我们知道一共会有m+1m+1m+1个数组,对于数xxx,我们假设它在这m+1m+1m+1个数组中出现的次数为cnt,那么就可以分为两种情况,第一种情况,计算的两个数组中都含x,那么x对答案的贡献是1,这种情况一共有Ccnt2=cnt∗(cnt−1)/2C_{cnt}^2=cnt*(cnt-1)/2Ccnt2=cnt∗(cnt−1)/2种情况,对于计算的两个数组,一个含x另外一个不含x,那么他的贡献也是1,这种情况一种有cnt∗(m−cnt+1)cnt*(m-cnt+1)cnt∗(m−cnt+1)种,对于计算的两个数组都不含x的情况,那么x没有贡献,则不用计算。
所以我们现在就只需要计算出每个数在所有数组中出现的次数,以及在每次操作时维护好这个次数即可。
我们可以开一个map去记录每个数出现的次数,一个比较好的思路就是一开始我们假定后面每个数都没有改变,那么每个数出现的次数都是m+1m+1m+1次,那么在第i次操作时,将a[p]a[p]a[p]变为了vvv,那么a[p]a[p]a[p]的次数就会减少,减少了多少呢,很明显在这次操作之后的数组中都暂时不在含有a[p]a[p]a[p],也就是m−i+1m-i+1m−i+1个。所以mp[a[p]]−=(m−i+1)mp[a[p]]-=(m-i+1)mp[a[p]]−=(m−i+1),同理vvv这个数出现的次数自然就暂时增加了这么多。
最后带入公式计算即可,注意开long long。
void Showball(){int n,m;cin>>n>>m;vector<int> a(n);map<int,LL> mp;for(auto &it:a){cin>>it;mp[it]=m+1ll;}for(int i=1;i<=m;i++){int p,v;cin>>p>>v;mp[a[--p]]-=m-i+1;mp[v]+=m-i+1;a[p]=v;}LL ans=0;for(auto &[k,v]:mp){ans+=v*(v-1)/2ll+(m-v+1)*v;}cout<<ans<<endl;
}
相关文章:

Codeforces Round#853 div2 A-C
Codeforces Round#853 div2 A-C 等了很久终于迎来了一场cf比赛,白天出去玩了一圈,晚上回来打比赛,这次只出了A,B题。C题思路很巧妙,赛时没做出来,看了大佬学习到了,还是很不错。 A.Serval and Mocha’s A…...
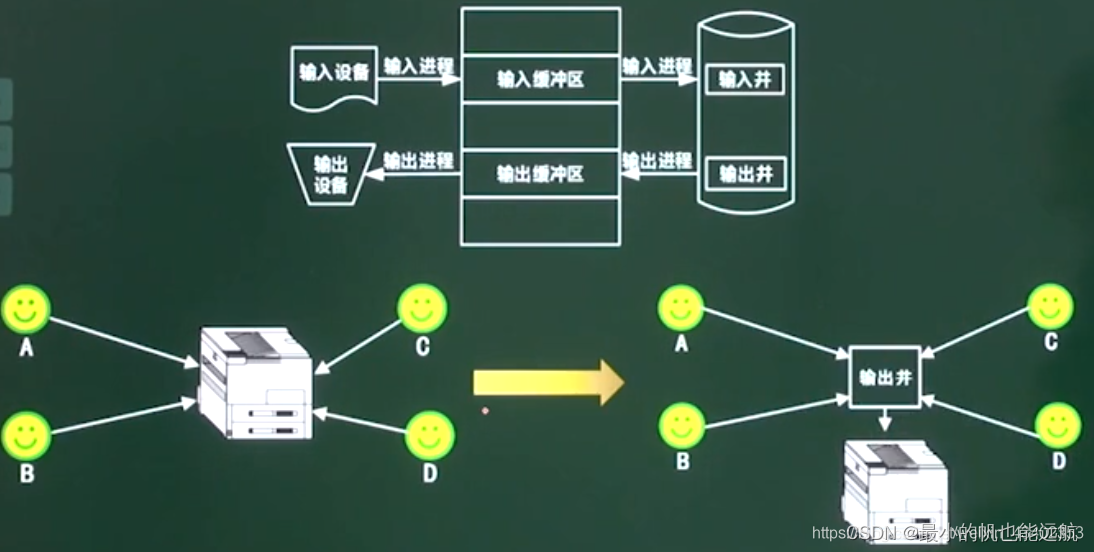
软考之操作系统知识
目录 1.进程管理-进程的概念 2.进程的三态图和五态图 3.进程的同步与互斥 4.PV操作应用 5.死锁问题 6.银行家算法 7.存储管理 8.段式存储组织 9.段页式存储组织 10.页面置换算法 11.磁盘管理 12.作业管理 13.索引文件结构 14.树型目录结构 15.空闲存储空间管理 …...

【线性代数/计算复杂性理论】积和式的指数时间算法:Ryser算法
文章目录一、积和式的定义二、Ryser算法三、代码实现一、积和式的定义 积和式(permanent)是一种和行列式长得很像的矩阵函数。在介绍积和式之前,我们先看看行列式(determinant)的定义。 首先需要引入“排列”&#x…...

代码随想录 NO52 | 动态规划_leetcode 647. 回文子串 516.最长回文子序列
动态规划_leetcode 647. 回文子串 516.最长回文子序列今天是动态规划最后一天的题了,整个过程已经接近尾声了! 647. 回文子串 确定dp数组(dp table)以及下标的含义 本题如果我们定义,dp[i] 为 下标i结尾的字符串有 dp…...
【数据挖掘】1、综述:背景、数据的特征、数据挖掘的六大应用方向、有趣的案例
目录一、背景1.1 学习资料1.2 数据的特征1.3 数据挖掘的应用案例1.4 获取数据集1.5 数据挖掘的定义二、分类三、聚类四、关联分析五、回归六、可视化七、数据预处理八、有趣的案例8.1 隐私保护8.2 云计算的弹性资源8.3 并行计算九、总结一、背景 1.1 学习资料 推荐书籍如下&a…...
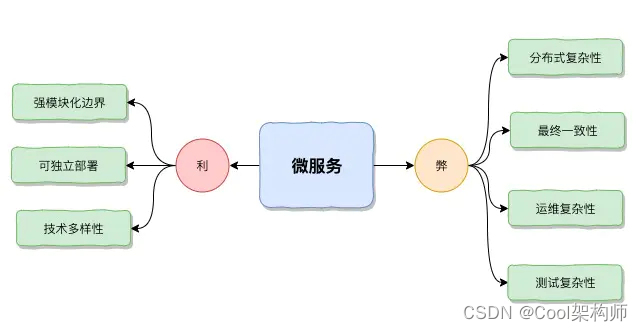
【架构师】零基础到精通——康威定律
博客昵称:架构师Cool 最喜欢的座右铭:一以贯之的努力,不得懈怠的人生。 作者简介:一名Coder,软件设计师/鸿蒙高级工程师认证,在备战高级架构师/系统分析师,欢迎关注小弟! 博主小留言…...

Could not extract response: no suitable HttpMessageConverter
版本:spring-cloud-openfeign-core-2.1.1.RELEASE.jar,spring-webmvc-5.1.14.RELEASE.jar,jetty-server-9.4.41.v20210516.jar,tomcat-embed-core-9.0.48.jar 问题背景 生产服务请求下游服务时偶发抛出下面的异常,下…...

文献计量三大定律之一---洛特卡定律及普赖斯定律
科学生产率是洛特卡定律的基础,科学生产率”(Scientific Productivity))是指科学家(科研人员)在科学上所表现出的能力和工作效率,通常用其生产的科学文献的数量来衡量。 1926年,洛特卡在一篇论文中提出了科…...
2023年软考高级网络规划设计师
网络规划设计师是软考高级考试科目之一,也是比较难的科目,据官方数据统计网规每年的通过率很低,而且每年只有下半年11月份考一次,如果是直接裸考,估计很悬哦~ 但是你参加考试获得证书的过程就是一个学习网络规划系统知…...

数据治理驱动因素 -报考题
数据治理并不是到此为止,而是需要直接与企业战略保持一致。数据治理越显著地帮助解决组织问题,人们越有可能改变行为、接受数据治理实践。数据治理的驱动因素大多聚焦于减少风险或者改进流程。(1)减少风险1)一般性风险…...
2023淘宝天猫38节红包满减优惠活动时间是从几月几号什么时候开始?
2023年淘宝天猫38节活动将于2023年3月2日中午12点正式开始,活动将持续至2023年3月8日晚上23点59分。届时,淘宝天猫将推出一系列的优惠活动和红包福利,为广大女性用户送上节日的祝福和福利。在这个特别的节日里,淘宝天猫为女性用户…...
、数据压缩、存储优化)
Hive表优化、表设计优化、Hive表数据优化(ORC)、数据压缩、存储优化
文章目录Hive表优化Hive表设计优化分区表结构 - 分区设计思想分桶表结构 - Join问题Hive中的索引Hive表数据优化常见文件格式TextFileSequenceFileParquetORC数据压缩存储优化 - 避免小文件生成存储优化 - 合并输入的小文件存储优化 - ORC文件索引Row Group IndexBloom Filter …...

LearnOpenGL-入门-着色器
本人刚学OpenGL不久且自学,文中定有代码、术语等错误,欢迎指正 我写的项目地址:https://github.com/liujianjie/LearnOpenGLProject LearnOpenGL中文官网:https://learnopengl-cn.github.io/ 文章目录着色器GLSL数据类型输入与输…...
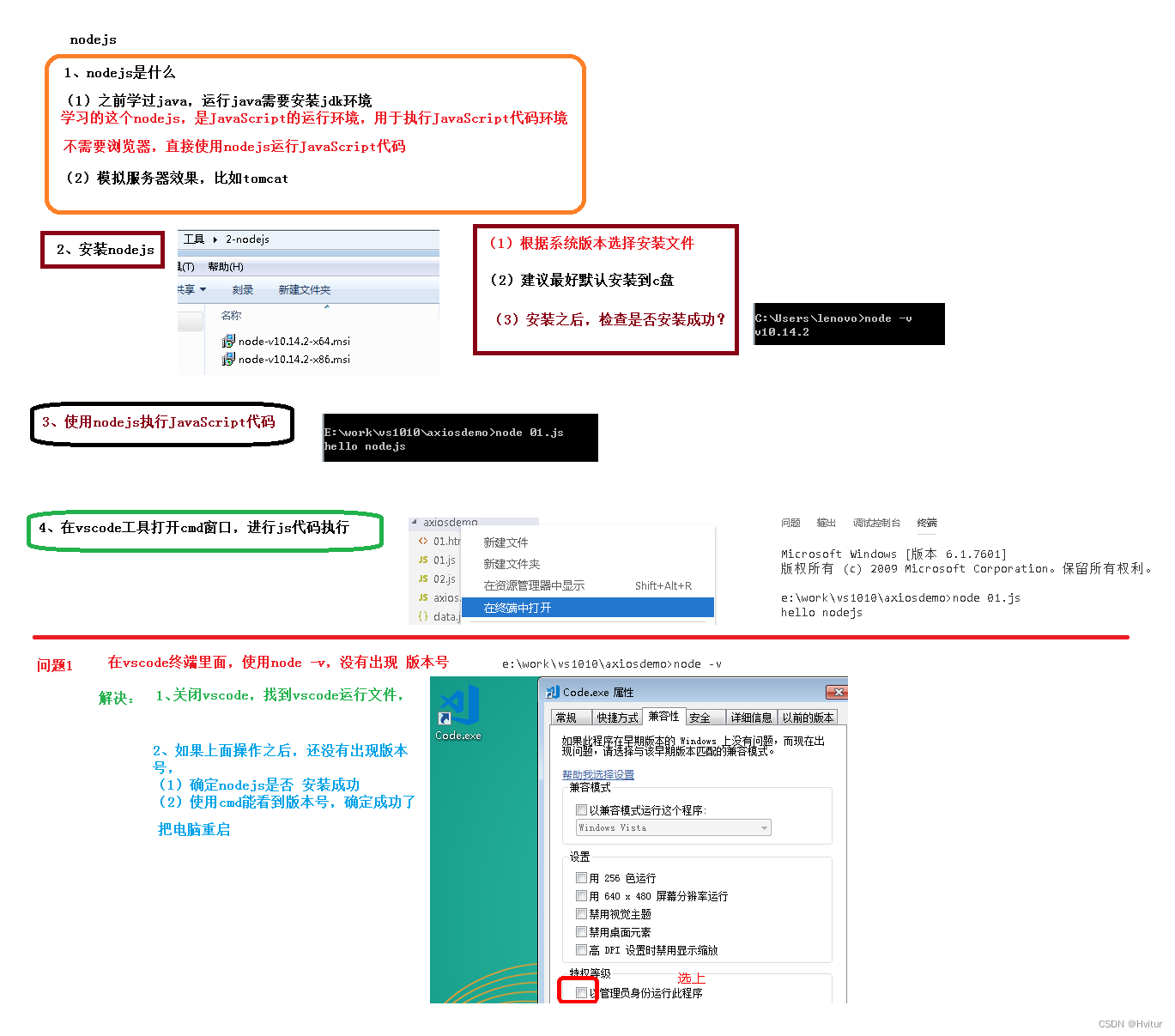
【谷粒学院】vue、axios、element-ui、node.js(44~58)
44.前端技术-vue入门 🧨Vue.js 是什么 Vue (读音 /vjuː/,类似于 view) 是一套用于构建用户界面的渐进式框架。 Vue 的核心库只关注视图层,不仅易于上手,还便于与第三方库或既有项目整合。另一方面,当与现代化的工具…...

【一些回忆】2022.02.26-2023.02.26 一个普通男孩的365天
💃🏼 本人简介:男 👶🏼 年龄:18 🤞 作者:那就叫我亮亮叭 📕 专栏:一些回忆 为什么选择在这个时间节点回忆一下呢? 一是因为今天距离2023高考仅剩1…...
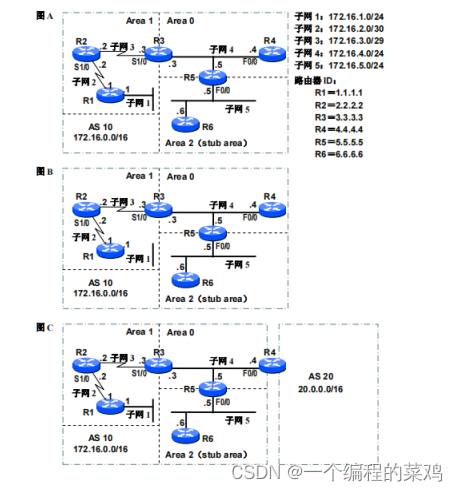
OSPF的多区域特性 (电子科技大学TCP/IP实验三)
一.实验目的 1、掌握OSPF 协议中区域的类型、特征和作用 2、掌握OSPF 路由器的类型、特征和作用 3、掌握OSPF LSA 分组的类型、特征和作用 4、理解OSPF 区域类型、路由器类型和OSPF LSA 分组类型间的相互关系 二.预备知识 1、静态路由选择和动态路…...
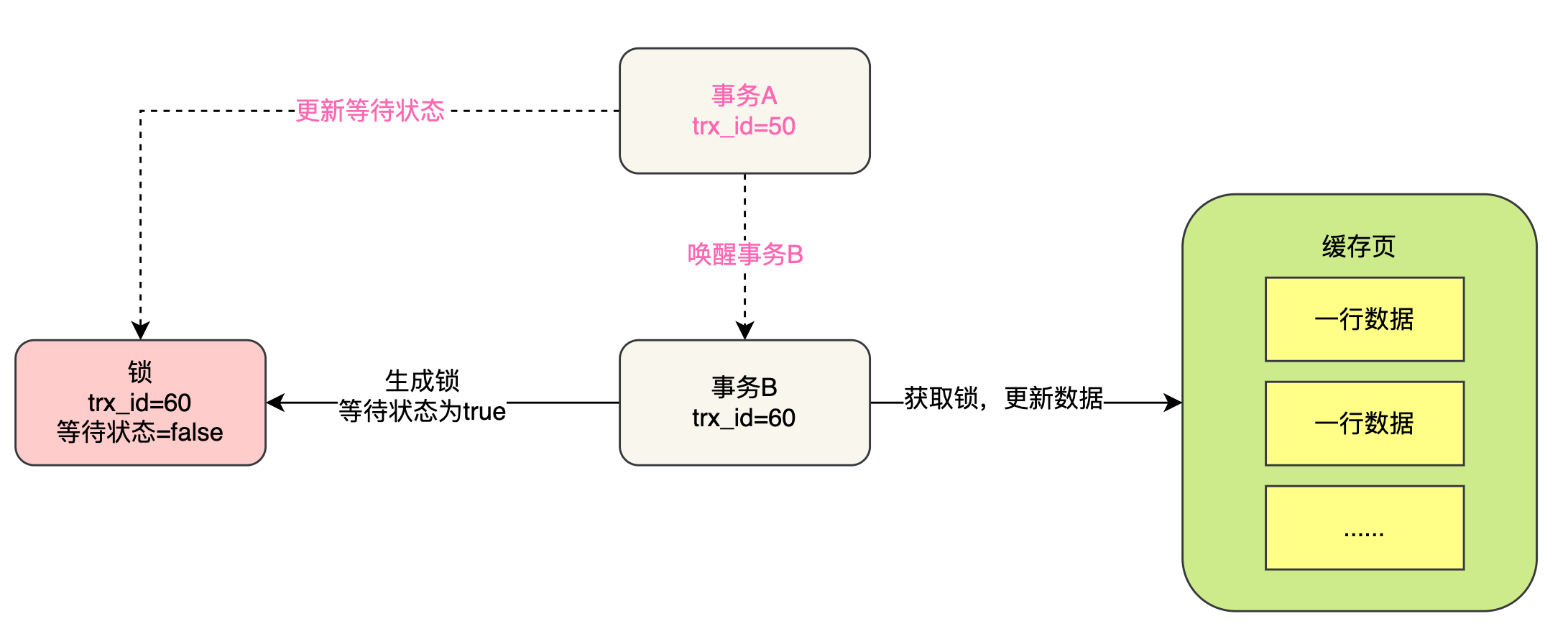
(四十四)多个事务更新同一行数据时,是如何加锁避免脏写的?
之前我们已经用很多篇幅给大家讲解了多个事务并发运行的时候,如果同时要读写一批数据,此时读和写时间的关系是如何协调的,毕竟要是你不协调好的话,可能就会有脏读、不可重复读、幻读等一系列的问题。 简单来说,脏读、…...

【数据库】第十二章 数据库管理
第12章 数据库管理 数据库的物理存储 关于内存、外存、磁盘、硬盘、软盘、光盘的区别_Allenzyg的博客-CSDN博客_磁盘和硬盘的区别 数据库记录在磁盘上的存储 定长,变长跨块,非跨快 文件的组织方方法: 无序记录文件(堆文件heap或pile file…...
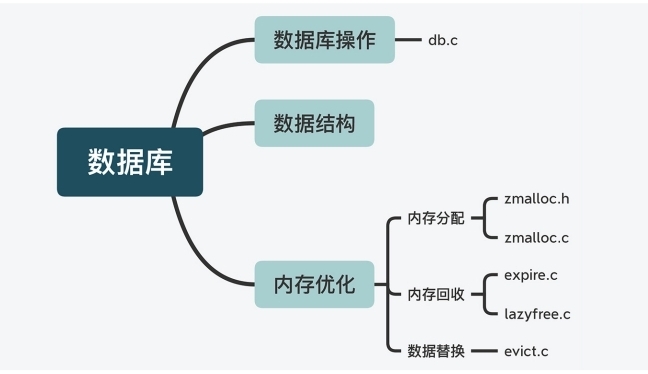
Redis源码---整体架构
目录 前言 Redis目录结构 前言 deps目录 src 目录 tests 目录 utils 目录 重要的配置文件 Redis 功能模块与源码对应 前言 服务器实例 数据库数据类型与操作 高可靠性和高可扩展性 辅助功能 前言 以先面后点的方法推进无特殊说明,都是基于 Redis 5.0.…...
基于springboot+vue的校园招聘系统
博主主页:猫头鹰源码 博主简介:Java领域优质创作者、CSDN博客专家、公司架构师、全网粉丝5万、专注Java技术领域和毕业设计项目实战 主要内容:毕业设计(Javaweb项目|小程序等)、简历模板、学习资料、面试题库、技术咨询 文末联系获取 项目介绍…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...
