CTF-Crypto学习记录-第四天 “ “ --- SHA1安全散列算法,实现原理。
文章目录
- 前言
- SHA-1加密算法介绍
- 关于SHA-1和MD5
- SHA-1 加密过程
- 原文处理
- 设置初始值和数据结构定义
- 加密运算原理过程
- 在python中调用SHA-1
前言
MD5学习MD5加密算法
SHA-1加密算法介绍
SHA-1(Secure Hash Algorithm1,安全散列算法1)是一种密码散列函数。
SHA-1可以生成一个被称为消息摘要的160位(20字节)散列值,散列值通常的呈现形式为40个十六进制数。
SHA-1的历史:
2005年,密码分析人员发现了对SHA-1的有效攻击方法,这表明该算法可能不够安全,不能继续使用,自2010年以来,许多组织建议用SHA-2或SHA-3来替换SHA-1。Microsoft、Google以及Mozilla都宣布,它们旗下的浏览器将在2017年停止接受使用SHA-1算法签名的SSL证书。
2017年2月23日,CWI Amsterdam与Google宣布了一个成功的SHA-1碰撞攻击,发布了两份内容不同但SHA-1散列值相同的PDF文件作为概念证明。
2020年,针对SHA-1的选择前缀冲突攻击已经实际可行。建议尽可能用SHA-2或SHA-3取代SHA-1。
关于SHA-1和MD5
在上一篇学习笔记里学了MD5加密算法,SHA-1和MD5同样是哈希函数,俩者对于任意长度明文的预处理也都是相同的,那么俩者有什么不同呢?
- 摘要长度 (安全性)
SHA-1所产生的摘要是160位比MD5产生的摘要长32位,因此在安全性上SHA-1高于MD5。 - 运算速度
同样因为,SHA-1的摘要长于MD5,运算步骤也比MD5多了16步,因此运算速度要慢于MD5
关于MD5和SHA-1,在如今现代计算环境中都已经不再被认为是安全的哈希函数了,为了保证数据和应用的安全,应该使用SHA-256或SHA-3等算法。
SHA-1 加密过程
同MD5一样,可以分为三个过程:
原文处理
对于任意长度明文,需要先进行填充处理,使得明文长度为448(mod 512)位,有俩种情况:
- 原始明文长度mod512不为448,需要进行填充;这里假设原始明文一共有b bit,那就在b+1 bit处填充一个1,后面全部填充0,直到明文长度mod512等于448为止。
- 第二种情况,原始明文长度mod512正好为448,这种情况也需要进行填充,总共填充512位的数据,直到明文再次mod512等于448为止。
因此填充的数据长度最小为1 bit ,最大为512 bit。‘
’
再得到448bit长度的明文后,还需要添加64bit的数据,使得明文长度等于512 bit。
填充处理完成之后是分组处理:
要先将恰好为512整数倍的明文,分成 L 个512 bit长度 的明文分组。接下来对每个512 bit大小的明文分组进行类似于MD5的操作;
- 先将512 bit 的明文分组,分成 16个 32 bit的子明文分组。可以用 M[k] 表示
- 之后再将这16个子明文分组扩展到 80个子明文分组。 可以用W[k]表示
扩充的方式如下:
W t = M t , 当0≤t≤15
W t = ( W t-3 ⊕ W t-8⊕ W t-14⊕ W t-16 ) <<< 1, 当16≤t≤79
设置初始值和数据结构定义
一些相关定义:
SHA 1 针对输入的比特流是按块 (block) 依次进行处理的, 每个块的长度固定为 512 bit, SHA 1 算法允许的最大输入长度为 2^64−1 bit, 在 SHA 1 算法中, 我们将 32 bit 定义为字 (word), 所以每个字可以用 8 位十六进制来表示, 例如对于字 1010 0001 0000 0011 1111 1110 0010 0011 可表示为 A103FE23, 对于一个长度在 [0, 2^32−1] 的整数便可以用一个字来表示, 整数的最低有效 4 位为字的最右侧的十六进制字符, 对于一个整数 z, 若 0≤z<2^64 则 z=(2^32*x+y), 其中 0≤x,y<2^32, 于是 x, y都分别可以用一个字来表示, 我们记这两个字分别为 X, Y, 此时整数 z 便可以使用这对字来表示, 我们记为 (X,Y)
可以将针对bit 的逻辑运算符扩展定义到字上;
X AND Y 为两个字按位逻辑与
X OR Y 为两个字按位逻辑或
X XOR Y 为两个字按位异或
NOT X 为对字 X 的每一位按位取反
除了逻辑运算符,还可以定义字上的算术运算,
X + Y 定义为 (x + y) mod 2^32
最后定义字上的循环左移运算符(逻辑移位),循环左移即是将字的比特整体向左移动 n 位, 左侧溢出的比特位补到右侧空出来的比特位, 我们将这一运算记作 S^n(X), 循环左移可以使用逻辑表达式来描述, 如下所示:
S^n(X) = (X << n) OR (X >> 32 -n)
MD5中有4个初始变量值,而SHA-1中有五个链接变量,如下:
H0=0x67452301H1=0xEFCDAB89H2=0x98BADCFEH3=0x10325476H4=0xC3D2E1F0
此外 SHA-1定义了4个逻辑函数和4个常量。每个逻辑函数针对3个字作为输入,函数的输出为一个字,其中 t (0 ≤ t ≤ 79) 是变量, 函数的表达式如下:
f(t;B,C,D) = (B AND C) OR ((NOT B) AND D) ( 0 <= t <= 19)f(t;B,C,D) = B XOR C XOR D (20 <= t <= 39)f(t;B,C,D) = (B AND C) OR (B AND D) OR (C AND D) (40 <= t <= 59)f(t;B,C,D) = B XOR C XOR D (60 <= t <= 79)
4个常量分别如下(十六进制表示):
K(t) = 5A827999 ( 0 <= t <= 19)K(t) = 6ED9EBA1 (20 <= t <= 39)K(t) = 8F1BBCDC (40 <= t <= 59)K(t) = CA62C1D6 (60 <= t <= 79)
加密运算原理过程
SHA1有4轮运算,每一轮包括20个步骤,一共80步。
下图是 SHA-1算法中的一个回圈;
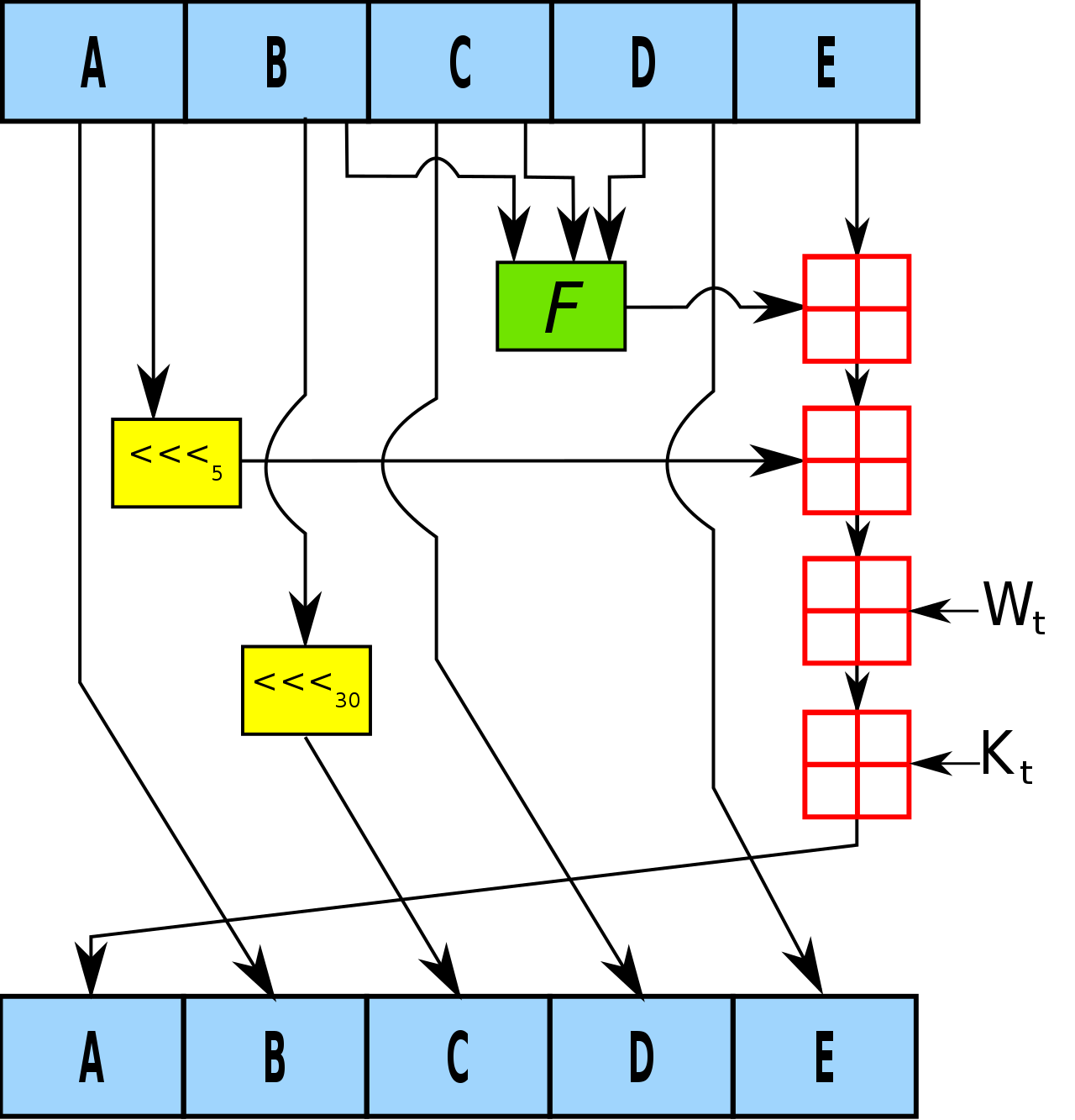
- 也如MD5一样,SHA-1会现将H0,H1,H2,H3,H4,H5五个初始变量依次放入ABCDE中;即 A = H0, B = H1, C = H2, D = H3, E = H4
- 定义循环变量 t, 对 t 从 0 到 79 依次赋值, 每一次循环执行如下操作:
- TEMP = S^5(A) + f(t;B,C,D) + E + W(t) + K(t);
- E = D;
- D = C;
- C = S^30(B);
- B = A;
- A = TEMP;
- 分别令 H0 = H0 + A, H1 = H1 + B, H2 = H2 + C, H3 = H3 + D, H4 = H4 + E
从 M(0) 开始每一轮计算后会得到新的 H0, H1, … , H4, 下一轮计算中使用上一次产生的新值, 对最后一个块计算完毕后得到的 H0, H1, … , H4便是算法的输出, 即原文的 SHA 1 哈希值
在python中调用SHA-1
import hashlib# 要哈希的数据
data = b'Hello, World!' # 在 Python 3 中,请确保数据以字节字符串的形式表示# 创建一个 SHA-1 哈希对象
sha1 = hashlib.sha1()# 更新哈希对象以处理数据
sha1.update(data)# 获取 SHA-1 哈希值的十六进制表示
sha1_hash = sha1.hexdigest()print("SHA-1 哈希值:", sha1_hash)
输出:
SHA-1 哈希值: 0a0a9f2a6772942557ab5355d76af442f8f65e01
文献参考:
https://www.cnblogs.com/scu-cjx/p/6878853.html
https://sunyunqiang.com/blog/sha1/
https://zh.wikipedia.org/zh-hans/SHA-1
相关文章:

CTF-Crypto学习记录-第四天 “ “ --- SHA1安全散列算法,实现原理。
文章目录 前言SHA-1加密算法介绍关于SHA-1和MD5 SHA-1 加密过程原文处理设置初始值和数据结构定义加密运算原理过程 在python中调用SHA-1 前言 MD5学习MD5加密算法 SHA-1加密算法介绍 SHA-1(Secure Hash Algorithm1,安全散列算法1)是一种密…...

海南海口大型钢结构件3D扫描全尺寸三维测量平面度平行度检测-CASAIM中科广电
高精度三维扫描技术已经在大型工件制造领域发挥着重要作用,特别是在质量检测环节,高效、高精度,可以轻松实现全尺寸三维测量。本期,CASAIM要分享的应用是在大型钢结构件的关键部位尺寸及形位公差检测。 钢结构件,是将…...

【PyQt学习篇 · ④】:QWidget - 尺寸操作
文章目录 QWidget简介QWidget大小位置操作案例一案例二 QWidget尺寸限定操作案例 内容边距案例 QWidget简介 在PyQt中,QWidget是一个基本的用户界面类,用于创建可见的窗口组件。QWidget可以包含多种类型的子组件,如QPushButton、QLabel、QLi…...
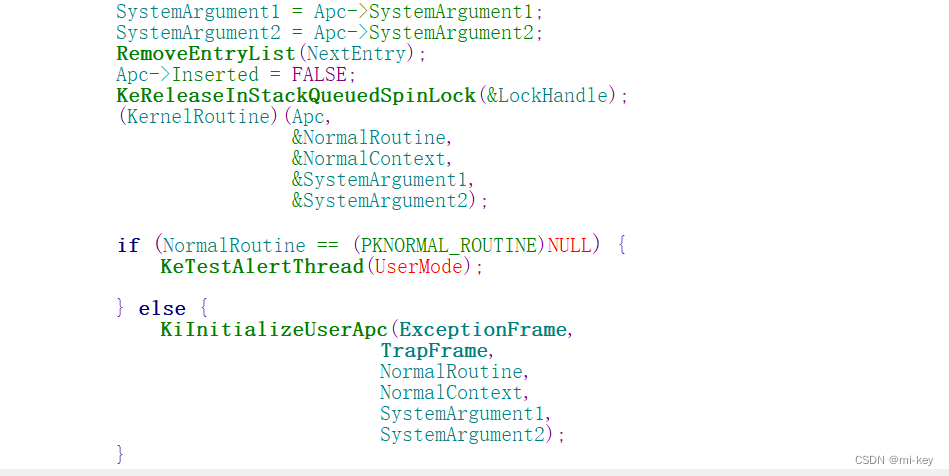
APC学习记录
文章目录 APC概念APC插入、执行过程逆向分析插入过程执行过程总结 代码演示参考资料 APC概念 APC全称叫做异步过程调用,英文名是 Asynchronous Procedure Call,在进行系统调用、线程切换、中断、异常时会进行触发执行的一段代码,其中主要分为…...
前端将图片储存table表格中,页面回显
<el-table :data"tableData" v-loading"loading" style"width: 100%" height"calc(100vh - 270px)" :size"tableSize"row-dblclick"enterClick"><el-table-column prop"name" label"文档…...

[论文阅读]Ghost-free High Dynamic Range Imaging with Context-aware Transformer
多帧高动态范围成像(High Dynamic Range Imaging, HDRI/HDR)旨在通过合并多幅不同曝光程度下的低动态范围图像,生成具有更宽动态范围和更逼真细节的图像。如果这些低动态范围图像完全对齐,则可以很好地融合为HDR图像,但…...
例子效果)
react高阶成分(HOC)例子效果
使用React函数式组件写了一个身份验证的一个功能,示例通过高阶组件实现的一个效果展示: import React, { useState, useEffect } from react;// 定义一个高阶组件,它接受一个组件作为输入,并返回一个新的包装组件 const withAuth…...
)
【24种设计模式】工厂模式(Factory Pattern)
工厂模式是一种创建型设计模式,它提供了一种创建对象的方式,而无需暴露对象创建的逻辑。在这篇博客中,我们将介绍工厂模式的概念、使用场景以及示例代码。 概念 工厂模式是一种创建型设计模式,它提供了一种创建对象的方式&#…...

树——对称二叉树
leetcode题目地址 树为空树,亦为对称二叉树树非空时,仅需判断其左右子树是否对称判断左右子树对称 (1) 左右子树是否为空,有一个为空 便不对称, 都为空或都不为空 可能对称 (2) 左右子树根节点值是否相同 (3) 判断 左子树 的 左子…...
拉扎维模拟CMOS集成电路设计西交张鸿老师课程P10~13视频学习记录
--------------------------------------------------------------------------------------------------------------------------------- p10 短沟道,除了沟长调,还可能出现速度饱和问题; 但是在拉扎维这本书里面没有考虑这个问题&#…...

3.线性神经网络
#pic_center R 1 R_1 R1 R 2 R^2 R2 目录 知识框架No.1 线性回归基础优化算法一、线性回归1、买房案例2、买房模型简化3、线性模型4、神经网络5、损失函数6、训练数据7、参数学习8、显示解9、总结 二、 基础优化算法1、梯度下降2、学习率3、小批量随机梯度下降4、批量大小5、…...

python常用内置函数的介绍和使用
Python具有丰富的内置函数,这些函数是Python语言提供的基础功能。以下是一些常用的内置函数的介绍和使用: print(): 打印输出指定的内容到屏幕。 print("Hello, World!") len(): 返回给定对象的长度或元素个数。 s "Hello, World!"…...

2023辽宁省赛E
Solution 题目大致分为三个步骤 计算 P ( S ) P(S) P(S)证明删除区间连续且找到最值位置根据最值位置求出答案 接下来过程中不合法的组合数都默认为 0 0 0 第 1 步 - 求出总值 考虑 S m { 1 , 2 , ⋯ , m } S_m \{1, 2, \cdots, m\} Sm{1,2,⋯,m} , 则有 $P(S_{n2}…...

visual studio 启用C++11
用C11取决于你所使用的编译器和开发环境。以下是一些常见的编译器和相应的启用C11的方法: GCC (GNU Compiler Collection): 对于 GCC,你可以在编译时使用 -stdc11 或更高的标志来启用C11支持。例如: g -stdc11 yourfile.cpp -o yourprogramCl…...
获取某个抖音用户的视频列表信息
思路 确定url确定并获取相关参数构造header发送请求解析数据输出数据 运行结果 代码 import requests # 获取某个用户的的视频信息,截至20231028,程序可以正常运行。 # 构造请求头header headers {User-Agent:..........................,Cookie:...…...
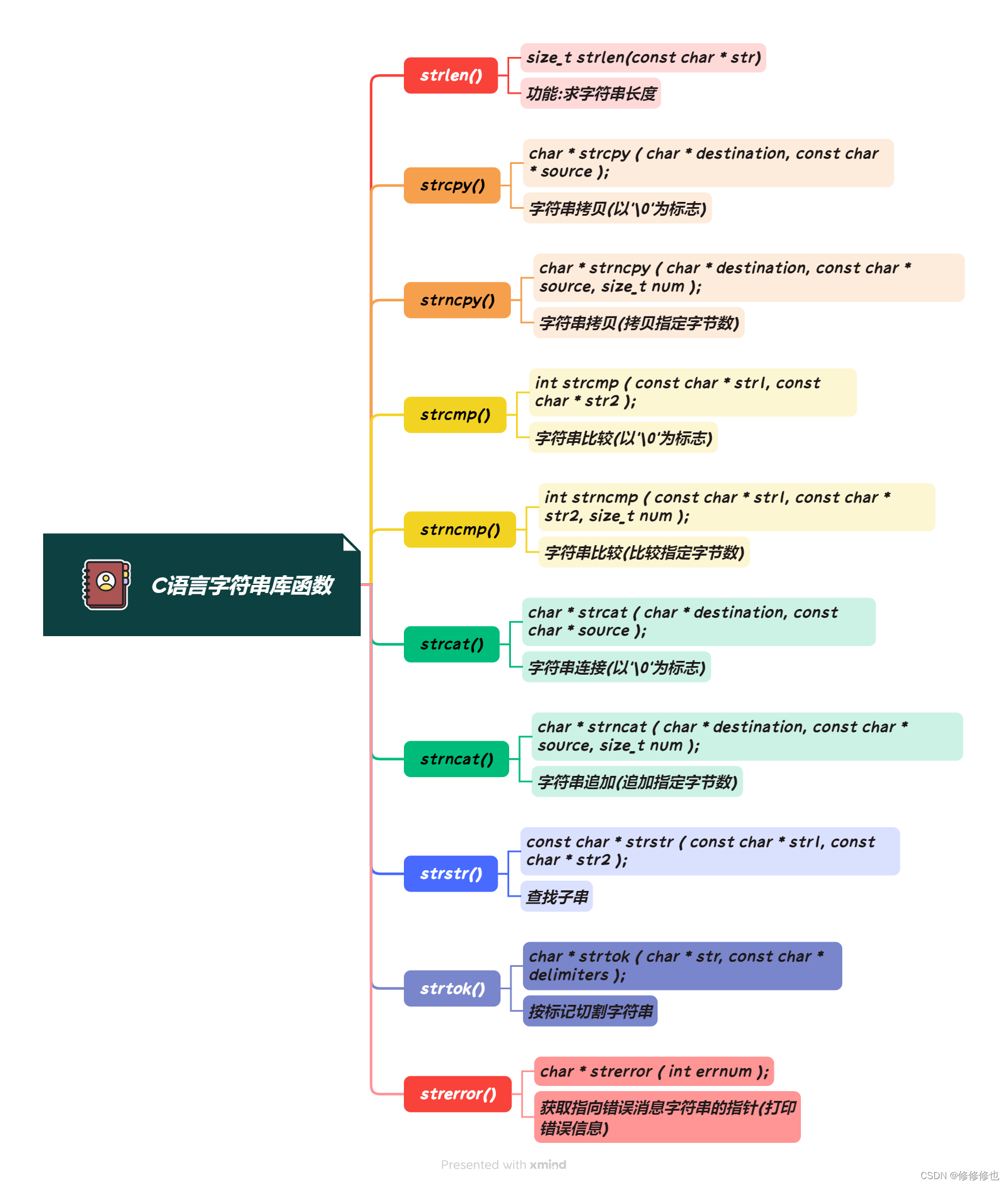
【C语言】strcpy()函数(字符串拷贝函数详解)
🦄个人主页:修修修也 🎏所属专栏:C语言 ⚙️操作环境:Visual Studio 2022 目录 一.strcpy()函数简介 1.函数功能 2.函数参数 1>.char * destination 2>.const char * source 3.函数返回值 4.函数头文件 二.strcpy()函数的具体使用 1.使用s…...

机器学习之IV编码,分箱WOE编码
IV的概念与作用 全称是Information Value,中文的意思是信息价值,或者信息量作用: 1、构建分类模型时,经常需要对特征进行筛选。 2、挑选特征的过程考虑的因素比较多,最主要和最直接的衡量标准是特征的预测能力&#…...

区块链技术与应用 【全国职业院校技能大赛国赛题目解析】第六套区块链系统部署与运维
第六套区块链系统部署与运维题目 环境 : ubuntu20 fisco : 2.8.0 子任务1-2-1: 搭建区块链系统并验证 题意: P2P起始端口 30500 channel起始端口 20500 JSONRPC 8945 使用Docker配置 使用 build_chain.sh 文件 进行生成节点文件 root@192-168-19-133:/yijiu/mode6# bas…...
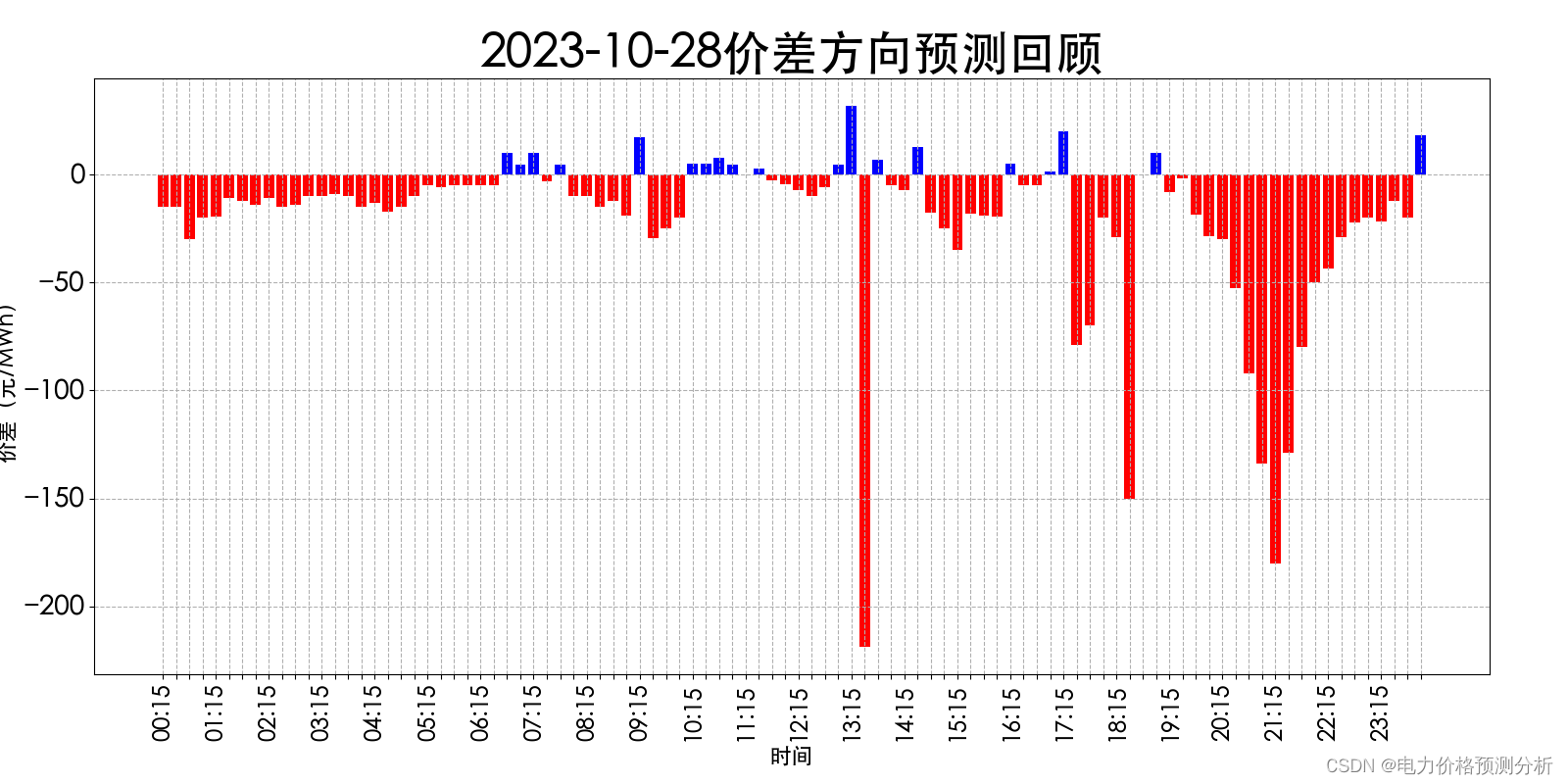
山西电力市场日前价格预测【2023-10-30】
日前价格预测 预测说明: 如上图所示,预测明日(2023-10-30)山西电力市场全天平均日前电价为309.35元/MWh。其中,最高日前电价为400.33元/MWh,预计出现在18:15。最低日前电价为0.00元/MWh,预计出…...
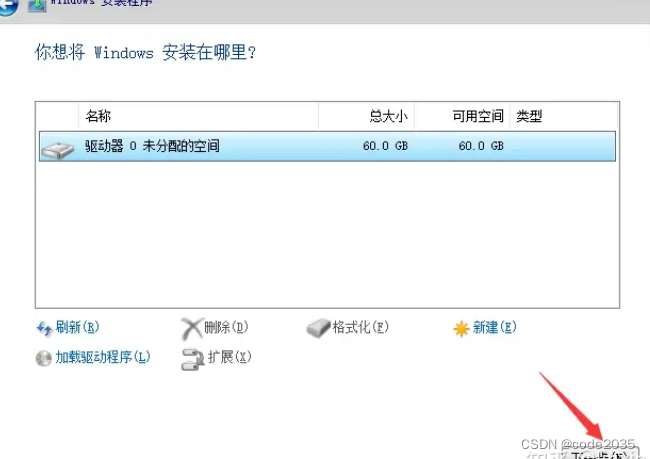
win10虚拟机安装教程
目录 1、安装VMware 10、12、16都可以,看个人选择 2、开始安装系统(以vm16为例) 3、在虚拟机中安装win10 完成 1、安装VMware 10、12、16都可以,看个人选择 下面链是我虚拟机安装包,需要可以下载。 YR云盘 软件安…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...
:LeetCode 142. 环形链表 II(Linked List Cycle II)详解)
Java详解LeetCode 热题 100(26):LeetCode 142. 环形链表 II(Linked List Cycle II)详解
文章目录 1. 题目描述1.1 链表节点定义 2. 理解题目2.1 问题可视化2.2 核心挑战 3. 解法一:HashSet 标记访问法3.1 算法思路3.2 Java代码实现3.3 详细执行过程演示3.4 执行结果示例3.5 复杂度分析3.6 优缺点分析 4. 解法二:Floyd 快慢指针法(…...

安全领域新突破:可视化让隐患无处遁形
在安全领域,隐患就像暗处的 “幽灵”,随时可能引发严重事故。传统安全排查手段,常常难以将它们一网打尽。你是否好奇,究竟是什么神奇力量,能让这些潜藏的隐患无所遁形?没错,就是可视化技术。它如…...
