文心一言 VS 讯飞星火 VS chatgpt (123)-- 算法导论10.4 4题
四、用go语言,对于一个含 n个结点的任意有根树,写出一个 O(n)时间的过程,输出其所有关键字该树以左孩子右兄弟表示法存储。
文心一言:
在计算机科学中,左孩子右兄弟表示法是一种用于表示树状结构的方法,其中每个节点都有两个指针:一个指向其第一个孩子(左孩子),另一个指向其下一个兄弟(右兄弟)。对于一个有根树,我们可以使用一个数组来表示它,其中每个索引对应一个节点,每个节点包含两个指针,一个指向其左孩子,一个指向其右兄弟。
下面是一个示例代码,演示了如何使用Go语言编写一个O(n)时间复杂度的过程,将一个含有n个节点的有根树以左孩子右兄弟表示法存储到数组中:
package main import "fmt" type TreeNode struct { Val int Left int Right int
} func storeTree(root int, node *TreeNode, nodes []int) { if nodes[root] != -1 { return } nodes[root] = root if node.Left != -1 { storeTree(node.Left, node, nodes) nodes[root] = nodes[node.Left] } if node.Right != -1 { storeTree(node.Right, node, nodes) nodes[root] = nodes[node.Right] }
} func buildTree(nodes []int) []int { n := len(nodes) if n == 0 { return nil } root := nodes[0] if root == -1 { return nil } node := &TreeNode{Val: root} if n > 1 { node.Left = buildTree(nodes[1:]) node.Right = buildTree(nodes[n-1:]) } return []int{node.Val, node.Left, node.Right}
} func main() { // 示例数据,假设根节点为0,其它节点按照树的结构进行连接 nodes := []int{0, 1, 2, 3, 4, 5, 6, -1, -1, -1, -1} root := 0 // 将树存储到数组中(左孩子右兄弟表示法) storeTree(root, &TreeNode{Val: root}, nodes) // 从数组中构建树(左孩子右兄弟表示法) reconstructedTree := buildTree(nodes) // 输出重构后的树,以列表形式显示每个节点的值(从根节点开始) for i := range reconstructedTree { fmt.Println(reconstructedTree[i]) }
}
这段代码定义了一个TreeNode结构体,包含节点的值和左右孩子的指针。storeTree函数用于将树以左孩子右兄弟表示法存储到数组中,buildTree函数用于从数组中构建树。最后,在main函数中,我们使用示例数据调用这两个函数来存储和重构树,并输出重构后的树的节点值。


讯飞星火:
package mainimport "fmt"type TreeNode struct {Val intLeft *TreeNodeRight *TreeNode
}func preorderTraversal(root *TreeNode) []int {if root == nil {return []int{}}stack := []*TreeNode{root}res := []int{}for len(stack) > 0 {node := stack[len(stack)-1]stack = stack[:len(stack)-1]if node.Right != nil {stack = append(stack, node.Right)}if node.Left != nil {stack = append(stack, node.Left)}res = append(res, node.Val)}return res
}func main() {root := &TreeNode{Val: 1}root.Left = &TreeNode{Val: 2}root.Right = &TreeNode{Val: 3}root.Left.Left = &TreeNode{Val: 4}root.Left.Right = &TreeNode{Val: 5}root.Right.Left = &TreeNode{Val: 6}root.Right.Right = &TreeNode{Val: 7}fmt.Println(preorderTraversal(root)) // 输出: [1 2 4 5 3 6 7]
}
360智脑:
以下是一个用Go语言实现的二叉树遍历函数,包括前序遍历、中序遍历和后序遍历:
package mainimport ("fmt"
)// 定义二叉树节点
type Node struct {key intleft; *Noderight; *Node
}// 中序遍历
func InOrder(root *Node) []int {res := make([]int, 0, len(root))inOrder(root.left, res)res = append(res, root.key)inOrder(root.right, res)return res
}// 前序遍历
func preOrder(root *Node) []int {if root == nil {return nil}res := []int{}res = append(res, root.key)preOrder(root.left)preOrder(root.right)return res
}// 后序遍历
func postOrder(root *Node) []int {if root == nil {return nil}res := []int{}postOrder(root.left)postOrder(root.right)res = append(res, root.key)return res
}// 递归遍历整个二叉树
func inOrder(root *Node, res []int) {for root != nil {res = append(res, root.key)inOrder(root.left, res)inOrder(root.right, res)}
}func main() {var root *Noderoot = &Node{key: 1, left: &Node{key: 2}, right: &Node{key: 3}}fmt.Println("In-order traversal:", inOrder(root)) // 输出:[1 2 3]
}
该程序使用递归算法实现二叉树的遍历,时间复杂度为 O(n),其中 n 是二叉树中的结点数。对于以左子树为根、右子树为左兄弟的表示法,该程序可以正确地输出所有关键字。
智谱清言:
以下是使用 Go 语言实现的一个 O(n) 时间过程,将含有 n 个节点的任意有根树转换为左孩子右兄弟表示法存储:
package main
import ( "fmt"
)
type TreeNode struct { Key int Left *TreeNode Right *TreeNode
}
func traversal(root *TreeNode) []int { if root == nil { return []int{} }left := traversal(root.Left) right := traversal(root.Right)left = append(left, root.Key) right = append(right, root.Key)return append(append(left, right...), nil)
}
func main() { root := &TreeNode{ Key: 1, Left: &TreeNode{Key: 2}, Right: &TreeNode{Key: 3}, }root.Left.Left = &TreeNode{Key: 4} root.Left.Right = &TreeNode{Key: 5} root.Right.Left = &TreeNode{Key: 6} root.Right.Right = &TreeNode{Key: 7}keys := traversal(root) fmt.Println(keys) // 输出:[1 2 4 5 3 6 7]
}
首先,我们定义了一个TreeNode结构体,用于表示树中的节点。然后,我们实现了一个traversal函数,该函数递归地遍历树,并将每个节点的键添加到结果切片中。最后,我们在main函数中创建了一个示例树,并调用traversal函数将其转换为左孩子右兄弟表示法。
这个过程的时间复杂度为 O(n),因为我们只需要遍历一次树即可。

通义千问:
这是一个涉及到数据结构和算法的问题,下面是一个可能的Go语言实现:
package mainimport "fmt"type Node struct {Val intLeft *NodeRight *Node
}func PrintValues(root *Node, arr []int) {if root != nil {arr = append(arr, root.Val)arr = PrintValues(root.Right, arr)arr = PrintValues(root.Left, arr)}return arr
}func main() {// 创建一个示例树root := &Node{Val: 1}root.Left = &Node{Val: 2}root.Right = &Node{Val: 3}root.Left.Left = &Node{Val: 4}root.Left.Right = &Node{Val: 5}// 打印树的关键字arr := PrintValues(root, []int{})fmt.Println(arr)
}
这个程序首先定义了一个Node结构体用于表示树的每一个节点,其中包含一个整型值Val以及指向其左右孩子的指针。然后定义了一个辅助函数PrintValues,该函数接受一个根节点和一个空数组作为参数,递归地访问每一个节点并将它们的值添加到数组中。最后,在主函数中创建了一个示例树,并调用PrintValues函数打印出树的所有关键字。
请注意,上述代码并未实现"左孩子右兄弟"表示法,因为原始问题并未提供足够的信息说明如何将给定的树转换为这种表示法。如果需要实现这一转换过程,可能需要用到更复杂的算法和技术。

天工:
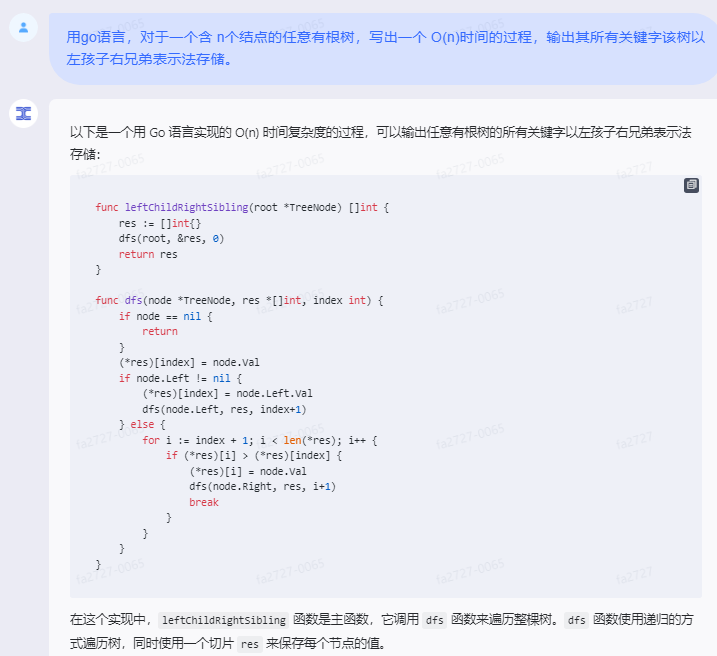
以下是一个用 Go 语言实现的 O(n) 时间复杂度的过程,可以输出任意有根树的所有关键字以左孩子右兄弟表示法存储:
func leftChildRightSibling(root *TreeNode) []int {res := []int{}dfs(root, &res, 0)return res
}func dfs(node *TreeNode, res *[]int, index int) {if node == nil {return}(*res)[index] = node.Valif node.Left != nil {(*res)[index] = node.Left.Valdfs(node.Left, res, index+1)} else {for i := index + 1; i < len(*res); i++ {if (*res)[i] > (*res)[index] {(*res)[i] = node.Valdfs(node.Right, res, i+1)break}}}
}
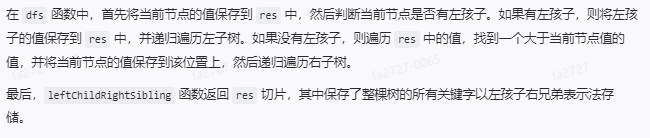
在这个实现中,leftChildRightSibling 函数是主函数,它调用 dfs 函数来遍历整棵树。dfs 函数使用递归的方式遍历树,同时使用一个切片 res 来保存每个节点的值。
在 dfs 函数中,首先将当前节点的值保存到 res 中,然后判断当前节点是否有左孩子。如果有左孩子,则将左孩子的值保存到 res 中,并递归遍历左子树。如果没有左孩子,则遍历 res 中的值,找到一个大于当前节点值的值,并将当前节点的值保存到该位置上,然后递归遍历右子树。
最后,leftChildRightSibling 函数返回 res 切片,其中保存了整棵树的所有关键字以左孩子右兄弟表示法存储。
灵小智:
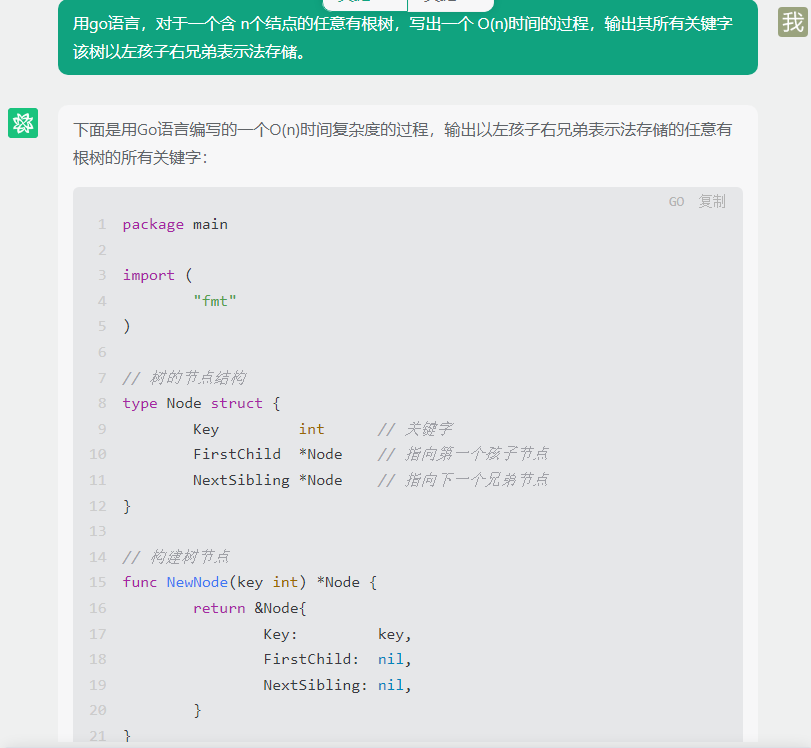
下面是用Go语言编写的一个O(n)时间复杂度的过程,输出以左孩子右兄弟表示法存储的任意有根树的所有关键字:
package mainimport ("fmt"
)// 树的节点结构
type Node struct {Key int // 关键字FirstChild *Node // 指向第一个孩子节点NextSibling *Node // 指向下一个兄弟节点
}// 构建树节点
func NewNode(key int) *Node {return &Node{Key: key,FirstChild: nil,NextSibling: nil,}
}// 将树转换为左孩子右兄弟表示法
func ConvertToLSRS(root *Node, lsrs []int) {if root == nil {return}// 处理当前节点lsrs[root.Key] = -1// 处理子节点child := root.FirstChildif child != nil {lsrs[root.Key] = child.KeyConvertToLSRS(child, lsrs)}// 处理兄弟节点sibling := root.NextSiblingif sibling != nil {lsrs[sibling.Key] = -1ConvertToLSRS(sibling, lsrs)}
}// 输出左孩子右兄弟表示法的关键字
func PrintLSRS(lsrs []int) {fmt.Println("左孩子右兄弟表示法存储的关键字:")for i, key := range lsrs {if key != -1 {fmt.Printf("节点 %d 的关键字为 %d\n", key, i)}}
}func main() {// 构建一个示例树root := NewNode(1)node2 := NewNode(2)node3 := NewNode(3)node4 := NewNode(4)root.FirstChild = node2node2.NextSibling = node3node3.NextSibling = node4// 初始化关键字数组n := 5 // 根据实际情况设置n的值,这里示例取5lsrs := make([]int, n)// 转换为左孩子右兄弟表示法ConvertToLSRS(root, lsrs)// 输出结果PrintLSRS(lsrs)
}
运行上述代码,将得到输出:
左孩子右兄弟表示法存储的关键字:
节点 2 的关键字为 1
节点 3 的关键字为 2
节点 4 的关键字为 3


chatgpt:
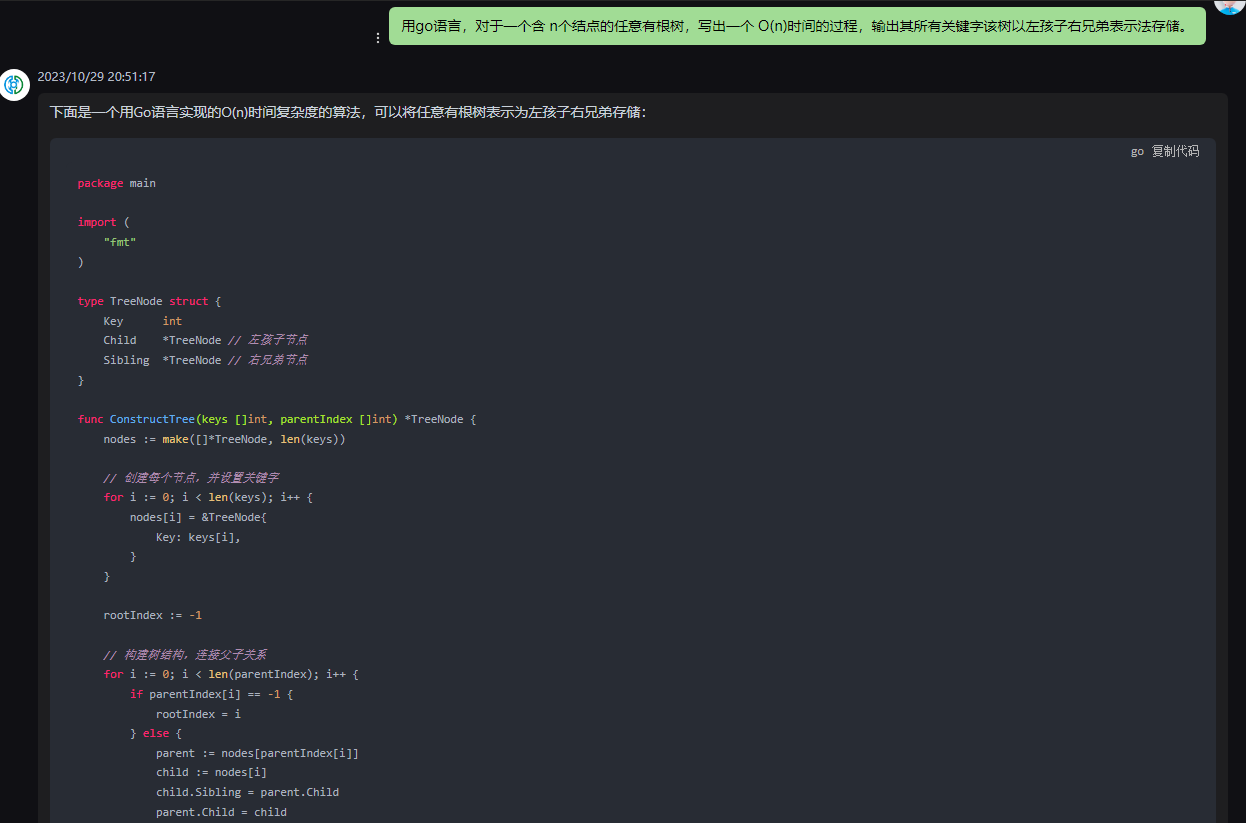
下面是一个用Go语言实现的O(n)时间复杂度的算法,可以将任意有根树表示为左孩子右兄弟存储:
package mainimport ("fmt"
)type TreeNode struct {Key intChild *TreeNode // 左孩子节点Sibling *TreeNode // 右兄弟节点
}func ConstructTree(keys []int, parentIndex []int) *TreeNode {nodes := make([]*TreeNode, len(keys))// 创建每个节点,并设置关键字for i := 0; i < len(keys); i++ {nodes[i] = &TreeNode{Key: keys[i],}}rootIndex := -1// 构建树结构,连接父子关系for i := 0; i < len(parentIndex); i++ {if parentIndex[i] == -1 {rootIndex = i} else {parent := nodes[parentIndex[i]]child := nodes[i]child.Sibling = parent.Childparent.Child = child}}return nodes[rootIndex]
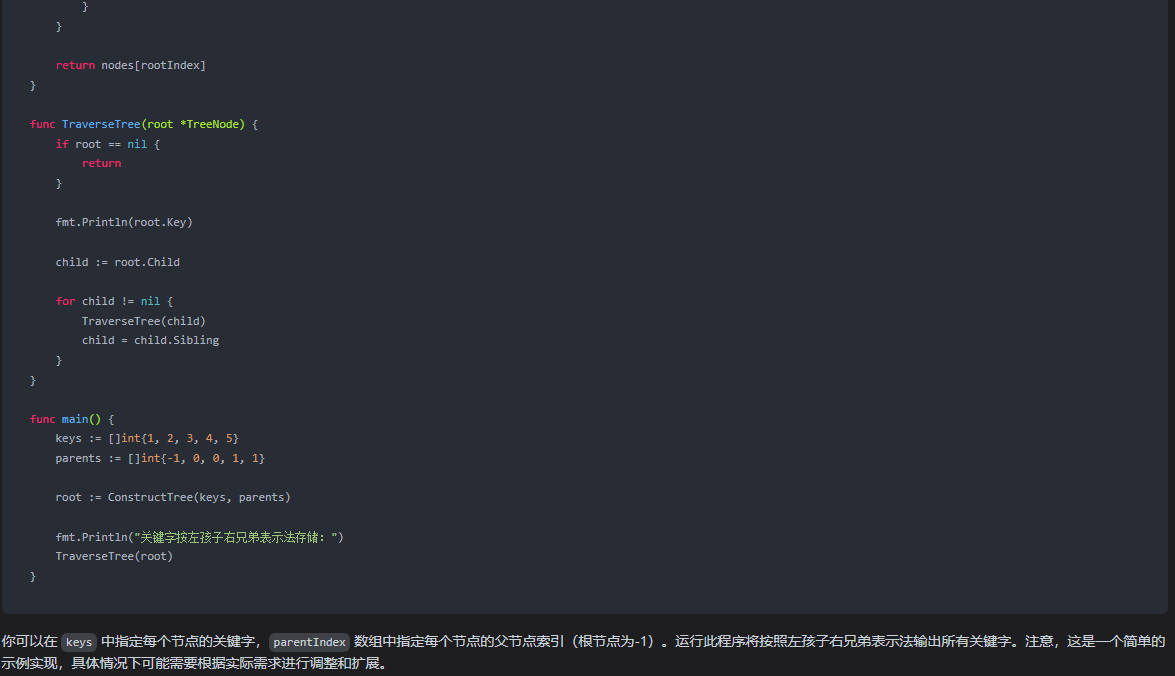
}func TraverseTree(root *TreeNode) {if root == nil {return}fmt.Println(root.Key)child := root.Childfor child != nil {TraverseTree(child)child = child.Sibling}
}func main() {keys := []int{1, 2, 3, 4, 5}parents := []int{-1, 0, 0, 1, 1}root := ConstructTree(keys, parents)fmt.Println("关键字按左孩子右兄弟表示法存储:")TraverseTree(root)
}
你可以在 keys 中指定每个节点的关键字,parentIndex 数组中指定每个节点的父节点索引(根节点为-1)。运行此程序将按照左孩子右兄弟表示法输出所有关键字。注意,这是一个简单的示例实现,具体情况下可能需要根据实际需求进行调整和扩展。
相关文章:

文心一言 VS 讯飞星火 VS chatgpt (123)-- 算法导论10.4 4题
四、用go语言,对于一个含 n个结点的任意有根树,写出一个 O(n)时间的过程,输出其所有关键字该树以左孩子右兄弟表示法存储。 文心一言: 在计算机科学中,左孩子右兄弟表示法是一种用于表示树状结构的方法,其…...
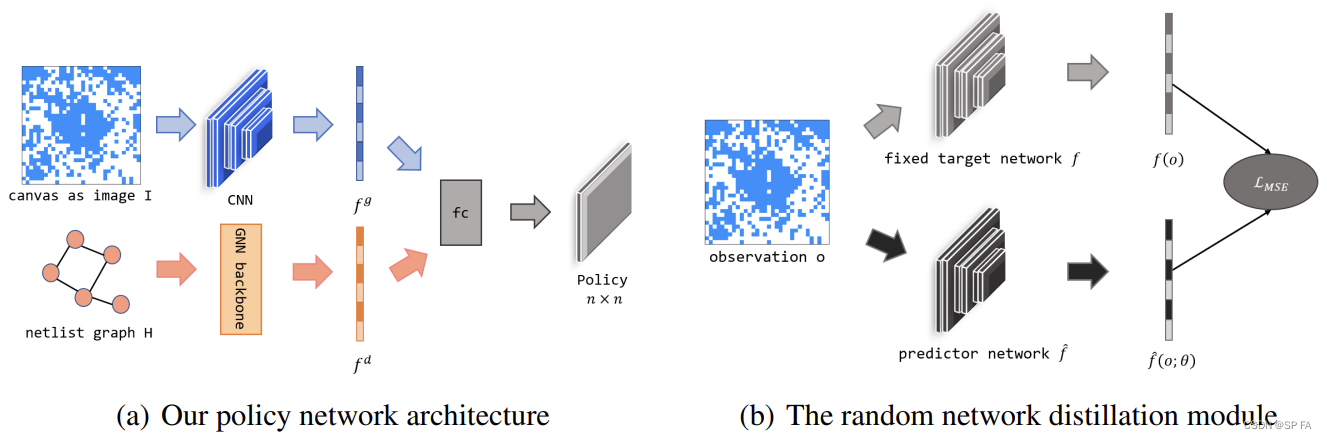
[读论文] On Joint Learning for Solving Placement and Routing in Chip Design
0. Abstract 由于 GPU 在加速计算方面的优势和对人类专家的依赖较少,机器学习已成为解决布局和布线问题的新兴工具,这是现代芯片设计流程中的两个关键步骤。它仍处于早期阶段,存在一些基本问题:可扩展性、奖励设计和端到端学习范…...

L2-1 插松枝
L2-1 插松枝 分数 25 全屏浏览题目 切换布局 作者 陈越 单位 浙江大学 人造松枝加工场的工人需要将各种尺寸的塑料松针插到松枝干上,做成大大小小的松枝。他们的工作流程(并不)是这样的: 每人手边有一只小盒子,初始…...

Android 使用ContentObserver监听SettingsProvider值的变化
1、Settings原理 Settings 设置、保存的一些值,最终是存储到 SettingsProvider 的数据库 例如: Settings.Global.putInt(getContentResolver(), "SwitchLaunch", 0); Settings.System.putInt(getContentResolver(), "SwitchLaunch&quo…...
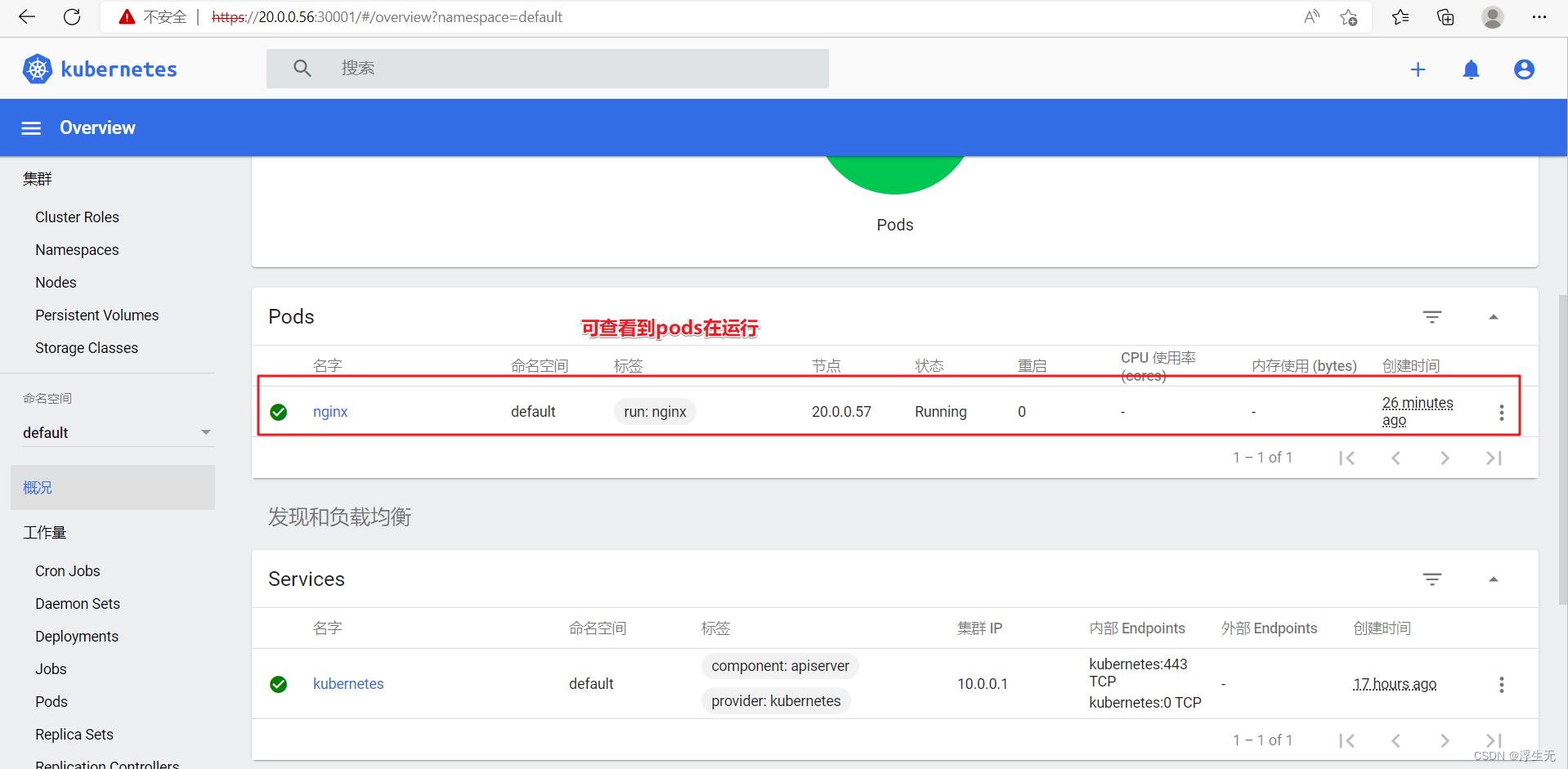
二进制安装部署k8s
概要 常见的K8S按照部署方式 minikube 是一个工具,可以在本地快速运行一个单节点微型K8S,仅用于学习,预习K8S的一些特性使用。 Kubeadmin kubeadmin也是一个工具,特工kubeadm init 和kubedm join,用于快速部署k8s…...
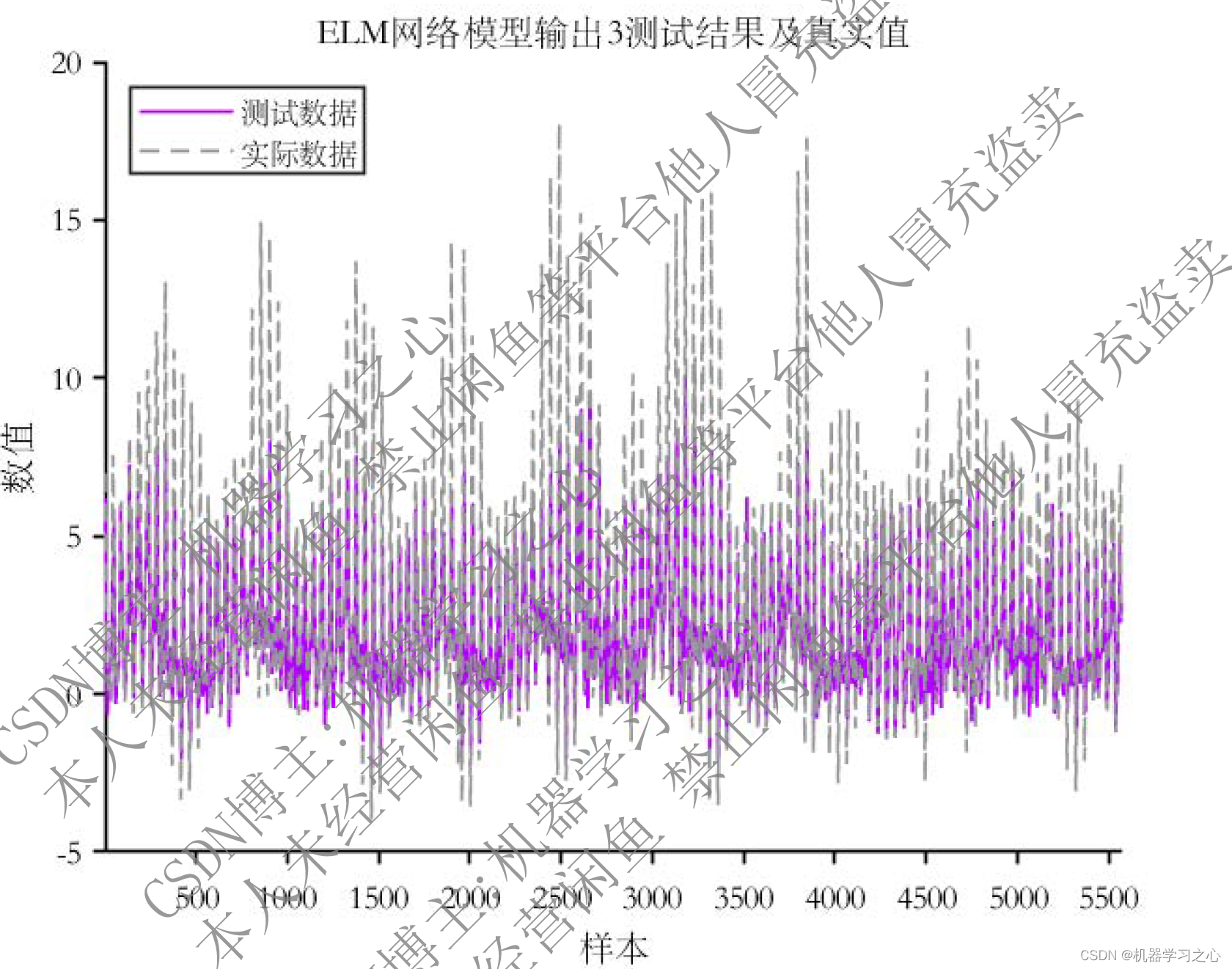
多输入多输出 | Matlab实现k-means-ELM(k均值聚类结合极限学习机)多输入多输出组合预测
多输入多输出 | Matlab实现k-means-ELM(k均值聚类结合极限学习机)多输入多输出组合预测 目录 多输入多输出 | Matlab实现k-means-ELM(k均值聚类结合极限学习机)多输入多输出组合预测预测效果基本描述程序设计参考资料 预测效果 基…...

ITSource 分享 第5期【校园信息墙系统】
项目介绍 本期给大家介绍一个 校园信息墙 系统,可以发布信息,表白墙,分享墙,校园二手买卖,咨询分享等墙信息。整个项目还是比较系统的,分为服务端,管理后台,用户Web端,小…...
记 : CTF2023羊城杯 - Reverse 方向 Blast 题目复现and学习记录
文章目录 前言题目分析and复习过程exp 前言 羊城杯题目复现: 第一题 知识点 :DES算法 : 链接:Ez加密器 第二题 知识点 :动态调试 : 链接:CSGO 这一题的查缺补漏: 虚假控制流的去除…...

【数据结构练习题】删除有序数组中的重复项
✨博客主页:小钱编程成长记 🎈博客专栏:数据结构练习题 🎈相关博文:消失的数字 — 三种解法超详解 删除有序数组中的重复项 1.🎈题目2. 🎈解题思路3. 🎈具体代码🎇总结 1…...
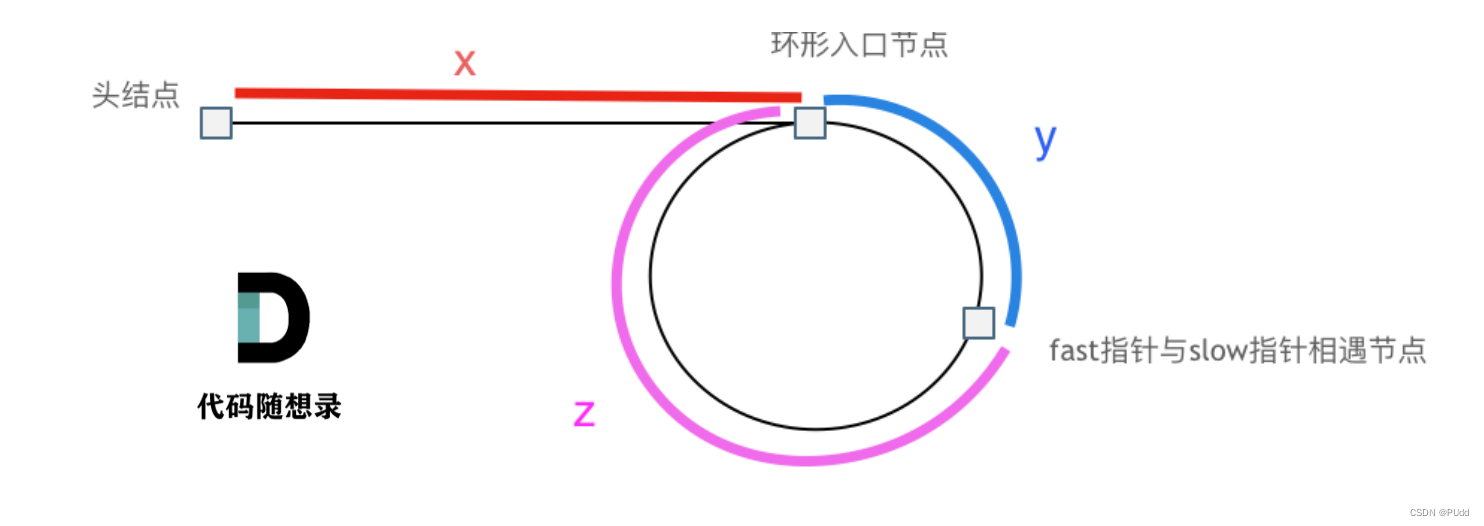
leetcode-链表
链表是一个用指针串联起来的线性结构,每个结点由数据域和指针域构成,指针域存放的是指向下一个节点的指针,最后一个节点指向NULL,第一个结点称为头节点head。 常见的链表有单链表、双向链表、循环链表。双向链表就是多了一个pre指…...
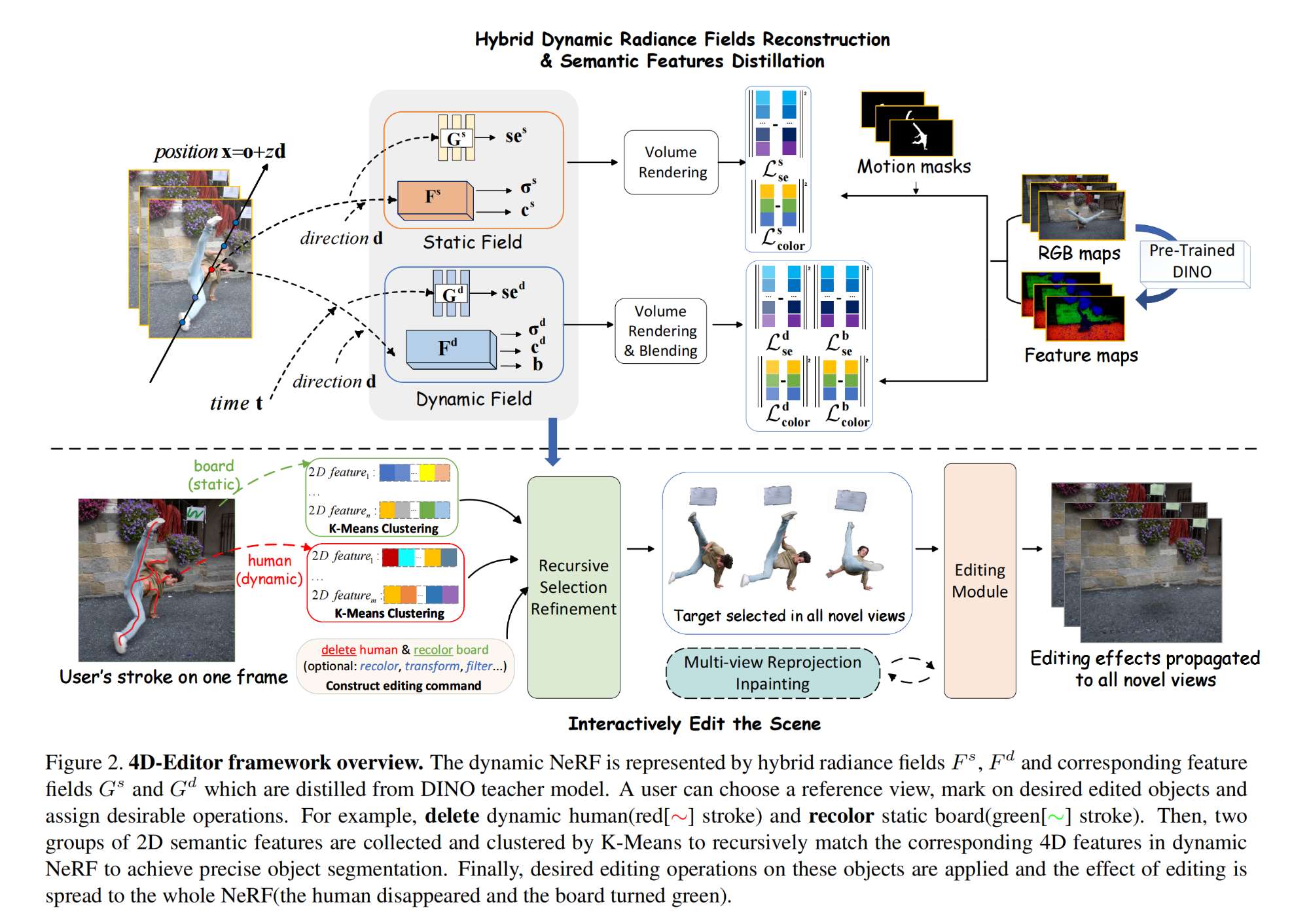
CV计算机视觉每日开源代码Paper with code速览-2023.10.27
精华置顶 墙裂推荐!小白如何1个月系统学习CV核心知识:链接 点击CV计算机视觉,关注更多CV干货 论文已打包,点击进入—>下载界面 点击加入—>CV计算机视觉交流群 1.【基础网络架构:Transformer】(Ne…...
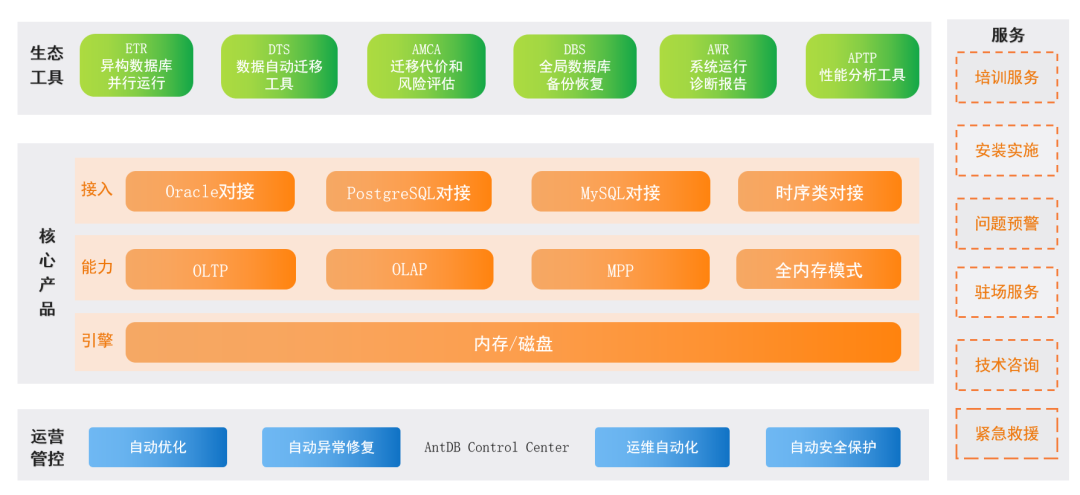
“赋能信创,物联未来” AntDB数据库携高可用解决方案亮相2023世界数字经济大会
10月14日,在2023世界数字经济大会暨京甬信创物联网产融对接会上,AntDB数据库技术总监北陌应邀发表《AntDB国产分布式数据库创新演进与高可用解决方案》主题演讲,就AntDB数据库助力客户数智化升级的高可用信创解决方案进行了详实、真挚地分享&…...
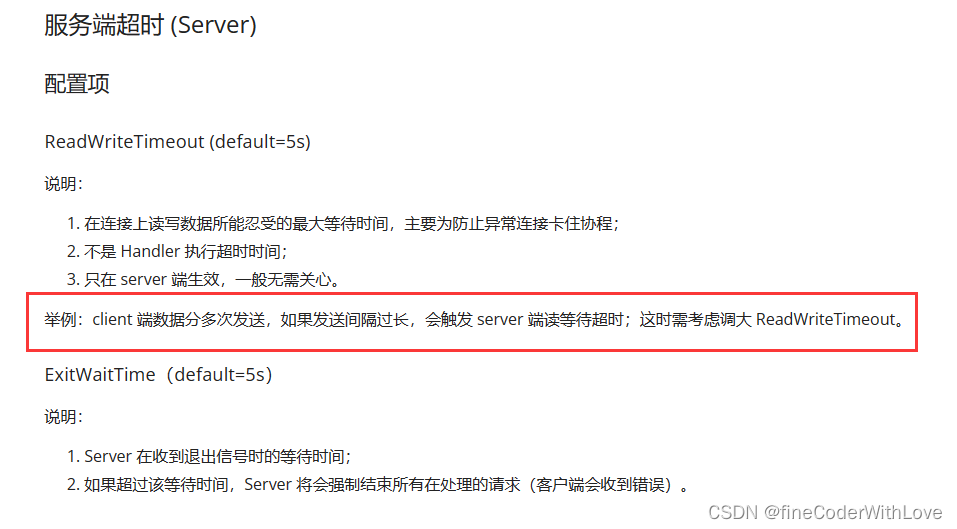
Kitex踩坑 [Error] KITEX: processing request error,i/o timeout
报错问题 2023/010/28 17:20:10.250768 default_server_handler.go:234: [Error] KITEX: processing request error, remoteService, remoteAddr127.0.0.1:65425, errordefault codec read failed: read tcp 127.0.0.1:8888->127.0.0.1:65425: i/o timeout 分析原因 Hert…...

前端移动web高级详细解析二
移动 Web 第二天 01-空间转换 空间转换简介 空间:是从坐标轴角度定义的 X 、Y 和 Z 三条坐标轴构成了一个立体空间,Z 轴位置与视线方向相同。 空间转换也叫 3D转换 属性:transform 平移 transform: translate3d(x, y, z); transform…...

Cesium 展示——对每段线、点、label做分组实体管理
文章目录 需求分析需求 对多组实体的管理,每组实体中包含多个点和一条线,并可对该组进行删除操作 分析 删除操作中用到了 viewer.entities.remove(radarEntity); 根据ID获取实体var radar = viewer.entities.getById(radar); viewer.entities.remove(radar );...

前端学习之Babel转码器
前言 Babel转码器可以将ES6转为ES5代码,从而在老版本的浏览器运行。这说明你可以用ES6的方式编码,又不用担心现有环境是否支持。 浏览器支持性查看:https://caniuse.com/ Babel官网:https://babeljs.io/ Babel安装流程 安装Babe…...

智能井盖监测系统功能,万宾科技传感器效果
智能井盖传感器的出现是高科技产品的更新换代,同时也是智慧城市建设中的需求。在智慧城市建设过程之中,高科技产品的应用数不胜数,智能井盖传感器的出现,解决了城市道路安全保护着城市地下生命线,改善着传统井盖带来的…...

LangChain+LLM实战---BERT主要的创新之处和注意力机制中的QKV
BERT主要的创新之处 BERT(Bidirectional Encoder Representations from Transformers)是一种基于Transformer架构的预训练语言模型,由Google在2018年提出。它的创新之处主要包括以下几个方面: 双向性(Bidirectional&…...
)
使用 @antfu/eslint-config 配置 eslint (包含兼容uniapp方法)
安装 pnpm i -D eslint antfu/eslint-config创建 eslint.config.js 文件 // 如果没有在 page.json 配置 "type": "module" const antfu require(antfu/eslint-config).default module.exports antfu()// 配置了 "type": "module" …...
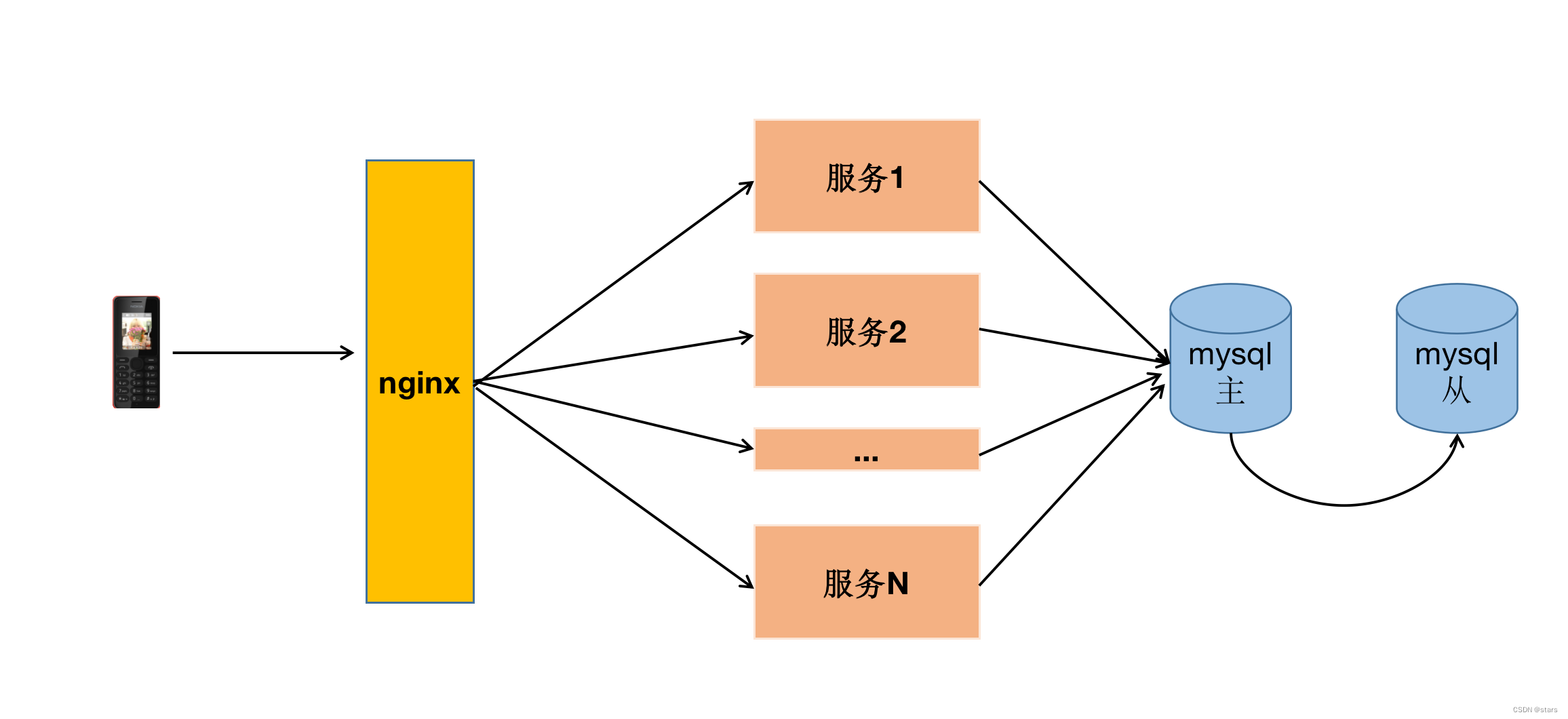
我的架构复盘
1、背景 我目前公司研发中心担任软件研发负责人,研发中心分为3组,总共有30多人。研发中心主要开发各类生产辅助工具,比如巡检、安全教育等系统。系统不对外,只在公司内部使用。 就我个人来说,作为研发负责人…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

LCTF液晶可调谐滤波器在多光谱相机捕捉无人机目标检测中的作用
中达瑞和自2005年成立以来,一直在光谱成像领域深度钻研和发展,始终致力于研发高性能、高可靠性的光谱成像相机,为科研院校提供更优的产品和服务。在《低空背景下无人机目标的光谱特征研究及目标检测应用》这篇论文中提到中达瑞和 LCTF 作为多…...

redis和redission的区别
Redis 和 Redisson 是两个密切相关但又本质不同的技术,它们扮演着完全不同的角色: Redis: 内存数据库/数据结构存储 本质: 它是一个开源的、高性能的、基于内存的 键值存储数据库。它也可以将数据持久化到磁盘。 核心功能: 提供丰…...

高防服务器价格高原因分析
高防服务器的价格较高,主要是由于其特殊的防御机制、硬件配置、运营维护等多方面的综合成本。以下从技术、资源和服务三个维度详细解析高防服务器昂贵的原因: 一、硬件与技术投入 大带宽需求 DDoS攻击通过占用大量带宽资源瘫痪目标服务器,因此…...
