【通信原理】第二章|确知信号
前言
那么这里博主先安利一些干货满满的专栏了!
首先是博主的高质量博客的汇总,这个专栏里面的博客,都是博主最最用心写的一部分,干货满满,希望对大家有帮助。
- 高质量博客汇总
文章目录
- 前言
- 第二章 确知信号
- 1. 确知信号的类型
- 2. 确知信号的频域性质
- 2.1 功率信号的频谱
- 2.2 周期性方波的频谱
- 2.3 能量信号的频谱密度
- 2.4 矩形脉冲的频谱密度
- 2.5 常用的傅里叶变换
- 2.6 能量信号的能量谱密度
- 2.7 功率信号的功率谱密度
- 3. 确知信号的时域性质
- 3.1 能量信号的自相关函数
- 3.2 功率信号的自相关函数
- 3.3 能量信号的互相关函数
- 3.4 功率信号的互相关函数
第二章 确知信号
1. 确知信号的类型
代表信号电压或者电流的时间波形 s ( t ) s(t) s(t)
s ( t ) s(t) \quad s(t)
信号的能量,单位焦耳。
E = ∫ − ∞ ∞ s 2 ( t ) d t E = \int_{-\infty }^{\infty} s^2(t)\mathrm{d}t E=∫−∞∞s2(t)dt
如果这个数是一个正的有限值,则信号为能量信号。与此同时,能量信号的平均功率 P = 0 P=0 P=0。
平均功率定义如下。
P = lim T → ∞ ∫ − T / 2 T / 2 s 2 ( t ) d t P = \lim_{T \to \infty } \int_{-T/2}^{T/2}s^2(t)\mathrm{d}t P=T→∞lim∫−T/2T/2s2(t)dt
两种信号。
- 能量信号,E为一个有限的正的值,但是平均功率P=0。
- 功率信号,其平均功率时等于一个有限的正值,但是能量为无穷大。
2. 确知信号的频域性质
2.1 功率信号的频谱
功率信号一般认为是周期的。(别管这么多,书上就是这样写的)
令一个周期信号 s ( t ) s(t) s(t)的周期为 T 0 T_0 T0,频谱函数可以定义成以下形式。
C n = C ( n f 0 ) = 1 T 0 ∫ − T 0 / 2 T 0 / 2 s ( t ) e − j 2 π n f 0 t d t f 0 = 1 / T 0 n 为整数 , − ∞ < n < ∞ C ( n f 0 ) 表示 C 是 n f 0 的函数,并简记为 C n C_n = C(nf_0) = \frac{1}{T_0}\int_{-T_0/2}^{T_0/2}s(t)e^{-j2\pi nf_0t}\mathrm{d}t \\ f_0 = 1/T_0 \\ n为整数, -\infty<n<\infty \\ C(nf_0)表示C是nf_0的函数,并简记为C_n Cn=C(nf0)=T01∫−T0/2T0/2s(t)e−j2πnf0tdtf0=1/T0n为整数,−∞<n<∞C(nf0)表示C是nf0的函数,并简记为Cn
傅立叶级数可以把 s ( t ) s(t) s(t)展开。
s ( t ) = ∑ n = − ∞ ∞ C n e j 2 π n t / T 0 s(t) = \sum_{n=-\infty}^{\infty} C_ne^{j2\pi nt/T_0} s(t)=n=−∞∑∞Cnej2πnt/T0
展开需要满足傅立叶级数的狄利克雷条件,一般信号是可以满足的。
当 n = 0 n=0 n=0的时候,是 s ( t ) s(t) s(t)的直流分量。
C 0 = 1 T 0 ∫ − T 0 / 2 T 0 / 2 s ( t ) d t C_{0}=\frac{1}{T_{0}} \int_{-T_{0} / 2}^{T_{0} / 2} s(t) \mathrm{d} t C0=T01∫−T0/2T0/2s(t)dt
频谱函数 C n C_n Cn是一个复数。
C n = ∣ C n ∣ e j θ n C_{n}=\left|C_{n}\right| \mathrm{e}^{\mathrm{j} \theta_{n}} Cn=∣Cn∣ejθn
对于周期性功率信号来说,频谱函数 C n C_n Cn是离散的。
重要性质。
C − n = 1 T 0 ∫ − T 0 / 2 T 0 / 2 s ( t ) e + j 2 π n f 0 t d t = [ 1 T 0 ∫ − T 0 / 2 T 0 / 2 s ( t ) e − j 2 π n f 0 t d t ] ∗ = C n ∗ C_{-n}=\frac{1}{T_{0}} \int_{-T_{0} / 2}^{T_{0} / 2} s(t) \mathrm{e}^{+\mathrm{j} 2 \pi n f_{0} t} \mathrm{~d} t=\left[\frac{1}{T_{0}} \int_{-T_{0} / 2}^{T_{0} / 2} s(t) \mathrm{e}^{-\mathrm{j} 2 \pi n f_{0} t} \mathrm{~d} t\right]^{*}=C_{n}^{*} C−n=T01∫−T0/2T0/2s(t)e+j2πnf0t dt=[T01∫−T0/2T0/2s(t)e−j2πnf0t dt]∗=Cn∗
傅立叶级数也可以展开成三角形式。
s ( t ) = C 0 + ∑ n = 1 ∞ [ a n cos ( 2 π n t / T 0 ) + b n sin ( 2 π n t / T 0 ) ] = C 0 + ∑ n = 1 ∞ [ a n 2 + b n 2 cos ( 2 π n t / T 0 + θ n ) ] 其中 θ n = − arctan ( b n / a n ) \begin{array}{l} \begin{aligned} s(t) & =C_{0}+\sum_{n=1}^{\infty}\left[a_{n} \cos \left(2 \pi n t / T_{0}\right)+b_{n} \sin \left(2 \pi n t / T_{0}\right)\right] \\ & =C_{0}+\sum_{n=1}^{\infty}\left[\sqrt{a_{n}^{2}+b_{n}^{2}} \cos \left(2 \pi n t / T_{0}+\theta_{n}\right)\right] \end{aligned}\\ 其中 \quad \theta_{n}=-\arctan \left(b_{n} / a_{n}\right) \end{array} s(t)=C0+n=1∑∞[ancos(2πnt/T0)+bnsin(2πnt/T0)]=C0+n=1∑∞[an2+bn2cos(2πnt/T0+θn)]其中θn=−arctan(bn/an)
2.2 周期性方波的频谱
C n = 1 T ∫ − τ / 2 τ / 2 V e − j 2 π n f 0 t d t = 1 T [ − V j 2 π n f 0 e − j 2 π n f 0 t ] − τ / 2 τ / 2 = V T e j 2 π n f 0 τ / 2 − e − j 2 π n f 0 τ / 2 j 2 π n f 0 = V π n f 0 T sin π n f 0 τ = V τ T S a ( n π τ T ) \begin{aligned} C_{n} & =\frac{1}{T} \int_{-\tau / 2}^{\tau / 2} V \mathrm{e}^{-\mathrm{j} 2 \pi n f_{0} t} \mathrm{~d} t=\frac{1}{T}\left[-\frac{V}{\mathrm{j} 2 \pi n f_{0}} \mathrm{e}^{-\mathrm{j} 2 \pi n f_{0} t}\right]_{-\tau / 2}^{\tau / 2} \\ & =\frac{V}{T} \frac{\mathrm{e}^{\mathrm{j} 2 \pi n f_{0} \tau / 2}-\mathrm{e}^{-\mathrm{j} 2 \pi n f_{0} \tau / 2}}{\mathrm{j} 2 \pi n f_{0}}=\frac{V}{\pi n f_{0} T} \sin \pi n f_{0} \tau= \frac{V \tau}{T} \mathrm{Sa}\left(\frac{n \pi \tau}{T}\right) \end{aligned} Cn=T1∫−τ/2τ/2Ve−j2πnf0t dt=T1[−j2πnf0Ve−j2πnf0t]−τ/2τ/2=TVj2πnf0ej2πnf0τ/2−e−j2πnf0τ/2=πnf0TVsinπnf0τ=TVτSa(Tnπτ)
记住答案,很重要。
C n = V τ T S a ( n π τ T ) C_n = \frac{V \tau}{T} \mathrm{Sa}\left(\frac{n \pi \tau}{T}\right) Cn=TVτSa(Tnπτ)
2.3 能量信号的频谱密度
注意叫法,功率信号的傅里叶系数 C n C_n Cn是叫做功率信号的频谱。
而,能量信号的傅里叶变换结果 S ( f ) S(f) S(f)叫做频谱密度。
S ( f ) = ∫ − ∞ ∞ s ( t ) e − j 2 π f t d t S(f)=\int_{-\infty}^{\infty} s(t) \mathrm{e}^{-\mathrm{j} 2 \pi f t} \mathrm{~d} t S(f)=∫−∞∞s(t)e−j2πft dt
S ( f ) S(f) S(f)的逆傅立叶变换就是原信号。
s ( t ) = ∫ − ∞ ∞ S ( f ) e j 2 π f t d f s(t)=\int_{-\infty}^{\infty} S(f) \mathrm{e}^{\mathrm{j} 2 \pi f t} \mathrm{~d} f s(t)=∫−∞∞S(f)ej2πft df
实能量信号的频谱密度和实功率信号的频谱有一个共同的特征,即负频谱和正频谱的模偶对称,相位奇对称。
∫ − ∞ ∞ s ( t ) e − j 2 π f t d t = [ ∫ − ∞ ∞ s ( t ) e + j 2 π f t d t ] ∗ S ( f ) = [ S ( − f ) ] ∗ \int_{-\infty}^{\infty} s(t) \mathrm{e}^{-\mathrm{j} 2 \pi f t} \mathrm{~d} t=\left[\int_{-\infty}^{\infty} s(t) \mathrm{e}^{+\mathrm{j} 2 \pi f t} \mathrm{~d} t\right]^{*} \\ S(f)=[S(-f)]^{*} ∫−∞∞s(t)e−j2πft dt=[∫−∞∞s(t)e+j2πft dt]∗S(f)=[S(−f)]∗
2.4 矩形脉冲的频谱密度
矩形脉冲的表达式为。
g τ ( t ) = { 1 ∣ t ∣ ⩽ τ / 2 0 ∣ t ∣ > τ / 2 g_{\tau}(t)=\left\{\begin{array}{ll} 1 & |t| \leqslant \tau / 2 \\ 0 & |t|>\tau / 2 \end{array}\right. gτ(t)={10∣t∣⩽τ/2∣t∣>τ/2
傅立叶变换结果为。
G τ ( f ) = τ S a ( π f τ ) G_\tau(f) = \tau \mathrm{Sa}(\pi f \tau) Gτ(f)=τSa(πfτ)
很重要,要记住。
2.5 常用的傅里叶变换
f ( t ) F ( w ) f ( t ) F ( w ) δ ( t ) 1 r e c t ( t / τ ) τ S a ( w τ / 2 ) 1 2 π δ ( w ) W 2 π S a ( W t 2 ) r e c t ( w W ) e j w 0 t 2 π δ ( w − w 0 ) c o s ( w 0 t ) π [ δ ( w − w 0 ) + δ ( w + w 0 ) ] s g n ( t ) 2 j w s i n ( w 0 t ) π j [ δ ( w − w 0 ) − δ ( w + w 0 ) ] j 1 π t s g n ( w ) e − α ∣ t ∣ 2 α α 2 + w 2 u ( t ) π δ ( w ) + 1 j w u ( t ) e − α t 1 α + j ω δ T ( t ) = ∑ n = − ∞ ∞ δ ( t − n T ) 2 π T ∑ n = − ∞ ∞ δ ( ω − n ⋅ 2 π T ) u ( t ) t e − α t 1 ( α + j ω ) 2 \begin{array}{cc|cc} \hline f(t) & F(w) & f(t) & F(w) \\ \hline \delta(t) & 1 & rect(t/\tau) & \tau Sa(w\tau/2) \\ 1 & 2\pi\delta(w) & \frac{W}{2\pi}Sa(\frac{Wt}{2}) & rect(\frac{w}{W}) \\ e^{jw_0t} & 2\pi\delta (w-w_0) & cos(w_0t) & \pi[\delta(w-w_0)+\delta(w+w_0)] \\ sgn(t) & \frac{2}{jw} & sin(w_0t) & \frac{\pi}{j}[\delta(w-w_0)-\delta(w+w_0)] \\ j\frac{1}{\pi t} & sgn(w) & e^{-\alpha |t| } & \frac{2\alpha}{\alpha ^2+w^2} \\ u(t) & \pi\delta(w)+\frac{1}{jw} & u(t) \mathrm{e}^{-\alpha t} & \frac{1}{\alpha+\mathrm{j} \omega}\\ \delta_{T}(t)=\sum_{n=-\infty}^{\infty} \delta(t-n T) & \frac{2 \pi}{T} \sum_{n=-\infty}^{\infty} \delta\left(\omega-n \cdot \frac{2 \pi}{T}\right) & u(t) t \mathrm{e}^{-\alpha t} & \frac{1}{(\alpha+\mathrm{j} \omega)^{2}} \\ \hline \end{array} f(t)δ(t)1ejw0tsgn(t)jπt1u(t)δT(t)=∑n=−∞∞δ(t−nT)F(w)12πδ(w)2πδ(w−w0)jw2sgn(w)πδ(w)+jw1T2π∑n=−∞∞δ(ω−n⋅T2π)f(t)rect(t/τ)2πWSa(2Wt)cos(w0t)sin(w0t)e−α∣t∣u(t)e−αtu(t)te−αtF(w)τSa(wτ/2)rect(Ww)π[δ(w−w0)+δ(w+w0)]jπ[δ(w−w0)−δ(w+w0)]α2+w22αα+jω1(α+jω)21
2.6 能量信号的能量谱密度
能量E。
E = ∫ − ∞ ∞ s 2 ( t ) d t E=\int_{-\infty}^{\infty} s^{2}(t) \mathrm{d} t E=∫−∞∞s2(t)dt
巴塞伐尔定理。
E = ∫ − ∞ ∞ s 2 ( t ) d t = ∫ − ∞ ∞ ∣ S ( f ) ∣ 2 d f E=\int_{-\infty}^{\infty} s^{2}(t) \mathrm{d} t=\int_{-\infty}^{\infty}|S(f)|^{2} \mathrm{~d} f E=∫−∞∞s2(t)dt=∫−∞∞∣S(f)∣2 df
能量谱密度。
G ( f ) = ∣ S ( f ) ∣ 2 ( J / H z ) G(f)=|S(f)|^{2} \quad(\mathrm{~J}/\mathrm{Hz}) G(f)=∣S(f)∣2( J/Hz)
由于信号 s ( t ) s(t) s(t)是实函数,所以 ∣ S ( f ) ∣ |S(f)| ∣S(f)∣是一个偶函数。
2.7 功率信号的功率谱密度
巴塞伐尔定理。
E = ∫ − T / 2 T / 2 s T 2 ( t ) d t = ∫ − ∞ ∞ ∣ S T ( f ) ∣ 2 d f E=\int_{-T / 2}^{T / 2} s_{T}^{2}(t) \mathrm{d} t=\int_{-\infty}^{\infty}\left|S_{T}(f)\right|^{2} \mathrm{~d} f E=∫−T/2T/2sT2(t)dt=∫−∞∞∣ST(f)∣2 df
功率谱密度。
P ( f ) = lim T → ∞ 1 T ∣ S T ( f ) ∣ 2 P(f) = \lim _{T \rightarrow \infty} \frac{1}{T}|S_{T}(f)|^{2} P(f)=T→∞limT1∣ST(f)∣2
功率用功率谱密度表示。
P = lim T → ∞ 1 T ∫ − ∞ ∞ ∣ S T ( f ) ∣ 2 d f = ∫ − ∞ ∞ P ( f ) d f P=\lim _{T \rightarrow \infty} \frac{1}{T} \int_{-\infty}^{\infty}\left|S_{T}(f)\right|^{2} \mathrm{~d} f=\int_{-\infty}^{\infty} P(f) \mathrm{d} f P=T→∞limT1∫−∞∞∣ST(f)∣2 df=∫−∞∞P(f)df
3. 确知信号的时域性质
确知信号再时域中的性质主要有自相关函数和互相关函数。
3.1 能量信号的自相关函数
R ( τ ) = ∫ − ∞ ∞ s ( t ) s ( t + τ ) d t − ∞ < τ < ∞ R(\tau)=\int_{-\infty}^{\infty} s(t) s(t+\tau) \mathrm{d} t \quad-\infty<\tau<\infty R(τ)=∫−∞∞s(t)s(t+τ)dt−∞<τ<∞
自相关函数反映了一个信号延迟 τ \tau τ后的同一信号间的相关程度。自相关函数 R ( τ ) R(\tau) R(τ)和时间t无关,只和时间差 τ \tau τ有关。
当 τ = 0 \tau=0 τ=0的时候,能量信号的自相关函数 R ( 0 ) R(0) R(0)等于信号的能量。
R ( 0 ) = E 前提是能量信号 R(0) = E \quad 前提是能量信号 R(0)=E前提是能量信号
此外, R ( τ ) R(\tau) R(τ)是偶函数。
自相关函数和能量谱密度的关系。
能量谱密度的逆傅立叶变换就是能量信号的自相关函数。
R ( τ ) = ∫ − ∞ ∞ ∣ S ( f ) ∣ 2 e j 2 π f τ d f R(\tau)=\int_{-\infty}^{\infty}|S(f)|^{2} \mathrm{e}^{\mathrm{j} 2 \pi f \tau} \mathrm{d} f R(τ)=∫−∞∞∣S(f)∣2ej2πfτdf
R ( τ ) R(\tau) R(τ)和 ∣ S ( f ) ∣ 2 |S(f)|^2 ∣S(f)∣2构成一对傅立叶变换。
3.2 功率信号的自相关函数
功率信号自相关函数的定义。
R ( τ ) = lim T → ∞ 1 T ∫ − T / 2 T / 2 s ( t ) s ( t + τ ) d t − ∞ < τ < ∞ R(\tau)=\lim _{T \rightarrow \infty} \frac{1}{T} \int_{-T / 2}^{T / 2} s(t) s(t+\tau) \mathrm{d} t \quad-\infty<\tau<\infty R(τ)=T→∞limT1∫−T/2T/2s(t)s(t+τ)dt−∞<τ<∞
由定义可以看出, τ = 0 \tau=0 τ=0的时候,功率信号的自相关函数 R ( 0 ) R(0) R(0)等于信号的平均功率。
R ( 0 ) = lim T → ∞ 1 T ∫ − T / 2 T / 2 s 2 ( t ) d t = P R(0)=\lim _{T \rightarrow \infty} \frac{1}{T} \int_{-T / 2}^{T / 2} s^{2}(t) \mathrm{d} t=P R(0)=T→∞limT1∫−T/2T/2s2(t)dt=P
功率信号的自相关函数也是偶函数。
对于周期性的功率信号,自相关函数的定义可以改写为。
R ( τ ) = 1 T 0 ∫ − T 0 / 2 T 0 / 2 s ( t ) s ( t + τ ) d t − ∞ < τ < ∞ R(\tau)=\frac{1}{T_{0}} \int_{-T_{0} / 2}^{T_{0} / 2} s(t) s(t+\tau) \mathrm{d} t \quad-\infty<\tau<\infty R(τ)=T01∫−T0/2T0/2s(t)s(t+τ)dt−∞<τ<∞
功率信号的自相关函数的傅立叶变换就是功率谱密度。
P ( f ) = ∫ − ∞ ∞ R ( τ ) e − j 2 π f τ d τ P(f)=\int_{-\infty}^{\infty} R(\tau) \mathrm{e}^{-\mathrm{j} 2 \pi f \tau} \mathrm{d} \tau P(f)=∫−∞∞R(τ)e−j2πfτdτ
3.3 能量信号的互相关函数
两个能量信号 s 1 ( t ) s_1(t) s1(t)和 s 2 ( t ) s_2(t) s2(t)的互相关函数定义如下。
R 12 ( τ ) = ∫ − ∞ ∞ s 1 ( t ) s 2 ( t + τ ) d t − ∞ < τ < ∞ R_{12}(\tau)=\int_{-\infty}^{\infty} s_{1}(t) s_{2}(t+\tau) \mathrm{d} t \quad-\infty<\tau<\infty R12(τ)=∫−∞∞s1(t)s2(t+τ)dt−∞<τ<∞
顺序很重要。
R 21 ( τ ) = R 12 ( − τ ) R_{21}(\tau) = R_{12}(-\tau) R21(τ)=R12(−τ)
互相关函数和能量谱密度的关系。
互能量谱密度定义。
S 12 ( f ) = S 1 ∗ ( f ) S 2 ( f ) S_{12}(f)=S_{1}^{*}(f) S_{2}(f) S12(f)=S1∗(f)S2(f)
所以互相关函数和互能量谱密度也是一对傅立叶变换。
S 12 ( f ) = ∫ − ∞ ∞ R 12 ( τ ) e − j 2 π / τ d τ S_{12}(f)=\int_{-\infty}^{\infty} R_{12}(\tau) \mathrm{e}^{-\mathrm{j} 2 \pi / \tau} \mathrm{d} \tau S12(f)=∫−∞∞R12(τ)e−j2π/τdτ
3.4 功率信号的互相关函数
两个功率信号的互相关函数定义为。
R 12 ( τ ) = lim T → ∞ 1 T ∫ − T / 2 T / 2 s 1 ( t ) s 2 ( t + τ ) d t R_{12}(\tau)=\lim _{T \rightarrow \infty} \frac{1}{T} \int_{-T / 2}^{T / 2} s_{1}(t) s_{2}(t+\tau) \mathrm{d} t R12(τ)=T→∞limT1∫−T/2T/2s1(t)s2(t+τ)dt
如果两个功率信号的周期相同,则其互相关函数的定义可以写成。
R 12 ( τ ) = 1 T ∫ − T / 2 T / 2 s 1 ( t ) s 2 ( t + τ ) d t − ∞ < τ < ∞ R_{12}(\tau)=\frac{1}{T} \int_{-T / 2}^{T / 2} s_{1}(t) s_{2}(t+\tau) \mathrm{d} t \quad-\infty<\tau<\infty R12(τ)=T1∫−T/2T/2s1(t)s2(t+τ)dt−∞<τ<∞
互功率谱定义。
C 12 = ( C n ) 1 ∗ ( C n ) 2 C_{12}=\left(C_{n}\right)_{1}^{*}\left(C_{n}\right)_{2} C12=(Cn)1∗(Cn)2
周期性功率信号的互功率谱 C 12 C_{12} C12是其互相关函数 R 12 ( τ ) R_{12}(\tau) R12(τ)的傅立叶级数的系数。
相关文章:

【通信原理】第二章|确知信号
前言 那么这里博主先安利一些干货满满的专栏了! 首先是博主的高质量博客的汇总,这个专栏里面的博客,都是博主最最用心写的一部分,干货满满,希望对大家有帮助。 高质量博客汇总 文章目录 前言 第二章 确知信号1. 确知…...
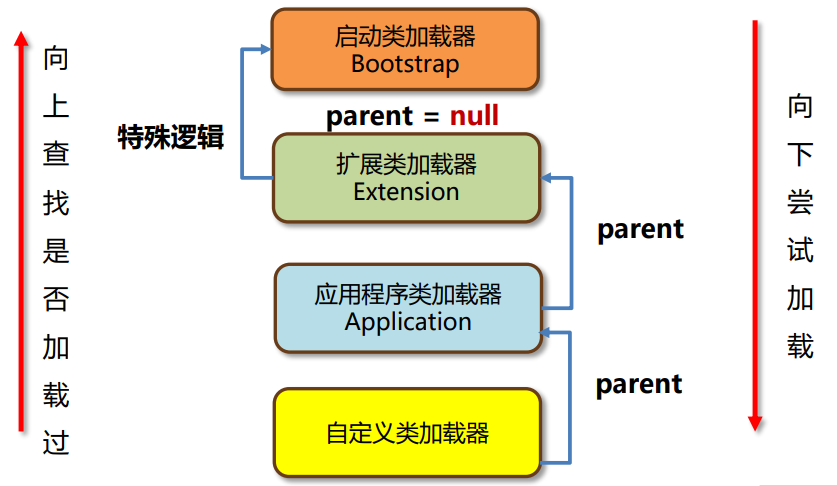
【JVM】类加载器
【JVM】类加载器 文章目录 【JVM】类加载器0. 类加载器概述1. 类加载器的分类1.1 启动类加载器1.2 Java中的默认类加载器1.2.1 扩展类加载器1.2.2 应用程序类加载器 2. 双亲委派机制2.1 类的双亲委派机制是什么?2.2 打破双亲委派机制2.2.1 自定义类加载器2.2.2 线程…...
利用Excel支持JUnit参数化测试
在JUnit里面,可以使用CsvFileSource读取csv文件进行参数化测试,可是CSV文件不支持格式,编辑颇为麻烦,尤其是多次编辑,因此自然想到是否可以使用Excel文件,可以有各种格式,支持各类数据。 最新开…...
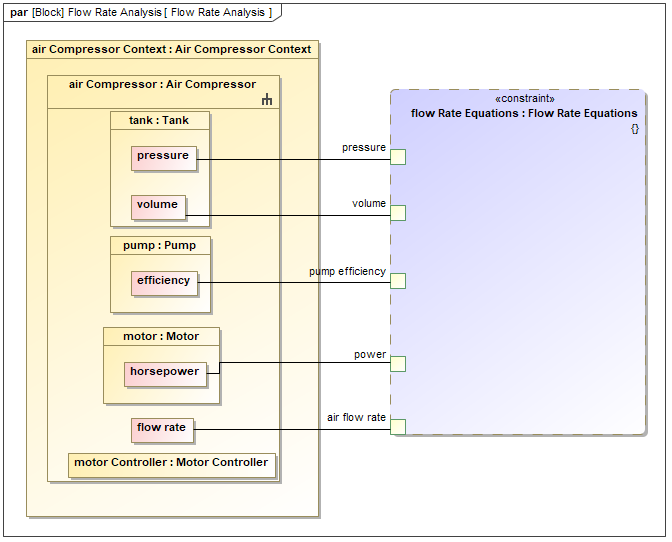
第三章 SysML入门|系统建模语言SysML实用指南学习
仅供个人学习记录 UML与SysML的联系 可以稍微参考UML与SysML的联系 UML(统一建模语言)和SysML(系统建模语言)是两种与建模相关的语言,它们之间存在联系和区别。 SysML的图分类如下图所示。 SysML 图概述 这里只…...

敏捷开发框架Scrum-概述
如果你是一个程序员,可能会觉得这是个程序开发框架。Scrum是一个敏捷开发框架。我们可以把Scrum理解成一个团队一次完成一小部分工作的方式。这种方式通过不断的实验和反馈循环来学习和改进。Scrum可以帮助团队以协作的方式逐步交付价值。 Scrum框架由一个Scrum团队…...

Hafnium启动过程分析
安全之安全(security)博客目录导读 目录 一、在安全世界中加载Hafnium和安全分区 二、通过TF-A启动 1、SP manifests 2、安全分区包 3、描述安全分区...
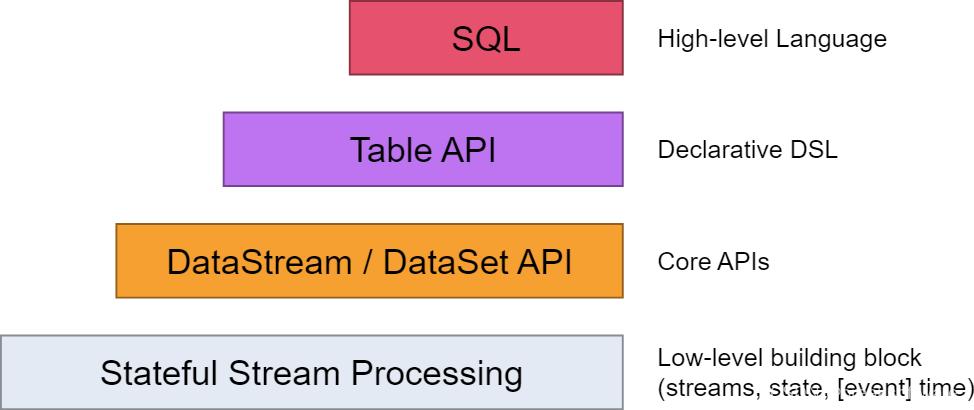
0基础学习PyFlink——使用Table API实现SQL功能
大纲 Souceschemadescriptor Sinkschemadescriptor Execute完整代码参考资料 《0基础学习PyFlink——使用PyFlink的Sink将结果输出到Mysql》一文中,我们讲到如何通过定义Souce、Sink和Execute三个SQL,来实现数据读取、清洗、计算和入库。 如下图所示SQL是最高层级的…...
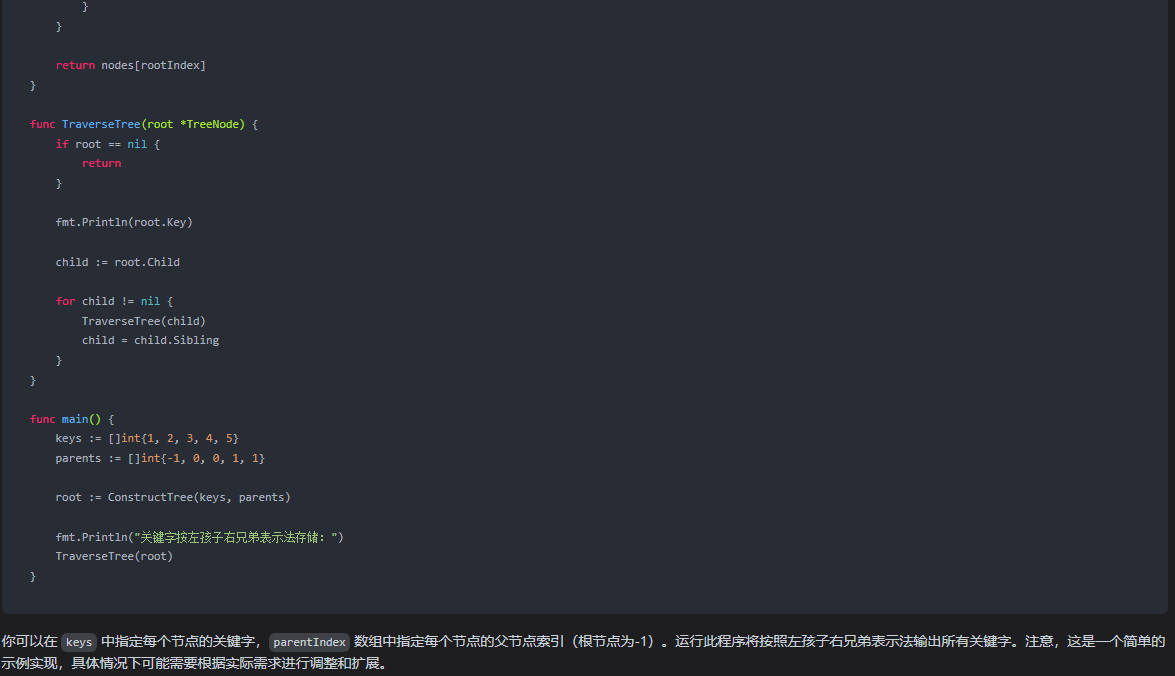
文心一言 VS 讯飞星火 VS chatgpt (123)-- 算法导论10.4 4题
四、用go语言,对于一个含 n个结点的任意有根树,写出一个 O(n)时间的过程,输出其所有关键字该树以左孩子右兄弟表示法存储。 文心一言: 在计算机科学中,左孩子右兄弟表示法是一种用于表示树状结构的方法,其…...
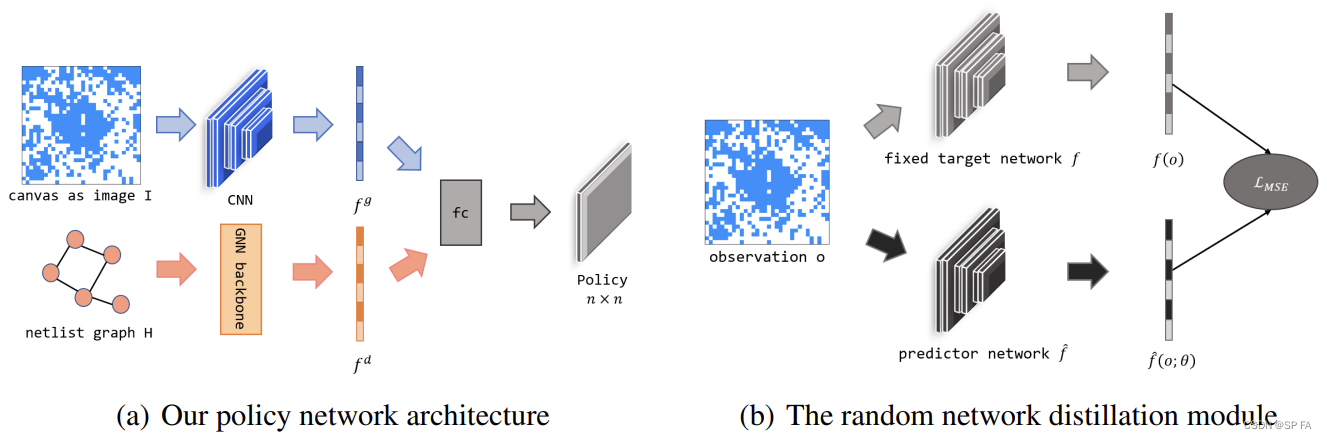
[读论文] On Joint Learning for Solving Placement and Routing in Chip Design
0. Abstract 由于 GPU 在加速计算方面的优势和对人类专家的依赖较少,机器学习已成为解决布局和布线问题的新兴工具,这是现代芯片设计流程中的两个关键步骤。它仍处于早期阶段,存在一些基本问题:可扩展性、奖励设计和端到端学习范…...

L2-1 插松枝
L2-1 插松枝 分数 25 全屏浏览题目 切换布局 作者 陈越 单位 浙江大学 人造松枝加工场的工人需要将各种尺寸的塑料松针插到松枝干上,做成大大小小的松枝。他们的工作流程(并不)是这样的: 每人手边有一只小盒子,初始…...

Android 使用ContentObserver监听SettingsProvider值的变化
1、Settings原理 Settings 设置、保存的一些值,最终是存储到 SettingsProvider 的数据库 例如: Settings.Global.putInt(getContentResolver(), "SwitchLaunch", 0); Settings.System.putInt(getContentResolver(), "SwitchLaunch&quo…...
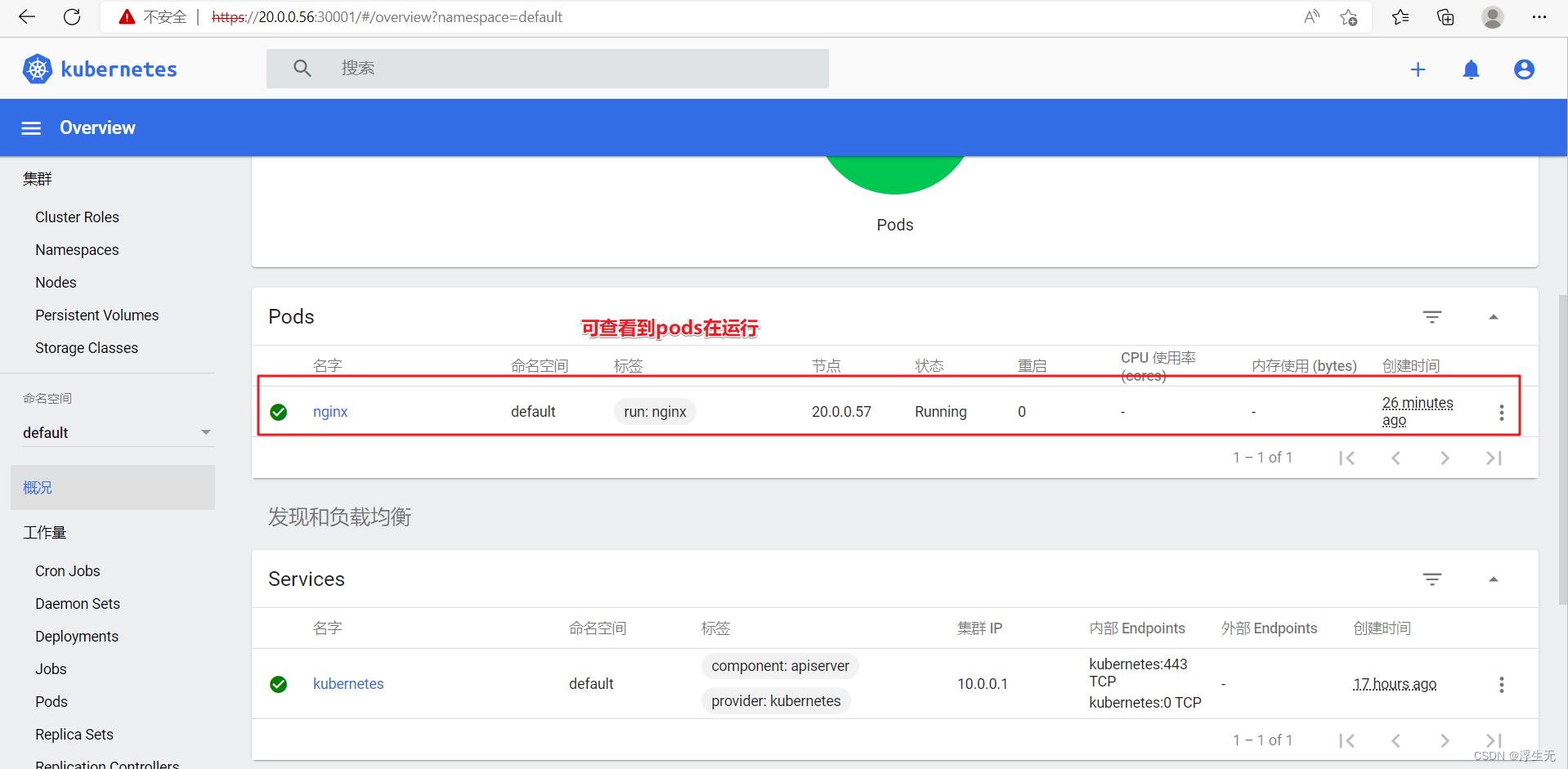
二进制安装部署k8s
概要 常见的K8S按照部署方式 minikube 是一个工具,可以在本地快速运行一个单节点微型K8S,仅用于学习,预习K8S的一些特性使用。 Kubeadmin kubeadmin也是一个工具,特工kubeadm init 和kubedm join,用于快速部署k8s…...
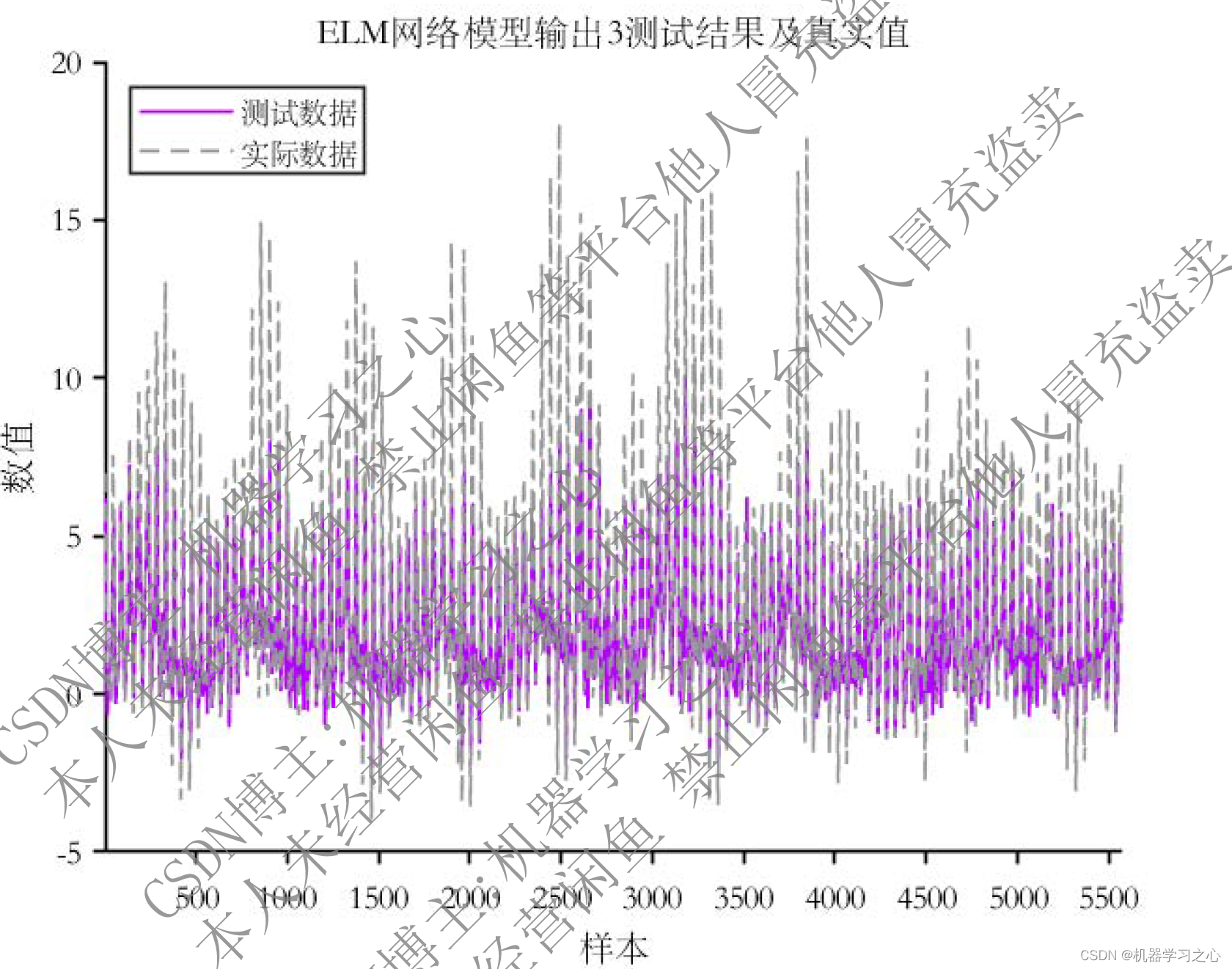
多输入多输出 | Matlab实现k-means-ELM(k均值聚类结合极限学习机)多输入多输出组合预测
多输入多输出 | Matlab实现k-means-ELM(k均值聚类结合极限学习机)多输入多输出组合预测 目录 多输入多输出 | Matlab实现k-means-ELM(k均值聚类结合极限学习机)多输入多输出组合预测预测效果基本描述程序设计参考资料 预测效果 基…...

ITSource 分享 第5期【校园信息墙系统】
项目介绍 本期给大家介绍一个 校园信息墙 系统,可以发布信息,表白墙,分享墙,校园二手买卖,咨询分享等墙信息。整个项目还是比较系统的,分为服务端,管理后台,用户Web端,小…...
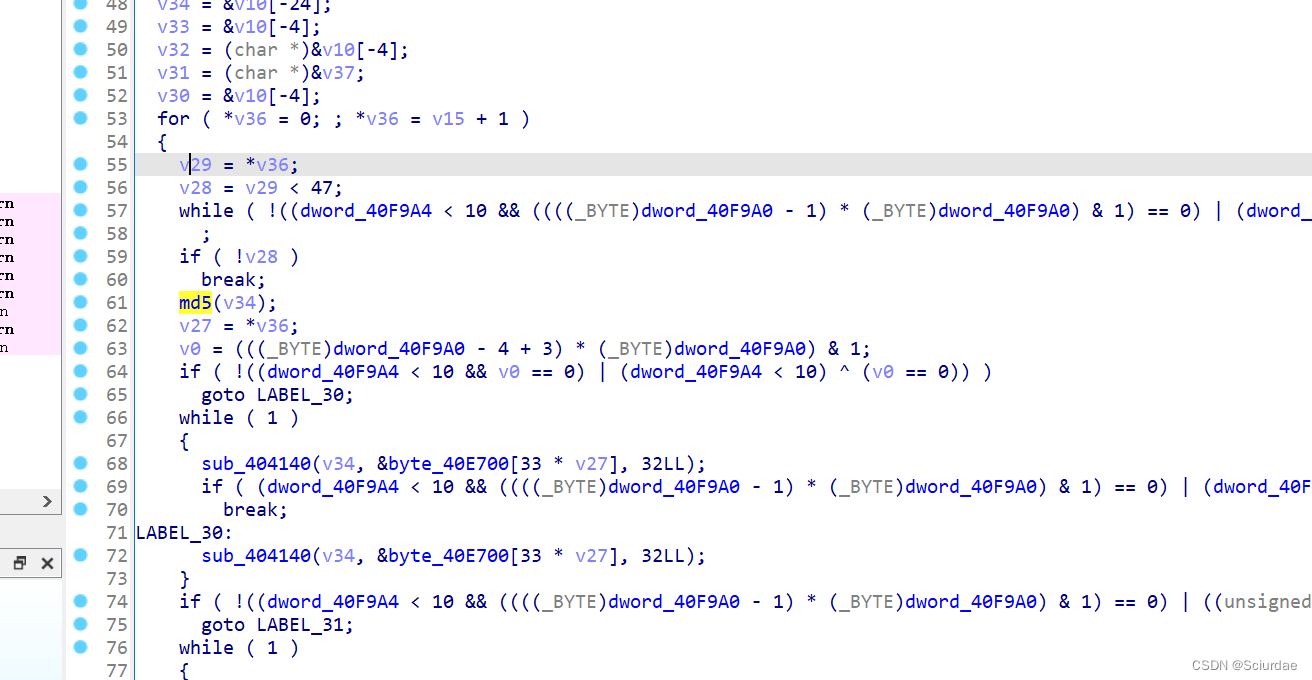
记 : CTF2023羊城杯 - Reverse 方向 Blast 题目复现and学习记录
文章目录 前言题目分析and复习过程exp 前言 羊城杯题目复现: 第一题 知识点 :DES算法 : 链接:Ez加密器 第二题 知识点 :动态调试 : 链接:CSGO 这一题的查缺补漏: 虚假控制流的去除…...

【数据结构练习题】删除有序数组中的重复项
✨博客主页:小钱编程成长记 🎈博客专栏:数据结构练习题 🎈相关博文:消失的数字 — 三种解法超详解 删除有序数组中的重复项 1.🎈题目2. 🎈解题思路3. 🎈具体代码🎇总结 1…...
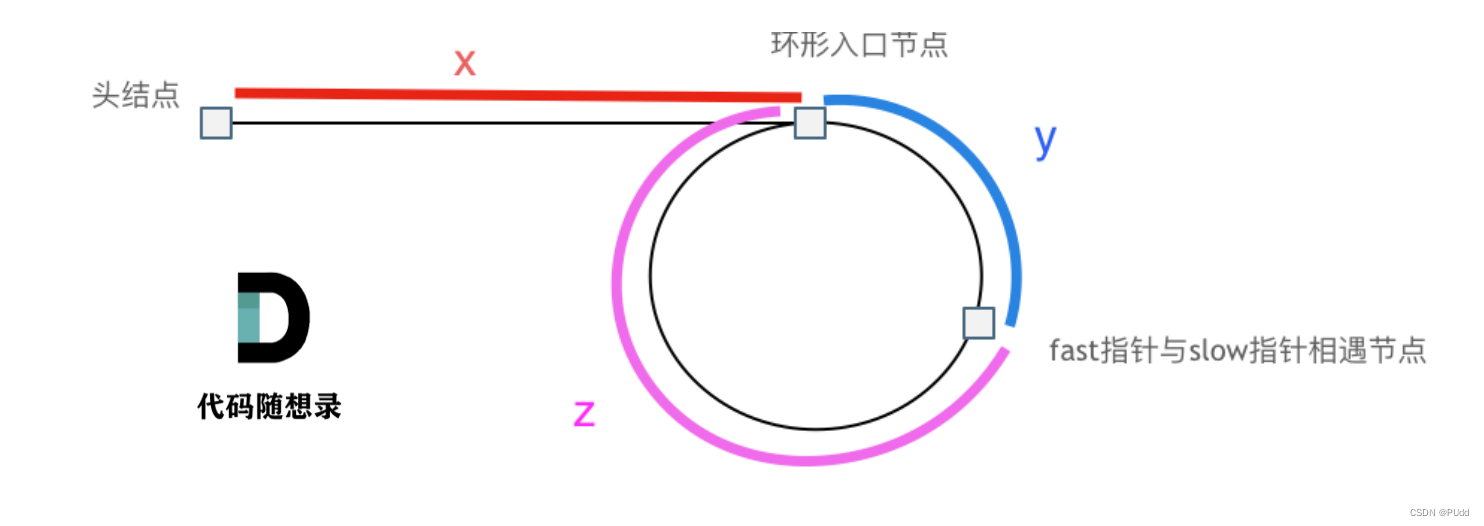
leetcode-链表
链表是一个用指针串联起来的线性结构,每个结点由数据域和指针域构成,指针域存放的是指向下一个节点的指针,最后一个节点指向NULL,第一个结点称为头节点head。 常见的链表有单链表、双向链表、循环链表。双向链表就是多了一个pre指…...
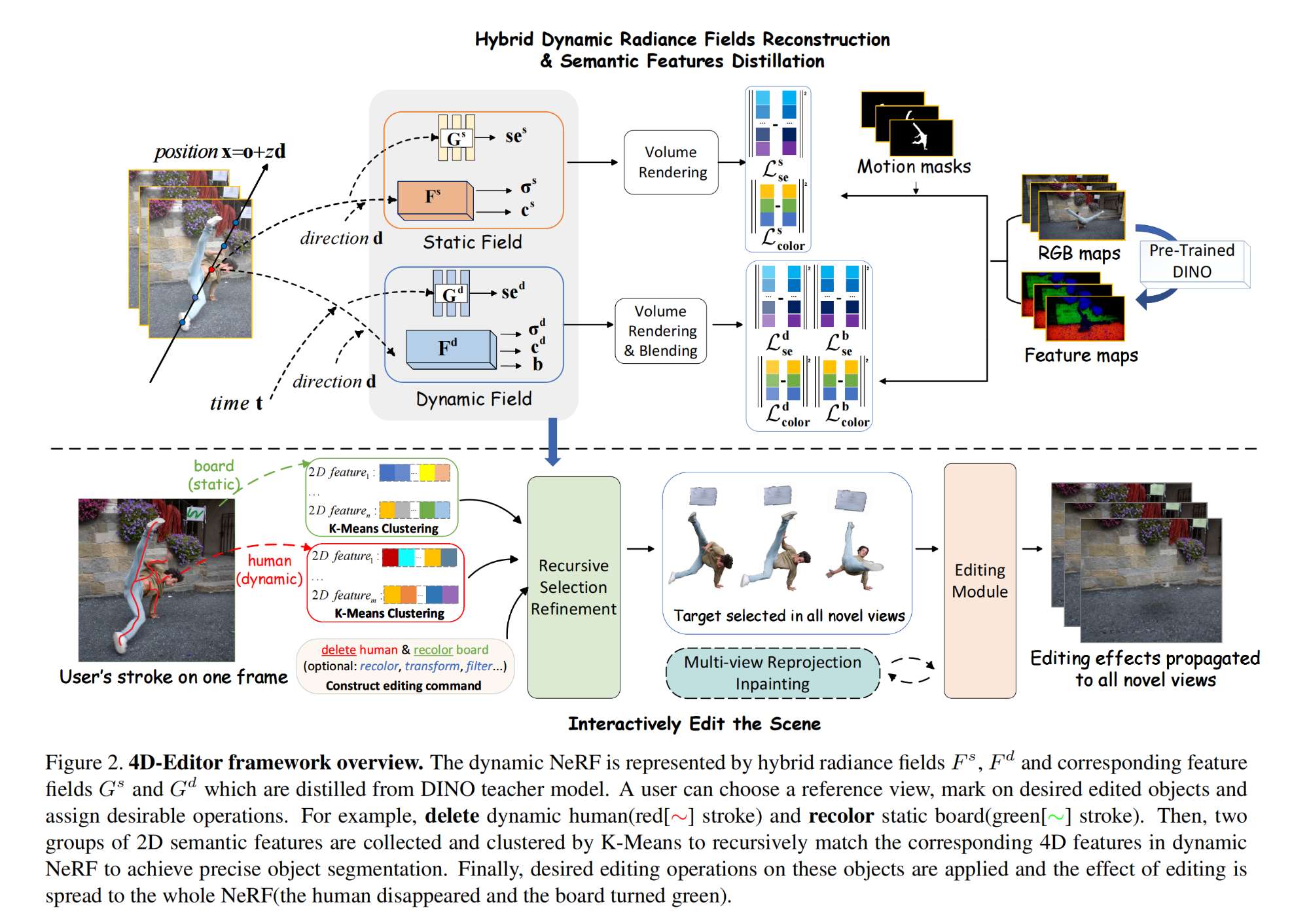
CV计算机视觉每日开源代码Paper with code速览-2023.10.27
精华置顶 墙裂推荐!小白如何1个月系统学习CV核心知识:链接 点击CV计算机视觉,关注更多CV干货 论文已打包,点击进入—>下载界面 点击加入—>CV计算机视觉交流群 1.【基础网络架构:Transformer】(Ne…...
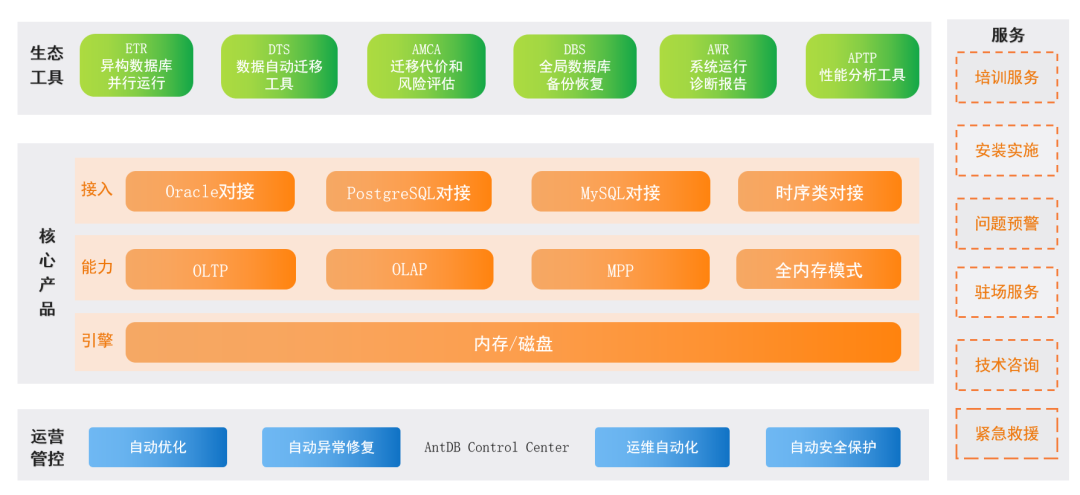
“赋能信创,物联未来” AntDB数据库携高可用解决方案亮相2023世界数字经济大会
10月14日,在2023世界数字经济大会暨京甬信创物联网产融对接会上,AntDB数据库技术总监北陌应邀发表《AntDB国产分布式数据库创新演进与高可用解决方案》主题演讲,就AntDB数据库助力客户数智化升级的高可用信创解决方案进行了详实、真挚地分享&…...
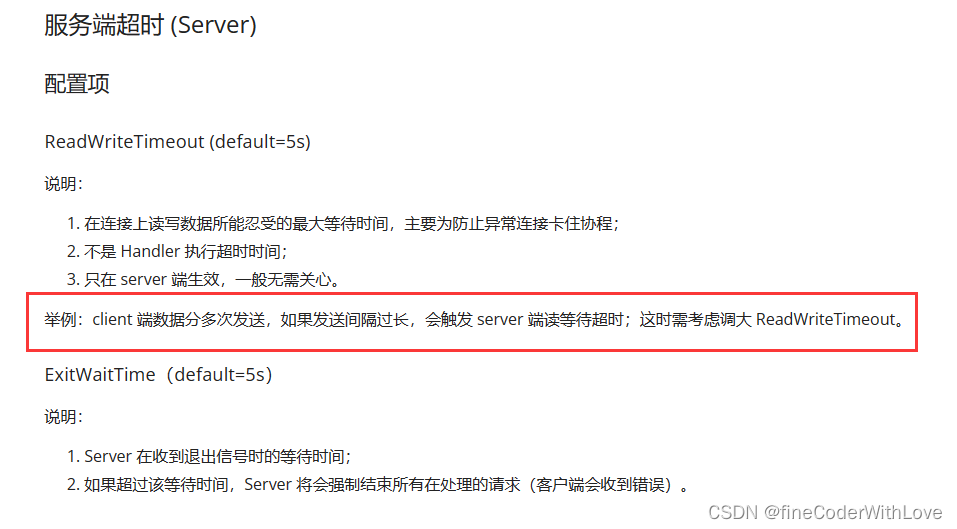
Kitex踩坑 [Error] KITEX: processing request error,i/o timeout
报错问题 2023/010/28 17:20:10.250768 default_server_handler.go:234: [Error] KITEX: processing request error, remoteService, remoteAddr127.0.0.1:65425, errordefault codec read failed: read tcp 127.0.0.1:8888->127.0.0.1:65425: i/o timeout 分析原因 Hert…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...

作为测试我们应该关注redis哪些方面
1、功能测试 数据结构操作:验证字符串、列表、哈希、集合和有序的基本操作是否正确 持久化:测试aof和aof持久化机制,确保数据在开启后正确恢复。 事务:检查事务的原子性和回滚机制。 发布订阅:确保消息正确传递。 2、性…...

用递归算法解锁「子集」问题 —— LeetCode 78题解析
文章目录 一、题目介绍二、递归思路详解:从决策树开始理解三、解法一:二叉决策树 DFS四、解法二:组合式回溯写法(推荐)五、解法对比 递归算法是编程中一种非常强大且常见的思想,它能够优雅地解决很多复杂的…...

深入解析光敏传感技术:嵌入式仿真平台如何重塑电子工程教学
一、光敏传感技术的物理本质与系统级实现挑战 光敏电阻作为经典的光电传感器件,其工作原理根植于半导体材料的光电导效应。当入射光子能量超过材料带隙宽度时,价带电子受激发跃迁至导带,形成电子-空穴对,导致材料电导率显著提升。…...
Element-Plus:popconfirm与tooltip一起使用不生效?
你们好,我是金金金。 场景 我正在使用Element-plus组件库当中的el-popconfirm和el-tooltip,产品要求是两个需要结合一起使用,也就是鼠标悬浮上去有提示文字,并且点击之后需要出现气泡确认框 代码 <el-popconfirm title"是…...
