如何从Android手机上轻松恢复误删除的短信 ?
当您使用 Android 手机时,您可能会误删除一些 Android 短信。如果这些消息对您很重要,您可能想要恢复它们。在这种情况下,您可以尝试使用U1tData安卓数据恢复(奇客软件) 来完成这项工作。这篇文章将向您展示更多信息。
删除的安卓短信还能恢复吗?
如上所述,有很多原因可能导致 Android 短信丢失。当您遇到此问题时,您一定想知道:Android 是否可以恢复已删除的短信?
首先需要确保安卓设备在手上,并且可以正常开机。
然后,只要删除的安卓短信没有被新数据覆盖,就可以使用一款安卓专用数据恢复软件来恢复删除的安卓短信。但是,哪个软件是最好的选择?
您需要尽快取回已删除的 Android 联系人是正确的,因为一旦已删除的 Android 短信被新数据覆盖,它们将无法恢复。
因此,一旦您决定恢复删除短信 Android,请尽快停止使用您的 Android 设备。
当您在互联网上搜索 Android 数据恢复软件问题时,您一定会眼花缭乱,因为那里列出了众多工具,而且他们都声称可以找回已删除的 Android 数据。您需要一一尝试吗?
并不真地。在这种情况下,您应该试试这个工具 - U1tData安卓数据恢复(奇客软件),它不会让您失望的。
如何恢复已删除的短信 Android
U1tData安卓数据恢复(奇客软件)为您提供两个恢复模块。使用这恢复模块,您可以从 Android 手机和平板电脑以及 SD 卡中恢复已删除和丢失的 Android 数据。
安卓数据恢复-奇客官网免费下载Android数据恢复软件扫描数据,支持文件、照片、视频、邮件、音频、微信消息等1000+种文件格式。![]() https://www.geekersoft.cn/geekersoft-recovergo-android.html
https://www.geekersoft.cn/geekersoft-recovergo-android.html
恢复的数据类型多种多样,包括文本数据,例如短信,联系人,通话记录,微信和文档数据;照片、APP 照片、视频、音频、微信附件等媒体数据。

所以这款软件完全可以满足您对安卓短信的恢复需求。幸运的是,该软件的免费版允许您恢复一种文件类型的 10 个文件。
一切准备就绪后,您可以将 Android 手机连接到计算机并开始 Android 消息恢复过程。在这篇文章中,我们将向您展示如何从小米手机中检索已删除的短信。
第 1 步:双击打开软件图标,进入软件主界面。要恢复已删除的短信 Android,您应该单击从电话模块恢复以继续。
第 2 步:该软件将开始直接分析您的 Android 手机。这个过程很快,如果你没有允许从这台电脑进行USB调试,你会进入下面的界面。
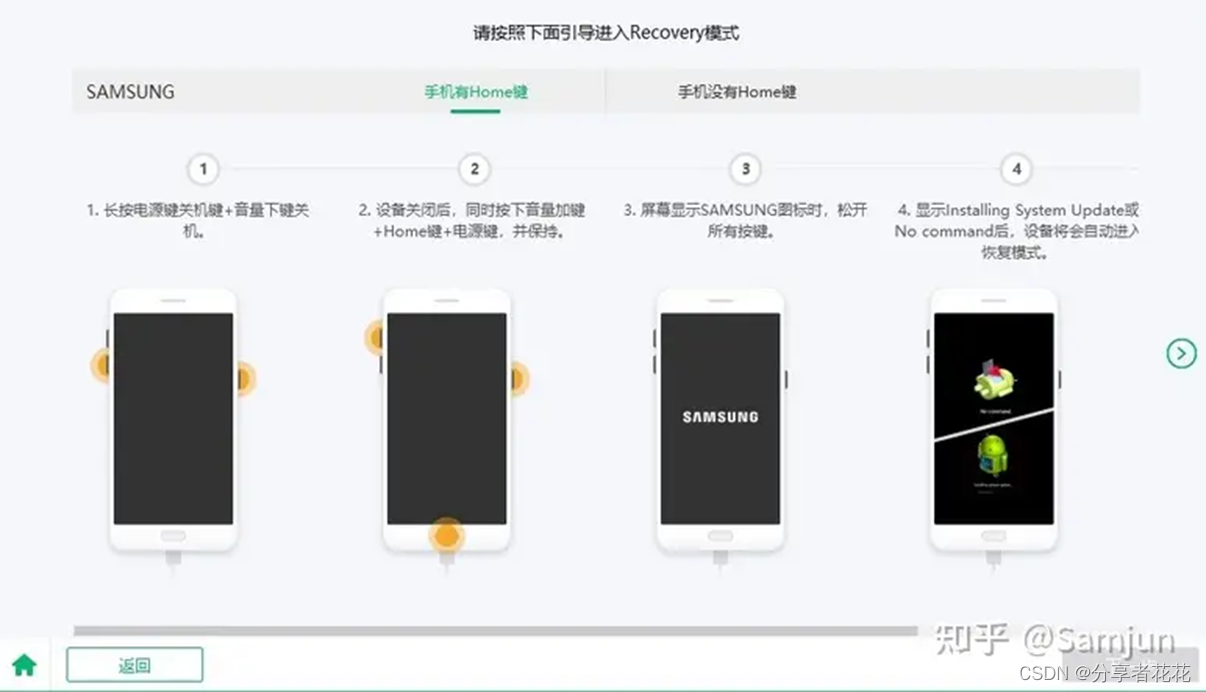
如果你的安卓手机没有开启USB调试,分析完后你会看到如下界面。
在这里,您应该注意不同的 Android 版本有不同的步骤来启用 USB 调试。请在该界面选择对应的安卓版本,按照提示开启USB调试。
第 3 步:然后你会进入这个扫描界面,如下图。在此界面中,您可以看到顶部列出了该软件可以恢复的文件类型,其次是两种扫描方式。
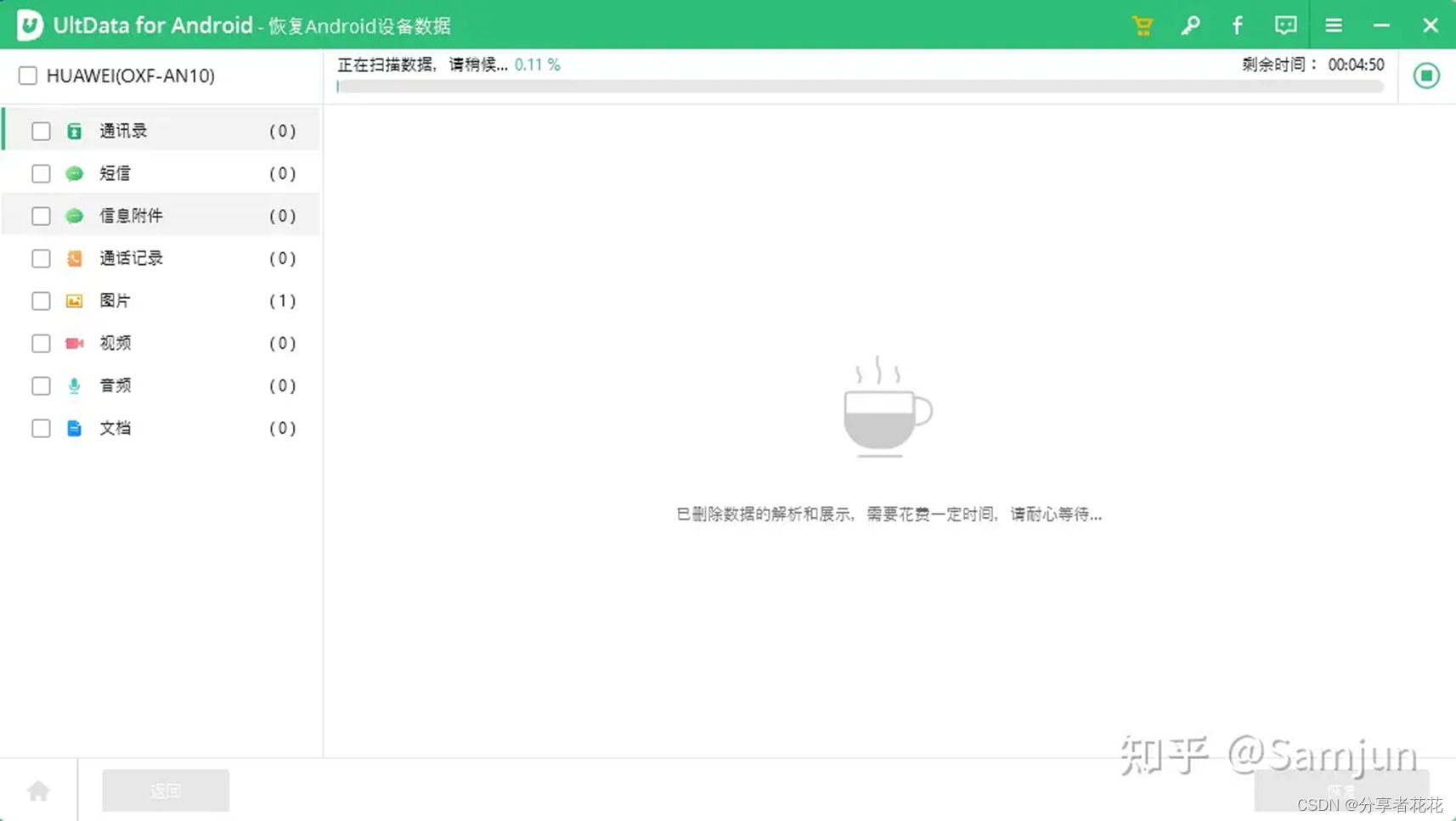
在阅读了这两种扫描方法的详细介绍后,您可以看到快速扫描方法是您检索已删除的 Android 短信的选择。只需检查它并单击右下侧蓝色按钮下一步继续。
第 4 步:该软件将首先开始分析您的 Android 手机,然后扫描您的 Android 设备。当这两个过程完成后,您可以进入其扫描结果界面,如下所示。

然后,只需检查您要检索的项目,然后单击“恢复”按钮继续。
最后,你想要的安卓短信就保存到指定的存储路径中了。在这里,您可以打开该文件夹并直接查看这些恢复的项目。
结论
在这篇文章中,我们向您介绍如何使用U1tData安卓数据恢复(奇客软件)来取消删除 Android 消息。
使用此工具的“从手机恢复”模块,您可以轻松扫描您的 Android 设备,找到您的 Android 数据,选择您要恢复的项目,然后将它们保存到您的计算机。
恢复已删除短信常见问题解答
我可以恢复已删除的短信 Android 吗?
如果您已经在 Android 上备份了您的短信,您可以从之前的备份中恢复它们。否则,您将需要使用第三方 Android 数据恢复软件U1tData安卓数据恢复(奇客软件)来找回它们。
如何在没有电脑的情况下从我的 Android 设备中检索已删除的短信?
一些Android 恢复 APK可用于在没有计算机的情况下恢复 Android 删除的短信。但我们不建议这样做,因为 Android 恢复 APK 可能会覆盖已删除的短信并使它们无法恢复。我们仍然认为您应该使用U1tData安卓数据恢复(奇客软件)来尝试一下。
我可以找回已删除的短信吗?
如果删除的短信被新数据完全覆盖,您只能从可用的备份文件中恢复它们。
Google 会备份短信吗?
Google 不会备份您的短信。如果你想备份你的安卓短信,你可以搜索一些专门的安卓短信备份软件来完成这项工作。
相关文章:

如何从Android手机上轻松恢复误删除的短信 ?
当您使用 Android 手机时,您可能会误删除一些 Android 短信。如果这些消息对您很重要,您可能想要恢复它们。在这种情况下,您可以尝试使用U1tData安卓数据恢复(奇客软件) 来完成这项工作。这篇文章将向您展示更多信息。…...

毅速丨金属3D打印能替代传统制造吗?
金属3D打印技术已经逐渐被很多行业认可和应用,但是目前,金属3D打印多数被作为传统制造技术的一种补充,暂时还不能完全替代传统制造。 金属3D打印使用的是金属粉末进行选择性激光烧结,打印时在成型缸里铺上金属粉末,打印…...

21个新的ChatGPT应用
自从GPT有了图识别功能后变的更加强大,特别是ChatGPT的视觉技术,为我们提供了无数的可能性。本文将深入探讨这21种应用场景,帮助理解其在日常生活和工作中的实际价值。 生活助手:为日常生活增添色彩 健身计划定制:你…...

【通信原理】第二章|确知信号
前言 那么这里博主先安利一些干货满满的专栏了! 首先是博主的高质量博客的汇总,这个专栏里面的博客,都是博主最最用心写的一部分,干货满满,希望对大家有帮助。 高质量博客汇总 文章目录 前言 第二章 确知信号1. 确知…...
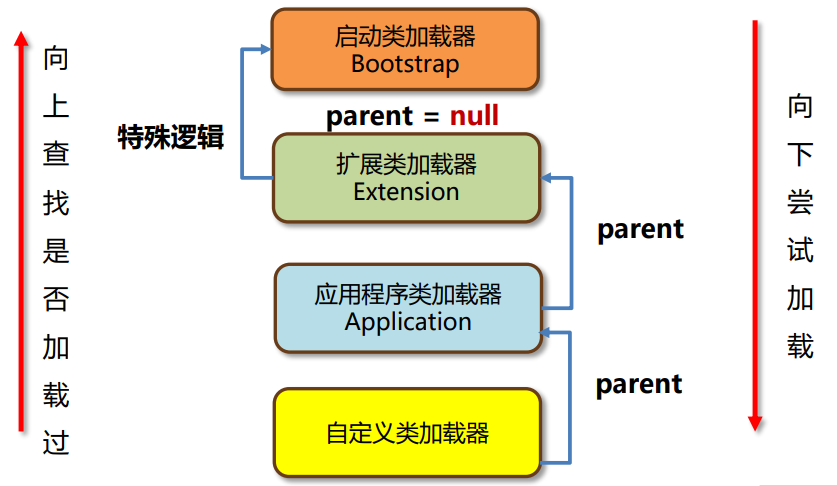
【JVM】类加载器
【JVM】类加载器 文章目录 【JVM】类加载器0. 类加载器概述1. 类加载器的分类1.1 启动类加载器1.2 Java中的默认类加载器1.2.1 扩展类加载器1.2.2 应用程序类加载器 2. 双亲委派机制2.1 类的双亲委派机制是什么?2.2 打破双亲委派机制2.2.1 自定义类加载器2.2.2 线程…...
利用Excel支持JUnit参数化测试
在JUnit里面,可以使用CsvFileSource读取csv文件进行参数化测试,可是CSV文件不支持格式,编辑颇为麻烦,尤其是多次编辑,因此自然想到是否可以使用Excel文件,可以有各种格式,支持各类数据。 最新开…...
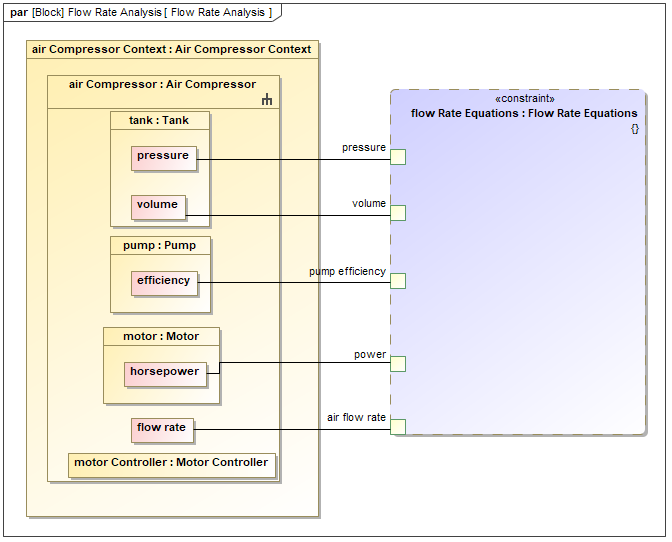
第三章 SysML入门|系统建模语言SysML实用指南学习
仅供个人学习记录 UML与SysML的联系 可以稍微参考UML与SysML的联系 UML(统一建模语言)和SysML(系统建模语言)是两种与建模相关的语言,它们之间存在联系和区别。 SysML的图分类如下图所示。 SysML 图概述 这里只…...

敏捷开发框架Scrum-概述
如果你是一个程序员,可能会觉得这是个程序开发框架。Scrum是一个敏捷开发框架。我们可以把Scrum理解成一个团队一次完成一小部分工作的方式。这种方式通过不断的实验和反馈循环来学习和改进。Scrum可以帮助团队以协作的方式逐步交付价值。 Scrum框架由一个Scrum团队…...

Hafnium启动过程分析
安全之安全(security)博客目录导读 目录 一、在安全世界中加载Hafnium和安全分区 二、通过TF-A启动 1、SP manifests 2、安全分区包 3、描述安全分区...
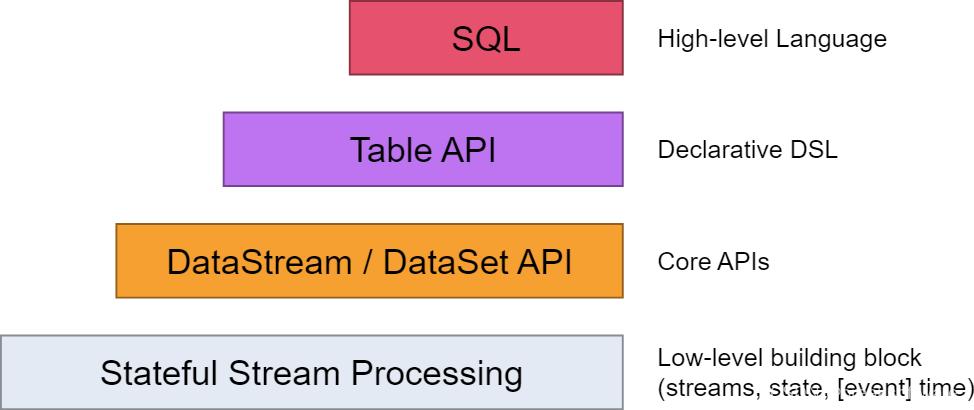
0基础学习PyFlink——使用Table API实现SQL功能
大纲 Souceschemadescriptor Sinkschemadescriptor Execute完整代码参考资料 《0基础学习PyFlink——使用PyFlink的Sink将结果输出到Mysql》一文中,我们讲到如何通过定义Souce、Sink和Execute三个SQL,来实现数据读取、清洗、计算和入库。 如下图所示SQL是最高层级的…...
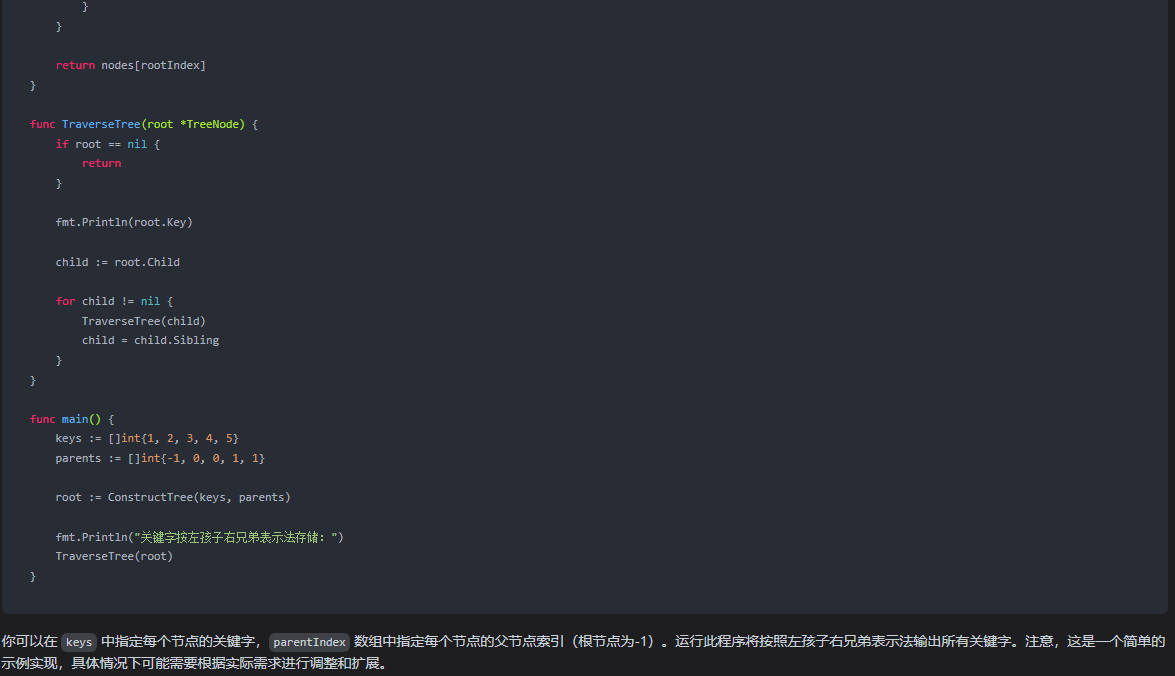
文心一言 VS 讯飞星火 VS chatgpt (123)-- 算法导论10.4 4题
四、用go语言,对于一个含 n个结点的任意有根树,写出一个 O(n)时间的过程,输出其所有关键字该树以左孩子右兄弟表示法存储。 文心一言: 在计算机科学中,左孩子右兄弟表示法是一种用于表示树状结构的方法,其…...
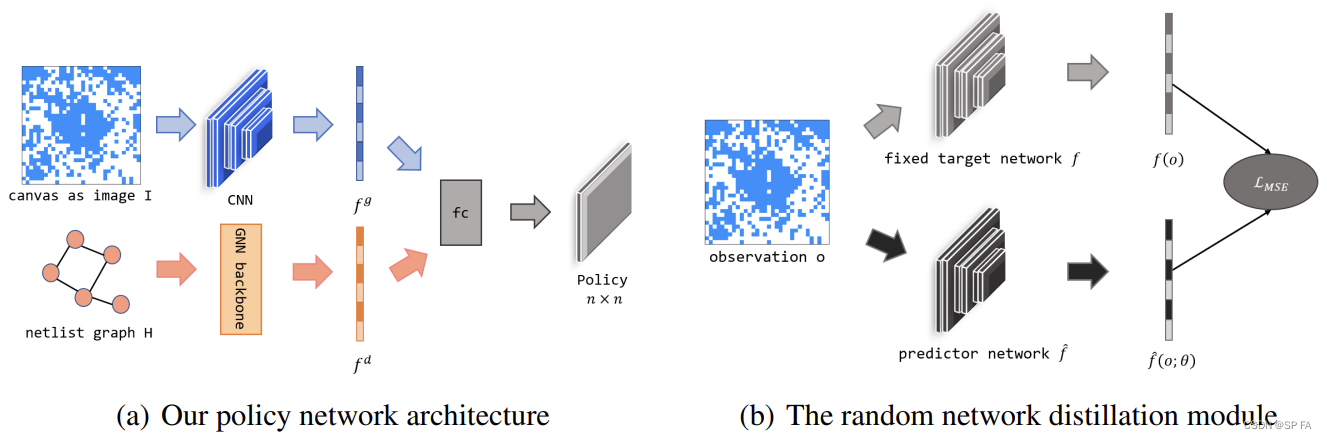
[读论文] On Joint Learning for Solving Placement and Routing in Chip Design
0. Abstract 由于 GPU 在加速计算方面的优势和对人类专家的依赖较少,机器学习已成为解决布局和布线问题的新兴工具,这是现代芯片设计流程中的两个关键步骤。它仍处于早期阶段,存在一些基本问题:可扩展性、奖励设计和端到端学习范…...

L2-1 插松枝
L2-1 插松枝 分数 25 全屏浏览题目 切换布局 作者 陈越 单位 浙江大学 人造松枝加工场的工人需要将各种尺寸的塑料松针插到松枝干上,做成大大小小的松枝。他们的工作流程(并不)是这样的: 每人手边有一只小盒子,初始…...

Android 使用ContentObserver监听SettingsProvider值的变化
1、Settings原理 Settings 设置、保存的一些值,最终是存储到 SettingsProvider 的数据库 例如: Settings.Global.putInt(getContentResolver(), "SwitchLaunch", 0); Settings.System.putInt(getContentResolver(), "SwitchLaunch&quo…...
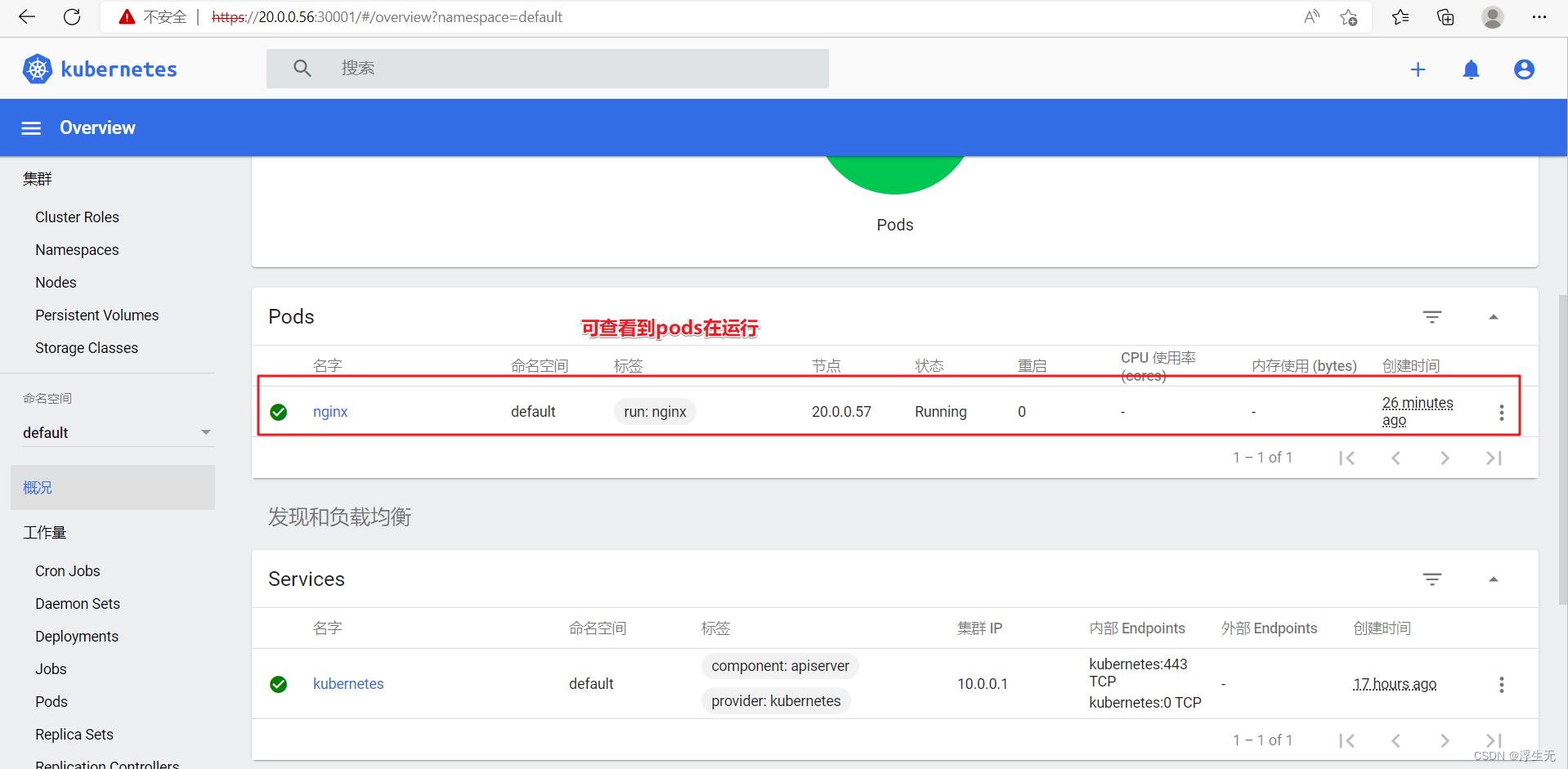
二进制安装部署k8s
概要 常见的K8S按照部署方式 minikube 是一个工具,可以在本地快速运行一个单节点微型K8S,仅用于学习,预习K8S的一些特性使用。 Kubeadmin kubeadmin也是一个工具,特工kubeadm init 和kubedm join,用于快速部署k8s…...
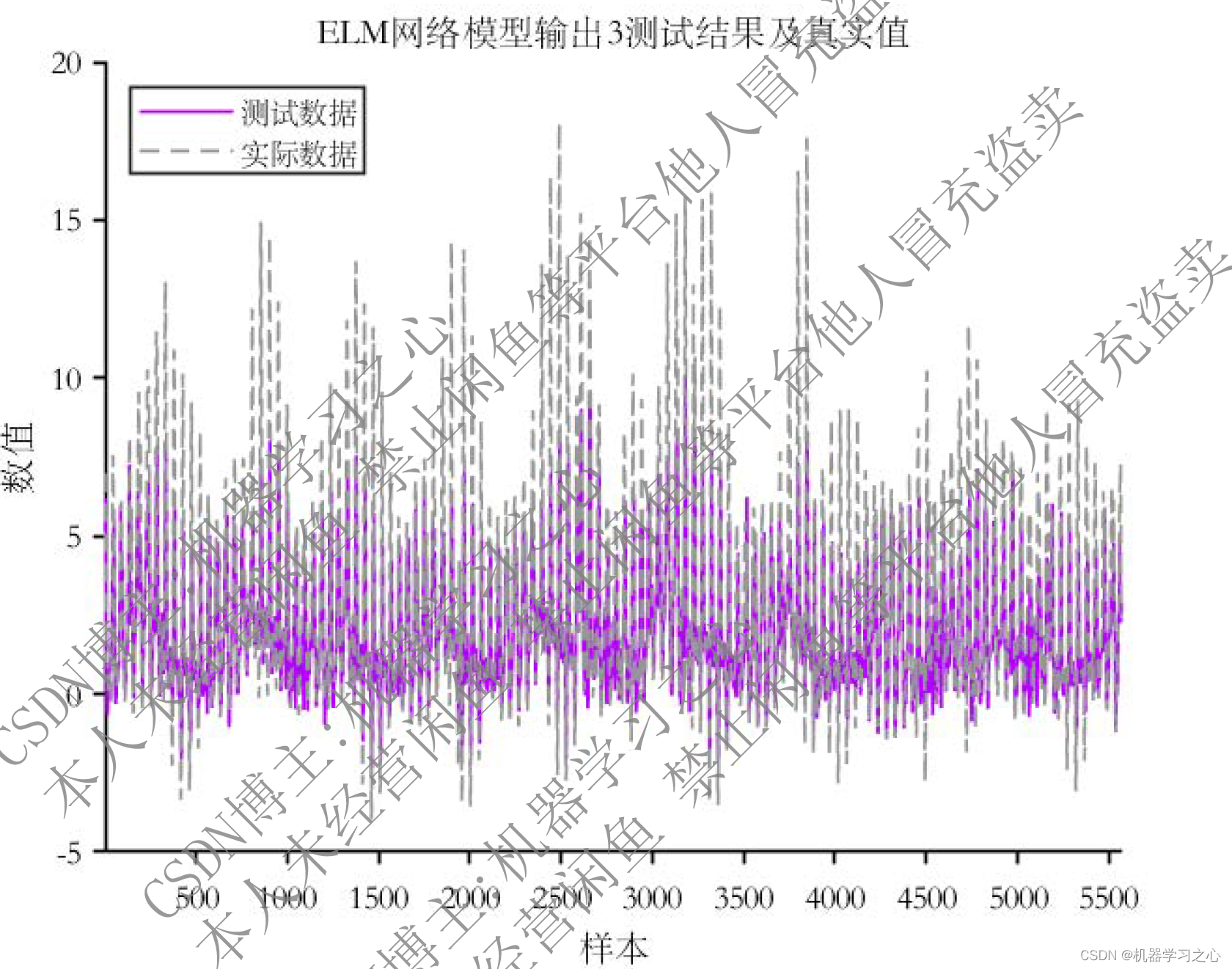
多输入多输出 | Matlab实现k-means-ELM(k均值聚类结合极限学习机)多输入多输出组合预测
多输入多输出 | Matlab实现k-means-ELM(k均值聚类结合极限学习机)多输入多输出组合预测 目录 多输入多输出 | Matlab实现k-means-ELM(k均值聚类结合极限学习机)多输入多输出组合预测预测效果基本描述程序设计参考资料 预测效果 基…...

ITSource 分享 第5期【校园信息墙系统】
项目介绍 本期给大家介绍一个 校园信息墙 系统,可以发布信息,表白墙,分享墙,校园二手买卖,咨询分享等墙信息。整个项目还是比较系统的,分为服务端,管理后台,用户Web端,小…...
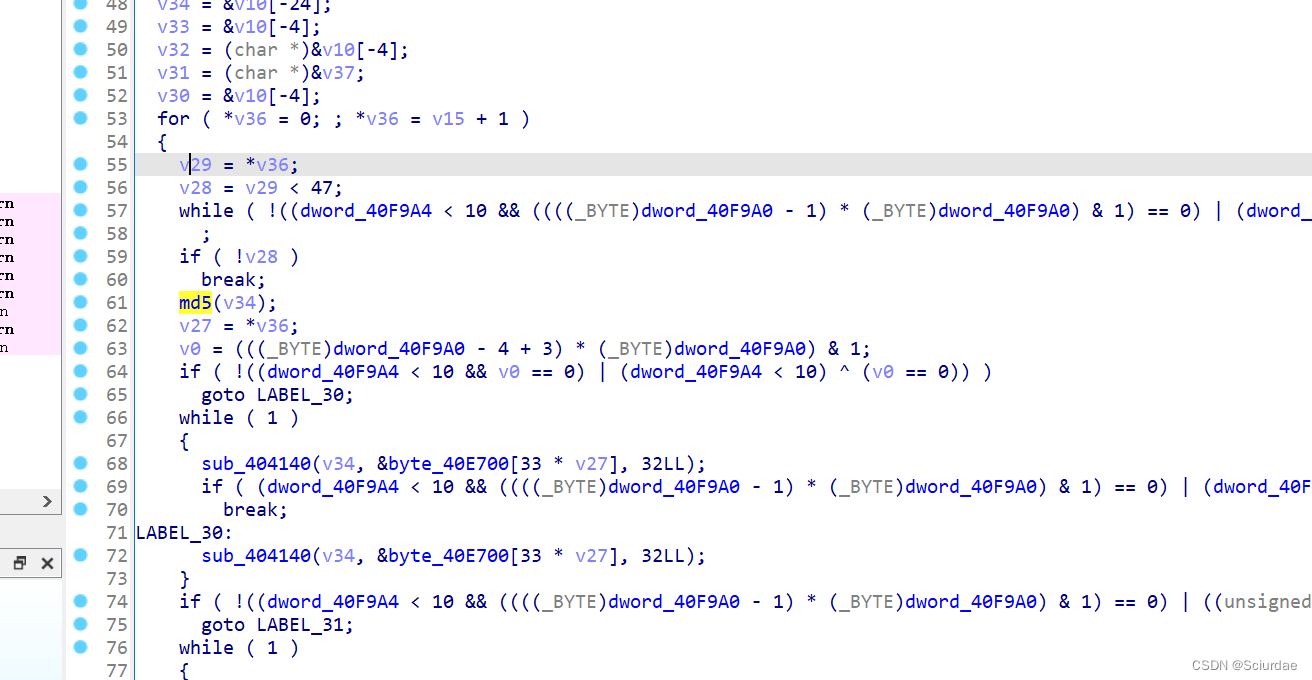
记 : CTF2023羊城杯 - Reverse 方向 Blast 题目复现and学习记录
文章目录 前言题目分析and复习过程exp 前言 羊城杯题目复现: 第一题 知识点 :DES算法 : 链接:Ez加密器 第二题 知识点 :动态调试 : 链接:CSGO 这一题的查缺补漏: 虚假控制流的去除…...

【数据结构练习题】删除有序数组中的重复项
✨博客主页:小钱编程成长记 🎈博客专栏:数据结构练习题 🎈相关博文:消失的数字 — 三种解法超详解 删除有序数组中的重复项 1.🎈题目2. 🎈解题思路3. 🎈具体代码🎇总结 1…...
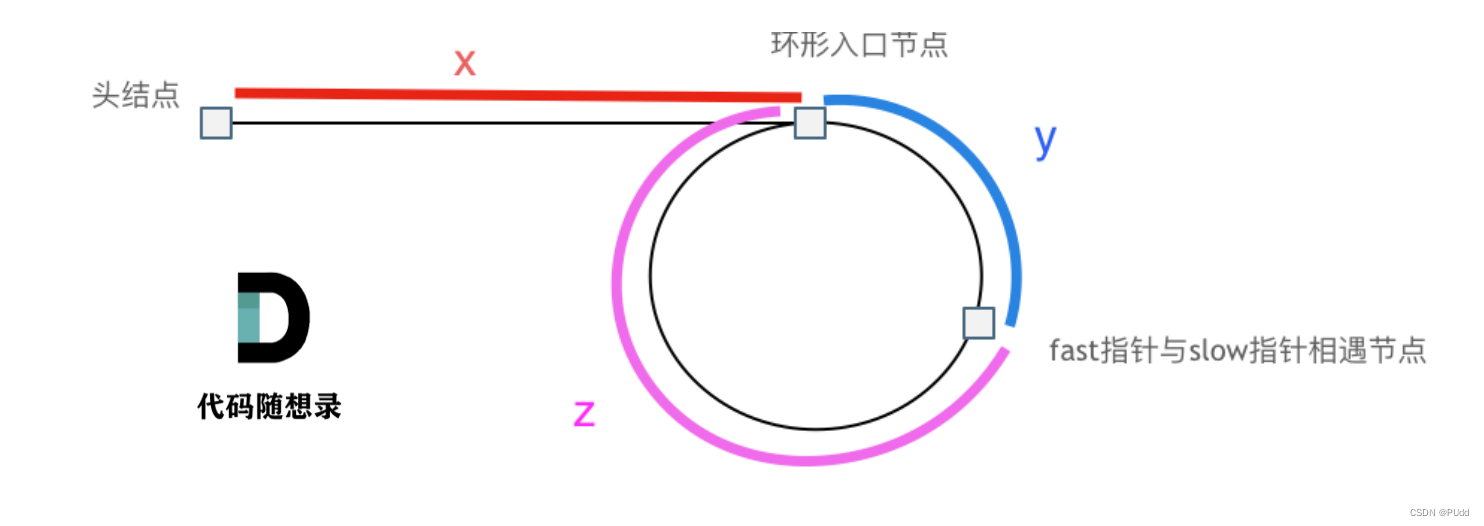
leetcode-链表
链表是一个用指针串联起来的线性结构,每个结点由数据域和指针域构成,指针域存放的是指向下一个节点的指针,最后一个节点指向NULL,第一个结点称为头节点head。 常见的链表有单链表、双向链表、循环链表。双向链表就是多了一个pre指…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...

基于Springboot+Vue的办公管理系统
角色: 管理员、员工 技术: 后端: SpringBoot, Vue2, MySQL, Mybatis-Plus 前端: Vue2, Element-UI, Axios, Echarts, Vue-Router 核心功能: 该办公管理系统是一个综合性的企业内部管理平台,旨在提升企业运营效率和员工管理水…...

MySQL 索引底层结构揭秘:B-Tree 与 B+Tree 的区别与应用
文章目录 一、背景知识:什么是 B-Tree 和 BTree? B-Tree(平衡多路查找树) BTree(B-Tree 的变种) 二、结构对比:一张图看懂 三、为什么 MySQL InnoDB 选择 BTree? 1. 范围查询更快 2…...

解析奥地利 XARION激光超声检测系统:无膜光学麦克风 + 无耦合剂的技术协同优势及多元应用
在工业制造领域,无损检测(NDT)的精度与效率直接影响产品质量与生产安全。奥地利 XARION开发的激光超声精密检测系统,以非接触式光学麦克风技术为核心,打破传统检测瓶颈,为半导体、航空航天、汽车制造等行业提供了高灵敏…...

多元隐函数 偏导公式
我们来推导隐函数 z z ( x , y ) z z(x, y) zz(x,y) 的偏导公式,给定一个隐函数关系: F ( x , y , z ( x , y ) ) 0 F(x, y, z(x, y)) 0 F(x,y,z(x,y))0 🧠 目标: 求 ∂ z ∂ x \frac{\partial z}{\partial x} ∂x∂z、 …...
