2.2 消元法的概念
一、消元法介绍
消元法(elimination)是一个求解线性方程组的系统性方法。下面是使用消元法求解一个 2 × 2 2\times2 2×2 线性方程组的例子。消元之前,两个方程都有 x x x 和 y y y,消元后,第一个未知数 x x x 将从第二个方程消失:

新的方程 8 y = 8 8y=8 8y=8 能够直接得到 y = 1 y=1 y=1,再将 y = 1 y=1 y=1 回代到第一个方程 x − 2 y = 1 x-2y=1 x−2y=1,求得 x = 3 x=3 x=3,则解就是 ( x , y ) = ( 3 , 1 ) (x,y)=(3,1) (x,y)=(3,1)。
消元法的目的是得到一个上三角形系统。非零系数 1 , − 2 , 8 1,-2,8 1,−2,8 形成一个三角形,这个系统从底部向上求解。首先得到 y = 1 y=1 y=1,然后求得 x = 3 x=3 x=3。这个过程称之为回代。经过消元法得到的三角形,回代可以在任意大小(行和列)的上三角形上使用。
重点: 原始方程组有着相同的解 x = 3 , y = 1 x=3,y=1 x=3,y=1。Figure 2.5 中对这两个系统都使用了一对直线来表示,它们均相交于点 ( 3 , 1 ) (3,1) (3,1)。即经过消元后,它们会交于相同的点,每一步的方程都有相同的解。

如何从第一对直线得到第二对直线呢?将第一个方程乘 3 3 3,然后用第二个方程减去第一个方程。目的是消去未知数 x x x:
消去 x x x:从方程 2 2 2 减去方程 1 1 1 的倍数
3 3 3 乘 x − 2 y = 1 x-2y=1 x−2y=1 得到 3 x − 6 y = 3 3x-6y=3 3x−6y=3,从方程 3 x + 2 y = 11 3x+2y=11 3x+2y=11 减去上面的方程,右侧得到 8 8 8,重点是左侧 3 x 3x 3x 与 3 x 3x 3x 相消得到 2 y − ( − 6 y ) = 8 y 2y-(-6y)=8y 2y−(−6y)=8y,消去了 x x x,系统变成了三角形。
如何得到乘数 l = 3 l=3 l=3 呢?第一个方程包含 1 x 1x 1x,所以第一个主元是 1 1 1( x x x 的系数),第二个方程包含 3 x 3x 3x,所以乘数是 3 3 3。 3 x − 3 x 3x-3x 3x−3x 就可以得到零和三角形。
如果将第一个方程变为 4 x − 8 y = 4 4x-8y=4 4x−8y=4(同样的直线,但是第一个主元变成 4 4 4)。现在乘数就变成了 l = 3 / 4 l=3/4 l=3/4。把需要消去的系数 3 3 3 除以主元 4 4 4 就可以得到乘数:

最终仍然是个三角形系统,通过最后一个方程得到 y = 1 y=1 y=1。回代后得到 4 x − 8 = 4 4x-8=4 4x−8=4,解得 x = 3 x=3 x=3。这里虽然改变了数字,但是直线是不变的,解也就不会变。
主元 = 经过消元后的行的第一个非零数 乘数 = (需要消去的元) / (主元) = 3 / 4 \pmb{主元} = 经过消元后的行的第一个非零数\kern 15pt\\ \pmb{乘数} = (需要消去的元)/(主元)= 3/4 主元=经过消元后的行的第一个非零数乘数=(需要消去的元)/(主元)=3/4
新的第二个方程是从第二主元开始的,主元是 8 8 8。如果要解 n n n 个方程,那么需要 n n n 个主元,完成消元后,这些主元都会在三角形的对角线上。
二、消元法失效
正常情况下消元法可以找到解,但是也有失效的情况。有时会遇到除以 0 0 0 的情况,这种情况下可能需要调整顺序,也可能消元法完全失效。
一般有如下三种例题的情况:例 1 是无解的情况,例 2 是有无穷解,例 3 可以通过交换方程的顺序来解决。
【例1】无解而完全失效。消元过后可以清楚的看到: x − 2 y = 1 3 x − 6 y = 11 消元后 x − 2 y = 1 0 y = 8 \begin{matrix}x-2y=1\\3x-6y=11\end{matrix}\kern 15pt消元后\kern 15pt\begin{matrix}x-2y=1\\\kern 18pt0y=8\end{matrix} x−2y=13x−6y=11消元后x−2y=10y=8 0 y = 8 0y=8 0y=8 无解。正常情况下是右侧的 8 8 8 除以第二个主元,但是这里没有第二个主元(零不允许是主元)。从 Figure 2.6 中的行图像和列图像可以看出失效的原因。如果系统无解,那么消元过程中就会出现类似 0 y = 8 0y=8 0y=8 这样形式的方程。

行图像中可以发现这是两条平行线,平行线是没有交点的,若方程组有解,那么这个解必定会同时落在两条直线上。这两条直线没有交点,所以方程组无解。
列图像中可以看出两个列向量 ( 1 , 3 ) (1,3) (1,3) 和 ( − 2 , − 6 ) (-2,-6) (−2,−6) 位于同一个方向(同向或反向),所有列的线性组合都在同一直线上,但是右侧的列 ( 1 , 11 ) (1,11) (1,11) 不在这条直线上。不存在正确列的线性组合可以得到右侧的向量,因此方程组无解。
若将右侧改为 ( 1 , 3 ) (1,3) (1,3),那么会因为一整条直线都是解而失效。例 2 是由无穷多个解。
【例2】无限多解而失效。将 b \boldsymbol b b 从 ( 1 , 11 ) (1,11) (1,11) 改成 ( 1 , 3 ) (1,3) (1,3)。 x − 2 y = 1 3 x − 6 y = 3 消元后 x − 2 y = 1 0 y = 0 仍然仅有一个主元 \begin{matrix}x-2y=1\\3x-6y=3\kern 4pt\end{matrix}\kern 15pt消元后\kern 15pt\begin{matrix}x-2y=1\\\kern 19pt0y=0\end{matrix}\kern 10pt仍然仅有一个主元 x−2y=13x−6y=3消元后x−2y=10y=0仍然仅有一个主元所有的 y y y 都满足方程 0 y = 0 0y=0 0y=0,实际上只有一个方程 x − 2 y = 1 x-2y=1 x−2y=1。未知数 y y y 是自由的,当 y y y 选定后,通过 x = 2 y + 1 x=2y+1 x=2y+1 也就可以确定 x x x。
Figure 2.7 是该方程组的行图像和列图像。

此时的行图像,两条平行线变成了同一条直线,直线上的每一点都同时满足两个方程。
列图像中, b = ( 1 , 3 ) \boldsymbol b=(1,3) b=(1,3) 与列 1 1 1 相同。所以列的线性组合可以是 x = 1 , y = 0 x=1,y=0 x=1,y=0,也可以是 x = 0 , y = − 1 / 2 x=0,y=-1/2 x=0,y=−1/2。对于每一行的解 ( x , y ) (x,y) (x,y) 同样也是列的解。
关于消元法:
失效 n \kern 10ptn n 个方程无法得到 n n n 个主元
消元法得到方程 0 ≠ 0 0\neq0 0=0(无解),或 0 = 0 0=0 0=0(无限多解)
得到 n n n 个主元表示成功,但是可能需要交换这 n n n 个方程的顺序。
第三种消元法失效的情况下可以通过交换方程的顺序来解决。假设第一个主元的位置是 0 0 0,而 0 0 0 不能作为主元。当第一个方程没有 x x x 项时,我们可以将它与下面的方程交换:
【例3】暂时失效(主元出现 0 0 0)。交换行可以得到两个主元: 重新排列 0 x + 2 y = 4 3 x − 2 y = 5 两个方程交换 3 x − 2 y = 5 2 y = 4 重新排列\kern 15pt\begin{matrix}0x+2y=4\\3x-2y=5\end{matrix}\kern 10pt两个方程交换\kern 15pt\begin{matrix}3x-2y=5\\\kern 24pt2y=4\end{matrix} 重新排列0x+2y=43x−2y=5两个方程交换3x−2y=52y=4新的系统已经是三角形了。这个例子可以直接进行回代,最后一个方程得到 y = 2 y=2 y=2,回代到第一个方程可以得到 x = 3 x=3 x=3。本例行图像是正常的(两条相交直线),列图像也是正常的(列向量不在同一方向)。主元 3 3 3 和 2 2 2 也是正常的。但是需要进行一次行交换。
例 1 和例 2 是奇异的 —— 没有第二个主元。例 3 是非奇异的 —— 每个主元都存在,仅有一个解。奇异方程无解或有无限多解,非奇异方程仅有一个解。主元因为要做除数,所以不能是零。
三、三个方程三个未知数
为了更深入的理解高斯消元法, 2 × 2 2×2 2×2 的系统是不够的,下面将以 3 × 3 3×3 3×3 的系统为例。现在的系数矩阵都是方形的 —— 行数与列数相等。 2 x + 4 y − 2 z = 2 4 x + 9 y − 3 z = 8 − 2 x − 3 y + 7 z = 10 ( 2.2.1 ) \begin{matrix}2x+4y-2z=2\\4x+9y-3z=8\\-2x-3y+7z=10\end{matrix}\kern 25pt(2.2.1) 2x+4y−2z=24x+9y−3z=8−2x−3y+7z=10(2.2.1)第一个主元是 2 2 2(左上角),这个主元下方是要消去的 4 4 4,第一个乘数就是 4 / 2 = 2 4/2=2 4/2=2。第一个方程乘 l 21 = 2 l_{21}=2 l21=2 后,用第二个方程减去上面的结果,即可将 4 x 4x 4x 消去:
步骤1: 从方程 2 中减去 2 乘方程 1,得: y + z = 4 y+z=4 y+z=4
我们也需要使用第一个主元消去第三个方程中的 − 2 x -2x −2x。最快的方法是将方程 3 与方程 1 相加,但是为了更系统的实现消元,我们仍然使用相同的方法,使用先乘后减的方法。乘数 l 31 = − 2 / 2 = − 1 l_{31}=-2/2=-1 l31=−2/2=−1,将其与第一个方程相乘后,在从第三个方程减去上述结果:
步骤2: 方程 3 减去 − 1 -1 −1 乘方程 1,得: y + 5 z = 12 y+5z=12 y+5z=12。
新的方程只包含了两个未知数 y y y 和 z z z,第二个主元是 1 1 1: x 已经被消去 1 y + 1 z = 4 1 y + 5 z = 12 x\,已经被消去\kern 10pt\begin{matrix}1y+1z=4\kern 6pt\\1y+5z=12\end{matrix} x已经被消去1y+1z=41y+5z=12我们已经得到一个 2 × 2 2×2 2×2 的系统,最后一步消去 y y y 得到 1 × 1 1×1 1×1 的系统:
步骤3: 新的方程 3 减去 1 1 1 乘新的方程 2,乘数是 l 32 = 1 / 1 = 1 l_{32}=1/1=1 l32=1/1=1,得到 4 z = 8 4z=8 4z=8。
原始的 A x = b A\boldsymbol x=\boldsymbol b Ax=b 转换成了上三角形 U x = c U\boldsymbol x=\boldsymbol c Ux=c:

至此消元的目的达成,从 A A A 到 U U U 完成了前向消元。注意 U U U 的对角线就是主元 2 , 1 , 4 2,1,4 2,1,4。原始系统中主元 1 1 1 和 4 4 4 被隐藏了,通过消元法可以找到它们。 U x = c U\boldsymbol x=\boldsymbol c Ux=c 的形式可以使用回代来解方程组了: ( 4 z = 8 得 z = 2 ) ( y + z = 4 得 y = 2 ) ( 2 x + 4 y − 2 z = 2 得 x = − 1 ) (4z=8\,得\,z=2)\kern 10pt(y+z=4\,得\,y=2)\kern 10pt(2x+4y-2z=2\,得\,x=-1) (4z=8得z=2)(y+z=4得y=2)(2x+4y−2z=2得x=−1)方程组的解是 ( x , y , z ) = ( − 1 , 2 , 2 ) (x,y,z)=(-1,2,2) (x,y,z)=(−1,2,2)。行图像中三个方程形成三个平面,这三个平面都会经过解。原始的平面都是倾斜的,经过消元后最后一个平面 4 z = 8 4z=8 4z=8 是水平的。
列图像显示列向量的线性组合 A x A\boldsymbol x Ax 产生右侧的向量 b \boldsymbol b b,组合系数 ( x , y , z ) = ( − 1 , 2 , 2 ) (x,y,z)=(-1,2,2) (x,y,z)=(−1,2,2): A x = ( − 1 ) [ 2 4 − 2 ] + 2 [ 4 9 − 3 ] + 2 [ − 2 − 3 7 ] = [ 2 8 10 ] = b ( 2.2.3 ) A\boldsymbol x=(-1)\begin{bmatrix}\kern 7pt2\\\kern 7pt4\\-2\end{bmatrix}+2\begin{bmatrix}\kern 7pt4\\\kern 7pt9\\-3\end{bmatrix}+2\begin{bmatrix}-2\\-3\\\kern 7pt7\end{bmatrix}=\begin{bmatrix}2\\8\\10\end{bmatrix}=\boldsymbol b\kern 10pt(2.2.3) Ax=(−1) 24−2 +2 49−3 +2 −2−37 = 2810 =b(2.2.3)三角形 U x = c U\boldsymbol x=\boldsymbol c Ux=c 与 A x = b A\boldsymbol x=\boldsymbol b Ax=b 有相同的列向量组合 ( − 1 , 2 , 2 ) (-1,2,2) (−1,2,2) 产生右侧向量。
四、从 A 到 U 的消元法
对于 4 × 4 4×4 4×4 或者 n × n n\times n n×n 的问题,消元法的步骤都是一样的。当高斯消元法成功时,系数矩阵将一列接一列的从 A A A 变成 U U U。
列1. \,\, 利用第一个方程将第一个主元下的都变成 0.
列2. \,\, 利用新得到的第二个方程将第二个主元下的都变成 0.
列 3 到列 n. \,\, 重复上述步骤,找到 n n n 个主元和上三角矩阵 U U U.
列 2 之后有 [ x x x x 0 x x x 0 0 x x 0 0 x x ] ,最终目标 [ x x x x 0 x x x 0 0 x x 0 0 0 x ] ( 2.1.4 ) 列\,2\,之后有\kern 8pt\begin{bmatrix}x&x&x&x\\0&x&x&x\\0&0&x&x\\0&0&x&x\end{bmatrix},最终目标\kern 8pt\begin{bmatrix}x&x&x&x\\0&x&x&x\\0&0&x&x\\0&0&0&x\end{bmatrix}\kern 10pt(2.1.4) 列2之后有 x000xx00xxxxxxxx ,最终目标 x000xx00xxx0xxxx (2.1.4)前向消元法的结果是一个上三角形系统,如果 n n n 个主元均存在(非零数字),则矩阵是非奇异的。
五、主要内容总结
- 线性系统 A x = b A\boldsymbol x=\boldsymbol b Ax=b 成功消元后变成上三角形 U x = c U\boldsymbol x=\boldsymbol c Ux=c。
- 从方程 i i i 减去 l i j l_{ij} lij 乘方程 j j j 使得单元 ( i , j ) (i,j) (i,j) 为 0 0 0。
- 乘数 l i j = 行 i 要消去的单元 行 j 的主元 l_{ij}=\displaystyle\frac{行\,i\,要消去的单元}{行 \,j\,的主元} lij=行j的主元行i要消去的单元,主元不为 0 0 0。
- 当主元的位置为 0 0 0 时,如果下面有非零单元,交换行。
- 上三角 U x = c U\boldsymbol x=\boldsymbol c Ux=c 使用回代的方法求解。(从底到上)
- 当消元法完全失效时, A x = b A\boldsymbol x=\boldsymbol b Ax=b 无解或有无限多解。
六、例题
【例4】对矩阵 A A A 进行消元法,第一主元和第二主元是什么?第一步的乘数 l 21 l_{21} l21 是什么(行 2 减去 l 21 l_{21} l21 乘行 1)? A = [ 1 1 0 1 2 1 0 1 2 ] → [ 1 1 0 0 1 1 0 1 2 ] → [ 1 1 0 0 1 1 0 1 1 ] = U A=\begin{bmatrix}1&1&0\\1&2&1\\0&1&2\end{bmatrix}\rightarrow\begin{bmatrix}1&1&0\\0&1&1\\0&1&2\end{bmatrix}\rightarrow\begin{bmatrix}1&1&0\\0&1&1\\0&1&1\end{bmatrix}=U A= 110121012 → 100111012 → 100111011 =U矩阵 A A A 的 ( 2 , 2 ) (2,2) (2,2) 位置上数字变为多少会使得行 2 2 2 和行 3 3 3 必须交换?
为什么左下角的乘数 l 31 = 0 l_{31}=0 l31=0,需要行 3 3 3 减去 0 0 0 乘行 1 1 1?
如果将角落的单元 a 33 = 2 a_{33}=2 a33=2 改成 a 33 = 1 a_{33}=1 a33=1,为什么会使得消元法失败?
解: 第一主元是 1 1 1,第二主元也是 1 1 1,乘数 l 21 = 1 / 1 = 1 l_{21}=1/1=1 l21=1/1=1。
若将矩阵 A A A 的 ( 2 , 2 ) (2,2) (2,2) 位置的单元改成 1 1 1,那么就必须要交换行 2 2 2 和行 3 3 3。
因为 a 31 = 0 a_{31}=0 a31=0,所以 l 31 = 0 / 1 = 0 l_{31}=0/1=0 l31=0/1=0。某一行的开始是 0 0 0 则不需要消元。矩阵 A A A 是一个带状矩阵,中心带之外的都为 0 0 0。
如果原始角落的单元 a 33 a_{33} a33 改成 1 1 1,消元法就会产生 0 0 0。没有第三个主元,消元法失败。
【例5】假设 A A A 是一个三角形矩阵(上三角或下三角),主元会在什么位置?对于任意的 b \boldsymbol b b,什么情况下 A x = b A\boldsymbol x=\boldsymbol b Ax=b 有且仅有一个确切的解?
解: 矩阵的对角线就是主元的位置。
当这些主元全都不是 0 0 0 时,消元法执行成功可以。若 A A A 是上三角,使用回代;若 A A A 是下三角,使用前向代入。
【例6】使用消元法得到上三角形矩阵 U U U。通过回代求解,或者解释为什么无法执行?主元(不为 0 0 0)是什么?必要时可以交换方程的顺序。下面两个系统的唯一区别是最后一个方程的 − x -x −x。 成功 x + y + z = 7 x + y − z = 5 x − y + z = 3 失败 x + y + z = 7 x + y − z = 5 − x − y + z = 3 成功\kern 10pt\begin{matrix}x+y+z=7\\x+y-z=5\\x-y+z=3\end{matrix}\kern 15pt失败\kern 10pt\begin{matrix}x+y+z=7\\x+y-z=5\\-x-y+z=3\kern 6pt\end{matrix} 成功x+y+z=7x+y−z=5x−y+z=3失败x+y+z=7x+y−z=5−x−y+z=3解: 对于系统 1,方程 2 和方程 3 分别减去方程 1(乘数 l 21 = 1 , l 31 = 1 l_{21}=1,l_{31}=1 l21=1,l31=1),由于 ( 2 , 2 ) (2,2) (2,2) 的位置会变成 0,所以交换方程 2 和 3 的顺序: 成功 x + y + z = 7 0 y − 2 z = − 2 − 2 y + 0 z = − 4 交换行后 x + y + z = 7 − 2 y + 0 z = − 4 − 2 z = − 2 成功\kern 10pt\begin{matrix}x+y+z=7\\\kern 16pt0y-2z=-2\\\kern 10pt-2y+0z=-4\end{matrix}\kern 15pt交换行后\kern 10pt\begin{matrix}x+y+z=7\\\kern 9pt-2y+0z=-4\\\kern 33pt-2z=-2\end{matrix} 成功x+y+z=70y−2z=−2−2y+0z=−4交换行后x+y+z=7−2y+0z=−4−2z=−2回代后可得 z = 1 , y = 2 , x = 4 z=1,y=2,x=4 z=1,y=2,x=4。主元是 1 , − 2 , − 2 1,-2,-2 1,−2,−2。
对于系统 2,执行消元后: 失败 x + y + z = 7 0 y − 2 z = − 2 0 y + 2 z = 10 列 2 没有主元 ( 它就是列 1 ) 进一步消元得到 0 z = 8 三个平面 不相交 于一点 失败\kern 10pt\begin{matrix}x+y+z=7\\\kern16pt0y-2z=-2\\\kern 16pt0y+2z=10\end{matrix}\kern 15pt\begin{matrix}列\,2\,\pmb{没有主元}(它就是列\,1)\\进一步消元得到\,0z=8\kern 12pt\\三个平面\pmb{不相交}于一点\kern 11pt\end{matrix} 失败x+y+z=70y−2z=−20y+2z=10列2没有主元(它就是列1)进一步消元得到0z=8三个平面不相交于一点平面 1 与平面 2 相交于一条直线,平面 2 与 平面 3 平行,该方程组无解。
如果将第三个方程中的 3 3 3 改成 − 5 -5 −5,则消元法会得到 0 = 0 0=0 0=0,有无限多个解。三个平面相交于一条直线。此时第三个平面和第二个平面重合。
相关文章:

2.2 消元法的概念
一、消元法介绍 消元法(elimination)是一个求解线性方程组的系统性方法。下面是使用消元法求解一个 2 2 2\times2 22 线性方程组的例子。消元之前,两个方程都有 x x x 和 y y y,消元后,第一个未知数 x x x 将从第…...

删除有序数组中的重复项
目录 题目: 示例: 题目分析: 解题思路: 题目: 给你一个 非严格递增排列 的数组 nums ,请你 原地 删除重复出现的元素,使每个元素 只出现一次 ,返回删除后数组的新长度。元素的…...
【数据库】
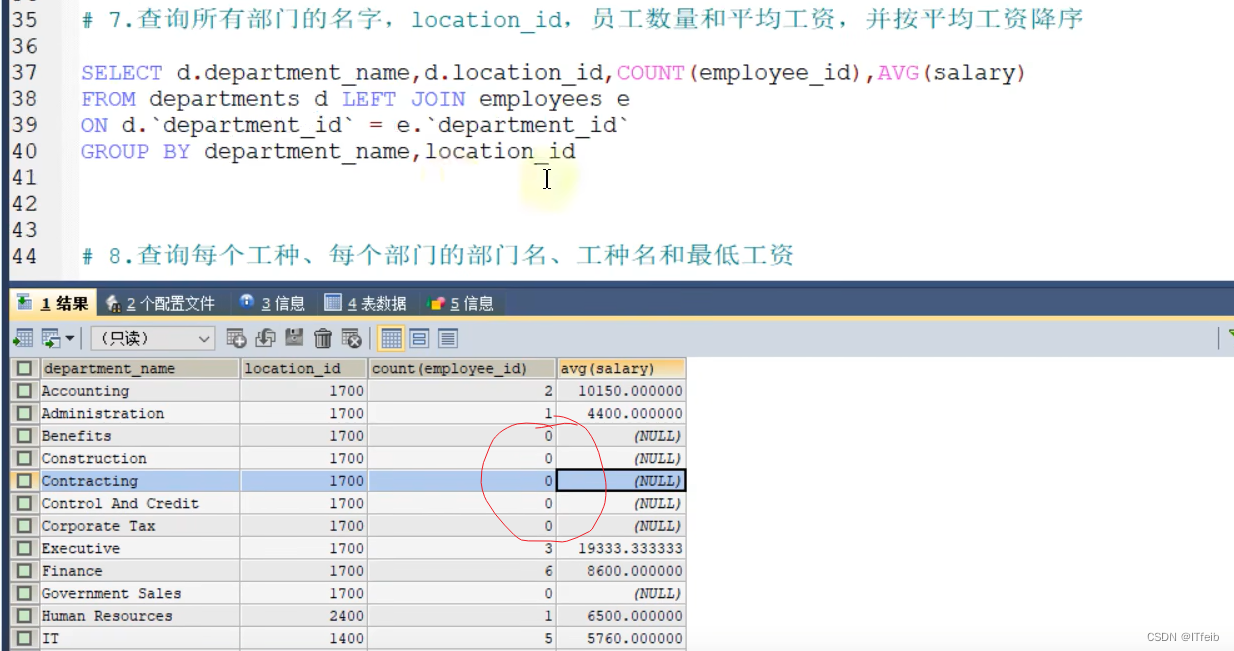
文章目录 1. 聚合函数练习: 2. 子查询 1. 聚合函数 where中过滤条件中不能写聚合函数,有聚合函数需要写到Having中 方式一效率高: Select执行流程 练习: 2. 第七题:count(*)有问题,原因是左外连接后…...

高级深入--day38
阳光热线问政平台 http://wz.sun0769.com/index.php/question/questionType?type4 爬取投诉帖子的编号、帖子的url、帖子的标题,和帖子里的内容。 items.py import scrapyclass DongguanItem(scrapy.Item):# 每个帖子的标题title scrapy.Field()# 每个帖子的编…...
基于springboot,vue校园社团管理系统
开发工具:IDEA 服务器:Tomcat9.0, jdk1.8 项目构建:maven 数据库:mysql5.7 系统分前后台,项目采用前后端分离 前端技术:vueelementUI 服务端技术:springbootmybatis-plus 本系…...

广州华锐互动:VR虚拟现实物理学习平台,开启数字化教学新格局
随着虚拟现实(VR)技术的不断发展,越来越多的领域开始应用这一技术。广州华锐互动开发的VR虚拟现实物理学习平台就得到了广泛应用,平台涉及力学、光学、热学等初中物理知识,还包含了物理名人、实验器具、物理现象的还原和学习,相比…...

【tio-websocket】8、T-IO对半包和粘包的处理
介绍 t-io对数据的解码是在DecodeRunnable中完成的,一个TCP连接对应一个DecodeRunnable半包粘包的处理也都在DecodeRunnable中完成的关于DecodeRunnable 先贴上 DecodeRunnable 的源代码: import java.nio.BufferUnderflowException; import java.nio.ByteBuffer; import j…...

【Linux】安装与配置虚拟机及虚拟机服务器坏境配置与连接
目录 操作系统介绍 什么是操作系统 常见操作系统 UNIX操作系统 linux操作系统 mac操作系统 嵌入式操作系统 个人版本和服务器版本的区别 安装VMWare虚拟机 VMWare虚拟网卡 编辑 配置虚拟网络编辑器 编辑 安装配置Windows Server 2012 R2 安装Windows Server 2…...

Redis常识
文章目录 缓存的三个风险数据结构淘汰策略 和 过期删除策略过期删除淘汰 如何理解单线程redis特性复制gossip协议事务(和mysql不同,是不严格的事务 )集群(高可用)管道持久化 缓存的三个风险 缓存雪崩(缓存…...

Instant,LocalDate,LocalTime,LocalDateTime和ZonedDateTime
Instant 封装了从 1970-01-01T00:00:00Z 开始的秒数,相当于时间戳。 主要有两个属性: private final long seconds; private final int nanos;LocalDate 用于表示日期,包括年、月、日,例如 2017-12-03。 主要有三个属性&…...

Web入门笔记
Web入门笔记 HTTP协议 超文本传输协议 规定了浏览器和服务器之间数据传输的规则,请问数据和响应数据的格式 基于TCP请求-响应模式一次请求对应一次响应无状态的协议 请问数据格式 浏览器版本:解决浏览器兼容问题。GET请求体:存放请求参数…...

Linux网络编程二(TCP三次握手、四次挥手、TCP滑动窗口、MSS、TCP状态转换、多进程/多线程服务器实现)
TCP三次握手 TCP三次握手(TCP three-way handshake)是TCP协议建立可靠连接的过程,确保客户端和服务器之间可以进行可靠的通信。下面是TCP三次握手的详细过程: 假设客户端为A,服务器为B 1、第一次握手(SYN1,seq500&…...
C#和.NET Framework)
C#核心笔记——(一)C#和.NET Framework
C#是一种通用的,类型安全的面向对象编程语言。其目标是提高程序员生产力。 一.面向对象 C#实现了丰富的面向对象范式,包括封装、继承、多态。 C#面向对象特性包括: 统一的类型系统 类与接口 属性、方法、事件 C#支持纯函数模式 二、类型安…...

【2023年冬季】华为OD统一考试(B卷)题库清单(已收录345题),又快又全的 B 卷题库大整理
目录 专栏导读华为OD机试算法题太多了,知识点繁杂,如何刷题更有效率呢? 一、逻辑分析二、数据结构1、线性表① 数组② 双指针 2、map与list3、队列4、滑动窗口5、二叉树6、并查集7、栈 三、算法1、基础算法① 贪心算法② 二分查找③ 分治递归…...

云服务器的先驱,亚马逊云科技海外云服务器领军者
随着第三次工业革命的发展,移动互联网技术带来的信息技术革命为我们的生活带来了极大的便捷。其中,不少优秀的云服务器产品发挥了不可低估的作用,你或许听说过亚马逊云科技、谷歌GCP、IBM Cloud等优秀的海外云服务器。那么云服务器有哪些&…...
QT webengine显示HTML简单示例
文章目录 参考示例1TestWebenqine.promainwindow.hmainwindow.cppmain.cpp效果 示例2 (使用setDevToolsPage函数)main.cpp效果 参考 QT webengine显示HTML简单示例 示例1 编译器 : Desktop Qt 5.15.2 MSVC2019 64bit编辑器: QtCreator代码: TestWebenqine.pro # TestWeben…...
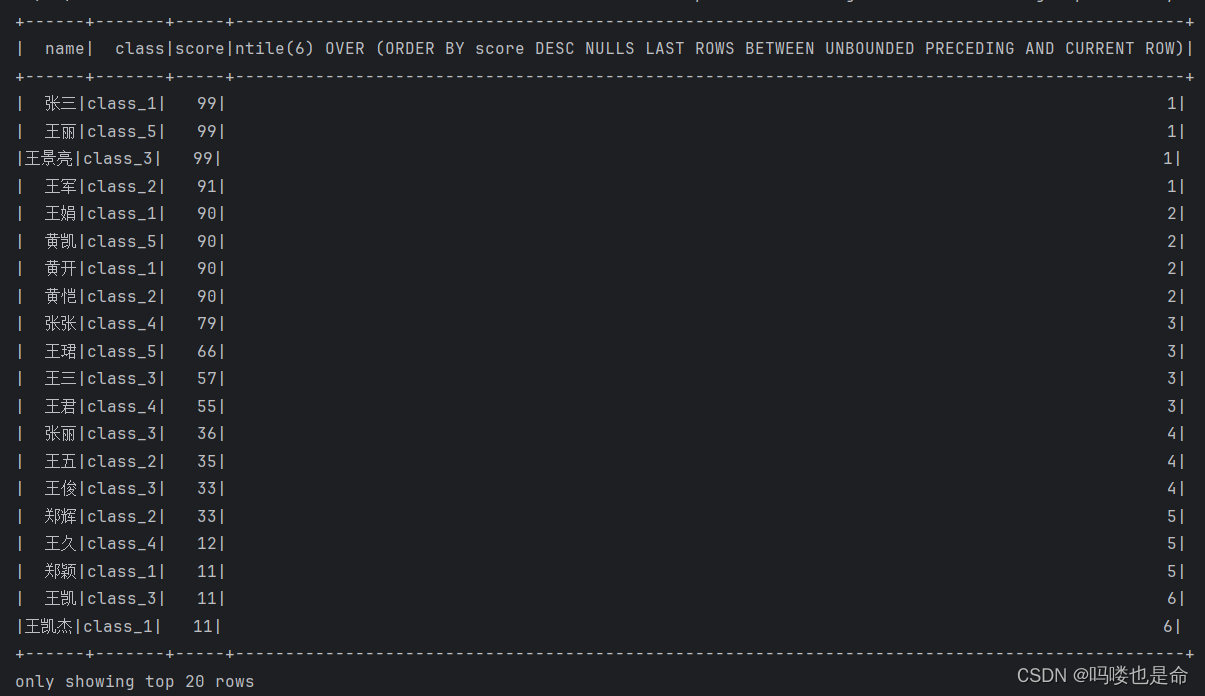
Spark_SQL函数定义(定义UDF函数、使用窗口函数)
一、UDF函数定义 (1)函数定义 (2)Spark支持定义函数 (3)定义UDF函数 (4)定义返回Array类型的UDF (5)定义返回字典类型的UDF 二、窗口函数 (1&…...

【Leetcode】【每日一题】【中等】274. H 指数
力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台备战技术面试?力扣提供海量技术面试资源,帮助你高效提升编程技能,轻松拿下世界 IT 名企 Dream Offer。https://leetcode.cn/problems/h-index/description/?envTyped…...

MySQL读写分离技术及实现方案
MySQL读写分离技术及实现方案 本文主要介绍了MySQL读写分离技术的原理、实现方案以及示例。通过使用读写分离技术,可以提高数据库的性能,降低服务器的压力。 一、MySQL读写分离技术简介 读写分离是指将数据库的读操作和写操作分别分配到不同的服务器上…...
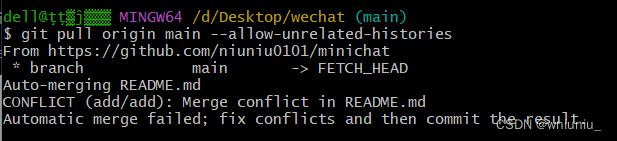
git 推送到github远程仓库细节处理(全网最良心)
我查看了很多网上的教程都不是很好 我们先在github创建一个仓库,且初始化 readme 我们到本地文件初始化仓库 添加远程仓库 这时候我们就 git add . , git commit ,再准备git push 的时候 显示没有指定远程的分支 我们按照提示操作 提示我们要先git pull 提示我…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

nnUNet V2修改网络——暴力替换网络为UNet++
更换前,要用nnUNet V2跑通所用数据集,证明nnUNet V2、数据集、运行环境等没有问题 阅读nnU-Net V2 的 U-Net结构,初步了解要修改的网络,知己知彼,修改起来才能游刃有余。 U-Net存在两个局限,一是网络的最佳深度因应用场景而异,这取决于任务的难度和可用于训练的标注数…...
