pytorch 笔记:KLDivLoss
1 介绍
对于具有相同形状的张量 ypred 和 ytrue(ypred 是输入,ytrue 是目标),定义逐点KL散度为:
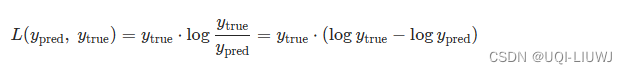
为了在计算时避免下溢问题,此KLDivLoss期望输入在对数空间中。如果log_target=True,则目标也在对数空间。

2 参数
| reduction |
reduction= “mean”不返回真正的KL散度值,reduction= “batchmean”才是 |
| log_target | 指定目标是否在对数空间中 |
3 举例
import torch
import torch.nn as nninput = torch.tensor([[0.5, -0.5, 0.1], [0.1, -0.2, 0.3]], requires_grad=True)target = torch.tensor([[0.7, 0.2, 0.1], [0.1, 0.5, 0.4]])loss_function = nn.KLDivLoss(reduction='batchmean')
loss = loss_function(input, target)
print(loss)
#tensor(-1.0176, grad_fn=<DivBackward0>)等价手动形式:
target*(target.log()-input)
'''
tensor([[-0.5997, -0.2219, -0.2403],[-0.2403, -0.2466, -0.4865]], grad_fn=<MulBackward0>)
'''#这里的每个元素计算方式为:
'''
tensor([[-0.5997, -0.2219, -0.2403],[-0.2403, -0.2466, -0.4865]], grad_fn=<MulBackward0>)
'''torch.sum(target*(target.log()-input))/2
#tensor(-1.0176, grad_fn=<DivBackward0>)相关文章:

pytorch 笔记:KLDivLoss
1 介绍 对于具有相同形状的张量 ypred 和 ytrue(ypred 是输入,ytrue 是目标),定义逐点KL散度为: 为了在计算时避免下溢问题,此KLDivLoss期望输入在对数空间中。如果log_targetTrue,则目标…...
父子项目打包发布至私仓库
父子项目打包发布至私仓库 1、方法一 在不需要发布至私仓的模块上添加如下代码: <plugin><groupId>org.apache.maven.plugins</groupId><artifactId>maven-deploy-plugin</artifactId><configuration><skip>true</s…...

汽车网络安全--ECU的安全更新
目前,汽车ECU的软件更新可以总结分成三大类: 工厂刷写模式:工厂大批量刷写或者升级,一般在出厂用; 工程模式:4S店、工厂等专业人员进行的ECU固件更新,通常是动力、转向、车控等; 车主模式:车主根据云端推送信息,通过IVI进行应用软件更新;目前也有趋势通过这种方式刷…...

NLP之搭建RNN神经网络
文章目录 代码展示代码意图代码解读知识点介绍1. Embedding2. SimpleRNN3. Dense 代码展示 # 构建RNN神经网络 from tensorflow.keras.models import Sequential from tensorflow.keras.layers import Dense, SimpleRNN, Embedding import tensorflow as tfrnn Sequential() …...

Android问题笔记四十三:JNI 开发如何快速定位崩溃问题
点击跳转>Unity3D特效百例点击跳转>案例项目实战源码点击跳转>游戏脚本-辅助自动化点击跳转>Android控件全解手册点击跳转>Scratch编程案例点击跳转>软考全系列 👉关于作者 专注于Android/Unity和各种游戏开发技巧,以及各种资源分享&…...
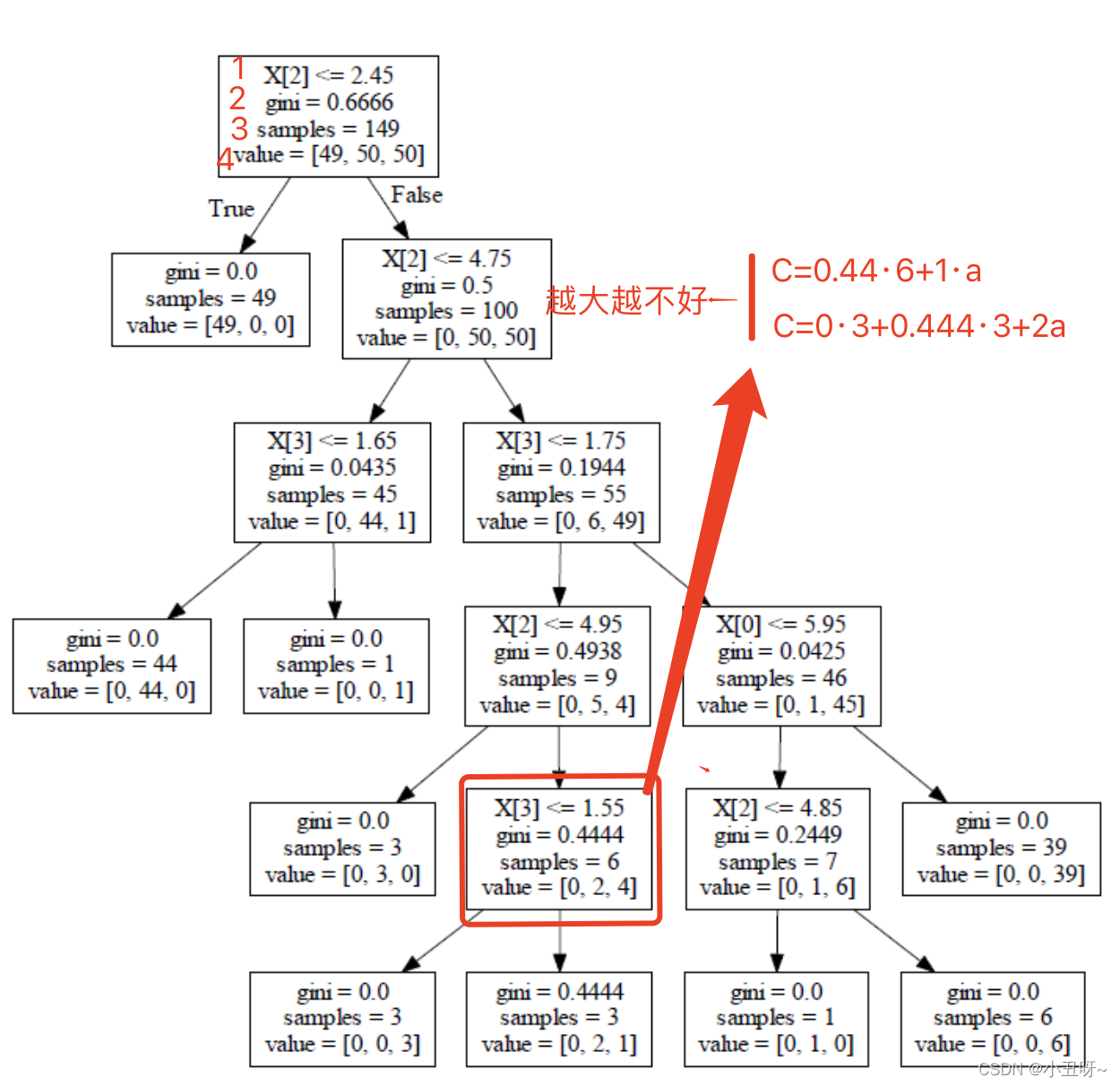
机器学习 | 决策树算法
一、决策树算法概述 1、树模型 决策树:从根节点开始一步步走到叶子节点(决策)。所有的数据最终都会落到叶子节点,既可以做分类也可以做回归。 在分类问题中,表示基于特征对实例进行分类的过程,可以认为是if-then的集合࿰…...

javascript中各种风骚的代码
1.判断数值符号是否相同 function numericSymbolsIsEqual(x: number, y: number): boolean {return (x ^ y) > 0}console.log(numericSymbolsIsEqual(1, 1))console.log(numericSymbolsIsEqual(-1, 1))console.log(numericSymbolsIsEqual(1, -1))console.log(numericSymbols…...

el-tree横向纵向滚动条
el-tree未展开时样式 el-tree展开时样式 给容器一个高度,然后样式加上overflow: scroll,这样纵向滚动条就出来了。 <el-card style"height: 528px;overflow: scroll"><el-inputplaceholder"输入关键字进行过滤"v-model&…...

STM32G030F6P6 芯片实验 (一)
STM32G030F6P6 芯片实验 (一) 淘宝搞了几片, 没试过 G系列, 试试感觉. 先搞片小系统版: 套 STM32F103C8T6小系统板格式. 原理图: (1) Ref 有点跳, 从 STM32F103C8T6 系统板改的, 没重编号. (2) Type-C 纯给电, 砍了 16pin的, 直接换 6pin的。 (3) 测试LED放 B2。 (4) 测试底…...
Wpf 使用 Prism 实战开发Day01
一.开发环境准备 1. VisualStudio 2022 2. .NET SDK 7.0 3. Prism 版本 8.1.97 以上环境,如有新的版本,可自行选择安装新的版本为主 二.创建Wpf项目 1.项目的名称:MyToDo 项目名称:这里只是记录学习,所以随便命名都无所谓,只要觉得合理就…...

6G关键新兴技术- 智能超表面(RIS)技术演进
摘要: 根据欧盟5G公私联盟协会定义,可重构智慧表面技术是由能够任意塑造电磁波面的材料组成,几乎是被动设备,可以适应或改变发射器和接收器之间的无线电信号。 一、产品定义及范围 根据欧盟5G公私联盟协会(5G Infrastructure P…...
【redhat9.2】搭建Discuz-X3.5网站
步骤 1.配置软件仓库 2.安装对应的软件 httpd php* mariadb* 3.启动服务 httpd mariadb 4.配置数据库 创建数据库 修改root密码 数据库的 5.传源码包(Discuz-X3.5) 解压 6.web页面初始化 关闭防火墙 允许http服务通过 修改权限 实…...

算法篇 : 并查集
介绍 英文名:union find set 作用:合并集合,查询集合 合并:将有直接关系的顶点放在一个集合里面 查找:查询某个顶点所属的集合 集合的标志:用祖先点的标号作为每个集合的标识 案例 如果说将下图的集合2合并…...

AM@微积分基本定理@微积分第二基本定理
文章目录 abstract微积分第二基本定理微积分基本公式公式书写例 结合不定积分的方法求定积分定积分换元法证明 定积分换元公式逆用例 和不定积分第二类换元法的差别定积分分部积分法例 abstract 微积分第一基本定理告诉我们,总是能够通过积分法构造(表达)一个连续函数的原函数…...

goland常用快捷键
移动光标 控制光标的移动:fn上下左右 移至当前页的页头:ctrlPgUp 移至并选中光标到当前页头:ctrlshiftPgUp 移至当前页的页尾:ctrlPgDn 移至并选中当前光标到当前页尾:ctrlshiftPgDn 返回到当前的光标处…...

CSDN写文章时常见问题及技巧
CSDN写文章时常见问题及技巧 1.有序待续、更新中 1.有序 过程: 写 1.空格 ,注意“.”后加个空格就可以生成序号,随心所欲编辑了 待续、更新中 ————————————————————— 以上就是今日博客的全部内容了 创作不易,若对您有…...
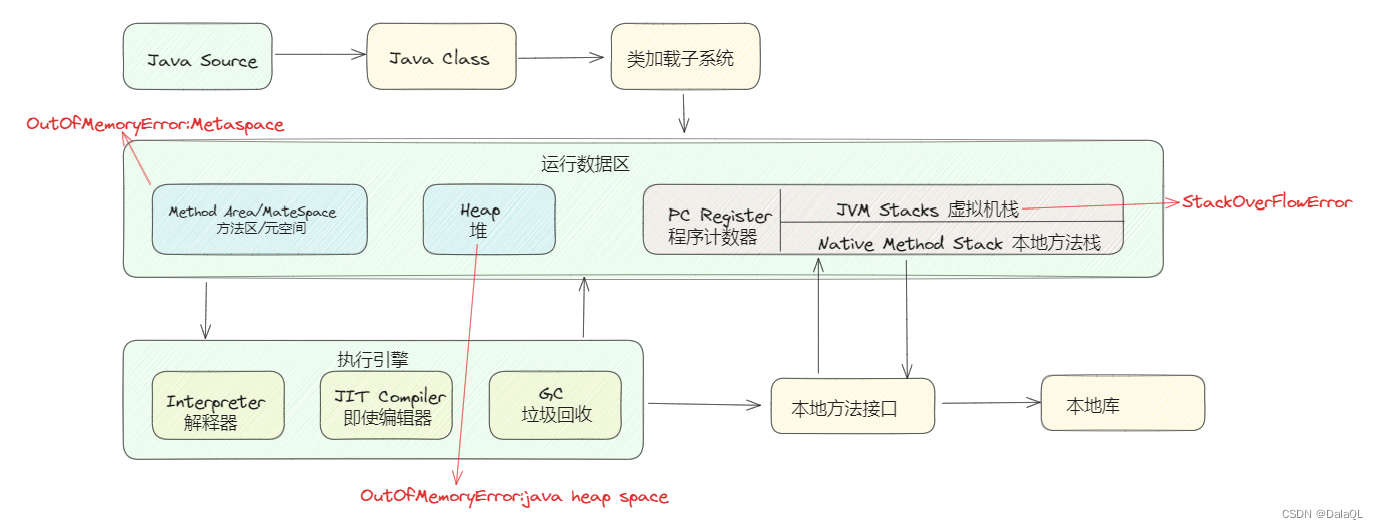
JVM虚拟机详解
目录 01JVM由哪些部分组成/运行流程 什么是程序计数器 详细介绍堆 介绍方法区(Method Area) 直接内存 虚拟机栈(Java Virtual machine Stacks) 垃圾回收是否涉及栈内存 栈内存分配越大越好吗 方法内的局部变量是否线程安全 什么情况下会导致栈…...

Go 怎么操作 OSS 阿里云对象存储
1 介绍 在项目开发中,我们经常会使用对象存储,比如 Amazon 的 S3,腾讯云的 COS,阿里云的 OSS 等。本文我们以阿里云 OSS 为例,介绍怎么使用 Go 操作对象存储。 阿里云 OSS 提供了 REST Api 和 OSS Go SDK࿰…...

vue3 Suspense组件
在 Vue 3 中,<Suspense> 组件用于处理异步组件加载时的等待状态和错误处理。它允许你在加载异步组件时显示一个自定义的加载指示器,以及在加载失败时显示错误信息。以下是一个详细的 <Suspense> 组件的使用示例: 首先࿰…...

NlogPrismWPF
文章目录 Nlog&Prism&WPF日志模块实现原理添加配置注入服务应用测试其他模块怎么调用? Nlog&Prism&WPF 日志模块 介绍了为WPF框架Prism注册Nlog日志服务的方法 实现原理 无论是在WPF或者ASP.NET Core当中, 都可以使用ServiceCollection来做到着…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...
提供了哪些便利?)
现有的 Redis 分布式锁库(如 Redisson)提供了哪些便利?
现有的 Redis 分布式锁库(如 Redisson)相比于开发者自己基于 Redis 命令(如 SETNX, EXPIRE, DEL)手动实现分布式锁,提供了巨大的便利性和健壮性。主要体现在以下几个方面: 原子性保证 (Atomicity)ÿ…...

基于Springboot+Vue的办公管理系统
角色: 管理员、员工 技术: 后端: SpringBoot, Vue2, MySQL, Mybatis-Plus 前端: Vue2, Element-UI, Axios, Echarts, Vue-Router 核心功能: 该办公管理系统是一个综合性的企业内部管理平台,旨在提升企业运营效率和员工管理水…...
)
【LeetCode】3309. 连接二进制表示可形成的最大数值(递归|回溯|位运算)
LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 题目描述解题思路Java代码 题目描述 题目链接:LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 给你一个长度为 3 的整数数组 nums。 现以某种顺序 连接…...

关于uniapp展示PDF的解决方案
在 UniApp 的 H5 环境中使用 pdf-vue3 组件可以实现完整的 PDF 预览功能。以下是详细实现步骤和注意事项: 一、安装依赖 安装 pdf-vue3 和 PDF.js 核心库: npm install pdf-vue3 pdfjs-dist二、基本使用示例 <template><view class"con…...

结构化文件管理实战:实现目录自动创建与归类
手动操作容易因疲劳或疏忽导致命名错误、路径混乱等问题,进而引发后续程序异常。使用工具进行标准化操作,能有效降低出错概率。 需要快速整理大量文件的技术用户而言,这款工具提供了一种轻便高效的解决方案。程序体积仅有 156KB,…...

表单设计器拖拽对象时添加属性
背景:因为项目需要。自写设计器。遇到的坑在此记录 使用的拖拽组件时vuedraggable。下面放上局部示例截图。 坑1。draggable标签在拖拽时可以获取到被拖拽的对象属性定义 要使用 :clone, 而不是clone。我想应该是因为draggable标签比较特。另外在使用**:clone时要将…...
