leetcode-二叉树
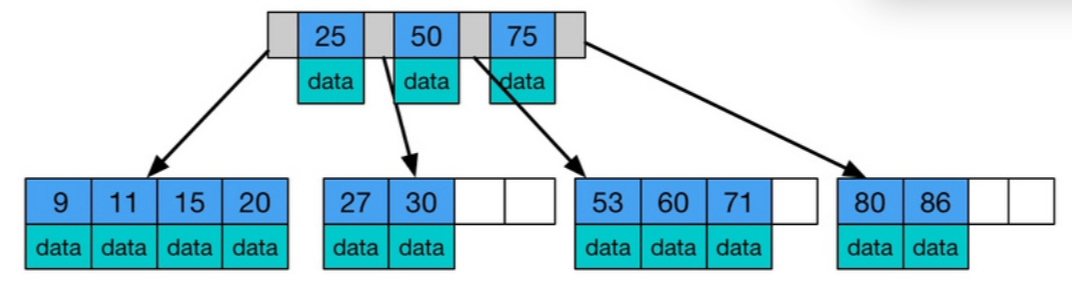
- B树和B+树的区别
- B树,也即balance树,是一棵多路自平衡的搜索树。它类似普通的平衡二叉树,不同的一点是B树允许每个节点有更多的子节点。
- B+树内节点不存储数据,所有关键字都存储在叶子节点上。
- B树:
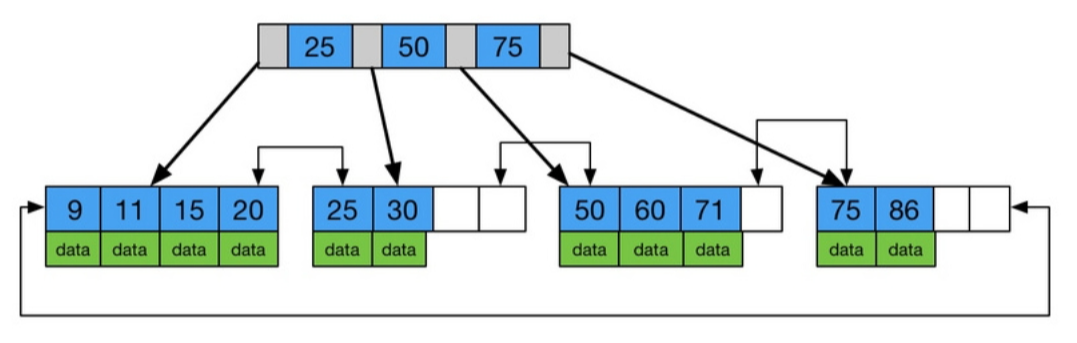
B+树:
二叉树理论基础:
1.种类:满二叉树、完全二叉树、二叉搜索树、平衡二叉树。
完全二叉树是最后一行从左到右连续但不一定全满。
二叉搜索树,必须有一定顺序。查询和添加都是O(logn),因为添加就是查询的过程。
平衡二叉搜索树:左右子树高度差的绝对值不超过1。map,set,multimap,multiset底层都是平衡二叉搜索树(是红黑树,红黑树是一种平衡二叉搜索树。)
2.存储方式:链表、数组。
链表,就是val,Treenode* left, Treenode *right
数组,一开始从0开始,左孩子就是2k+1,右孩子就是2k+2
3.遍历方式:
深度优先搜索:前序(中左右)、中序(左中右)、后序(左右中)。一般用递归实现,也可以迭代实现。
广度优先搜索:层序遍历是其中一种。
图的深度优先搜索就对应树的前中后序,图的广度优先搜索就对应树的层序遍历。
1. 二叉树的前,中,后序遍历 - 递归 leetcode144.94.145 20231026
代码随想录又卡了,栈与队列最后那题打着C++已实现的优先队列的旗号实际上是堆,而堆本身又是完全二叉树.....优先队列那题还不是直接拿的priority_queue去实现的,还自定义了它的比较规则,这又引出一个函数对象的概念,总之是无从下手,遂转战二叉树。今天看了看二叉树的理论知识,感觉还行,结果写题的时候又被递归摆了一道,完全忘了return和题干给的函数有什么用。
总之,题干给的preorderTraversal没动,自己重新实现了一个函数,调用之即可。下面两题是类似的。
class Solution { public:void preorder(TreeNode* cur, vector<int>& vct) {if(cur == nullptr){return;}vct.push_back(cur->val);preorder(cur->left,vct);preorder(cur->right,vct);}vector<int> preorderTraversal(TreeNode* root){vector<int> vct;preorder(root,vct);return vct;}};2. 二叉树的前,中,后序遍历 - 迭代leetcode144.94.145 20231027
迭代分为前后,中两种,理解起来其实还是很困难的,看代码貌似记住了,自己写对了,但是再过几天让我写是绝对写不出来的
前后之所以说是“一种”,因为后序可以由前序倒一下左右,再reverse一下数组就能得到。他们遍历和处理的顺序都是一样的,而中序就不一样了。
下面来看一下具体的代码~
前序,后序在这里就只放前序了:
class Solution { public:vector<int> preorderTraversal(TreeNode* root) {stack<TreeNode*> stk;vector<int> vct;if(root == nullptr)return vct;stk.push(root);while(!stk.empty()){TreeNode* cur = stk.top();stk.pop();vct.push_back(cur->val);if(cur->right !=nullptr)stk.push(cur->right);if(cur->left !=nullptr)stk.push(cur->left);}return vct;} };定义一个stk用于模拟递归,一个vct用户返回数组。因为要先push root进去,所以先得判断一下是否为空。
root被push进去以后,只要栈不为空,就pop栈顶出来,再把刚出的栈顶push到 vct 里面去,然后先往栈里push右边,再往栈里push左边。这样的话,之后vct就会从栈顶开始出,就会先被push_back到vct里面去,而后又是往复的右左栈入,中(栈里元素)左右vct出。
中序
class Solution { public:vector<int> inorderTraversal(TreeNode* root) {vector<int> vct;stack<TreeNode*> stk;TreeNode* cur = root;while(cur != nullptr || !stk.empty()){if(cur != nullptr){stk.push(cur);cur = cur->left;//入栈,然后cur一直到最左边}else{cur = stk.top();//已经为空了,就取栈头的成为现在的curstk.pop();vct.push_back(cur->val);cur = cur->right;}}return vct;} };未完待续
相关文章:

leetcode-二叉树
B树和B树的区别 B树,也即balance树,是一棵多路自平衡的搜索树。它类似普通的平衡二叉树,不同的一点是B树允许每个节点有更多的子节点。 B树内节点不存储数据,所有关键字都存储在叶子节点上。B树: B树: 二叉…...
【鸿蒙软件开发】ArkTS基础组件之TextTimer(文本显示计时)、TimePicker(时间选择)
文章目录 前言一、TextTimer1.1 子组件1.2 接口参数TextTimerController 1.3 属性1.4 事件1.5 示例代码 二、TimePicker2.1 子组件2.2 接口参数 2.3 属性2.4 事件TimePickerResult对象说明 2.5 示例代码 总结 前言 通过文本显示计时信息并控制其计时器状态的组件。 时间选择组…...

pytorch 笔记:KLDivLoss
1 介绍 对于具有相同形状的张量 ypred 和 ytrue(ypred 是输入,ytrue 是目标),定义逐点KL散度为: 为了在计算时避免下溢问题,此KLDivLoss期望输入在对数空间中。如果log_targetTrue,则目标…...
父子项目打包发布至私仓库
父子项目打包发布至私仓库 1、方法一 在不需要发布至私仓的模块上添加如下代码: <plugin><groupId>org.apache.maven.plugins</groupId><artifactId>maven-deploy-plugin</artifactId><configuration><skip>true</s…...

汽车网络安全--ECU的安全更新
目前,汽车ECU的软件更新可以总结分成三大类: 工厂刷写模式:工厂大批量刷写或者升级,一般在出厂用; 工程模式:4S店、工厂等专业人员进行的ECU固件更新,通常是动力、转向、车控等; 车主模式:车主根据云端推送信息,通过IVI进行应用软件更新;目前也有趋势通过这种方式刷…...

NLP之搭建RNN神经网络
文章目录 代码展示代码意图代码解读知识点介绍1. Embedding2. SimpleRNN3. Dense 代码展示 # 构建RNN神经网络 from tensorflow.keras.models import Sequential from tensorflow.keras.layers import Dense, SimpleRNN, Embedding import tensorflow as tfrnn Sequential() …...

Android问题笔记四十三:JNI 开发如何快速定位崩溃问题
点击跳转>Unity3D特效百例点击跳转>案例项目实战源码点击跳转>游戏脚本-辅助自动化点击跳转>Android控件全解手册点击跳转>Scratch编程案例点击跳转>软考全系列 👉关于作者 专注于Android/Unity和各种游戏开发技巧,以及各种资源分享&…...
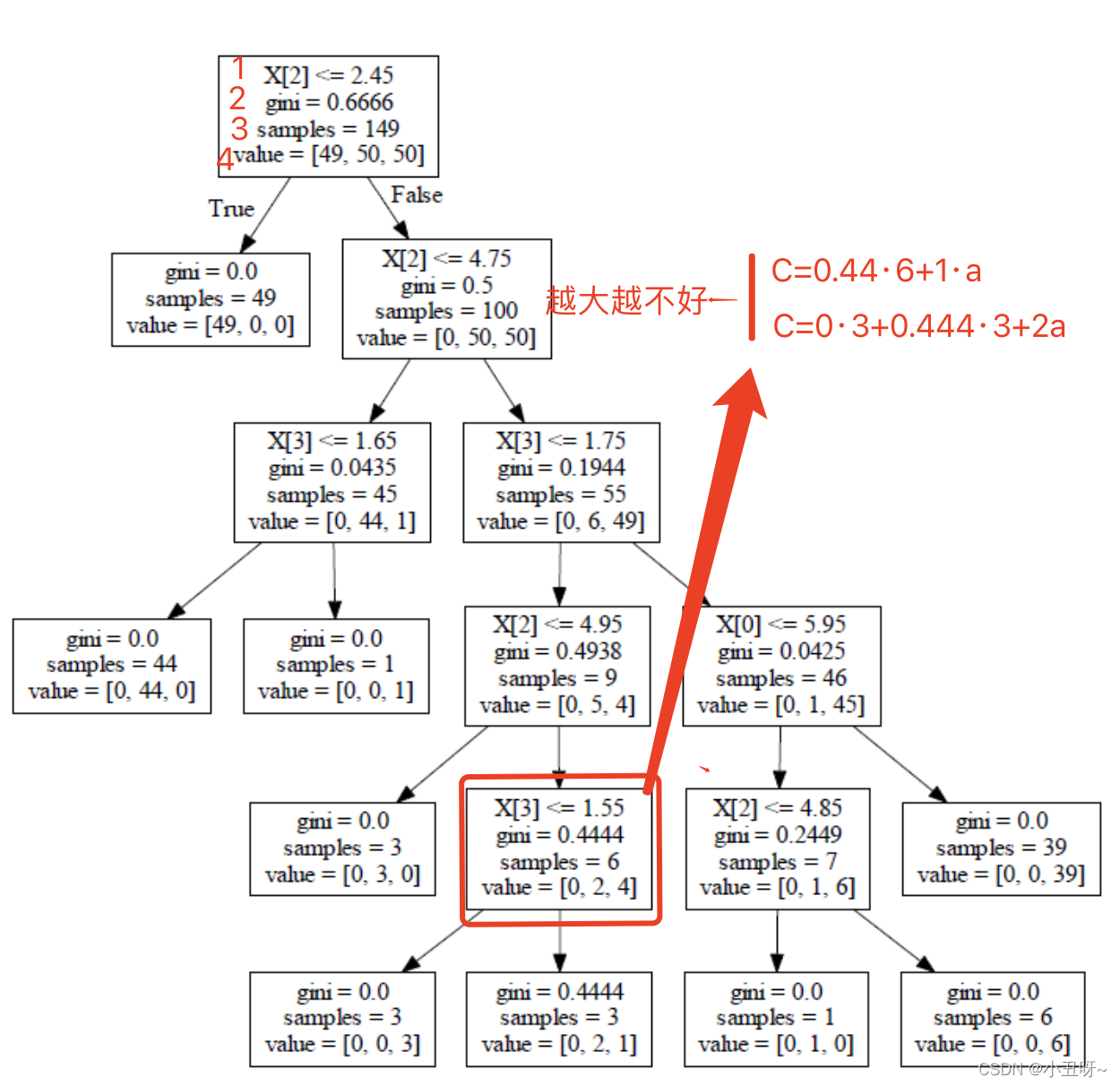
机器学习 | 决策树算法
一、决策树算法概述 1、树模型 决策树:从根节点开始一步步走到叶子节点(决策)。所有的数据最终都会落到叶子节点,既可以做分类也可以做回归。 在分类问题中,表示基于特征对实例进行分类的过程,可以认为是if-then的集合࿰…...

javascript中各种风骚的代码
1.判断数值符号是否相同 function numericSymbolsIsEqual(x: number, y: number): boolean {return (x ^ y) > 0}console.log(numericSymbolsIsEqual(1, 1))console.log(numericSymbolsIsEqual(-1, 1))console.log(numericSymbolsIsEqual(1, -1))console.log(numericSymbols…...

el-tree横向纵向滚动条
el-tree未展开时样式 el-tree展开时样式 给容器一个高度,然后样式加上overflow: scroll,这样纵向滚动条就出来了。 <el-card style"height: 528px;overflow: scroll"><el-inputplaceholder"输入关键字进行过滤"v-model&…...

STM32G030F6P6 芯片实验 (一)
STM32G030F6P6 芯片实验 (一) 淘宝搞了几片, 没试过 G系列, 试试感觉. 先搞片小系统版: 套 STM32F103C8T6小系统板格式. 原理图: (1) Ref 有点跳, 从 STM32F103C8T6 系统板改的, 没重编号. (2) Type-C 纯给电, 砍了 16pin的, 直接换 6pin的。 (3) 测试LED放 B2。 (4) 测试底…...
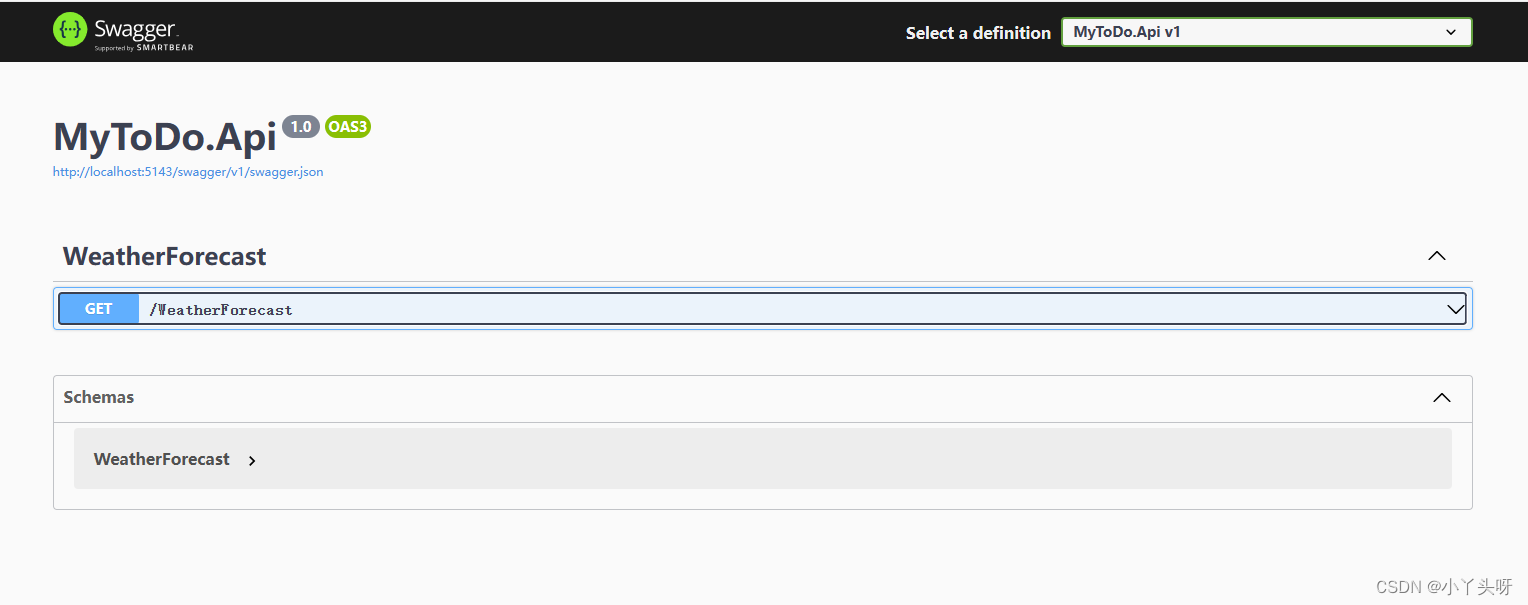
Wpf 使用 Prism 实战开发Day01
一.开发环境准备 1. VisualStudio 2022 2. .NET SDK 7.0 3. Prism 版本 8.1.97 以上环境,如有新的版本,可自行选择安装新的版本为主 二.创建Wpf项目 1.项目的名称:MyToDo 项目名称:这里只是记录学习,所以随便命名都无所谓,只要觉得合理就…...

6G关键新兴技术- 智能超表面(RIS)技术演进
摘要: 根据欧盟5G公私联盟协会定义,可重构智慧表面技术是由能够任意塑造电磁波面的材料组成,几乎是被动设备,可以适应或改变发射器和接收器之间的无线电信号。 一、产品定义及范围 根据欧盟5G公私联盟协会(5G Infrastructure P…...
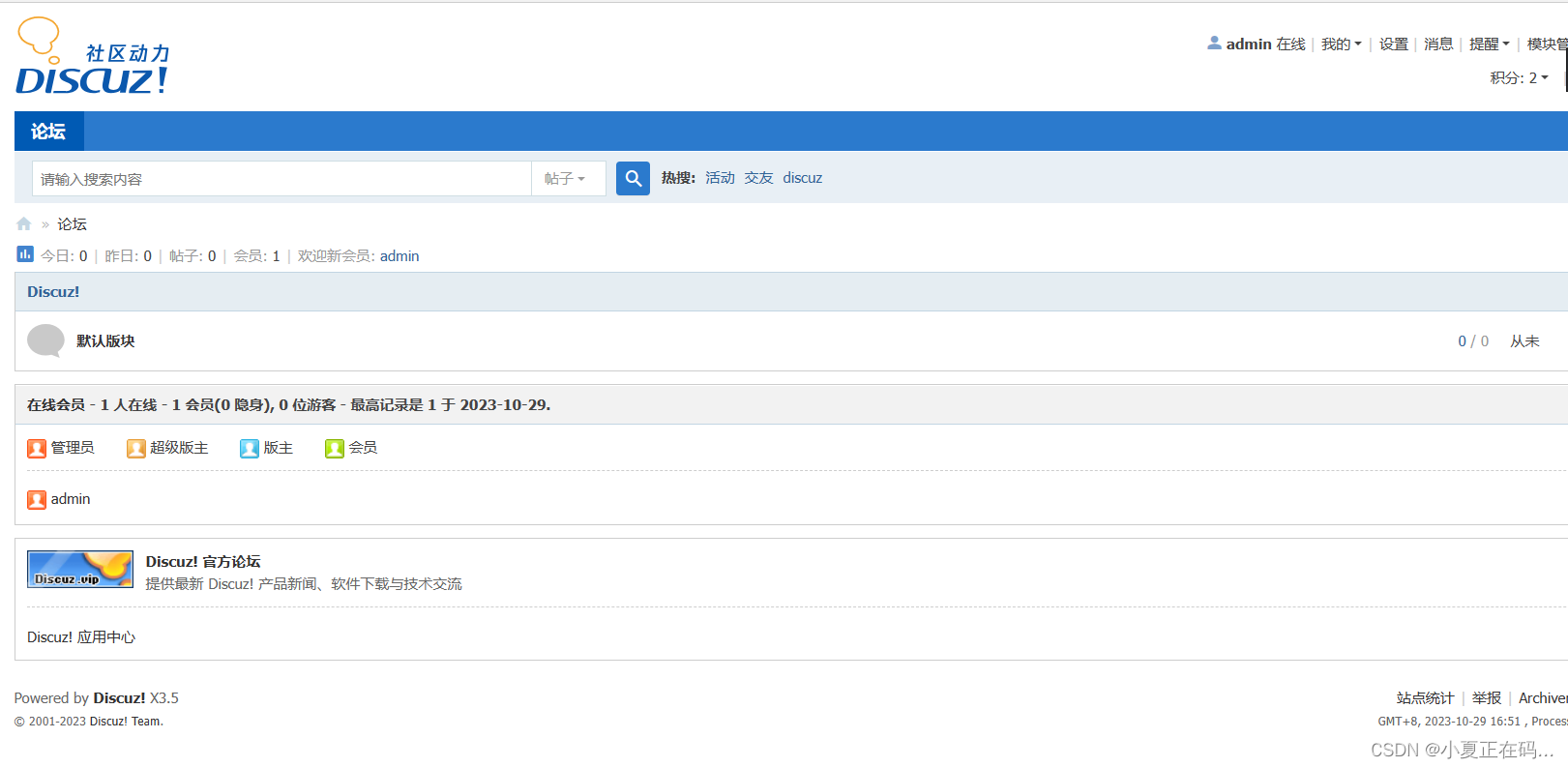
【redhat9.2】搭建Discuz-X3.5网站
步骤 1.配置软件仓库 2.安装对应的软件 httpd php* mariadb* 3.启动服务 httpd mariadb 4.配置数据库 创建数据库 修改root密码 数据库的 5.传源码包(Discuz-X3.5) 解压 6.web页面初始化 关闭防火墙 允许http服务通过 修改权限 实…...

算法篇 : 并查集
介绍 英文名:union find set 作用:合并集合,查询集合 合并:将有直接关系的顶点放在一个集合里面 查找:查询某个顶点所属的集合 集合的标志:用祖先点的标号作为每个集合的标识 案例 如果说将下图的集合2合并…...

AM@微积分基本定理@微积分第二基本定理
文章目录 abstract微积分第二基本定理微积分基本公式公式书写例 结合不定积分的方法求定积分定积分换元法证明 定积分换元公式逆用例 和不定积分第二类换元法的差别定积分分部积分法例 abstract 微积分第一基本定理告诉我们,总是能够通过积分法构造(表达)一个连续函数的原函数…...

goland常用快捷键
移动光标 控制光标的移动:fn上下左右 移至当前页的页头:ctrlPgUp 移至并选中光标到当前页头:ctrlshiftPgUp 移至当前页的页尾:ctrlPgDn 移至并选中当前光标到当前页尾:ctrlshiftPgDn 返回到当前的光标处…...

CSDN写文章时常见问题及技巧
CSDN写文章时常见问题及技巧 1.有序待续、更新中 1.有序 过程: 写 1.空格 ,注意“.”后加个空格就可以生成序号,随心所欲编辑了 待续、更新中 ————————————————————— 以上就是今日博客的全部内容了 创作不易,若对您有…...
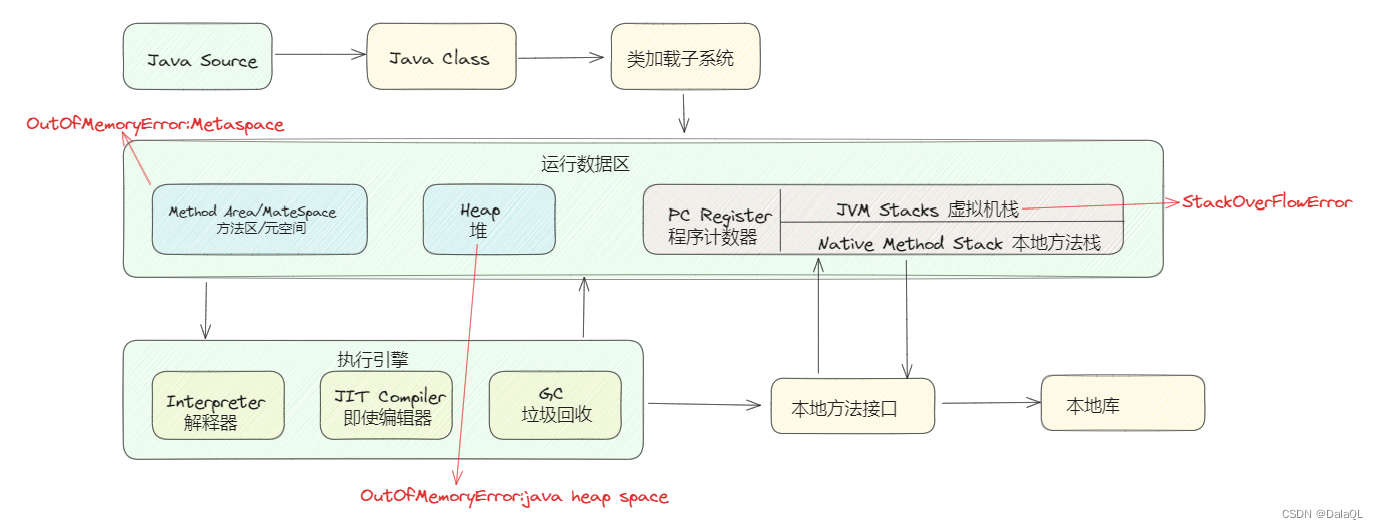
JVM虚拟机详解
目录 01JVM由哪些部分组成/运行流程 什么是程序计数器 详细介绍堆 介绍方法区(Method Area) 直接内存 虚拟机栈(Java Virtual machine Stacks) 垃圾回收是否涉及栈内存 栈内存分配越大越好吗 方法内的局部变量是否线程安全 什么情况下会导致栈…...

Go 怎么操作 OSS 阿里云对象存储
1 介绍 在项目开发中,我们经常会使用对象存储,比如 Amazon 的 S3,腾讯云的 COS,阿里云的 OSS 等。本文我们以阿里云 OSS 为例,介绍怎么使用 Go 操作对象存储。 阿里云 OSS 提供了 REST Api 和 OSS Go SDK࿰…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

数据结构第5章:树和二叉树完全指南(自整理详细图文笔记)
名人说:莫道桑榆晚,为霞尚满天。——刘禹锡(刘梦得,诗豪) 原创笔记:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 上一篇:《数据结构第4章 数组和广义表》…...

pgsql:还原数据库后出现重复序列导致“more than one owned sequence found“报错问题的解决
问题: pgsql数据库通过备份数据库文件进行还原时,如果表中有自增序列,还原后可能会出现重复的序列,此时若向表中插入新行时会出现“more than one owned sequence found”的报错提示。 点击菜单“其它”-》“序列”,…...

基于stm32F10x 系列微控制器的智能电子琴(附完整项目源码、详细接线及讲解视频)
注:文章末尾网盘链接中自取成品使用演示视频、项目源码、项目文档 所用硬件:STM32F103C8T6、无源蜂鸣器、44矩阵键盘、flash存储模块、OLED显示屏、RGB三色灯、面包板、杜邦线、usb转ttl串口 stm32f103c8t6 面包板 …...
