DAY38 动态规划 + 509. 斐波那契数 + 70. 爬楼梯 + 746. 使用最小花费爬楼梯
动态规划理论
动态规划,Dynamic Programming, DP, 如果某一问题有很多重叠子问题,使用动态规划是最有效的。
所以动态规划中每一个状态一定是由上一个状态推导出来的,这一点就区分于贪心,贪心没有状态推导,而是从局部直接选最优的,
状态转移公式(递推公式)是很重要,但动规不仅仅只有递推公式。
对于动态规划问题,我将拆解为如下五步曲,这五步都搞清楚了,才能说把动态规划真的掌握了!
- 确定dp数组(dp table)以及下标的含义
- 确定递推公式
- dp数组如何初始化
- 确定遍历顺序
- 举例推导dp数组
509. 斐波那契数
题目要求:斐波那契数,通常用 F(n) 表示,形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始,后面的每一项数字都是前面两项数字的和。也就是: F(0) = 0,F(1) = 1 F(n) = F(n - 1) + F(n - 2),其中 n > 1 给你n ,请计算 F(n) 。
思路
动规五部曲:
这里我们要用一个一维dp数组来保存递归的结果
- 确定dp数组以及下标的含义 dp[i]的定义为:第i个数的斐波那契数值是dp[i]
- 确定递推公式 状态转移方程 dp[i] = dp[i - 1] + dp[i - 2];
- dp数组如何初始化 dp[0] = 0; dp[1] = 1;
- 确定遍历顺序,从前向后遍历
- 举例推导 根据公式当n=10时,数列为0 1 1 2 3 5 8 13 21 34 55
class Solution {
public:int fib(int n) {if (n <= 1) return n;vector<int> dp(n+1);dp[0] = 0;dp[1] = 1;for (int i = 2; i <= n; ++i) {dp[i] = dp[i-1] + dp[i-2];}return dp[n];}
};70. 爬楼梯
题目要求:
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
注意:给定 n 是一个正整数。
思路
上第i个台阶的方法数=上第i-1个台阶的方法数(爬1个台阶)+上第i-2个台阶的方法数(爬2个台阶)
class Solution {
public:int climbStairs(int n) {if (n<=1) return n;int dp[3];dp[1] = 1;dp[2] = 2;for (int i = 3; i <= n; ++i) {int sum = dp[1] + dp[2];dp[1] = dp[2];dp[2] = sum;}return dp[2];}
};746. 使用最小花费爬楼梯
题目要求:数组的每个下标作为一个阶梯,第 i 个阶梯对应着一个非负数的体力花费值 cost[i](下标从 0 开始)。
每当你爬上一个阶梯你都要花费对应的体力值,一旦支付了相应的体力值,你就可以选择向上爬一个阶梯或者爬两个阶梯。
请你找出达到楼层顶部的最低花费。在开始时,你可以选择从下标为 0 或 1 的元素作为初始阶梯。
思路
修改之后的题意就比较明确了,题目中说 “你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯” 也就是相当于 跳到 下标 0 或者 下标 1 是不花费体力的, 从 下标 0 下标1 开始跳就要花费体力了。
- 确定dp数组以及下标的含义
使用动态规划,就要有一个数组来记录状态,本题只需要一个一维数组dp[i]就可以了。
dp[i]的定义:到达第i台阶所花费的最少体力为dp[i]。
- 确定递推公式
可以有两个途径得到dp[i],一个是dp[i-1] 一个是dp[i-2]。
dp[i - 1] 跳到 dp[i] 需要花费 dp[i - 1] + cost[i - 1]。
dp[i - 2] 跳到 dp[i] 需要花费 dp[i - 2] + cost[i - 2]。
那么究竟是选从dp[i - 1]跳还是从dp[i - 2]跳呢?
一定是选最小的,所以dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);
- dp数组如何初始化
看一下递归公式,dp[i]由dp[i - 1],dp[i - 2]推出,既然初始化所有的dp[i]是不可能的,那么只初始化dp[0]和dp[1]就够了,其他的最终都是dp[0]dp[1]推出。
那么 dp[0] 应该是多少呢? 根据dp数组的定义,到达第0台阶所花费的最小体力为dp[0],那么有同学可能想,那dp[0] 应该是 cost[0],例如 cost = [1, 100, 1, 1, 1, 100, 1, 1, 100, 1] 的话,dp[0] 就是 cost[0] 应该是1。
这里就要说明本题力扣为什么改题意,而且修改题意之后 就清晰很多的原因了。
新题目描述中明确说了 “你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。” 也就是说 到达 第 0 个台阶是不花费的,但从 第0 个台阶 往上跳的话,需要花费 cost[0]。
所以初始化 dp[0] = 0,dp[1] = 0;
- 确定遍历顺序
因为是模拟台阶,而且dp[i]由dp[i-1]dp[i-2]推出,所以是从前到后遍历cost数组就可以了。
- 举例推导dp数组
拿示例2:cost = [1, 100, 1, 1, 1, 100, 1, 1, 100, 1] ,来模拟一下dp数组的状态变化,如下:
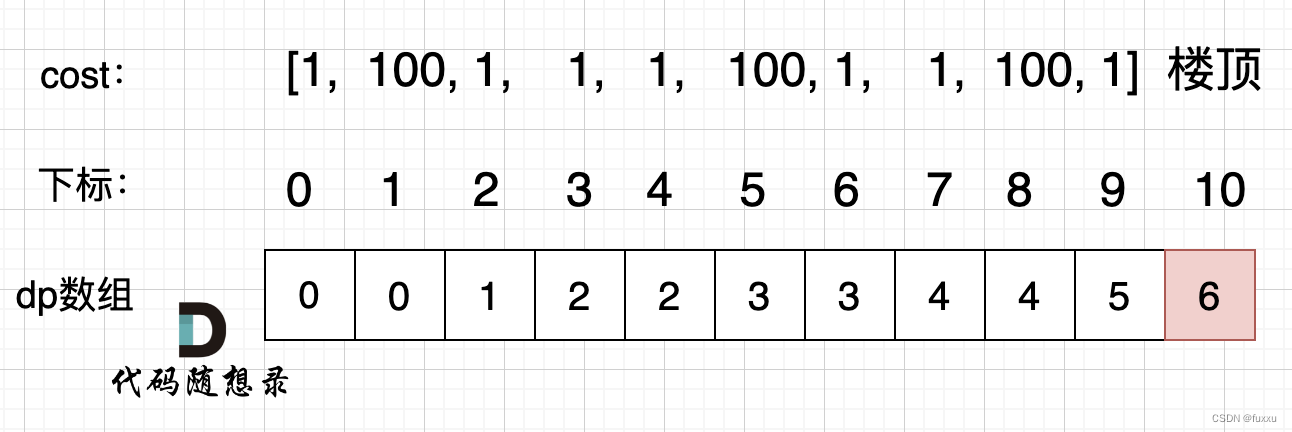
class Solution {
public:int minCostClimbingStairs(vector<int>& cost) {vector<int> dp(cost.size() + 1);dp[0] = 0;dp[1] = 0;for (int i = 2; i <= cost.size(); ++i) {dp[i] = min(dp[i-1] + cost[i-1], dp[i-2] + cost[i-2]);}return dp[cost.size()];}
};- 时间复杂度:O(n)
- 空间复杂度:O(n)
- 还可以优化空间复杂度,因为dp[i]就是由前两位推出来的,那么也不用dp数组了,优化方法和上一题同理。
相关文章:

DAY38 动态规划 + 509. 斐波那契数 + 70. 爬楼梯 + 746. 使用最小花费爬楼梯
动态规划理论 动态规划,Dynamic Programming, DP, 如果某一问题有很多重叠子问题,使用动态规划是最有效的。 所以动态规划中每一个状态一定是由上一个状态推导出来的,这一点就区分于贪心,贪心没有状态推导…...

Redis快速上手篇七(集群-一台虚拟机六个节点)
http://t.csdnimg.cn/S0NpK与上篇六个虚拟机配置基本一样有不懂可以看上篇配置实例 集群搭建 根据上篇文章,本篇只着重于小方面的配置差别 配置集群一般不要设置密码 1.搭建一台虚拟机后再安装目录下新建文件夹 redis_cluster 2.在文件夹内创建六个文…...
社恐了怎么办?如何改变社交恐惧症?
社恐这个词已经算是普及了,自嘲自己是社恐的人真的挺多的,好像一句我社恐了就能解析很多问题,其实真正的社恐远比我们想象的要痛苦多了,社恐能被更多人认识到本来是件好事,但是过于的用社恐来给自己贴标签,…...

HiQPdf Library for .NET - HTML to PDF Crack
HiQPdf Library for .NET - HTML 到 PDF 转换器 .NET Core,用于 .NET 的 HiQPdf HTML 到 PDF 转换器 :HiQPdf HTML to PDF Library for .NET C# 和 HTML to PDF .NET Core 为您提供了一个现代、快速、灵活且强大的工具,只需几行代码即可创建复…...

ES6中Set集合
ES6中的Set是一种数据结构,类似于数组,但是它的值都是唯一的。它是通过一组有序的、由唯一元素组成的集合实现的,不允许重复项。Set可以用于存储任何类型的数据,包括原始类型和复合类型,如对象和数组。 Set有以下特点…...

论坛介绍 | COSCon'23 开源文化(GL)
众多开源爱好者翘首期盼的开源盛会:第八届中国开源年会(COSCon23)将于 10月28-29日在四川成都市高新区菁蓉汇举办。本次大会的主题是:“开源:川流不息、山海相映”!各位新老朋友们,欢迎到成都&a…...
【httpd】 Apache http服务器目录显示不全解决
文章目录 1. 文件名过长问题1.1 在centos中文件所谓位置etc/httpd/conf.d/httpd-autoindex.conf1.2 在配置文件httpd-autoindex.conf中的修改:1.3 修改完成后重启Apache: 1. 文件名过长问题 1.1 在centos中文件所谓位置etc/httpd/conf.d/httpd-autoindex…...
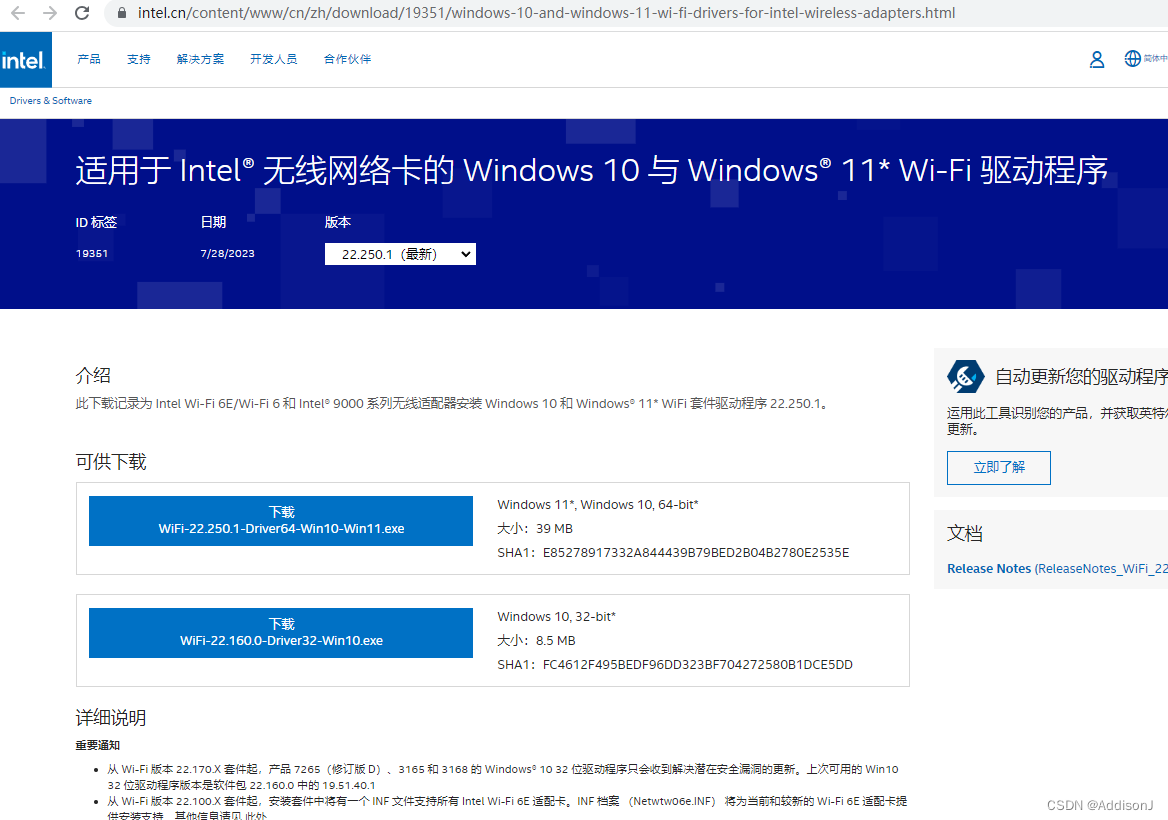
笔记本电脑搜索不到wifi6 无线路由器信号
路由器更换成wifi6 无线路由器后,手机能搜索到这个无线信号,但是笔记本搜索不到这个无线信号,后网上搜索后发现是无线网卡驱动问题,很多无线网卡使用的是Intel芯片,Intel就此发布了公告,升级驱动就可以彻底…...

js获取input?
在JavaScript中,获取输入框(通常指的是HTML的<input>元素)的值有多种方法。以下是其中的一些: 通过ID获取: javascriptvar inputValue document.getElementById(inputId).value; 这里,inputId 是…...
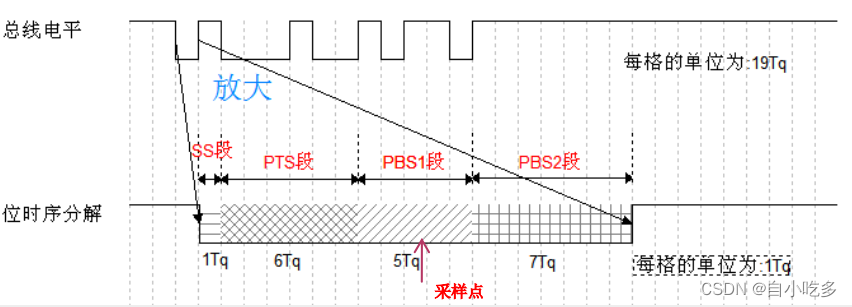
STM32 CAN使用
STM32 CAN使用 简介各种通讯接口对比报文总线上的报文信息表示为几种固定的赖类型数据帧列表模式掩码模式配置CAN配置参数位时序 简介 控制器局域网CAN(Controller Area Network)是由德国博世公司为汽车应用而开发的多主机局部网络,用于汽车的监测和控制…...

安全和便捷:如何将运营商二要素API应用于实名制管理中
引言 随着互联网的快速发展,数字化身份验证和实名制管理变得越来越重要。在金融、电子商务、社交媒体等领域,确保用户身份的安全和准确性至关重要。运营商二要素核验API成为了实名制管理的有力工具,它不仅能够提供高水平的安全性,…...
leetcode-二叉树
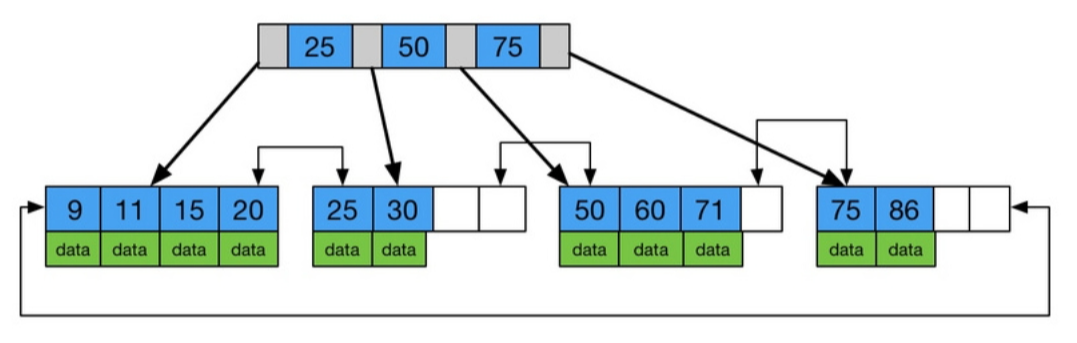
B树和B树的区别 B树,也即balance树,是一棵多路自平衡的搜索树。它类似普通的平衡二叉树,不同的一点是B树允许每个节点有更多的子节点。 B树内节点不存储数据,所有关键字都存储在叶子节点上。B树: B树: 二叉…...
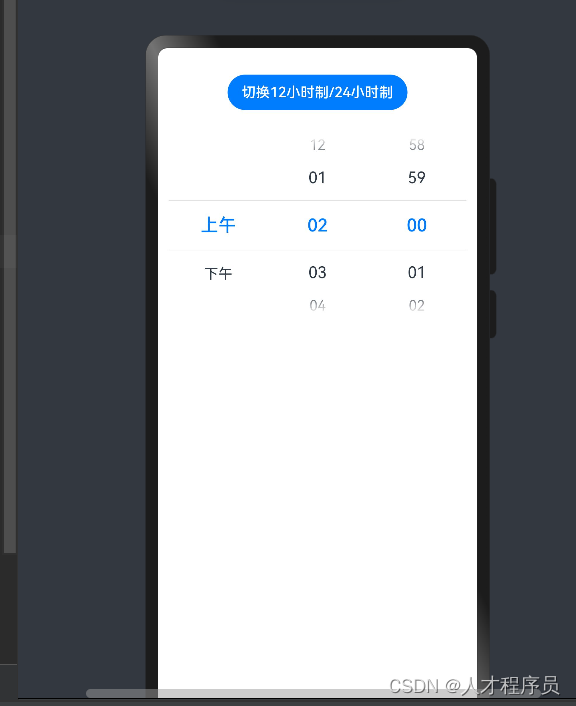
【鸿蒙软件开发】ArkTS基础组件之TextTimer(文本显示计时)、TimePicker(时间选择)
文章目录 前言一、TextTimer1.1 子组件1.2 接口参数TextTimerController 1.3 属性1.4 事件1.5 示例代码 二、TimePicker2.1 子组件2.2 接口参数 2.3 属性2.4 事件TimePickerResult对象说明 2.5 示例代码 总结 前言 通过文本显示计时信息并控制其计时器状态的组件。 时间选择组…...

pytorch 笔记:KLDivLoss
1 介绍 对于具有相同形状的张量 ypred 和 ytrue(ypred 是输入,ytrue 是目标),定义逐点KL散度为: 为了在计算时避免下溢问题,此KLDivLoss期望输入在对数空间中。如果log_targetTrue,则目标…...
父子项目打包发布至私仓库
父子项目打包发布至私仓库 1、方法一 在不需要发布至私仓的模块上添加如下代码: <plugin><groupId>org.apache.maven.plugins</groupId><artifactId>maven-deploy-plugin</artifactId><configuration><skip>true</s…...

汽车网络安全--ECU的安全更新
目前,汽车ECU的软件更新可以总结分成三大类: 工厂刷写模式:工厂大批量刷写或者升级,一般在出厂用; 工程模式:4S店、工厂等专业人员进行的ECU固件更新,通常是动力、转向、车控等; 车主模式:车主根据云端推送信息,通过IVI进行应用软件更新;目前也有趋势通过这种方式刷…...

NLP之搭建RNN神经网络
文章目录 代码展示代码意图代码解读知识点介绍1. Embedding2. SimpleRNN3. Dense 代码展示 # 构建RNN神经网络 from tensorflow.keras.models import Sequential from tensorflow.keras.layers import Dense, SimpleRNN, Embedding import tensorflow as tfrnn Sequential() …...

Android问题笔记四十三:JNI 开发如何快速定位崩溃问题
点击跳转>Unity3D特效百例点击跳转>案例项目实战源码点击跳转>游戏脚本-辅助自动化点击跳转>Android控件全解手册点击跳转>Scratch编程案例点击跳转>软考全系列 👉关于作者 专注于Android/Unity和各种游戏开发技巧,以及各种资源分享&…...
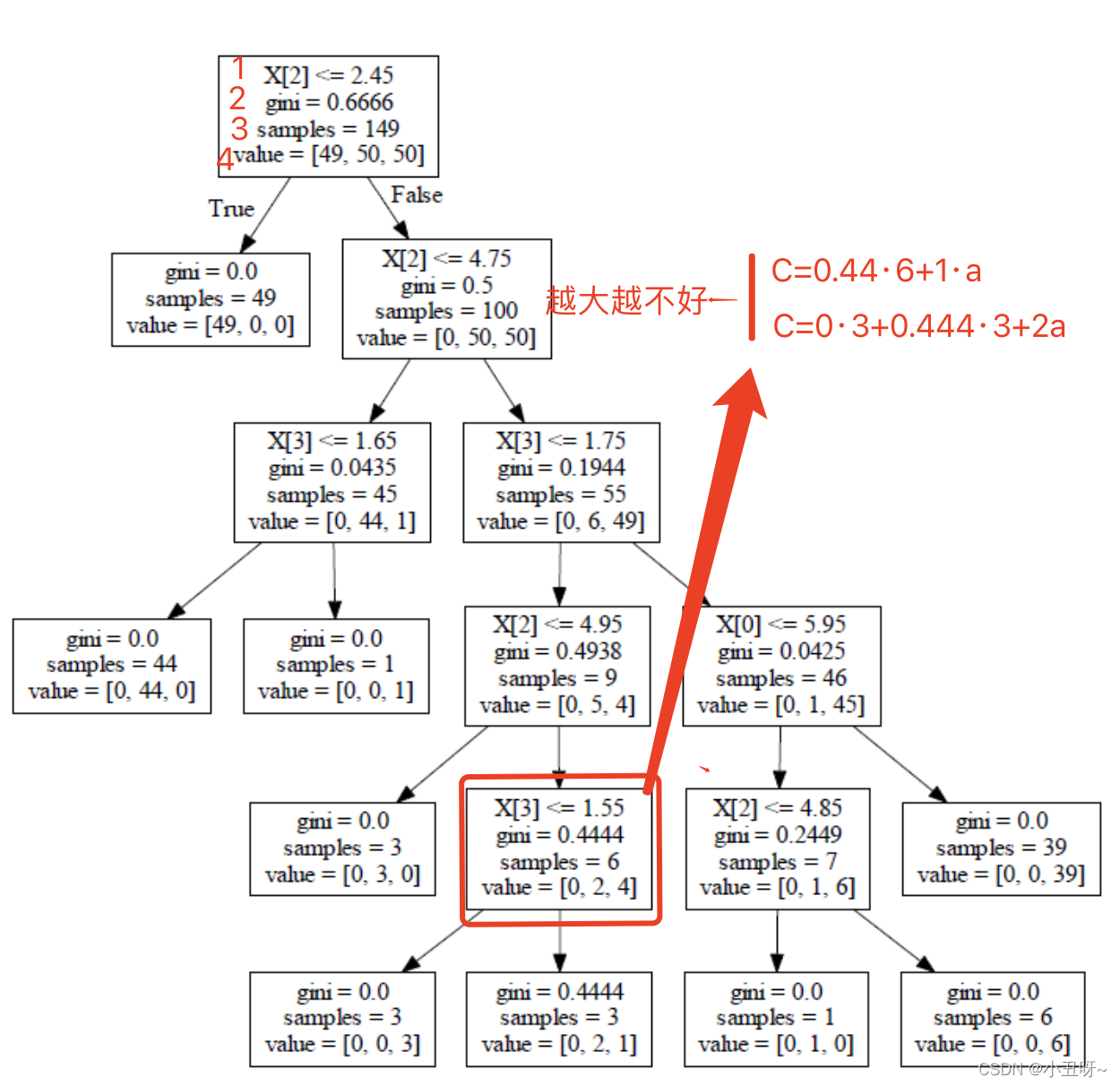
机器学习 | 决策树算法
一、决策树算法概述 1、树模型 决策树:从根节点开始一步步走到叶子节点(决策)。所有的数据最终都会落到叶子节点,既可以做分类也可以做回归。 在分类问题中,表示基于特征对实例进行分类的过程,可以认为是if-then的集合࿰…...

javascript中各种风骚的代码
1.判断数值符号是否相同 function numericSymbolsIsEqual(x: number, y: number): boolean {return (x ^ y) > 0}console.log(numericSymbolsIsEqual(1, 1))console.log(numericSymbolsIsEqual(-1, 1))console.log(numericSymbolsIsEqual(1, -1))console.log(numericSymbols…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...

MySQL 部分重点知识篇
一、数据库对象 1. 主键 定义 :主键是用于唯一标识表中每一行记录的字段或字段组合。它具有唯一性和非空性特点。 作用 :确保数据的完整性,便于数据的查询和管理。 示例 :在学生信息表中,学号可以作为主键ÿ…...

基于PHP的连锁酒店管理系统
有需要请加文章底部Q哦 可远程调试 基于PHP的连锁酒店管理系统 一 介绍 连锁酒店管理系统基于原生PHP开发,数据库mysql,前端bootstrap。系统角色分为用户和管理员。 技术栈 phpmysqlbootstrapphpstudyvscode 二 功能 用户 1 注册/登录/注销 2 个人中…...
