当前位置： 首页 > news >正文

共谈信创谋发展 | 开源网安主办的信创生态构建沙龙圆满完成

news 2026/2/9 6:24:41

​10月26日，由珠海市工业和信息化局、珠海市高新区科技创新和产业发展局指导，珠海华发产业园与开源网安珠海公司等联合主办的“赋能数字转型 提速国产替代”—Uni-Idea信创生态构建沙龙在华发·信创产业园成功举办，近百位行业代表参加本次活动，共同探信创产业未来的机遇与挑战。

活动上，开源网安与华发产业园签署战略合作，双方将共建信创人才培训服务平台，通过搭建线上课程平台、线下组织活动等方式，展开软件技术、项目管理、安全技术、安全管理等培训，助力信创行业人才素质提高，加快构建合作共生、互利共赢、生态共建的信创产业生态发展新格局。

开源网安事业部总经理胡要中针对“如何构建数智化业务场景安全底座”分享探索经验。胡要中认为，随着新一代互联网技术的广泛应用，产业数智化进程持续加速，网络空间安全问题也日益显现，其中软件安全问题尤为突出。开源网安通过网安云平台建立SaaS化的软件安全服务，帮助企业在数字化转型过程中，提升业务系统安全威胁感知与风险应对能力，塑造数智化业务场景安全底座，为构建安全韧性的数字化环境贡献力量。

作为科技创新的重要领域，信创产业正迎来新一轮发展机遇，市场空间显著增大。开源网安将与更多合作伙伴勠力同心，推动信创资源的整合和成果转化，打造自主可控的信创产业完整链条，为构建具有国际竞争力的信创人才队伍奠定坚实基础，为推动珠海乃至全国信创产业的持续发展注入强大动力。

推荐阅读：

硬核实力，再获认可 | 开源网安典型案例入选《ISC 2023软件供应链安全洞察》报告

产教融合共发展 | 开源网安高校合作战略再下一城

相关文章：

共谈信创谋发展 | 开源网安主办的信创生态构建沙龙圆满完成

​10月26日，由珠海市工业和信息化局、珠海市高新区科技创新和产业发展局指导，珠海华发产业园与开源网安珠海公司等联合主办的“赋能数字转型 提速国产替代”—Uni-Idea信创生态构建沙龙在华发信创产业园成功举办，近百位行业代表参加本次活动&…...

编程日记 2023/10/30 11:30:19

第四章认识Node.js模块化开发

Node.js系统模块 续上一篇文章第三章认识Node.js模块化开发-CSDN博客，这次继续来认识和总结以下node的常用模块开发 Node.js系统模块是指Node.js自带的一些模块，这些模块可以直接在Node.js中使用，无需安装其他包。以下是常用的Node.js系统模块…...

编程日记 2023/10/30 11:28:15

Widget必须在GUI线程中创建

背景：miniblink的vip版本，下载功能是独立线程，我希望在下载后弹出窗口，就在其中创建了QWidget子类对象。然后出现了上面的错误。 解决方法： 使用信号和槽来处理。 具体来讲，在独立线程中创建QObject子类…...

编程日记 2023/10/30 11:27:14

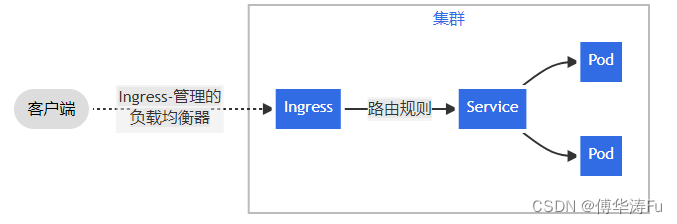
Kubernetes概念及实践

Kubernetes(K8S)中文文档_Kubernetes中文社区 Kubernetes 文档 | Kubernetes K8S 是负责自动化运维管理多个跨机器 Docker 程序的 集群。 kubeadm快速部署K8s集群的工具，如： 创建master node：kubeadm init 将worker node加入到集群中&#x…...

编程日记 2023/10/30 11:26:13

洛谷 B2007 A+B问题 C++代码

目录 题目描述 AC Code 题目描述 AC Code #include<bits/stdc.h> using namespace std; typedef long long ll; int main() { int a,b;cin>>a>>b;cout<<ab<<endl;return 0; }...

编程日记 2023/10/30 11:23:09

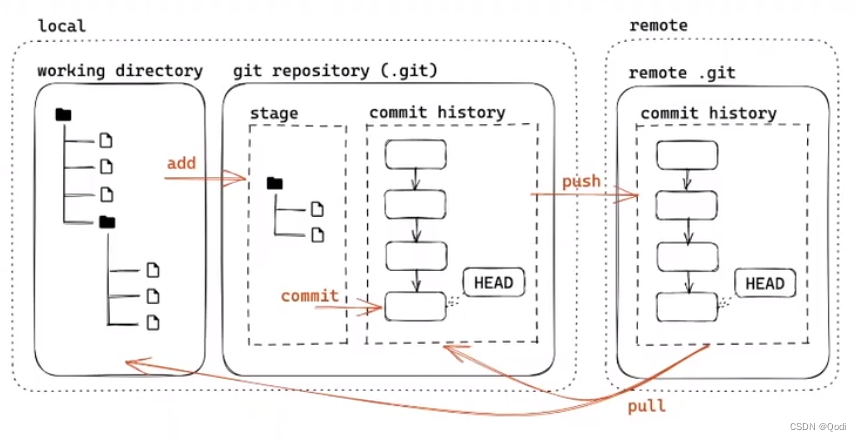
Git基础 | 原理、配置、用法、分支 合并

目录 1 git初步了解 1.1 git的安装 1.2 git原理模型 1.3 git基础配置 1.4 git基础用法 1 将文件加入暂存区 2 查看当前的git仓库状态 3 删除文件 4 commit 将暂存区文件加入本地git版本仓库 5 查看提交历史 更改 2 分支 2.1 创建分支 2.2 查看分支 2.3 切换分支 …...

编程日记 2023/10/30 11:22:07

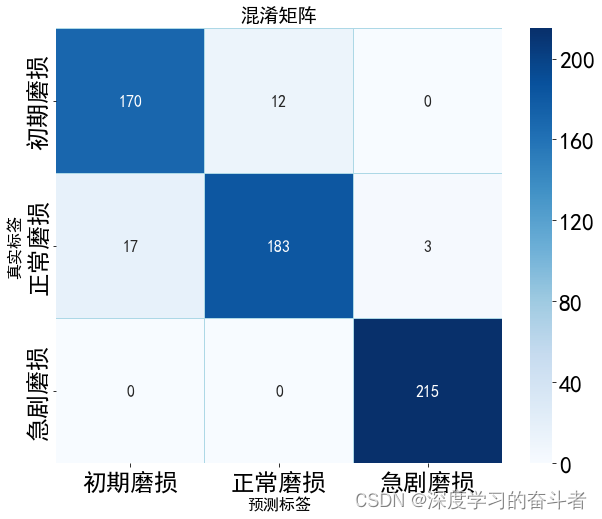
刀具磨损状态识别（Python代码，MSCNN_LSTM_Attention模型，初期磨损、正常磨损和急剧磨损分类，解压缩直接运行）

1.运行效果&#xff1a;刀具磨损状态识别&#xff08;Python代码&#xff0c;MSCNN_LSTM_Attention模型&#xff0c;初期磨损、正常磨损和急剧磨损&#xff09;_哔哩哔哩_bilibili 环境库&#xff1a; NumPy 版本: 1.19.4 Pandas 版本: 0.23.4 Matplotlib 版本: 2.2.3 Keras …...

编程日记 2023/10/30 11:20:06

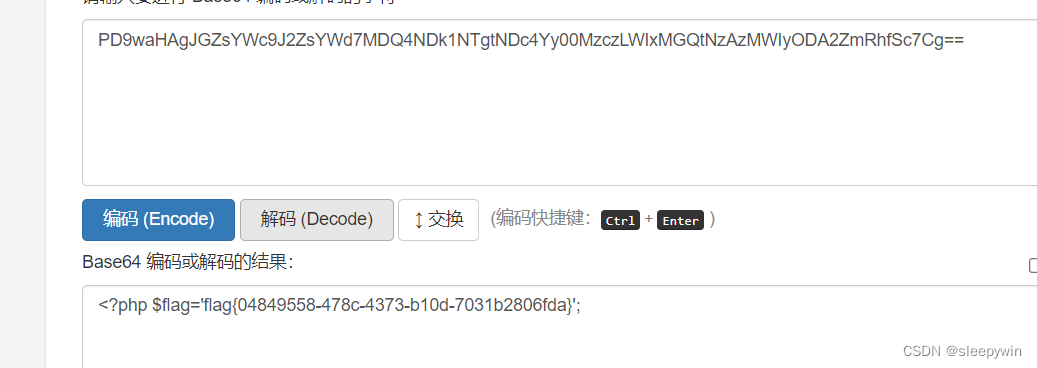
web：[网鼎杯 2020 青龙组]AreUSerialz

题目 点进题目发现 需要进行代码审计 function __destruct() {if($this->op "2")$this->op "1";$this->content "";$this->process();}这里有__destruct()函数&#xff0c;在对象销毁时自动调用&#xff0c;根据$op属性的值进行…...

编程日记 2023/10/30 11:18:58

【Python机器学习】零基础掌握PolynomialCountSketch内核近似特征

面临挑战的机器学习模型：如何提高准确性？ 在实际应用中，机器学习模型常常面临一个问题：如何在保持模型复杂性不变的情况下，提高模型的准确性？特别是在处理高维数据集时，这个问题尤为突出。这里，有一种名为“核方法”的技术可以解决这个问题，但通常会增加计算成本。那…...

编程日记 2023/10/30 11:17:57

【Linux】深入理解系统文件操作（1w字超详解）

1.系统下的文件操作&#xff1a; ❓是不是只有C\C有文件操作呢&#xff1f;&#x1f4a1;Python、Java、PHP、go也有&#xff0c;他们的文件操作的方法是不一样的啊 1.1对于文件操作的思考&#xff1a; 我们之前就说过了&#xff1a;文件内容属性 针对文件的操作就变成了对…...

编程日记 2023/10/30 11:15:55

echarts柱状图和折线图双图表配置项

{tooltip: {trigger: axis,axisPointer: { // 坐标轴指示器&#xff0c;坐标轴触发有效type: cross // 默认为直线&#xff0c;可选为&#xff1a;line | shadow}},legend: {data: [新增客户数, 新增客户两年内回款情况],type: scroll,selectedMode: false // 控制是否可以通过…...

编程日记 2023/10/30 11:12:39

【LVS实战】02 搭建一个LVS-NAT实验

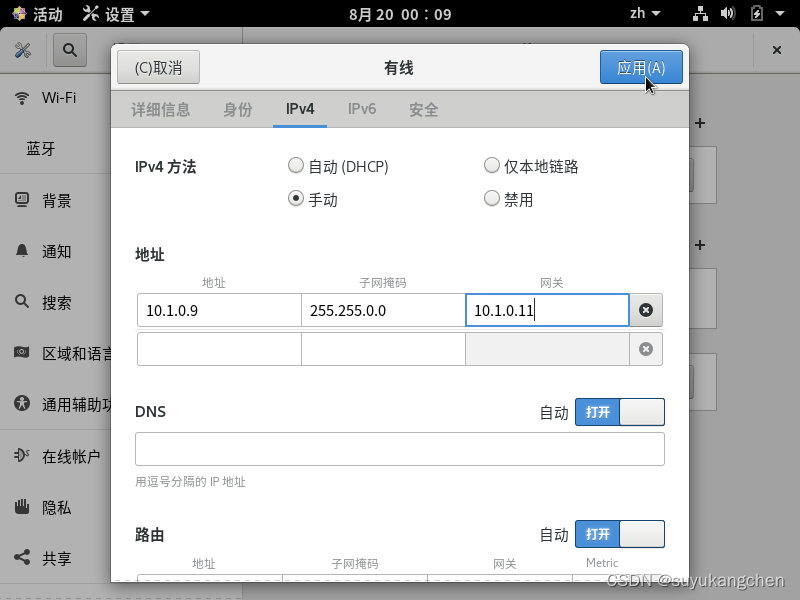
一、网络结构 用虚拟机搭建如下的几台机器&#xff0c;并配置如下的ip 关于虚拟机网卡和网络的配置&#xff0c;可以参考 iptables章节&#xff0c;05节&#xff1a;网络转发实验 主机A模拟外网的机器 B为负载均衡的机器 C和D为 RealServer 二、C和D主机的网关设置 C和D机…...

编程日记 2023/10/30 11:11:21

2023.10.26-SQL测试题

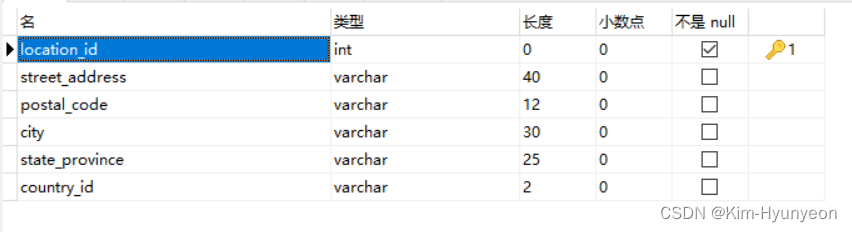
employee表&#xff1a; department表&#xff1a; job表&#xff1a; location表&#xff1a; 题目及答案&#xff1a; -- (1).查询工资大于一万的员工的姓名(first_name与last_name用“.”进行连接)和工资-- select CONCAT(first_name,.,last_name) as 姓名 ,salary -…...

编程日记 2023/10/30 11:10:20

JVM虚拟机：从结构到指令让你对栈有足够的认识

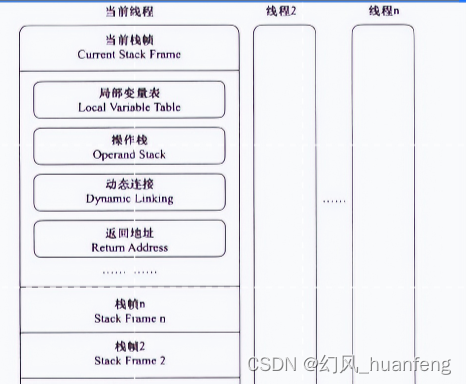
本文重点 在前面的课程中，我们学习了运行时数据区的大概情况，从本文开始，我们将对一些组件进行详细的介绍，本文我们将学习栈。栈内存主管java的运行，是在线程创建时创建的，它是线程私有的，它的生命周期是跟随线程的生命期，也就是说线程结束栈内存就释放了，对于栈来说…...

编程日记 2023/10/30 11:08:18

【启发式算法】白鲸优化算法【附python实现代码】

写在前面&#xff1a; 首先感谢兄弟们的订阅&#xff0c;让我有创作的动力&#xff0c;在创作过程我会尽最大能力&#xff0c;保证作品的质量&#xff0c;如果有问题&#xff0c;可以私信我&#xff0c;让我们携手共进&#xff0c;共创辉煌。 路虽远&#xff0c;行则将至&#…...

编程日记 2023/10/30 11:07:17

【Python机器学习】零基础掌握RBFSampler内核近似特征

有没有想过如何在复杂的数据集上快速进行分类？ 在现实生活中，大量的数据集通常非常复杂，并不总是线性可分的。例如，在医疗领域，诊断患者是否患有某种疾病通常涉及多个变量和复杂的模式。简单的线性模型可能无法有效地处理这种复杂性。 一种可能的解决方案是使用更复杂的…...

编程日记 2023/10/30 11:03:58

高级工技能等级认定---网络设备安全

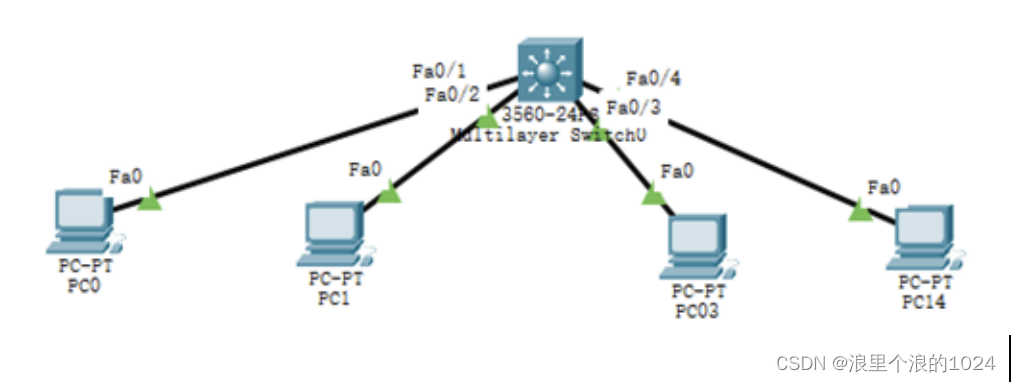
目录 一、DHCP 安全配置 二、SSH配置 三、标准ACL的配置 四、配置交换机端口安全 五、三层交换和ACL的配置 一、DHCP 安全配置 配置要求&#xff1a; 1.给交换机配置enable密码. 2.在交换机上创建VLAN 100&#xff0c;将F0/1-3口改为Access口&#xff0c;并加入到VLAN …...

编程日记 2023/10/30 11:02:57

spting Boot常见知识点

31.介绍一下 SpringBoot&#xff0c;有哪些优点&#xff1f; 1、Spring Boot 基于 Spring 开发&#xff0c;Spirng Boot 本身并不提供 Spring 框架的核心特性以及扩展功能&#xff0c;只是用于快速、敏捷地开发新一代基于 Spring 框架的应用程序。它并不是用来替代 Spring 的解…...

编程日记 2023/10/30 11:00:55

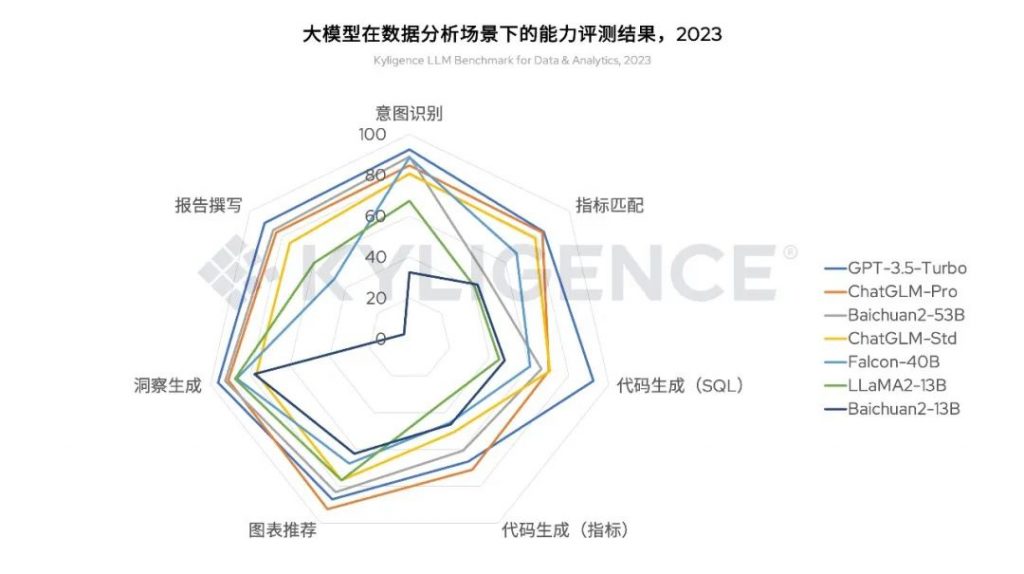
大模型在数据分析场景下的能力评测

“你们能对接国产大模型吗&#xff1f;” “开源的 LLaMA 能用吗&#xff0c;中文支持怎么样&#xff1f;” “私有化部署和在线服务哪个更合适&#xff1f;” 自 7 月 14 日发布 AI 数智助理 Kyligence Copilot 后&#xff0c;我们收到了很多类似上面的咨询&#xff0c;尤其…...

编程日记 2023/10/30 10:58:40

[笔记] 关于y1变量取名冲突的问题

参考博客 遇到的问题和这位老哥的一模一样。 结论是&#xff1a;当我们用math头文件的时候&#xff0c;不能在全局定义 y0 和 y1&#xff0c;j0、j1、jn、yn。...

编程日记 2023/10/30 10:57:39

k8s从入门到放弃之Ingress七层负载

k8s从入门到放弃之Ingress七层负载 在Kubernetes&#xff08;简称K8s&#xff09;中&#xff0c;Ingress是一个API对象&#xff0c;它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress&#xff0c;你可…...

编程新知 2025/9/7 0:12:53

逻辑回归：给不确定性划界的分类大师

想象你是一名医生。面对患者的检查报告&#xff08;肿瘤大小、血液指标&#xff09;&#xff0c;你需要做出一个**决定性判断**&#xff1a;恶性还是良性&#xff1f;这种“非黑即白”的抉择&#xff0c;正是**逻辑回归&#xff08;Logistic Regression&#xff09;** 的战场&a…...

编程新知 2025/10/27 21:25:04

基础测试工具使用经验

背景 vtune&#xff0c;perf, nsight system等基础测试工具&#xff0c;都是用过的&#xff0c;但是没有记录&#xff0c;都逐渐忘了。所以写这篇博客总结记录一下&#xff0c;只要以后发现新的用法&#xff0c;就记得来编辑补充一下 perf 比较基础的用法&#xff1a; 先改这…...

编程新知 2025/11/22 7:38:58

Linux-07 ubuntu 的 chrome 启动不了

文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了&#xff0c;报错如下四、启动不了&#xff0c;解决如下 总结 问题原因 在应用中可以看到chrome&#xff0c;但是打不开(说明&#xff1a;原来的ubuntu系统出问题了&#xff0c;这个是备用的硬盘&a…...

编程新知 2026/1/29 17:56:19

06 Deep learning神经网络编程基础 激活函数 --吴恩达

深度学习激活函数详解 一、核心作用 引入非线性：使神经网络可学习复杂模式控制输出范围：如Sigmoid将输出限制在(0,1)梯度传递：影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

编程新知 2025/11/17 21:48:26

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南

1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发&#xff0c;使用DevEco Studio作为开发工具&#xff0c;采用Java语言实现&#xff0c;包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...

编程新知 2025/12/19 22:56:05

音视频——I2S 协议详解

I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议&#xff0c;专门用于在数字音频设备之间传输数字音频数据。它由飞利浦&#xff08;Philips&#xff09;公司开发&#xff0c;以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...

编程新知 2026/2/1 2:08:53

作为测试我们应该关注redis哪些方面

1、功能测试 数据结构操作&#xff1a;验证字符串、列表、哈希、集合和有序的基本操作是否正确 持久化&#xff1a;测试aof和aof持久化机制&#xff0c;确保数据在开启后正确恢复。 事务&#xff1a;检查事务的原子性和回滚机制。 发布订阅&#xff1a;确保消息正确传递。 2、性…...

编程新知 2025/11/1 2:00:51

【深度学习新浪潮】什么是credit assignment problem？

Credit Assignment Problem（信用分配问题） 是机器学习，尤其是强化学习（RL）中的核心挑战之一，指的是如何将最终的奖励或惩罚准确地分配给导致该结果的各个中间动作或决策。在序列决策任务中，智能体执行一系列动作后获得一个最终奖励，但每个动作对最终结果的贡献程度往往…...

编程新知 2026/1/30 14:23:04

Neko虚拟浏览器远程协作方案：Docker+内网穿透技术部署实践

前言&#xff1a;本文将向开发者介绍一款创新性协作工具——Neko虚拟浏览器。在数字化协作场景中&#xff0c;跨地域的团队常需面对实时共享屏幕、协同编辑文档等需求。通过本指南&#xff0c;你将掌握在Ubuntu系统中使用容器化技术部署该工具的具体方案&#xff0c;并结合内网…...

编程新知 2026/1/27 9:02:37