贝叶斯变分方法:初学者指南--平均场近似
Eric Jang: A Beginner's Guide to Variational Methods: Mean-Field Approximation (evjang.com)
一、说明
变分贝叶斯 (VB) 方法是统计机器学习中非常流行的一系列技术。VB 方法允许我们将 统计推断 问题(即,给定另一个随机变量的值来推断随机变量的值)重写为优化 问题(即,找到最小化某些目标函数的参数值),本文将阐述这种精妙模型。
二、文章绪论
2.1 VB的概念
这种推理-优化二元性非常强大,因为它允许我们使用最新、最好的优化算法来解决统计机器学习问题(反之亦然,使用统计技术最小化函数)。
这篇文章是变分方法的介绍性教程。我将导出最简单的 VB 方法的优化目标,称为平均场近似。这个目标,也称为 变分下界,与变分自编码器中使用的目标完全相同(一篇简洁的论文,我将在后续文章中对其进行解释)。
2.2 本文目录
- 预备知识和符号
- 问题表述
- 平均场近似的变分下界
- 正向 KL 与反向 KL
- 与深度学习的联系
三、预备知识和符号
本文假设读者熟悉随机变量、概率分布和期望等概念。 如果您忘记了一些东西,这里有一个回顾。机器学习和统计符号的标准化不是很好,因此在这篇文章中使用非常精确的符号会很有帮助:
- 大写X表示随机变量
- 大写P( X)表示该变量的概率分布
- 小写x∼P _ _( X)表示一个值X采样(~)从概率分布磷( X)通过一些生成过程。
- 小写p ( X)是分布的密度函数X。它是测度空间上的标量函数X。
- p ( X= x )(速记p ( x )) 表示在特定值下评估的密度函数X。
许多学术论文交替使用术语“变量”、“分布”、“密度”,甚至“模型”。这本身不一定是错误的,因为X,磷( X), 和p ( X)所有这些都通过一一对应来相互暗示。 然而,将这些词混合在一起会令人困惑,因为它们的类型不同(对函数进行采样没有意义,对分布进行积分也没有意义)。
我们将系统建模为随机变量的集合,其中一些变量(X)是“可观察的”,而其他变量(Z)是“隐藏的”。我们可以通过下图来画出这种关系:
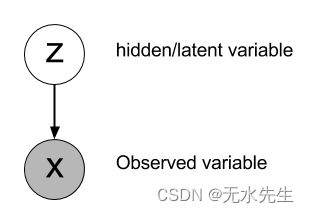
边缘绘制自Z到X通过条件分布将两个变量联系在一起磷( X| Z)。
X=



其中的各个部分都与通用名称相关联:
p ( Z| X)是后验概率:“给定图像,这是一只猫的概率是多少?” 如果我们可以从z∼ P( Z| X),我们可以用它来制作一个猫分类器,告诉我们给定的图像是否是猫。
p ( X| Z)是可能性:“给定值为Z 这计算了该图像的“可能性”X属于该类别({“is-a-cat”/“is-not-a-cat”})。如果我们可以从x∼P _ _( X| Z),然后我们生成猫的图像和非猫的图像就像生成随机数一样容易。如果您想了解更多信息,请参阅我关于生成模型的其他文章:[1]、[2]。
p ( Z)是先验概率。这捕获了我们所知道的任何先前信息Z- 例如,如果我们认为现有的所有图像中有 1/3 是猫,那么p ( Z= 1 ) =13和p ( Z= 0 ) =23。
3.1 作为先验的隐藏变量
这是感兴趣的读者的旁白。跳到下一部分继续学习本教程。
前面的猫示例展示了观察变量、隐藏变量和先验的非常传统的示例。然而,重要的是要认识到隐藏变量/观察变量之间的区别有些任意,并且您可以随意分解图形模型。
我们可以通过交换术语来重写贝叶斯定理:
所讨论的“后”是现在磷( X| Z)。隐藏变量可以从贝叶斯统计
框架 解释 为 附加到观察到的变量的先验信念。例如,如果我们相信X是多元高斯分布,隐藏变量Z可能代表高斯分布的均值和方差。参数分布磷( Z)那么 先验 分布为磷( X)。
您还可以自由选择哪些值X和Z代表。例如,Z可以改为“平均值、方差的立方根,以及X+ Y在哪里是∼ N( 0 , 1 )”。这有点不自然和奇怪,但结构仍然有效,只要磷( X| Z)进行相应修改。
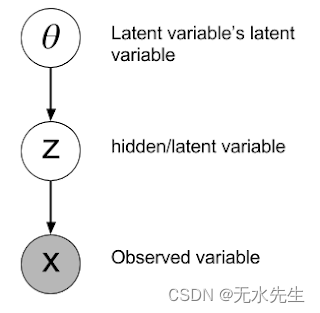
您甚至可以向系统“添加”变量。先验本身可能依赖于其他随机变量磷( Z| θ),它们有自己的先验分布磷( θ ),并且那些仍然有先验,等等。任何超参数都可以被认为是先验。在贝叶斯统计中, 先验一直向下。
3.2 问题表述
我们感兴趣的关键问题是后验推理,或者隐藏变量的计算函数。Z。后验推理的一些典型例子:
- 鉴于这段监控录像X,嫌疑人出现在其中吗?
- 鉴于此推特提要X,作者郁闷吗?
- 鉴于历史股价X1 : t − 1,什么会Xt是?
问题是,对于上面这样的复杂任务,我们通常不知道如何从中采样磷( Z| X)或计算p ( X| Z)。或者,我们可能知道以下形式p ( Z| X),但相应的计算非常复杂,我们无法在合理的时间内对其进行评估。我们可以尝试使用基于采样的方法,例如MCMC,但这些方法收敛速度很慢。
四、平均场近似的变分下界
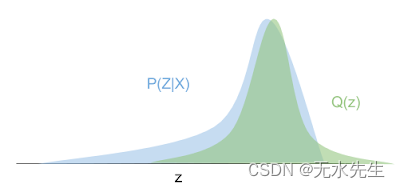
变分推理背后的想法是这样的:让我们对一个简单的参数分布进行推理问φ( Z| X)(如高斯)我们知道如何进行后验推理,但调整参数φ以便问φ是一样接近磷尽可能。
下面直观地说明了这一点:蓝色曲线是真正的后验分布,绿色分布是我们通过优化拟合到蓝色密度的变分近似(高斯)。
反向 KL 散度衡量信息量(以 nat 或单位为单位)需要“扭曲”
使其适应
。我们希望最大限度地减少这个数量
。
根据条件分布的定义, 。让我们把这个表达式替换成我们原来的表达式KL表达式,然后分布:
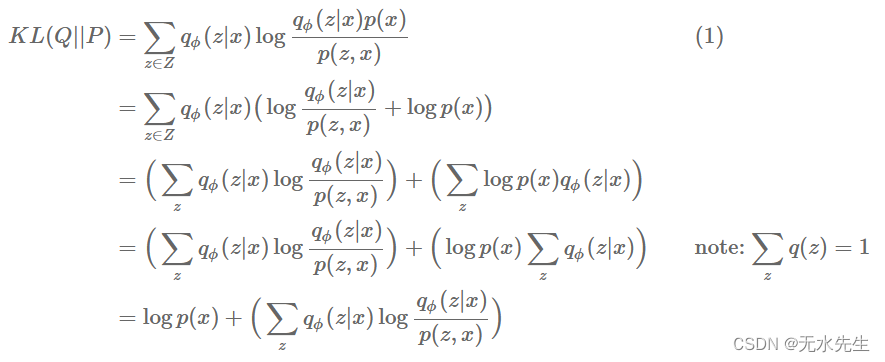
尽量减少 关于变分参数φ,我们只需最小化
, 因为
相对于固定φ。让我们将这个数量重写为分布的期望
。
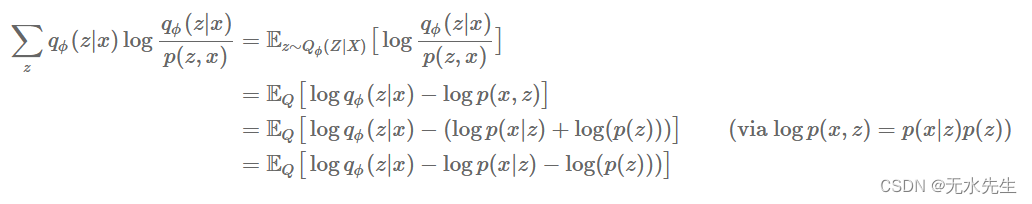
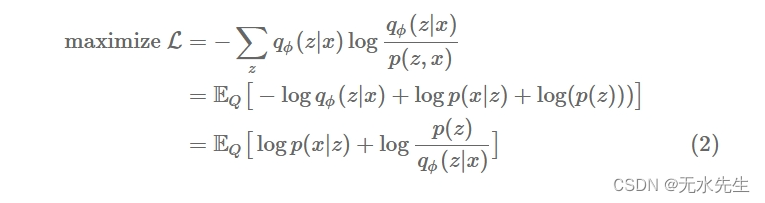
在文学中,被称为变分下界,并且如果我们可以评估,则在计算上是易于处理的
。我们可以进一步重新排列术语,产生直观的公式:
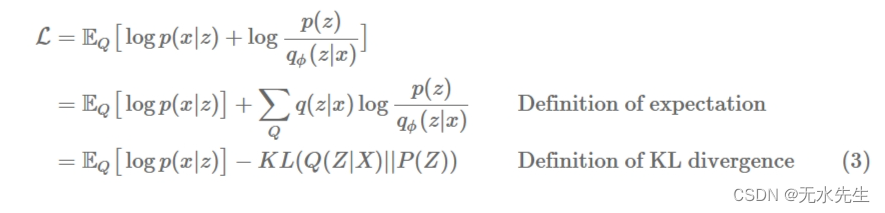
如果抽样 是一个转换观察结果的“编码”过程X到潜在代码z,然后采样
是一个“解码”过程,从z。
它遵循L是预期“解码”可能性的总和(我们的变分分布可以解码样本的效果如何)Z回到样本X),加上变分近似与先验之间的 KL 散度Z。如果我们假设Q (Z| X)是条件高斯的,然后先验Z通常选择均值为 0、标准差为 1 的对角高斯分布。
为什么L称为变分下界?替代L回到方程。(1),我们有:
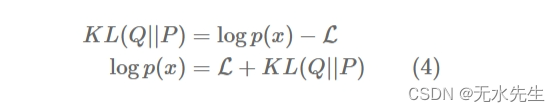
自从KL ( Q | | P) ≥ 0,日志p ( x )必须大于L。所以L是下界_日志p ( x )。L也称为证据下界 (ELBO),通过替代公式:
注意L本身包含近似后验和先验之间的 KL 散度项,因此总共有两个 KL 项日志p ( x )。
4.1 正向 KL 与反向 KL
KL散度不是对称 距离函数,即
我真的很喜欢 Kevin Murphy 在PML 教科书中的解释,我将尝试在这里重新表述:
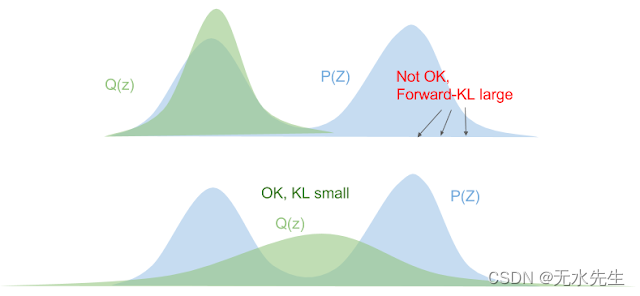
让我们首先考虑前锋 KL。正如我们从上面的推导中看到的,我们可以将 KL 写成“惩罚”函数的期望通过权重函数p ( z)。
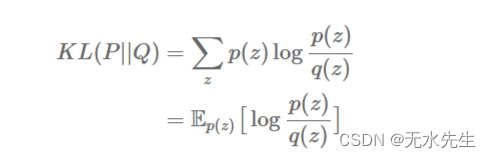
因此,当我们确保 无论在哪里
。优化的变分分布
被称为“避免零”(当密度避免为零时p ( Z)为零)。
最小化 Reverse-KL 具有完全相反的行为:
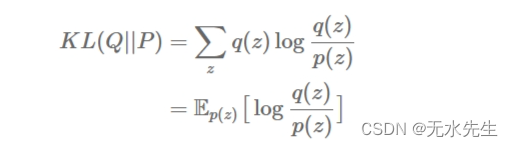
如果p ( Z) = 0,我们必须保证权重函数q( Z) = 0无论分母在哪里p ( Z) = 0,否则 KL 就会爆炸。这称为“迫零”:
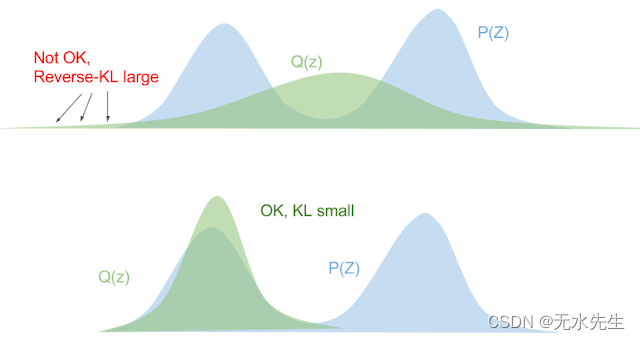
总而言之,最小化前向 KL 会“拉伸”你的变分分布Q (Z)覆盖整个P( Z)就像防水布一样,同时最大限度地减少反向KL“挤压”Q (Z) 在下面 P( Z)。
在机器学习问题中使用平均场近似时,请务必牢记使用反向 KL 的含义。如果我们将单峰分布拟合到多峰分布,我们最终会得到更多的假阴性(实际上有概率质量P( Z)我们认为没有的地方Q (Z))。
4.2 与深度学习的联系
变分方法对于深度学习非常重要。我将在后面的文章中详细阐述,但这里有一个快速剧透:
- 深度学习非常擅长使用大量数据对非常大的参数空间进行优化(特别是梯度下降)。
- 变分贝叶斯为我们提供了一个框架,通过它我们可以将统计推理问题重写为优化问题。
感谢您的阅读,敬请关注!
相关文章:

贝叶斯变分方法:初学者指南--平均场近似
Eric Jang: A Beginners Guide to Variational Methods: Mean-Field Approximation (evjang.com) 一、说明 变分贝叶斯 (VB) 方法是统计机器学习中非常流行的一系列技术。VB 方法允许我们将 统计推断 问题(即,给定另一个随机变量的值来推断随机变量的值&…...

Node学习笔记之user用户API模块
1、获取用户的基本信息 步骤 获取登录会话存储的session中用户的id判断是否获取到id根据用户id查询数据库中的个人信息检查指定 id 的用户是否存在将密码设置为空将数据返回给前端 // 获取用户信息数据 exports.userinfo (req, res) > {(async function () {// 1. 获取…...

智慧公厕:为公众提供全新的公共厕所使用体验
智慧公厕管理系统通过智能化技术的应用,为公众提供了全新的公厕使用体验。不仅仅是一个普通的提供“方便”的公共设施,智慧公厕更融合了精准环境监测、厕位占用监测、设备状态实时监控等功能,同时还提供了自动化清洁、灯光照明、除臭杀菌消毒…...

共谈信创谋发展 | 开源网安主办的信创生态构建沙龙圆满完成
10月26日,由珠海市工业和信息化局、珠海市高新区科技创新和产业发展局指导,珠海华发产业园与开源网安珠海公司等联合主办的“赋能数字转型 提速国产替代”—Uni-Idea信创生态构建沙龙在华发信创产业园成功举办,近百位行业代表参加本次活动&…...

第四章认识Node.js模块化开发
Node.js系统模块 续上一篇文章第三章认识Node.js模块化开发-CSDN博客,这次继续来认识和总结以下node的常用模块开发 Node.js系统模块是指Node.js自带的一些模块,这些模块可以直接在Node.js中使用,无需安装其他包。以下是常用的Node.js系统模块…...

Widget必须在GUI线程中创建
背景:miniblink的vip版本,下载功能是独立线程,我希望在下载后弹出窗口,就在其中创建了QWidget子类对象。然后出现了上面的错误。 解决方法: 使用信号和槽来处理。 具体来讲,在独立线程中创建QObject子类…...
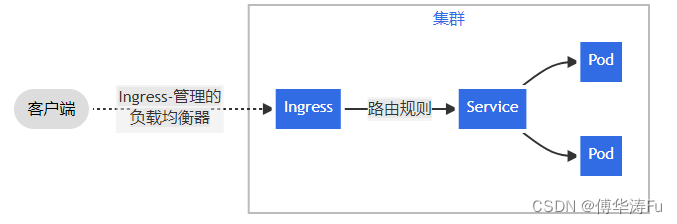
Kubernetes概念及实践
Kubernetes(K8S)中文文档_Kubernetes中文社区 Kubernetes 文档 | Kubernetes K8S 是负责自动化运维管理多个跨机器 Docker 程序的 集群。 kubeadm快速部署K8s集群的工具,如: 创建master node:kubeadm init 将worker node加入到集群中&#x…...

洛谷 B2007 A+B问题 C++代码
目录 题目描述 AC Code 题目描述 AC Code #include<bits/stdc.h> using namespace std; typedef long long ll; int main() { int a,b;cin>>a>>b;cout<<ab<<endl;return 0; }...
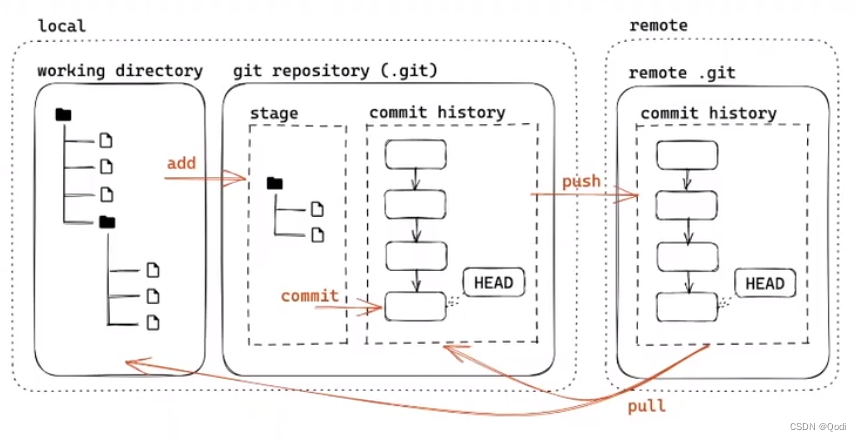
Git基础 | 原理、配置、用法、分支 合并
目录 1 git初步了解 1.1 git的安装 1.2 git原理模型 1.3 git基础配置 1.4 git基础用法 1 将文件加入暂存区 2 查看当前的git仓库状态 3 删除文件 4 commit 将暂存区文件加入本地git版本仓库 5 查看提交历史 更改 2 分支 2.1 创建分支 2.2 查看分支 2.3 切换分支 …...
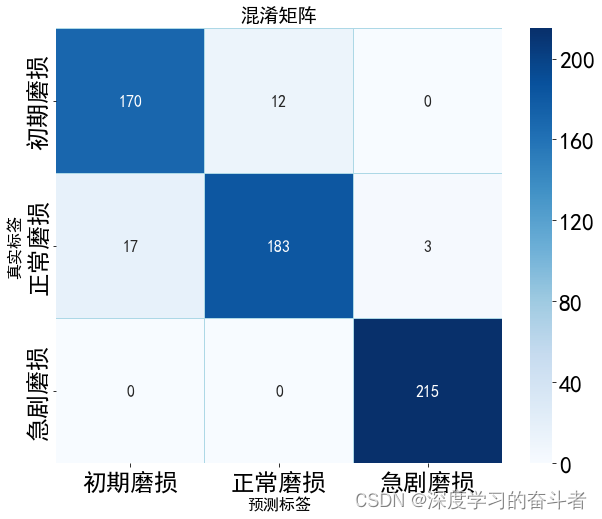
刀具磨损状态识别(Python代码,MSCNN_LSTM_Attention模型,初期磨损、正常磨损和急剧磨损分类,解压缩直接运行)
1.运行效果:刀具磨损状态识别(Python代码,MSCNN_LSTM_Attention模型,初期磨损、正常磨损和急剧磨损)_哔哩哔哩_bilibili 环境库: NumPy 版本: 1.19.4 Pandas 版本: 0.23.4 Matplotlib 版本: 2.2.3 Keras …...
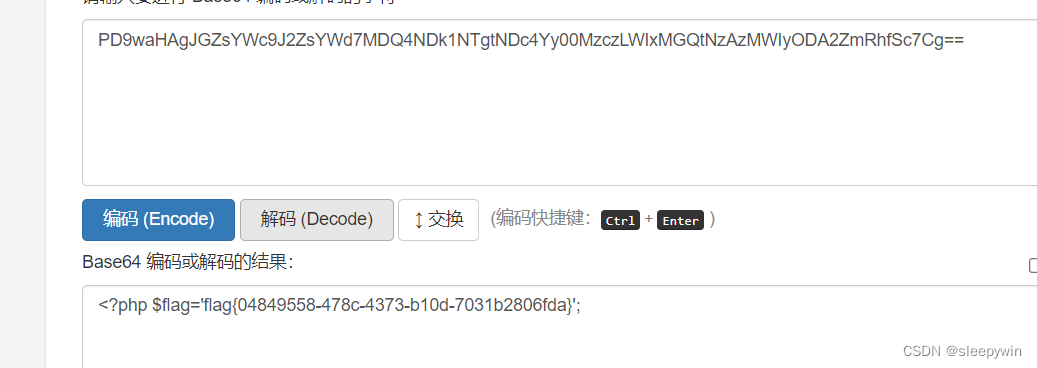
web:[网鼎杯 2020 青龙组]AreUSerialz
题目 点进题目发现 需要进行代码审计 function __destruct() {if($this->op "2")$this->op "1";$this->content "";$this->process();}这里有__destruct()函数,在对象销毁时自动调用,根据$op属性的值进行…...

【Python机器学习】零基础掌握PolynomialCountSketch内核近似特征
面临挑战的机器学习模型:如何提高准确性? 在实际应用中,机器学习模型常常面临一个问题:如何在保持模型复杂性不变的情况下,提高模型的准确性?特别是在处理高维数据集时,这个问题尤为突出。这里,有一种名为“核方法”的技术可以解决这个问题,但通常会增加计算成本。那…...

【Linux】深入理解系统文件操作(1w字超详解)
1.系统下的文件操作: ❓是不是只有C\C有文件操作呢?💡Python、Java、PHP、go也有,他们的文件操作的方法是不一样的啊 1.1对于文件操作的思考: 我们之前就说过了:文件内容属性 针对文件的操作就变成了对…...

echarts柱状图和折线图双图表配置项
{tooltip: {trigger: axis,axisPointer: { // 坐标轴指示器,坐标轴触发有效type: cross // 默认为直线,可选为:line | shadow}},legend: {data: [新增客户数, 新增客户两年内回款情况],type: scroll,selectedMode: false // 控制是否可以通过…...
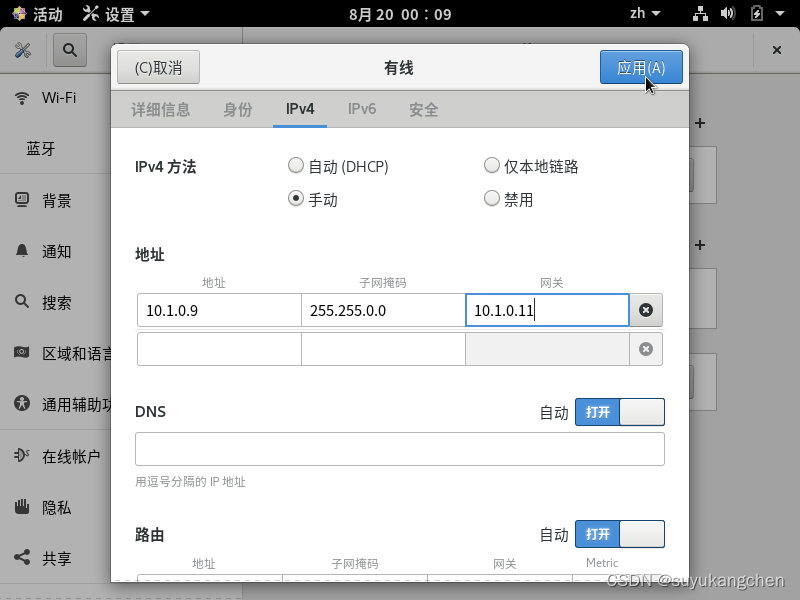
【LVS实战】02 搭建一个LVS-NAT实验
一、网络结构 用虚拟机搭建如下的几台机器,并配置如下的ip 关于虚拟机网卡和网络的配置,可以参考 iptables章节,05节:网络转发实验 主机A模拟外网的机器 B为负载均衡的机器 C和D为 RealServer 二、C和D主机的网关设置 C和D机…...
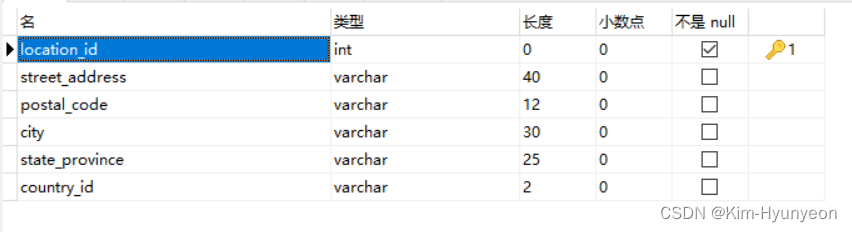
2023.10.26-SQL测试题
employee表: department表: job表: location表: 题目及答案: -- (1).查询工资大于一万的员工的姓名(first_name与last_name用“.”进行连接)和工资-- select CONCAT(first_name,.,last_name) as 姓名 ,salary -…...
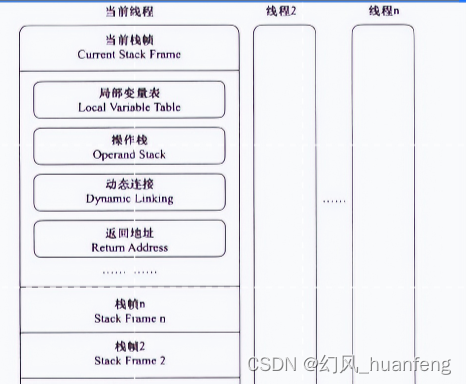
JVM虚拟机:从结构到指令让你对栈有足够的认识
本文重点 在前面的课程中,我们学习了运行时数据区的大概情况,从本文开始,我们将对一些组件进行详细的介绍,本文我们将学习栈。栈内存主管java的运行,是在线程创建时创建的,它是线程私有的,它的生命周期是跟随线程的生命期,也就是说线程结束栈内存就释放了,对于栈来说…...

【启发式算法】白鲸优化算法【附python实现代码】
写在前面: 首先感谢兄弟们的订阅,让我有创作的动力,在创作过程我会尽最大能力,保证作品的质量,如果有问题,可以私信我,让我们携手共进,共创辉煌。 路虽远,行则将至&#…...

【Python机器学习】零基础掌握RBFSampler内核近似特征
有没有想过如何在复杂的数据集上快速进行分类? 在现实生活中,大量的数据集通常非常复杂,并不总是线性可分的。例如,在医疗领域,诊断患者是否患有某种疾病通常涉及多个变量和复杂的模式。简单的线性模型可能无法有效地处理这种复杂性。 一种可能的解决方案是使用更复杂的…...
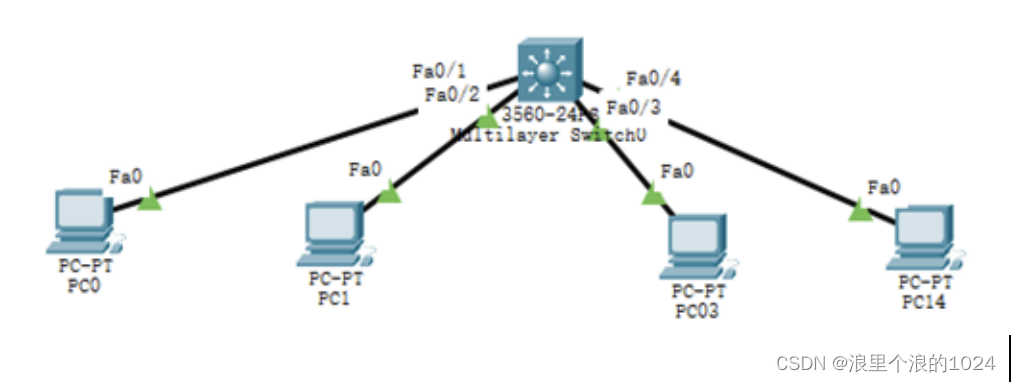
高级工技能等级认定---网络设备安全
目录 一、DHCP 安全配置 二、SSH配置 三、标准ACL的配置 四、配置交换机端口安全 五、三层交换和ACL的配置 一、DHCP 安全配置 配置要求: 1.给交换机配置enable密码. 2.在交换机上创建VLAN 100,将F0/1-3口改为Access口,并加入到VLAN …...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

【JavaSE】多线程基础学习笔记
多线程基础 -线程相关概念 程序(Program) 是为完成特定任务、用某种语言编写的一组指令的集合简单的说:就是我们写的代码 进程 进程是指运行中的程序,比如我们使用QQ,就启动了一个进程,操作系统就会为该进程分配内存…...

Sklearn 机器学习 缺失值处理 获取填充失值的统计值
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 使用 Scikit-learn 处理缺失值并提取填充统计信息的完整指南 在机器学习项目中,数据清…...

JS红宝书笔记 - 3.3 变量
要定义变量,可以使用var操作符,后跟变量名 ES实现变量初始化,因此可以同时定义变量并设置它的值 使用var操作符定义的变量会成为包含它的函数的局部变量。 在函数内定义变量时省略var操作符,可以创建一个全局变量 如果需要定义…...

CppCon 2015 学习:REFLECTION TECHNIQUES IN C++
关于 Reflection(反射) 这个概念,总结一下: Reflection(反射)是什么? 反射是对类型的自我检查能力(Introspection) 可以查看类的成员变量、成员函数等信息。反射允许枚…...
