NOIP2023模拟6联测27 旅行
题目大意
有一个有 n n n个点 n n n条边的无向连通图,一开始每条边都有一个颜色 c c c。
有 m m m次操作,每次操作将一条两个端点为 x , y x,y x,y的边的颜色修改为 c c c。求每次修改之后,图中有多少个颜色相同的连通块。
一个颜色相同的连通块指的是一个由一些相同颜色的边组成的连通块。
有 T T T组数据。
1 ≤ T ≤ 10 , 3 ≤ n , m ≤ 1 0 5 , 1 ≤ c ≤ n 1\leq T\leq 10,3\leq n,m\leq 10^5,1\leq c\leq n 1≤T≤10,3≤n,m≤105,1≤c≤n
题解
我们可以发现,这个图是一个基环树。
下面先考虑这个图是一棵树的情况。
我们考虑将一条边的修改看成给这条边删去颜色和给这条边加上颜色两个部分,那么一开始加边时处理边的颜色也可以看作给没有颜色的边加上颜色。
我们先考虑删去一条边的颜色对答案的贡献,设这条边的两个端点为 x , y x,y x,y,颜色为 c c c:
- 如果 x x x有另外一条颜色为 c c c的边, y y y也有,则删去这条边后,原本的这个连通块会变成两个连通块,答案加一
- 如果 x x x有另外一条颜色为 c c c的边, y y y没有,则删去这条边后,原本的这个连通块会少一个点 x x x,答案不变
- 如果 x x x没有另外一条颜色为 c c c的边, y y y有,则删去这条边后,原本的这个连通块会少一个点 y y y,答案不变
- 如果 x x x没有另外一条颜色为 c c c的边, y y y也没有,则删去这条边后,这个只由 x x x和 y y y构成的连通块就没了,答案减一
再考虑加上一条边的颜色对答案的贡献,设这条边的两个端点为 x , y x,y x,y,颜色为 c c c:
- 如果 x x x有另外一条颜色为 c c c的边, y y y也有,则加上这条边后,原本的这两个连通块会变成一个连通块,答案减一
- 如果 x x x有另外一条颜色为 c c c的边, y y y没有,则加上这条边后,原本的这个连通块会多一个点 y y y,答案不变
- 如果 x x x没有另外一条颜色为 c c c的边, y y y有,则加上这条边后,原本的这个连通块会多一个点 x x x,答案不变
- 如果 x x x没有另外一条颜色为 c c c的边, y y y也没有,则加上这条边后,就会构成一个只由 x x x和 y y y构成的连通块,答案加一
而当这个图是基环树的时候,有一些特殊情况需要特判:
- 如果边在环上,且环上的边的颜色都是 c c c,则删去这条边后答案不变
- 如果边在环上,且环上除了这条边之外的边的颜色都是 c c c,则加上这条边后答案不变
我们先找出环,然后按上面说的做就可以了。
注意在查找两个端点为 x , y x,y x,y的边的编号和每个点是否有每种颜色的边的时候,可以用 m a p map map来储存。
时间复杂度为 O ( n log n ) O(n\log n) O(nlogn)。
code
#include<bits/stdc++.h>
using namespace std;
const int N=100000;
int T,n,m,tot,d[2*N+5],l[2*N+5],r[N+5],c[N+5];
int ans,top,st[N+5],lp[N+5],dep[N+5],z[N+5],sum[N+5];
map<int,int>mp[N+5],hv[N+5];
struct node{int x,y,v;
}w[N+5];
void add(int xx,int yy){l[++tot]=r[xx];d[tot]=yy;r[xx]=tot;
}
void dfs(int u,int fa){dep[u]=dep[fa]+1;st[++top]=u;for(int i=r[u];i;i=l[i]){if(d[i]==fa) continue;if(dep[d[i]]&&dep[d[i]]<dep[u]){while(st[top]!=d[i]){lp[++lp[0]]=st[top];--top;}lp[++lp[0]]=d[i];}if(!dep[d[i]]) dfs(d[i],u);}if(st[top]==u) --top;
}
void pt(int x,int y,int v,int zt){int tmp=(hv[x][v]!=0)+(hv[y][v]!=0);++hv[x][v];++hv[y][v];if(zt) ++sum[v];if(zt&&sum[v]==lp[0]) --tmp;ans+=1-tmp;
}
void del(int x,int y,int v,int zt){--hv[x][v];--hv[y][v];int tmp=(hv[x][v]!=0)+(hv[y][v]!=0);if(zt&&sum[v]==lp[0]) --tmp;if(zt) --sum[v];ans-=1-tmp;
}
int main()
{freopen("tour.in","r",stdin);freopen("tour.out","w",stdout);scanf("%d",&T);while(T--){scanf("%d%d",&n,&m);tot=0;ans=0;for(int i=0;i<=N;i++){r[i]=dep[i]=z[i]=c[i]=sum[i]=0;mp[i].clear();hv[i].clear();}for(int i=1,x,y,v;i<=n;i++){scanf("%d%d%d",&x,&y,&v);w[i]=(node){x,y,v};add(x,y);add(y,x);mp[x][y]=mp[y][x]=i;}top=0;lp[0]=0;dfs(1,0);for(int i=1,x,y;i<=lp[0];i++){x=lp[i];y=lp[i%lp[0]+1];z[mp[x][y]]=1;}for(int i=1;i<=n;i++){pt(w[i].x,w[i].y,w[i].v,z[i]);c[i]=w[i].v;}for(int i=1,x,y,v,p;i<=m;i++){scanf("%d%d%d",&x,&y,&v);p=mp[x][y];del(x,y,c[p],z[p]);pt(x,y,v,z[p]);c[p]=v;printf("%d\n",ans);}}return 0;
}
相关文章:

NOIP2023模拟6联测27 旅行
题目大意 有一个有 n n n个点 n n n条边的无向连通图,一开始每条边都有一个颜色 c c c。 有 m m m次操作,每次操作将一条两个端点为 x , y x,y x,y的边的颜色修改为 c c c。求每次修改之后,图中有多少个颜色相同的连通块。 一个颜色相同的…...
【表面缺陷检测】钢轨表面缺陷检测数据集介绍(2类,含xml标签文件)
一、介绍 钢轨表面缺陷检测是指通过使用各种技术手段和设备,对钢轨表面进行检查和测量,以确定是否存在裂纹、掉块、剥离、锈蚀等缺陷的过程。这些缺陷可能会对铁路运输的安全和稳定性产生影响,因此及时进行检测和修复非常重要。钢轨表面缺陷…...
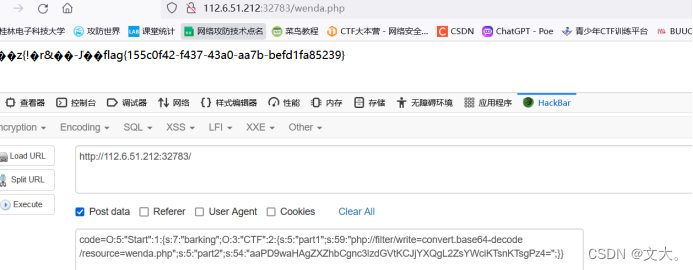
SHCTF 2023 新生赛 Web 题解
Web [WEEK1]babyRCE 源码过滤了cat 空格 我们使用${IFS}替换空格 和转义获得flag [WEEK1]飞机大战 源码js发现unicode编码 \u005a\u006d\u0078\u0068\u005a\u0033\u0074\u006a\u0059\u006a\u0045\u007a\u004d\u007a\u0067\u0030\u005a\u0069\u0030\u0031\u0059\u006d\u0045…...
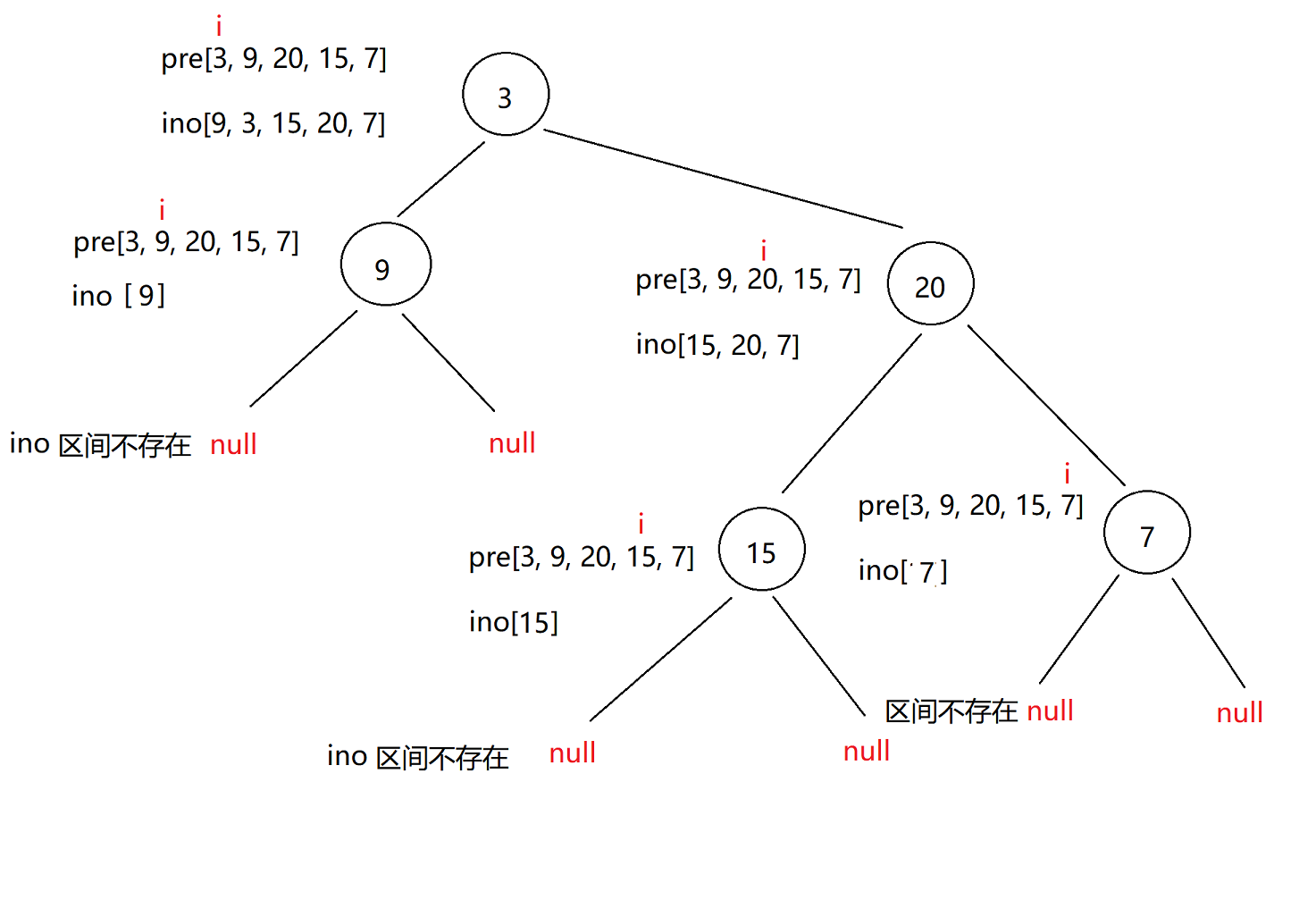
二叉树题目合集(C++)
二叉树题目合集 1.二叉树创建字符串(简单)2.二叉树的分层遍历(中等)3.二叉树的最近公共祖先(中等)4.二叉树搜索树转换成排序双向链表(中等)5.根据树的前序遍历与中序遍历构造二叉树&…...
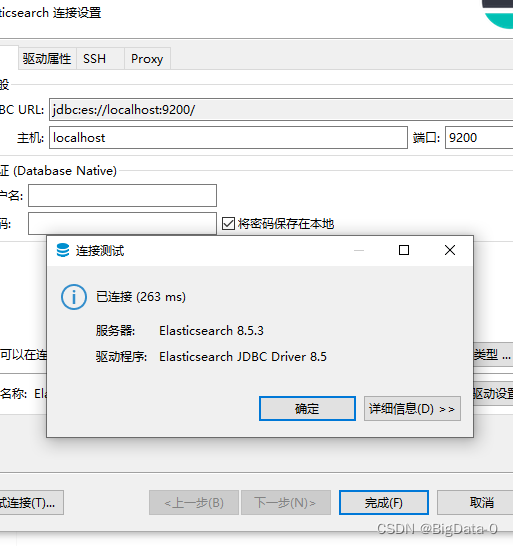
dbeaver配置es连接org.elasticsearch.xpack.sql.jdbc.EsDriver
查看目标es服务版本,下载对应驱动...

有监督学习线性回归
1、目标分析(回归问题还是分类问题?) 2、获取、处理数据 3、创建线性回归模型 4、训练模型 5、模型测试 x_data [[6000, 58], [9000, 77], [11000, 89], [15000, 54]] # 样本特征数据 y_data [30000, 55010, 73542, 63201] # 样本目标数…...
如何在vscode中添加less插件
Less (Leaner Style Sheets 的缩写) 是一门向后兼容的 CSS 扩展语言。它对CSS 语言增加了少许方便的扩展,通过less可以编写更少的代码实现更强大的样式。但less不是css,浏览器不能直接识别,即浏览器无法执行less代码&a…...
mediapipe 训练自有图像数据分类
参考: https://developers.google.com/mediapipe/solutions/customization/image_classifier https://colab.research.google.com/github/googlesamples/mediapipe/blob/main/examples/customization/image_classifier.ipynb#scrollToplvO-YmcQn5g 安装:…...
函数)
【pytorch】torch.gather()函数
dim0时 index[ [x1,x2,x2],[y1,y2,y2],[z1,z2,z3] ]如果dim0 填入方式为: index[ [(x1,0),(x2,1),(x3,2)][(y1,0),(y2,1),(y3,2)][(z1,0),(z2,1),(z3,2)] ]input [[1, 2, 3, 4],[5, 6, 7, 8],[9, 10, 11, 12] ] # shape(3,4) input torch.…...

Mac 安装psycopg2,报错Error: pg_config executable not found.
在mac 上安装psycopg2的方法:执行:pip3 install psycopg2-binary。 如果执行pip3 install psycopg2,无法安装psycopg2 报错信息如下: Collecting psycopg2Using cached psycopg2-2.9.9.tar.gz (384 kB)Preparing metadata (set…...

域名系统 DNS
DNS 概述 域名系统 DNS(Domain Name System)是因特网使用的命名系统,用来把便于人们使用的机器名字转换成为 IP 地址。域名系统其实就是名字系统。为什么不叫“名字”而叫“域名”呢?这是因为在这种因特网的命名系统中使用了许多的“域(domain)”&#x…...

Vue $nextTick 模板解析后在执行的函数
this.$nextTick(()>{ 模板解析后在执行的函数 })...

VBA技术资料MF76:将自定义颜色添加到调色板
我给VBA的定义:VBA是个人小型自动化处理的有效工具。利用好了,可以大大提高自己的工作效率,而且可以提高数据的准确度。我的教程一共九套,分为初级、中级、高级三大部分。是对VBA的系统讲解,从简单的入门,到…...

zilong-20231030
1)k个反转 2)n!转12进制 求末尾多少0 一共有几位 (考虑了溢出问题) 3)大量数据获取前10个 4)reemap地城结构 5)红黑树规则特性 6)热更 7)压测 8)业务 跨服实现 9)有哪些线程以及怎么分配...
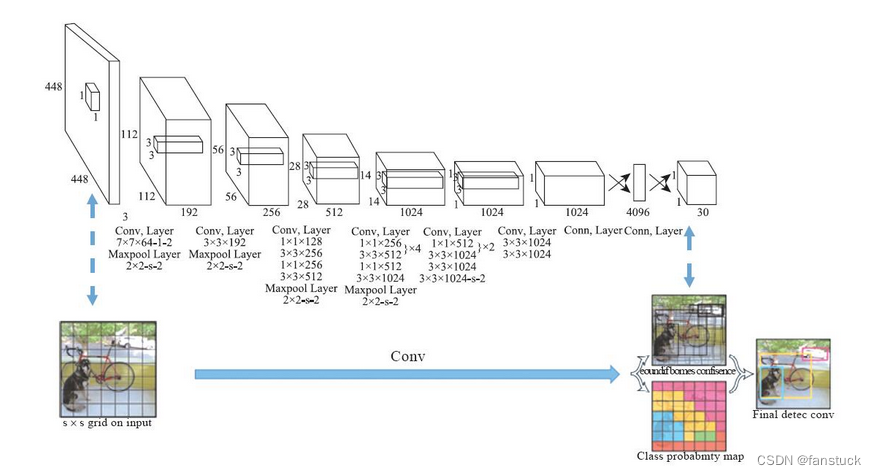
目标检测算法发展史
前言 比起图像识别,现在图片生成技术要更加具有吸引力,但是要步入AIGC技术领域,首先不推荐一上来就接触那些已经成熟闭源的包装好了再提供给你的接口网站,会使用别人的模型生成一些图片就能叫自己会AIGC了吗?那样真正…...
React 生成传递给无障碍属性的唯一 ID
useId() 在组件的顶层调用 useId 生成唯一 ID: import { useId } from react; function PasswordField() { const passwordHintId useId(); // ...参数 useId 不带任何参数。 返回值 useId 返回一个唯一的字符串 ID,与此特定组件中的 useI…...
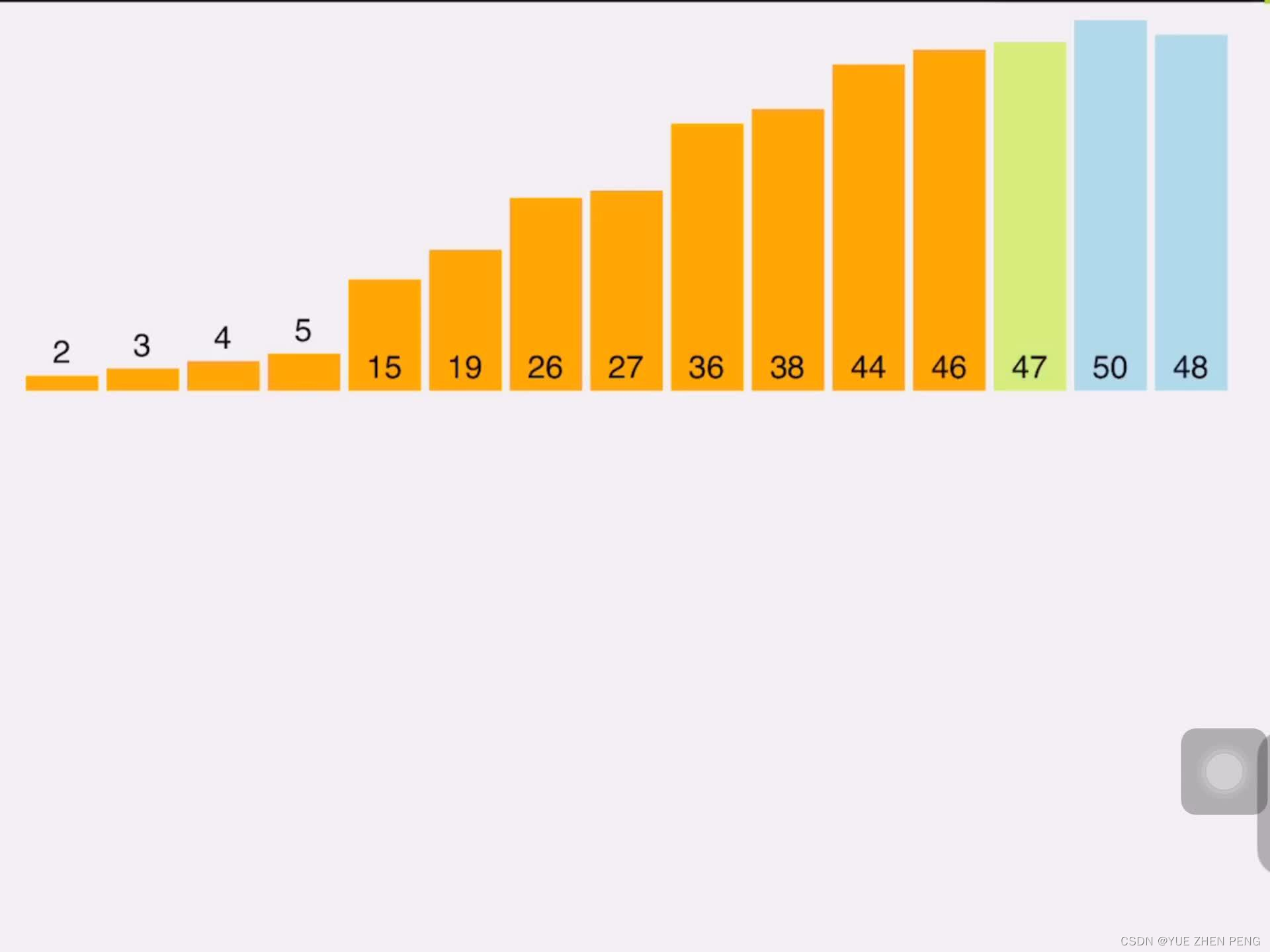
十种排序算法(1) - 准备测试函数和工具
1.准备工作 我们先写一堆工具,后续要用,不然这些写在代码里可读性巨差 #pragma once #include<stdio.h>//为C语言定义bool类型 typedef int bool; #define false 0 #define true 1//用于交互a和b inline void swap(int* a, int* b) {/*int c *a…...

IRF联动 BFD-MAD
文章目录 IRF堆叠一、主设备配置二、备设备配置三、验证 MAD检测一、MAD检测二、MAD验证 本实验以2台设备进行堆叠示例,按照配置顺序,先配置主设备,再配置备设备。在IRF配置前暂时先不接堆叠线,按步骤提示接线。 IRF堆叠 一、主设…...
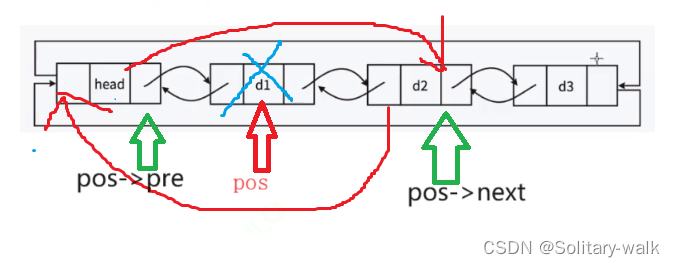
双向链表的初步练习
𝙉𝙞𝙘𝙚!!👏🏻‧✧̣̥̇‧✦👏🏻‧✧̣̥̇‧✦ 👏🏻‧✧̣̥̇: Solitary-walk ⸝⋆ ━━━┓ - 个性标签 - :来于“云”的“羽球人”…...
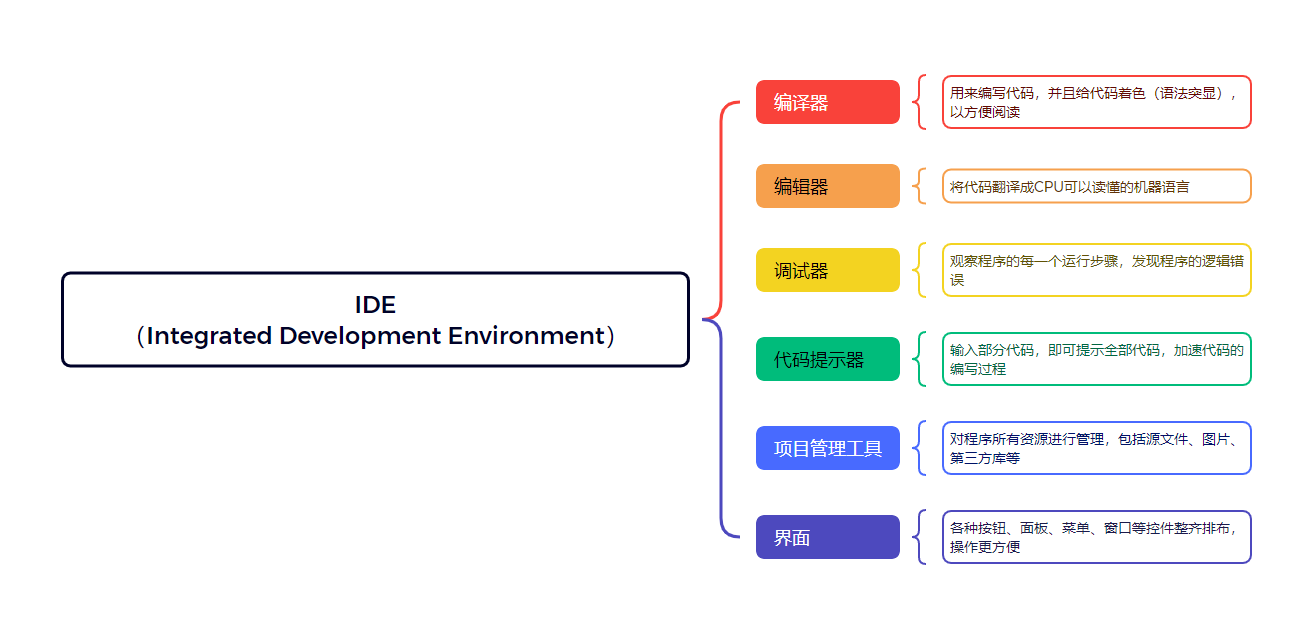
IDE的组成
集成开发环境(IDE,Integrated Development Environment )是用于提供程序开发环境的应用程序,一般包括代码编辑器、编译器、调试器和图形用户界面等工具。集成了代码编写功能、分析功能、编译功能、调试功能等一体化的开发软件服务…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...

django blank 与 null的区别
1.blank blank控制表单验证时是否允许字段为空 2.null null控制数据库层面是否为空 但是,要注意以下几点: Django的表单验证与null无关:null参数控制的是数据库层面字段是否可以为NULL,而blank参数控制的是Django表单验证时字…...

从物理机到云原生:全面解析计算虚拟化技术的演进与应用
前言:我的虚拟化技术探索之旅 我最早接触"虚拟机"的概念是从Java开始的——JVM(Java Virtual Machine)让"一次编写,到处运行"成为可能。这个软件层面的虚拟化让我着迷,但直到后来接触VMware和Doc…...

第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10+pip3.10)
第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10pip3.10) 一:前言二:安装编译依赖二:安装Python3.10三:安装PIP3.10四:安装Paddlepaddle基础框架4.1…...
:LeetCode 142. 环形链表 II(Linked List Cycle II)详解)
Java详解LeetCode 热题 100(26):LeetCode 142. 环形链表 II(Linked List Cycle II)详解
文章目录 1. 题目描述1.1 链表节点定义 2. 理解题目2.1 问题可视化2.2 核心挑战 3. 解法一:HashSet 标记访问法3.1 算法思路3.2 Java代码实现3.3 详细执行过程演示3.4 执行结果示例3.5 复杂度分析3.6 优缺点分析 4. 解法二:Floyd 快慢指针法(…...

大数据驱动企业决策智能化的路径与实践
📝个人主页🌹:慌ZHANG-CSDN博客 🌹🌹期待您的关注 🌹🌹 一、引言:数据驱动的企业竞争力重构 在这个瞬息万变的商业时代,“快者胜”的竞争逻辑愈发明显。企业如何在复杂环…...

用鸿蒙HarmonyOS5实现国际象棋小游戏的过程
下面是一个基于鸿蒙OS (HarmonyOS) 的国际象棋小游戏的完整实现代码,使用Java语言和鸿蒙的Ability框架。 1. 项目结构 /src/main/java/com/example/chess/├── MainAbilitySlice.java // 主界面逻辑├── ChessView.java // 游戏视图和逻辑├── …...
