当前位置： 首页 > news >正文

百度网站开发/百度免费seo

news 文章来源：https://blog.csdn.net/weixin_44529258/article/details/134065694 2025/3/10 15:12:39
百度网站开发,百度免费seo,asp.net构建门户网站,绿色系的网站ID3算法 假定当前样本集合D中第k类样本所占比例为pk，则样本集合D的信息熵定义为 信息增益 C4.5算法 ID3算法存在一个问题，就是偏向于取值数目较多的属性，因此C4.5算法使用了“增益率”（gain ratio）来选择划分属性 CA…

ID3算法

假定当前样本集合D中第k类样本所占比例为pk，则样本集合D的信息熵定义为

信息增益

C4.5算法

ID3算法存在一个问题，就是偏向于取值数目较多的属性，因此C4.5算法使用了“增益率”（gain ratio）来选择划分属性

CART算法

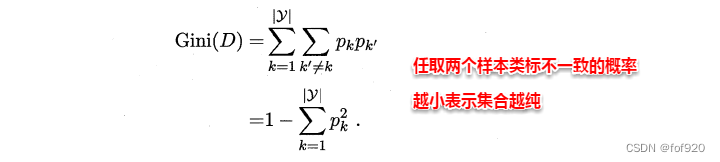
使用属性α划分后的基尼指数为

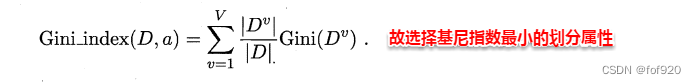
剪枝处理

* 预剪枝（prepruning）：在构造的过程中先评估，再考虑是否分支。  
* 后剪枝（post-pruning）：在构造好一颗完整的决策树后，自底向上，评估分支的必要性。

评估指的是性能度量，即决策树的泛化性能。 

连续值与缺失值处理

连续值

* 首先将α的所有取值按升序排列，所有相邻属性的均值作为候选划分点（n-1个，n为α所有的取值数目）。  
* 计算每一个划分点划分集合D（即划分为两个分支）后的信息增益。  
* 选择最大信息增益的划分点作为最优划分点。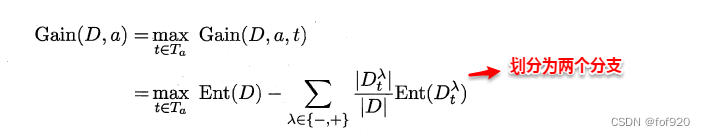

缺失值

假定为样本集中的每一个样本都赋予一个权重，根节点中的权重初始化为1，则定义：

通过在样本集D中选取在属性α上没有缺失值的样本子集，计算在该样本子集上的信息增益，最终的信息增益等于该样本子集划分后信息增益乘以样本子集占样本集的比重。即：

对于（2）：若该样本子集在属性α上的值缺失，则将该样本以不同的权重（即每个分支所含样本比例）划入到所有分支节点中。该样本在分支节点中的权重变为：

多变量决策树

对于高维数据空间，决策树形成的分类边界有一个特点：轴平行，引入多变量决策树实现斜划分，分裂节点变为k1*x1+k2*x2+...

相关文章：

吃瓜教程3|决策树

ID3算法 假定当前样本集合D中第k类样本所占比例为pk，则样本集合D的信息熵定义为 信息增益 C4.5算法 ID3算法存在一个问题，就是偏向于取值数目较多的属性，因此C4.5算法使用了“增益率”（gain ratio）来选择划分属性 CA…...

编程日记 2023/10/30 21:29:29

springboot动态数据源【非伪数据源】

说明&#xff1a;本文章的数据源不是在配置文件中配置两个或多个数据源&#xff0c;在业务方面对这些数据源来回切换&#xff0c;本文章中的数据源是可以动态添加&#xff0c;修改&#xff0c;切换的&#xff0c;废话不多说。 先看工程图&#xff1a; 1.pom.xml文件 <?x…...

编程日记 2023/10/30 21:27:25

如何改善设备综合效率（OEE）并提高工厂的生产力

在现代制造业中&#xff0c;提高设备综合效率&#xff08;Overall Equipment Efficiency&#xff0c;OEE&#xff09;是企业追求高效生产和优化生产能力的重要目标之一。OEE是一个关键的绩效指标&#xff0c;可以帮助企业评估设备的利用效率、生产效率和质量水平。本文将从三个…...

编程日记 2023/10/30 21:26:24

一文接入Android阿里Sophix热更新

最近公司项目渐趋成熟&#xff0c;已经不需要经常更新版本&#xff0c;并且更新版本对客户的影响特别大&#xff0c;但是日常维护难免需要更新代码&#xff0c;因此热修复的技术&#xff0c;就比较迫切了。 经过一段时间的对比&#xff0c;我们最终决定使用阿里的Sophix方案&am…...

编程日记 2023/10/30 21:25:23

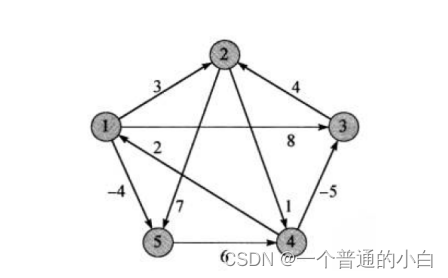
【高阶数据结构】并查集和图

目录 1.数据结构--并查集 2.数据结构--图 1.图的基础概念 2.图的简单实现 2.1.邻接矩阵的图实现 2.2.邻接表的图实现 2.3.图的DFS和BFS 2.4.最小生成树 2.4.1.Kruskal(克鲁斯卡尔算法) 2.4.2.Prim&#xff08;普里姆算法&#xff09; 2.5.最短路径 2.5.1.Dijkstra(…...

编程日记 2023/10/30 21:24:22

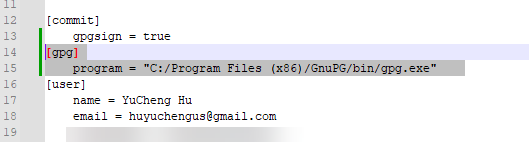
Git 提交时提示 GPG 签名错误

本来应该一切都是正常的&#xff0c;但今天提交的时候提示 GPG 签名错误。 错误的信息就是 GPG 签名失败。 gpg: skipped "942395299055675C": No secret key gpg: signing failed: No secret key error: gpg failed to sign the data fatal: failed to write commi…...

编程日记 2023/10/30 21:22:18

vite+vue3实现 tomcat 的本地部署

背景&#xff1a; 很多开发小伙伴在本地开发完前端项目后&#xff0c;碍于服务端环境配置麻烦&#xff0c;想先试试在本地部署&#xff0c;已开发好的前端项目&#xff0c;由于很多文章都是文字性描述&#xff0c;不太直观&#xff0c;为了给大多数新手提供一个教程&#xff0c…...

编程日记 2023/10/30 21:21:18

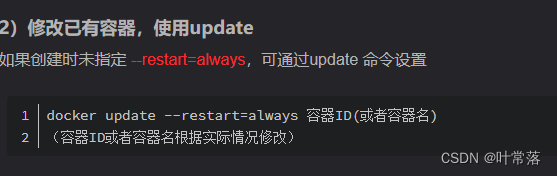
docker+playwright

windows10 docker playwright 难点在于windows下docker的安装&#xff0c;以及官方hub被墙的困难。 wsl2 wsl2 ubuntu docker git clone https://gitee.com/lineuman/lcs_playwright.git npm install npx playwright test docker端口怎么映射到主机上面&#xff1f; 设置重…...

编程日记 2023/10/30 21:20:16

php框架路由实现

在PHP中也有很多框架&#xff08;如Laravel、CodeIgniter&#xff09;提供了路由功能。下面是一个简单的PHP路由实现原理和示例代码&#xff1a; 路由实现原理&#xff1a; 客户端发起请求&#xff0c;请求的URL会被传递给Web服务器。Web服务器将请求传递给PHP解释器&#xff…...

编程日记 2023/10/30 21:18:15

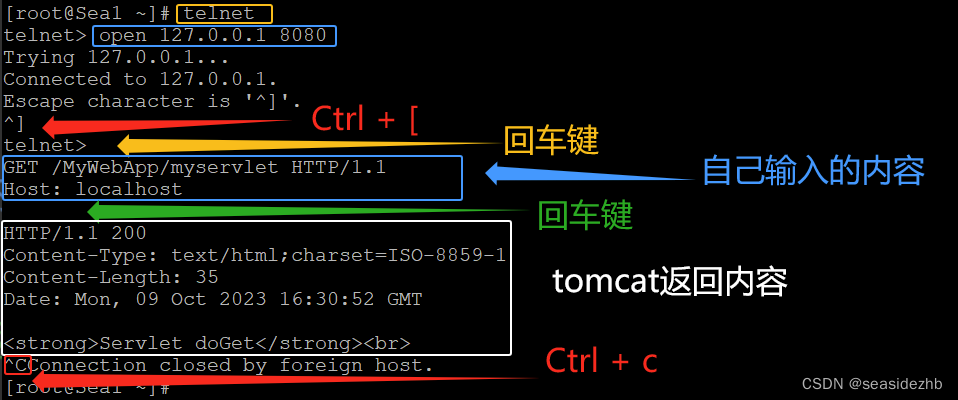
在CentOS 7中手工打造和运行xml文件配置的Servlet，然后使用curl、浏览器、telnet等三种工具各自测试

下载Openjdk并配置环境变量 https://jdk.java.net/java-se-ri/11-MR2是官网下载Openjdk 11的地方。 sudo wget https://download.java.net/openjdk/jdk11.0.0.1/ri/openjdk-11.0.0.1_linux-x64_bin.tar.gz下载openjdk 11。 sudo mkdir -p /usr/openjdk11创建目录&#xff…...

编程日记 2023/10/30 21:17:14

单例模式.

目录 ♫什么是单例模式 ♫饿汉式单例模式 ♫懒汉式单例模式 ♫单例模式的线程安全问题 ♪原子性 ♪内存可见性与指令重排序 ♫什么是单例模式 单例模式是一种设计模式&#xff0c;通过巧用Java的现有语法&#xff0c;实现一个只能被创建一个实例的类&#xff0c;并提供一个全…...

编程日记 2023/10/30 21:16:13

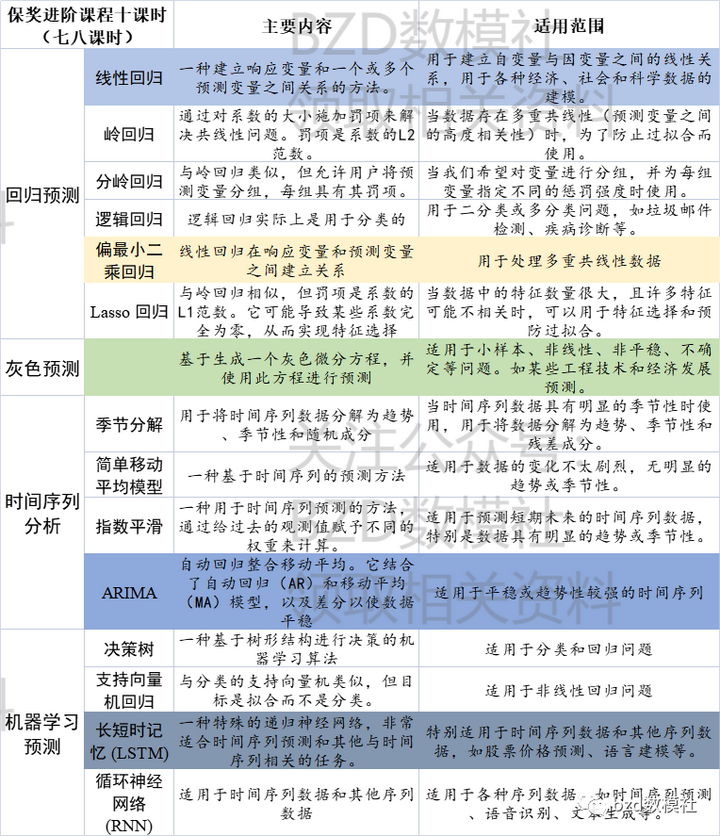
2023年MathorCup高校数学建模挑战赛大数据挑战赛赛题浅析

比赛时长为期7天的妈杯大数据挑战赛如期开赛&#xff0c;为了帮助大家更好的选题&#xff0c;首先给大家带来赛题浅析&#xff0c;为了方便大家更好的选题。 赛道 A&#xff1a;基于计算机视觉的坑洼道路检测和识别 A题&#xff0c;图像处理类题目。这种题目的难度数模独一档…...

编程日记 2023/10/30 21:14:11

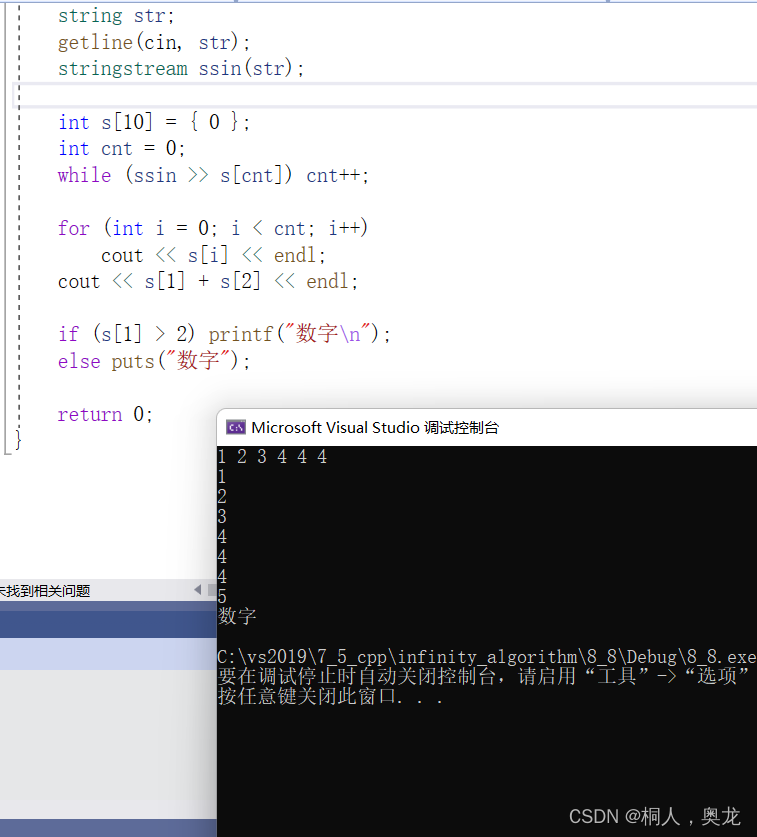
c++小惊喜——stringstream

当需要读取一行字符串时&#xff0c;我们通常会有将这个字符串分开的想法 #include<iostream> #include<sstream> using namespace std;int main() {string str;getline(cin, str);stringstream ssin(str);string s[10];int cnt 0;while (ssin >> s[cnt]) …...

编程日记 2023/10/30 21:12:08

ubuntu 18.04 编译安装flexpart 10.4（2023年） —— 筑梦之路

2023年10月29日 环境说明 操作系统版本&#xff1a;ubuntu 18.04 python版本&#xff1a;3.6.9 gcc版本&#xff1a;7.5.0 编译安装路径&#xff1a;/usr/local cmake: 3.10.2 所需要的源码包我已经打包放到我的资源。 2021年1月份已经写过一篇Ubuntu 编译安装的帖子F…...

编程日记 2023/10/30 21:11:07

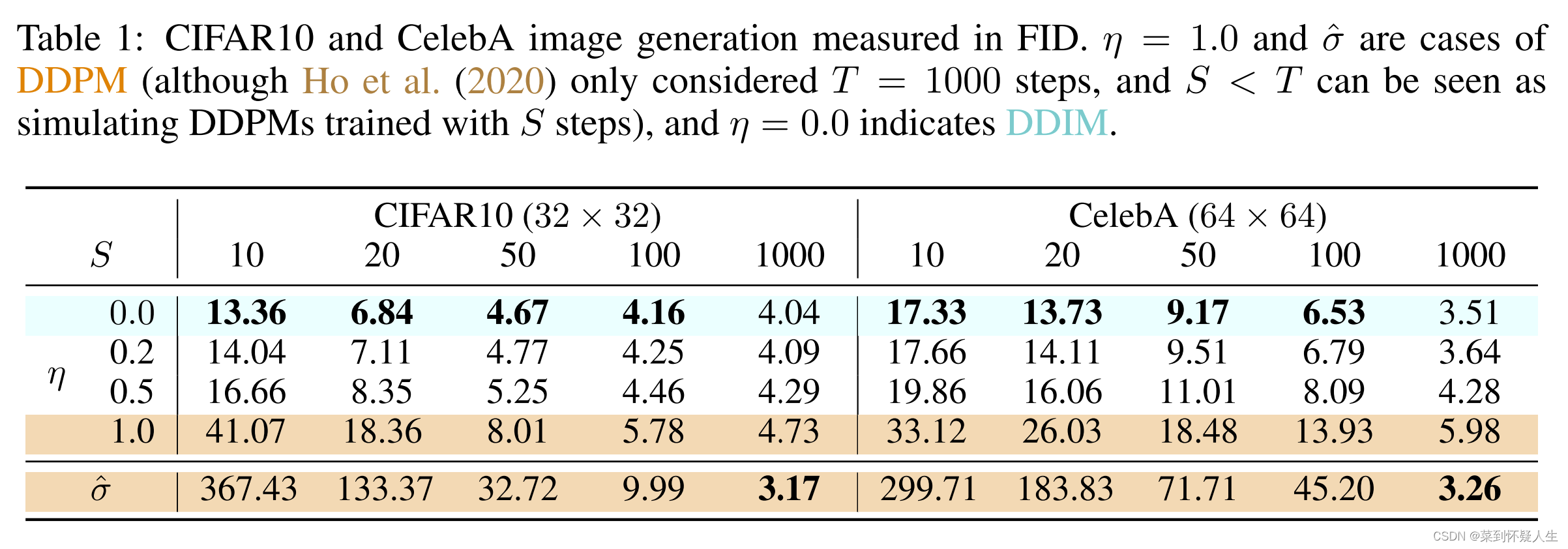
深度学习（生成式模型）——DDIM：Denoising Diffusion Implicit Models

文章目录 前言为什么DDPM的反向过程与前向过程步数绑定DDIM如何减少DDPM反向过程步数DDIM的优化目标DDIM的训练与测试 前言 上一篇博文介绍了DDIM的前身DDPM。DDPM的反向过程与前向过程步数一一对应&#xff0c;例如前向过程有1000步&#xff0c;那么反向过程也需要有1000步&a…...

编程日记 2023/10/30 21:10:05

HashMap的遍历方式 -- 好几次差点记不起来总结了一下

public class HashMapDemo {public static void main(String[] args) {// 创建一个HashMap并添加一些键值对Map<String, Integer> hashMap new HashMap<>();hashMap.put("Alice", 25);hashMap.put("Bob", 30);hashMap.put("Charlie"…...

编程日记 2023/10/30 21:09:04

PostgreSQL 两表关联更新sql

PostgreSQL两表关联更新SQL如下&#xff1a; UPDATE user SET username ft.name, age ft.age FROM userinfo WHERE user.id ft.id; user 要更新的表 userinfo数据来源表...

编程日记 2023/10/30 21:08:03

R2R 的一些小tip

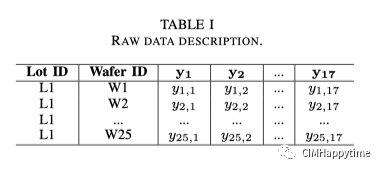
批次间控制器(Run-to-run Controller)&#xff0c;以应对高混合生产的挑战。将最优配方参数与各种工业特征相关联的模型是根据历史数据离线训练的。预测的最优配方参数在线用于调整工艺条件。 批次控制(R2R control)是一种先进的工艺控制技术&#xff0c;可在运行(如批次或晶圆…...

编程日记 2023/10/30 21:07:01

UML中类之间的六种主要关系

UML中类之间的六种主要关系: 继承&#xff08;泛化&#xff09;&#xff08;Inheritance、Generalization&#xff09;, 实现&#xff08;Realization&#xff09;&#xff0c;关联&#xff08;Association)&#xff0c;聚合&#xff08;Aggregation&#xff09;&#xff0c;组…...

编程日记 2023/10/30 21:06:00

机器学习-朴素贝叶斯之多项式模型

多项式模型&#xff1a; 记住一定用于离散的对象&#xff0c;不能是连续的 于高斯分布相反&#xff0c;多项式模型主要适用于离散特征的概率计算&#xff0c;切sklearn的多项式模型不接受输入负值 因为多项式不接受负值的输入&#xff0c;所以样本数据的特征为数值型数据&…...

编程日记 2023/10/30 21:05:00

下载的nginx证书转换成tomcat证书格式

1、下载的nginx证书格式 XXX.crt private.key 2、转换成JKS格式证书步骤 #crt格式证书转pem openssl x509 -in xxx.crt -out xxx.pem#先转成p12格式&#xff0c;此时注意&#xff0c;如果有别名&#xff0c;需要设置 openssl pkcs12 -export -in xxx.crt -inkey private.key…...

编程日记 2023/10/30 21:03:58

计算机毕业设计选题推荐-社区志愿者服务微信小程序/安卓APP-项目实战

✨作者主页&#xff1a;IT毕设梦工厂✨ 个人简介&#xff1a;曾从事计算机专业培训教学&#xff0c;擅长Java、Python、微信小程序、Golang、安卓Android等项目实战。接项目定制开发、代码讲解、答辩教学、文档编写、降重等。 ☑文末获取源码☑ 精彩专栏推荐⬇⬇⬇ Java项目 Py…...

编程日记 2023/10/30 21:01:56

ES6中数值扩展

目录 二进制和八进制表示法 Number.isFinite() Number.isNaN() Number.parseInt()和Number.parseFloat() Number.isInteger() Math.trunc() Math.sign() Math.cbrt()&#xff1a; Math.clz32()&#xff1a; Math.imul()&#xff1a; Math.fround()&#xff1a; ES6中…...

编程日记 2023/10/30 20:59:52

sql-50练习题11-15

sql-50练习题11-15 前言数据库表结构介绍学生表课程表成绩表教师表 1-1 查询没有学全所有课程的同学的信息1-2 查询至少有一门课与学号为01的同学所学相同的同学的信息1-3 查询和1号的同学学习的课程完全相同的其他同学的信息1-4 查询没学过张三老师讲授的任一门课程的学生姓名…...

编程日记 2023/10/30 20:57:49

【多线程面试题十九】、 公平锁与非公平锁是怎么实现的？

文章底部有个人公众号&#xff1a;热爱技术的小郑。主要分享开发知识、学习资料、毕业设计指导等。有兴趣的可以关注一下。为何分享&#xff1f; 踩过的坑没必要让别人在再踩&#xff0c;自己复盘也能加深记忆。利己利人、所谓双赢。 面试官&#xff1a; 公平锁与非公平锁是怎么…...

编程日记 2023/10/30 20:55:47

3.4每日一题（变量可分离方程通解）

...

编程日记 2023/10/30 20:53:45

LabVIEW背景颜色设为和其他程序或图像中一样

LabVIEW背景颜色设为和其他程序或图像中一样 有时候LabVIEW背景色要和其他程序或者图片的颜色保持一致&#xff0c;如果要求不高可以大致设置一下。如果要求较高&#xff0c;那可以按照如下的方式。 先用PS打开标准图像&#xff0c;之后用吸管工具选择图像上中的点&#xff0…...

编程日记 2023/10/30 20:52:43

图表参考线，数据对比一目了然_三叠云

参考线 路径 仪表盘 >> 仪表盘设计 功能简介 新增「参考线」功能。 参考线是在单个图表组件中添加的一条水平虚线&#xff0c;也可以配置两条线形成的参考区间&#xff0c;它表示该水平线上纵坐标值的大小。 使用场景&#xff1a; 通过辅助线的设置&#xff0c;可…...

编程日记 2023/10/30 20:51:43

【深度学习】Transformer、GPT、BERT、Seq2Seq什么区别？

请看vcr&#xff1a;https://transformers.run/back/transformer/...

编程日记 2023/10/30 20:50:41

数据结构与算法之LRU: 实现 LRU 缓存算法功能 (Javascript版)

关于LRU缓存 LRU - Lease Recently Used 最近使用 如果内存优先&#xff0c;只缓存最近使用的&#xff0c;删除 ‘沉睡’ 数据 核心 api: get set 分析 使用哈希表来实现, O(1)必须是有序的&#xff0c;常用放在前面&#xff0c;沉睡放在后面, 即&#xff1a;有序&#xff0…...

编程日记 2023/10/30 20:49:39