基于纵横交叉算法的无人机航迹规划-附代码
基于纵横交叉算法的无人机航迹规划
文章目录
- 基于纵横交叉算法的无人机航迹规划
- 1.纵横交叉搜索算法
- 2.无人机飞行环境建模
- 3.无人机航迹规划建模
- 4.实验结果
- 4.1地图创建
- 4.2 航迹规划
- 5.参考文献
- 6.Matlab代码
摘要:本文主要介绍利用纵横交叉算法来优化无人机航迹规划。
1.纵横交叉搜索算法
纵横交叉算法原理请参考:https://blog.csdn.net/u011835903/article/details/109514424
2.无人机飞行环境建模
? 环境模型的建立是考验无人机是否可以圆满完成人类所赋予各项任务的基
础和前提,其中第一步便是如何描述规划空间中的障碍物。首先我们将采取函数模拟法模拟地貌特征。其函数表达式为:
z ( x , y ) = s i n ( y + a ) + b s i n ( x ) + c c o s ( d y 2 + x 2 ) + e c o s ( y ) + f s i n ( f y 2 + x 2 ) + g c o s ( y ) (1) z(x,y)=sin(y+a)+bsin(x)+ccos(d\sqrt{y^2+x^2})+ecos(y)+fsin(f\sqrt{y^2+x^2})+gcos(y)\tag{1} z(x,y)=sin(y+a)+bsin(x)+ccos(dy2+x2)+ecos(y)+fsin(fy2+x2)+gcos(y)(1)
其中, ( x , y ) (x, y) (x,y) 为地形上某点投影在水平面上的点坐标, z z z 则为对应点坐标的高度。式中 a , b , c , d , e , f , g a, b, c, d, e, f , g a,b,c,d,e,f,g 是常系数,想要得到不同的地貌特征可以通过改变其常系数的大小,以上建模是作为环境模型的基准地形信息。但为了得到障碍区域我们还需要在这个基准地形上叠加山峰模型,这样就可以模拟像山峰、丘陵等障碍地理信息。山峰模型的数学表达式为:
h ( x , y ) = ∑ i h i e x p [ − ( x − x o i ) 2 a i 2 − ( y − y o i ) 2 b i 2 ] + h o (2) h(x,y)=\sum_ih_iexp[-\frac{(x-x_{oi})^2}{a_i^2}-\frac{(y-y_{oi})^2}{b_i^2}]+h_o \tag{2} h(x,y)=i∑hiexp[−ai2(x−xoi)2−bi2(y−yoi)2]+ho(2)
式 (2)中, h o h_o ho 和 h i h_i hi 分别表示基准地形和第 i i i座山峰的高度, ( x o i , y o i ) (xoi , y oi ) (xoi,yoi)则表示第 i座山峰的中心坐标位置,a i 和 b i 分别是第 i 座山峰沿 x 轴和 y 轴方向的坡度。由式(1)和(2),我们可以得到如下表达式:
Z ( x , y ) = m a x [ z ( x , y ) , h ( x , y ) ] (3) Z(x,y)=max[z(x,y),h(x,y)]\tag{3} Z(x,y)=max[z(x,y),h(x,y)](3)
无人机在躲避障碍物的同时也会经常遇到具有威胁飞行安全的区域,我们称之为威胁区域。这些威胁区域可以是敌人的雷达和防空导弹系统的探测威胁区域也可以是一些其它的威胁,一旦无人机进入这些区域很有可能会被击落或者坠毁。为了简化模型,本文采用半径为 r 的圆柱形区域表示威胁区域,其半径的大小决定威胁区域的覆盖范围。每一个圆柱体的中心位置是对无人机构成最大威胁的地方并向外依次减弱。
3.无人机航迹规划建模
? 在环境建模的基础上,无人机航迹规划需要考虑到在执行复杂任务的过程中自身性能约束要求,合理的设计航迹评价函数才能使得纵横交叉搜索算法得出的最后结果符合要求,并保证规划出的航迹是有效的。考虑到实际环境中,无人机需要不断适应变化的环境。所以在无人机路径规划过程中,最优路径会显得比较复杂,并包含许多不同的特征。基于实际的情况,本文采用较为复杂的航迹评价函数进行无人机路径规划。影响无人机性能的指标主要包括航迹长度、飞行高度、最小步长、转角代价、最大爬升角等。
? 搜索最佳路径通常与搜索最短路径是密不可分的。在无人机航迹规划过程中,航迹的长度对于大多数航迹规划任务来说也是非常重要的。众所周知,较短的路线可以节省更多的燃料和更多的时间并且发现未知威胁的几率会更低。我们一般把路径定义为无人机从起始点到终点所飞行路程的值,设一条完整的航线有 n n n个节点,其中第 i i i个航路点和第 i + 1 i+1 i+1个航路点之间的距离表示为 l i l_i li ,这两个航路点的坐标分别表示为 ( x i , y i , z i ) (x_i,y_i,z_i ) (xi,yi,zi), ( x i + 1 , y i + 1 , z i + 1 ) (x_{i+1}, y_{i+1},z_{i+1}) (xi+1,yi+1,zi+1)并分别记作 g ( i ) g(i) g(i)和 g ( i + 1 ) g(i+1) g(i+1)。航迹需要满足如下条件:
{ l i = ∣ ∣ g ( i + 1 ) − g ( i ) ∣ ∣ 2 L p a t h = ∑ i = 1 n − 1 l i (4) \begin{cases} l_i = ||g(i+1)-g(i)||_2\\ L_{path}=\sum_{i=1}^{n-1}l_i \end{cases}\tag{4} {li=∣∣g(i+1)−g(i)∣∣2Lpath=∑i=1n−1li(4)
在飞行的过程中会遇到障碍物或者进入威胁区域,如果无人机无法躲避障碍物或者飞入了威胁区域将面临被击落或坠毁的危险以至于无法到达终点,记为 L p a t h = ∞ L_{path}=\infty Lpath=∞,但是无穷函数在实际问题中很难表示,我们采用惩罚的方式进行处理。一般情况下,为了利用地形覆盖自身位置,无人机应尽可能降低高度这可以帮助自身避免一些未知雷达等威胁。但是太低的飞行高度同样会加大无人机同山体和地面的撞击几率,因此设定稳定的飞行高度是非常重要的。飞行高度不应该有太大的变化,稳定的飞行高度可以减少控制系统的负担,节省更多的燃料 。为了使无人机飞行更加安全,给出的飞行高度模型:
{ h h e i g h t = 1 n ∑ i = 0 n − 1 ( z ( i ) − z ‾ ) 2 z ‾ = 1 n ∑ i = 0 n − 1 z ( i ) (5) \begin{cases} h_{height}=\sqrt{\frac{1}{n}\sum_{i=0}^{n-1}(z(i)-\overline{z})^2}\\ \overline{z}=\frac{1}{n}\sum_{i=0}^{n-1}z(i) \end{cases}\tag{5} {hheight=n1∑i=0n−1(z(i)−z)2z=n1∑i=0n−1z(i)(5)
无人机的可操作性也受到其转角代价函数的限制。,在飞行过程中无人机的转角应不大于其预先设定的最大转角,转角的大小会影响其飞行的稳定性。本文的研究中,设定最大转角为 Φ Φ Φ,当前转角为 θ \theta θ并且 a i a_i ai是第 i i i段航路段向量。
{ c o s θ = a i T a i + 1 ∣ a i ∣ ∣ a i + 1 ∣ J t u r n = ∑ i = 1 n ( c o s ( Φ − c o s θ ) ) (6) \begin{cases} cos\theta =\frac{a_i^Ta_{i+1}}{|a_i||a_{i+1}|}\\ J_{turn}=\sum_{i=1}^n(cos(\Phi-cos\theta)) \end{cases}\tag{6} {cosθ=∣ai∣∣ai+1∣aiTai+1Jturn=∑i=1n(cos(Φ−cosθ))(6)
其中, ∣ a ∣ |a| ∣a∣代表矢量 a a a的长度。
? 通过对以上三个方面建立了无人机航迹规划的代价函数,可以得出本文的航迹评价函数如下:
J c o s t = w 1 L p a t h + w 2 h h e i g h t + w 3 J t u r n (7) J_{cost}=w_1L_{path}+w_2h_{height}+w_3J_{turn} \tag{7} Jcost=w1Lpath+w2hheight+w3Jturn(7)
其中, J c o s t J_{cost} Jcost是总的代价函数,参数 w i w_i wi , i = 1 , 2 , 3 i=1,2,3 i=1,2,3 表示每个代价函数的权值,且满足如下条件:
{ w i ≥ 0 ∑ i = 1 3 w i = 1 (8) \begin{cases} w_i\geq0 \\ \sum_{i=1}^3 w_i=1 \end{cases} \tag{8} {wi≥0∑i=13wi=1(8)
通过对总的代价函数进行有效地处理,我们可以得到由线段组成的航迹。不可否认的是得到的路径往往是仅在理论上可行,但为了实际可飞,有必要对航迹进行平滑处理。本文采用三次样条插值的方法对路径进行平滑。
4.实验结果
4.1地图创建
设置地图参数a, b, c, d, e, f , g=1。地图大小为:200*200。设置三个山峰,山峰信息如表1所示。威胁区域信息如表2所示
| 信息 | 山峰中心坐标 | 山峰高度 | 山峰X方向坡度 | 山峰y方向坡度 |
|---|---|---|---|---|
| 山峰1 | [60,60] | 50 | 20 | 20 |
| 山峰2 | [100,100] | 60 | 30 | 30 |
| 山峰3 | [150,150] | 80 | 20 | 20 |
| 信息 | 威胁区域中心坐标 | 威胁区域半径 |
|---|---|---|
| 威胁区域1 | [150,50] | 30 |
| 威胁区域2 | [50,150] | 20 |
创建的地图如下:

4.2 航迹规划
设置起点坐标为[0,0,20],终点坐标为[200,200,20]。利用纵横交叉算法对航迹评价函数式(7)进行优化。优化结果如下:

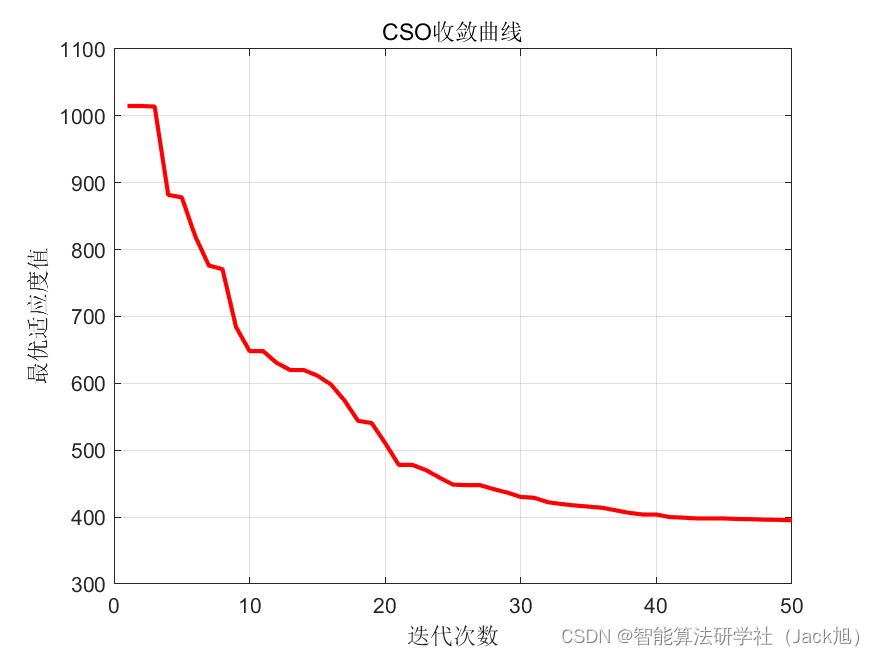
从结果来看,纵横交叉算法规划出了一条比较好的路径,表明算法具有一定的优势。
5.参考文献
[1]薛建凯. 一种新型的群智能优化技术的研究与应用[D].东华大学,2020.DOI:10.27012/d.cnki.gdhuu.2020.000178.
6.Matlab代码
相关文章:

基于纵横交叉算法的无人机航迹规划-附代码
基于纵横交叉算法的无人机航迹规划 文章目录 基于纵横交叉算法的无人机航迹规划1.纵横交叉搜索算法2.无人机飞行环境建模3.无人机航迹规划建模4.实验结果4.1地图创建4.2 航迹规划 5.参考文献6.Matlab代码 摘要:本文主要介绍利用纵横交叉算法来优化无人机航迹规划。 …...

D-Bus:数据类型
D-Bus中描述接口的属性和方法,有其自己定义的一套签名描述方式: 数据类型描述符号对应C++数据类型avector/array数组, ai表示的是vector<int32_t>bboolddouble双精度浮点数iint32_t,32位有符号整数nint16_t,16位有符号整数oobject_path对象路径quint16_t,16位无符号…...

BI零售数据分析,告别拖延症,及时掌握一线信息
在日常的零售数据分析中,经常会因为数据量太大,分析指标太多且计算组合多变而导致数据分析报表难产,零售运营决策被迫拖延症。随着BI数据可视化分析技术的发展,智能化、可视化、自助分析的BI数据分析逐渐成熟,形成一套…...
[BUUCTF NewStarCTF 2023 公开赛道] week4 crypto/pwn
再补完这个就基本上完了. crypto RSA Variation II Schmidt-Samoa密码系统看上去很像RSA,其中Npqq, 给的eN给了d from secret import flag from Crypto.Util.number import *p getPrime(1024) q getPrime(1024)N p*p*qd inverse(N, (p-1)*(q-1)//GCD(p-1, q-1))m bytes…...

论文范文:论基于架构的软件设计方法及应用
注意:范文只适用于帮助大家打开写作思路,并不能作为素材直接用于平时练习、考试中。考试中直接使用范文的素材,会有被认定为雷同卷的风险。 摘要: 2022年4月,本人所在单位计划研发生态集装箱管理控制平台项目。该平台主要用于与现有公司生态集装箱产品做对接,达到远程控制…...
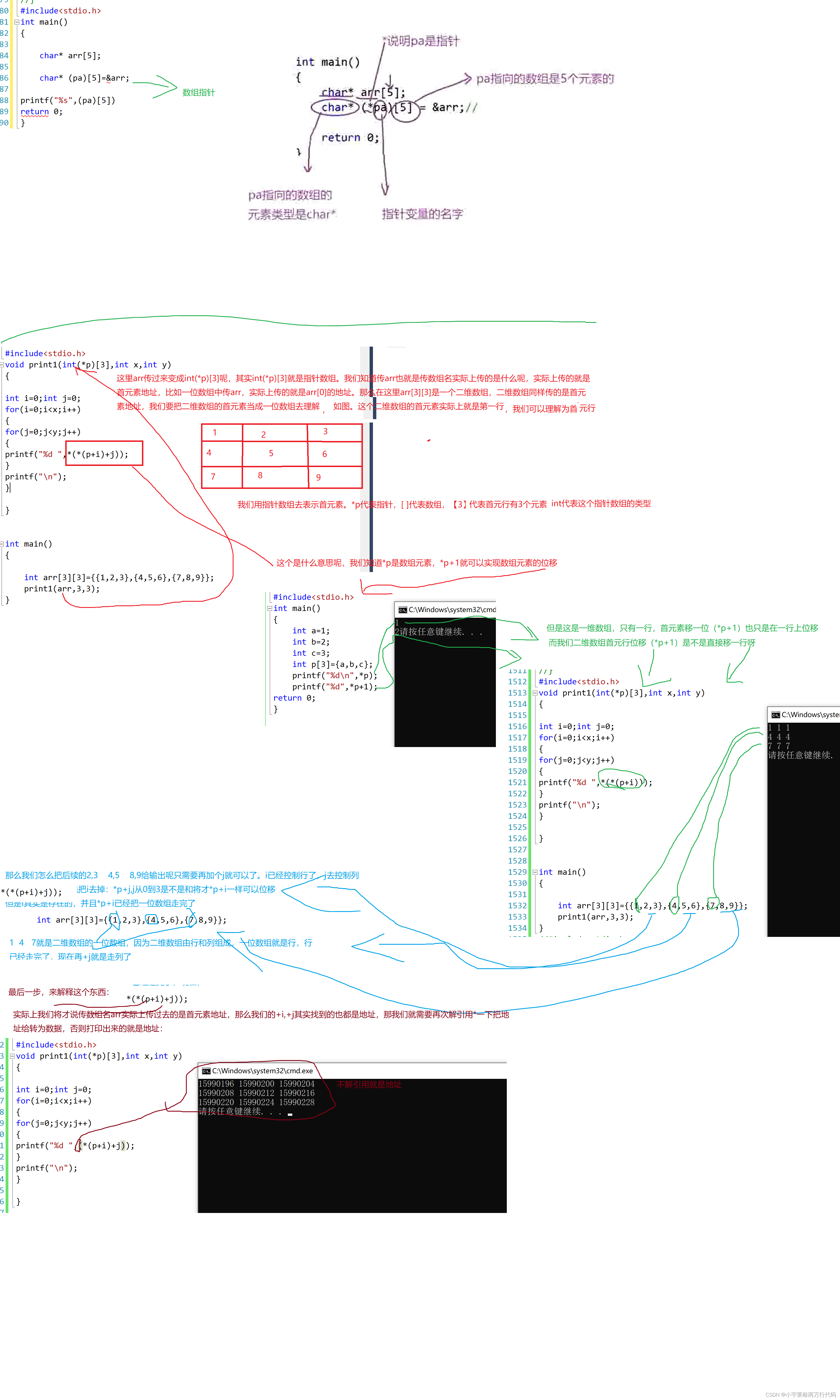
C语言 指针进阶笔记
p和*p: 如图,p是指针,指针存放着地址,打印出来应该是数组的值 *p是指针里里面的元素 #include<stdio.h> int main() {int a1;int b2;int c3;int p[3]{a,b,c};printf("%d",*p); return 0; } 那么现在的打印结果应该为数组的…...

数据库认证 | Oracle OCP好考吗
数据库对于很多技术人员来说都不陌生,但是你想深入了解的话,那么考个证书也许就是一个不错的选择。 如果能考个Oracle OCP认证的话,那也确实不错。那么Oracle OCP好考吗?下面我们就来了解一下吧。 01 Oracle OCP好考吗 OCP考试还…...

处理大数据的基础架构,OLTP和OLAP的区别,数据库与Hadoop、Spark、Hive和Flink大数据技术
处理大数据的基础架构,OLTP和OLAP的区别,数据库与Hadoop、Spark、Hive和Flink大数据技术 2022找工作是学历、能力和运气的超强结合体,遇到寒冬,大厂不招人,可能很多算法学生都得去找开发,测开 测开的话&am…...
解决计算机msvcp120.dll文件丢失的5种方法,亲测有效
在计算机使用过程中,我们经常会遇到一些错误提示,其中之一就是“msvcp120.dll丢失”。这个错误提示可能会给我们带来很大的困扰,影响我们的正常使用。本文将详细介绍msvcp120.dll丢失的原因、解决方法以及预防措施,帮助大家更好地…...

Python selenium交互
视频版教程:一天掌握python爬虫【基础篇】 涵盖 requests、beautifulsoup、selenium selenium可以模拟用户点击事件,以及控制浏览器前进,后退等操作。 下面是一个模拟百度搜索,点击下一页,控制浏览器后退,…...

基本微信小程序的体检预约小程序
项目介绍 我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,体检预约系统小程序被用户普遍使用,为方便用户…...

FHE 的高精度算术:BGV-big、BFV-big
参考文献: [NL11] Naehrig M, Lauter K, Vaikuntanathan V. Can homomorphic encryption be practical?[C]//Proceedings of the 3rd ACM workshop on Cloud computing security workshop. 2011: 113-124.[GC15] Geihs M, Cabarcas D. Efficient integer encoding…...
基于SpringBoot的在线笔记系统
技术介绍 🔥采用技术:SpringSpringMVCMyBatisJSPMaven 🔥开发语言:Java 🔥JDK版本:JDK1.8 🔥服务器:tomcat 🔥数据库:mysql 🔥数据库开发工具&…...
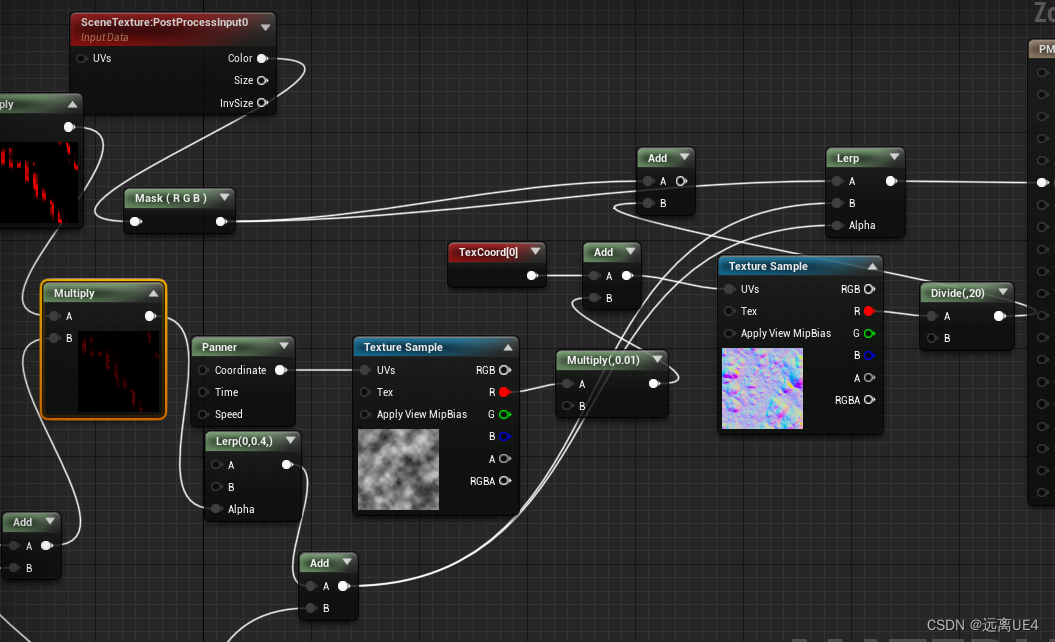
UE4 使用材质后期 制作玻璃有雨效果
效果展示,其实这是一个动画效果 以上为所有逻辑 拿到TexCoord给到Panner,Time和Speed都是通过下面计算而来,后面讲,再拿到时间和速度值过后,加上扰动值,最后取G值,因为雨事从上而下的动…...
:笔记检验概述)
笔记检验(一):笔记检验概述
文章目录 一、 笔迹的概念及成分(一) 笔迹的概念(二) 笔迹的成分 二、 笔迹检验的概念、任务及作用(一) 笔迹检验的概念(二) 笔迹检验的任务(三) 笔记检验的作…...

NOIP2023模拟6联测27 C. 点餐
NOIP2023模拟6联测27 C. 点餐 题目大意 有 n n n 种菜品,每样菜品有 a i , b i a_i , b_i ai,bi 假设有某位顾客点了 k k k 样菜品,那么价格为 ∑ i 1 k a p i max i 1 k b p i \sum_{i 1}^k a_{p_i}\max_{i 1}^kb_{p_i} ∑i1kapi…...

简单聊聊远程协同运维定义以及优势-行云管家
很多新人小伙伴对于远程协同运维不是很了解,今天我们就来简单聊聊远程协同运维定义以及优势。 远程协同运维定义 远程协同运维其实非常容易理解,主要是指计算机系统技术服务工程相关的人员通过局域网或者是其他网络对于它来进行连接,共同远…...

Ortec974A EPICS IOC程序
Ortec974A设备介绍,请见Ortec -- 974A 四通道100-MHz计时器/计数器_ortec974a_EPICS Technical的博客-CSDN博客 1) 创建一个用户存放这个IOC程序结构的目录: rootorangepi4-lts:/usr/local/EPICS/program# mkdir ortec974A rootorangepi4-l…...

JS-文件下载,实现在ios也是下载 而不是预览,
需求 通过A链接的方式,把从后台获取到的文件下载到本地,实现在移动端,PC端都能下载 问题 通过ajax请求后端生成的文件流之后,创建BLOB文件进行下载,在PC端和移动安卓端都可以实现下载到本地和对应的手机,而在IOS端的…...

Leetcode.275 H 指数 II
题目链接 Leetcode.275 H 指数 II mid 题目描述 给你一个整数数组 c i t a t i o n s citations citations ,其中 c i t a t i o n s [ i ] citations[i] citations[i] 表示研究者的第 i i i 篇论文被引用的次数, c i t a t i o n s citations citat…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...
