学习笔记|配对样本均数T检验|SPSS常用的快捷键|规范表达|《小白爱上SPSS》课程:SPSS第六讲 | 配对样本均数T检验
目录
- 学习目的
- 软件版本
- 原始文档
- 配对样本均数T检验
- 一、实战案例
- 二、案例解析
- 三、统计策略
- 四、SPSS操作
- 1、正态性检验
- 2、配对样本T检验
- 五、结果解读
- 六、规范报告
- 1、规范表格
- 2、规范文字
- 划重点
- Tips:SPSS常用的快捷键
学习目的
SPSS第六讲 | 配对样本均数T检验
软件版本
IBM SPSS Statistics 26。
原始文档
《小白爱上SPSS》课程
#统计原理
配对样本均数T检验
配对样本均数T检验,指的是使受试对象在某一或者某些状况、特征因素上相同或者基本相同的试验设计。
上一讲的两独立样本T检验的两组数据是独立的,无关联的。而配对样本T检验中,两组样本数据是匹配的,存有关联的。
配对样本T检验常常用于实验性研究设计中,主要有三种方案。
两种同质受试对象分别接受两种不同的处理(异体配对)
同一受试对象接受两组不同的处理(自身平行配对)
同一对象处理前后的结果进行比较(自身前后配对)
一、实战案例
小白想研究长时间持续运动对血尿酸浓度(mg%)的影响,让10名大侠在自行车功力计上持续运动上两个小时(负荷为100W/min),问长时间持续运动对大侠的血尿酸浓度有无影响?
读取数据:
GET FILE='E:\*************\小白爱上SPSS\小白数据\第六讲 配对样本t 检验.sav'.

二、案例解析
看到两组数据,小白比较迷惑:到底是采用两独立样本T检验还是配对样本T检验?答案很简单,关键看两样本是独立还是关联。两独立样本均数T检验主要是两组【独立】样本比较,比如男生和女生的身高比较。而配对样本均数T检验的两组样本是有关联的。比如本案例是同一样本进行前后比较,个体的运动前和运动后的血尿酸浓度存有关联,属于自身前后配对。因此,初步判断,可采用配对样本均数的T检验。
三、统计策略
统计分析策略口诀“目的引导设计,变量确定方法”。
针对上述案例,扪心六问。
Q1:本案例研究目的是什么?
A:比较差异。比较运动干预前后两组的总体均数是否存有差异
Q2:比较的组数是多少呢?
A:两组数据,且这两组数据前后匹配
Q3:本案例属于什么研究设计?
A:实验性研究
Q4:有几个变量?
A:两个变量。其中,测试次序是分组变量,血尿酸浓度是结局变量
Q5:变量类型是什么?
A:一个分组(分类)变量,分成前测和后测两组;另一个连续型变量,血尿酸浓度
Q6:连续型变量服从正态分布么?
A:需要对前后测量的差值进行检验,而不是两组的正态性检验。若服从,采用配对样本T检验;若不服从正态,采用配对秩和检验。
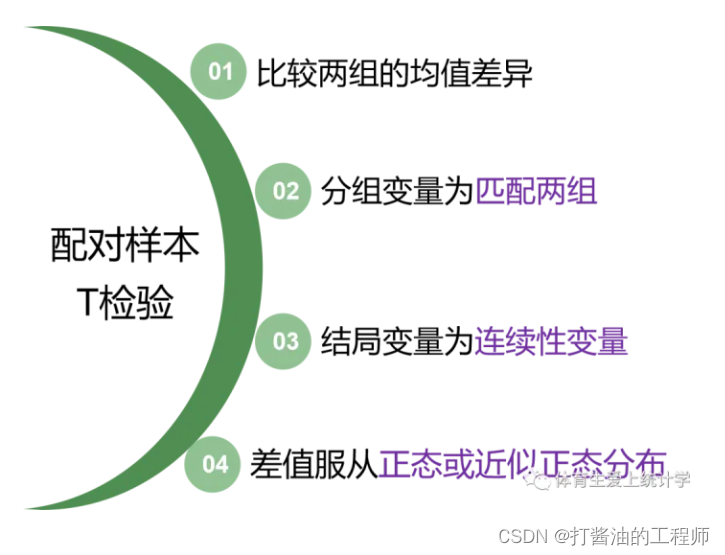
概括而言,如果数据满足以下条件,则采用配对样本T检验。
四、SPSS操作
1、正态性检验
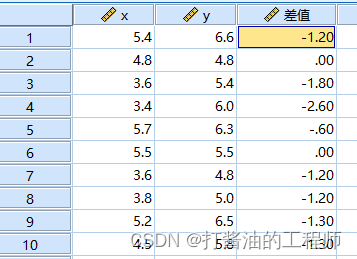
配对样本T检验的主要检验两组差值数据是否服从正态分布,为此,首先要计算运动干预前减去干预后的血尿酸的差值。
Step1:计算差值。
打开SPSS后,依次点击“转换”—“计算变量”,弹出对话框后,在目标变量中输入【差值】,在数据表达方式中,输入(x-y)【运动前-运动后】,注意:“运动前”和”运动后”可从类型和标签中放入。

点击确定后,在SPSS界面中就增加【差值】这一变量。
命令行:
COMPUTE 差值=x-y. /*计算差值(转换-计算变量)*/
EXECUTE /*执行*/.
Step2:对差值进行正态性检验
正态性检验的SPSS操作步骤请点击《第三讲 | 正态分布怎么检验?看这篇文章就够了》,这里只呈现检验结果。
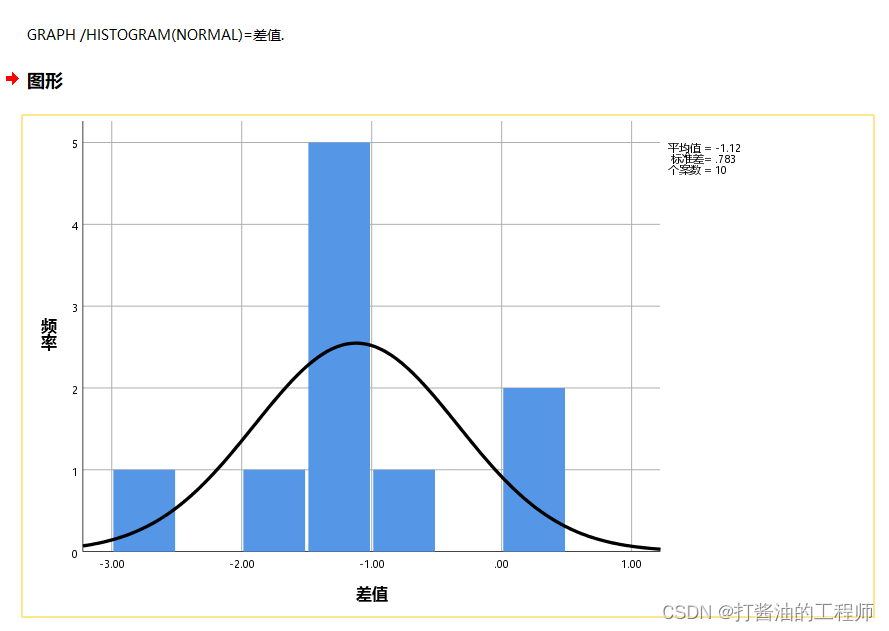
直方图绘制:
GRAPH /HISTOGRAM(NORMAL)=差值.
正态性检验:
EXAMINE VARIABLES=差值/PLOT BOXPLOT NPPLOT /*若无此行,则不输出正态性检验表*//COMPARE GROUPS /STATISTICS DESCRIPTIVES /CINTERVAL 95 /MISSING LISTWISE /NOTOTAL.

本案例样本量≤50时,以夏皮洛-威尔克(S-W)检验为准,p=0.314>0.05,无统计学意义(接受原假设:数据按正态分布)。同时结合直方图,可认为差值数据服从正态性分布。
2、配对样本T检验
原始假设:两组数据无相关性。
Step1:打开SPSS,依次点击:分析→比较平均值→成对样本T检验
Step2:会出现配对数据框Variable1与Variable2,把【运动前】和【运动后】分别放进对应位置
Step3: 点击确定,就可呈现统计结果。
命令行:
T-TEST PAIRS=x WITH y (PAIRED) /CRITERIA=CI(.9500) /MISSING=ANALYSIS.
五、结果解读
配对t检验结果有3张表。
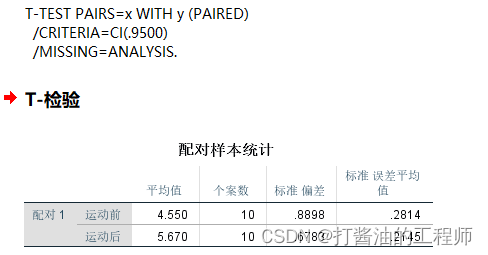
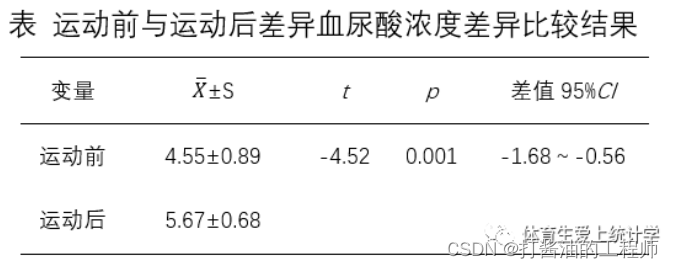
第1表:配对样本统计,运动前血尿酸浓度为4.55±0.89(mg%),运动后的浓度为5.67±0.68(mg%)。

第2表为两组数据相关性的统计学检验。本表不重要,它描述了配对数据的相关性程度和p值,本例相关性系数为0.529(该值范围从0-1,越大相关性越强,0.529属于具有一定的相关性,对原始假设存疑),P=0.116,表明它们相关系数没有达到显著性水平,其原因可能是样本量太少。事实上,受样本数量限制,在这里的P值没啥价值,关注相关系数即可。
第3表为配对t检验的结果,配对差值中的标准误差平均值为(.2814+.2415)/2=0.2476,(95%CI: -1.68,-0.56);检验统计量t=-4.524,p=0.001<0.05。配对差值与0值相比,差异具有统计学意义(不接受原始假设:两组数据无相关性)。
六、规范报告
规范报告有多种方式,本公众号只提供一种方式供参考。
1、规范表格
2、规范文字
由于数据服从正态分布,故采用配对样本均数的T检验。结果显示,长时间持续运动能显著提升血尿酸浓度t=-4.52,p=0.001,95%CI为(-1.68~-0.56)
小白将运动干预结果向主任报告,主任看后说:“看样子,给大侠们进行一次性运动干预还是有效果的,咱们就这么干,逐步扩大范围,让更多的组别参与干预”
小白心里嘀咕着 “更多组别,这怎么分析呀?”
主任看了小白一眼,“怎么啦,有难度吗?”
小白又一次挺直腰板说“没问题,不就是两两比较吗?”
主任向他诡异一笑,说“小白,你还是好好学习下一讲:单因素方差分析”
划重点
1、配对样本t检验来比较两个匹配样本的总体均数是否存有差异,一般用于实验性研究。
2、配对设计实验方案包括:异体配对、自身前后匹配、自身平行匹配。
3、配对样本t检验统计策略:分组变量为匹配两组、结局变量满足连续性、两组差值满足正态或近似正态分布。
Tips:SPSS常用的快捷键
引自:新手如何使用SPSS。
1.新建语法文件:Ctrl + N
2.打开数据文件:Ctrl + O
3.保存数据文件:Ctrl + S
4.关闭当前数据文件:Ctrl + F4
5.撤销上一步操作:Ctrl + Z
6.复制选中的内容:Ctrl + C
7.剪切选中的内容:Ctrl + X
8.粘贴内容:Ctrl + V
9.选择所有内容:Ctrl + A
10.运行选定项:Ctrl+R
11.关闭当前语法文件:Ctrl + F4
12.打开“数据编辑器”:Ctrl +1
13.打开“变量视图”:Ctrl +2
14.打开“输出视图”:Ctrl +3
15.打开“语法视图”:Ctrl +4
相关文章:

学习笔记|配对样本均数T检验|SPSS常用的快捷键|规范表达|《小白爱上SPSS》课程:SPSS第六讲 | 配对样本均数T检验
目录 学习目的软件版本原始文档配对样本均数T检验一、实战案例二、案例解析三、统计策略四、SPSS操作1、正态性检验2、配对样本T检验 五、结果解读六、规范报告1、规范表格2、规范文字 划重点Tips:SPSS常用的快捷键 学习目的 SPSS第六讲 | 配对样本均数T检验 软件版本 IBM S…...

python内置模块smtplib、email 发送电子邮件
一、简介 smtplib 是 Python 的标准库之一,用于发送电子邮件。它提供了一个简单的接口来连接到 SMTP(Simple Mail Transfer Protocol)服务器,并通过该服务器发送电子邮件。 email 是 Python 的标准库之一,用于处理电子…...

Qt使用QWebEngineView一些记录
1.关闭软件警告: Release of profile requested but WebEnginePage still not deleted. Expect troubles! 原因,系统退出关闭view,没有释放page。 解决办法:手动释放page 顺便把view也释放了。 Widget::~Widget() {updateIni…...

【2023.10.30练习】C语言-判断等式成立
计算机能力挑战初赛2020.20题 题目描述: 输入正整数A、B、C(0<A,B,C<10000),若用、-、*、/、%之一组成等式(即ABC,是上述运算符之一,),则输出“YES”,否则输出“NO”; 输入: 第一行输入…...
Wpf 使用 Prism 实战开发Day03
一.实现左侧菜单绑定 效果图: 1.首先需要在项目中创建 mvvm 的架构模式 创建 Models ,放置实体类。 实体类需要继承自Prism 框架的 BindableBase,目的是让实体类支持数据的动态变更! 例如: 系统导航菜单实体类 / <summary>/// 系统导航菜单实体类…...

JavaEE-cookie和session
本部分内容包括 cookie基本概念,sendcookies和getcookies代码; session基本概念,session实现登陆界面; 上述过程中涉及的代码如下: 1 import javax.servlet.ServletException; import javax.servlet.annotation.WebSe…...

Java设计模式之命令模式
目录 定义 结构 案例 优点 缺点 使用场景 JDK源码解析 Thread中start与run方法的区别 定义 将一个请求封装为一个对象,使发出请求的责任和执行请求的责任分割开。这样两者之间通过命令对象进行沟通,这样方便将命令对象进行存储、传递、调用、增…...

记录一段帮朋友写的代码,使用牛顿-拉夫逊方法解方程
要求 已知公式: t G A B F r B r 2 2 F A 2 B G A F ln ( r − A ) C o n s t t\frac{GAB}{F}r\frac{Br^2}{2F}\frac{A^2BGA}{F}\ln (r-A)Const tFGABr2FBr2FA2BGAln(r−A)Const 其中 t 的值为0-1000,每间隔25取一次值A2.12941E-10B0.…...

滑动窗口限流算法实现一
固定算法 原理:固定算法是将时间线分隔成固定大小的时间窗口,每个窗口都会有个计数器,用来记录窗口时间范围内的请求总数,如果窗口的请求总数达到最大限定值,会认定流量超限。比如将窗口大小设为1分钟,每分…...

简单明了!网关Gateway路由配置filters实现路径重写及对应正则表达式的解析
问题背景: 前端需要发送一个这样的请求,但出现404 首先解析请求的变化: http://www.51xuecheng.cn/api/checkcode/pic 1.请求先打在nginx,www.51xuecheng.cn/api/checkcode/pic部分匹配到了之后会转发给网关进行处理变成localho…...

EMQX内置Web管理控制台-Dashboard
一、Dashboard概述 EMQX Dashboard官网文档:https://docs.emqx.com/zh/enterprise/v5.1/dashboard/introduction.html 1、简介 EMQX 为用户提供了一个功能强大的内置管理控制台,即 EMQX Dashboard。通过这个控制台的 Web 界面,用户可以轻松监…...
计算机网络重点概念整理-第四章 网络层【期末复习|考研复习】
计算机网络复习系列文章传送门: 第一章 计算机网络概述 第二章 物理层 第三章 数据链路层 第四章 网络层 第五章 传输层 第六章 应用层 第七章 网络安全 计算机网络整理-简称&缩写 文章目录 前言四、网络层4.1 网络层功能4.1.1 电路交换、报文交换与分组交换4.1…...

数组转树形数据
const nodes [{ id: 3, name: 节点C, pid: 1 },{ id: 6, name: 节点F, pid: 3 },{ id: 0, name: root, pid: null },{ id: 1, name: 节点A, pid: 0 },{ id: 8, name: 节点H, pid: 4 },{ id: 4, name: 节点D, pid: 1 },{ id: 2, name: 节点B, pid: 0 },{ id: 5, name: 节点E, p…...

react动态插入样式
在开发组件过程中,偶尔需要动态的插入css,比如在在iframe中渲染组件后,iframe中是没有样式的,所以需要手动插入样式。 插入样式 通常是在useLayoutEffect中动态创建style标签 useLayoutEffect(() > {if (!ref.current) {cons…...
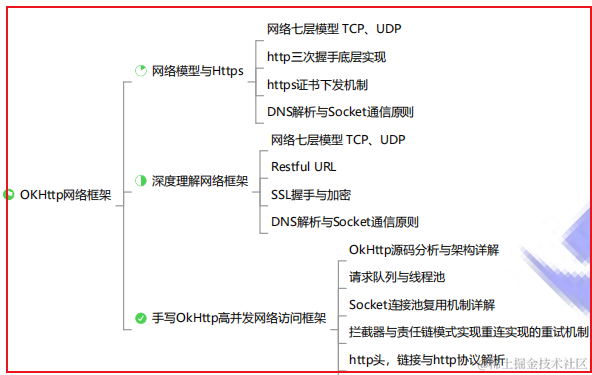
OkHttp网络框架深入理解-SSL握手与加密
OkHttp简介 由Square公司贡献的一个处理网络请求的开源项目,是目前Android使用最广泛的网络框架。从Android4.4开始HttpURLConnection的底层实现采用的是OkHttp。 特点: 支持HTTP/2并允许对同一主机的所有请求共享一个套接字通过连接池,减少了请求延迟…...
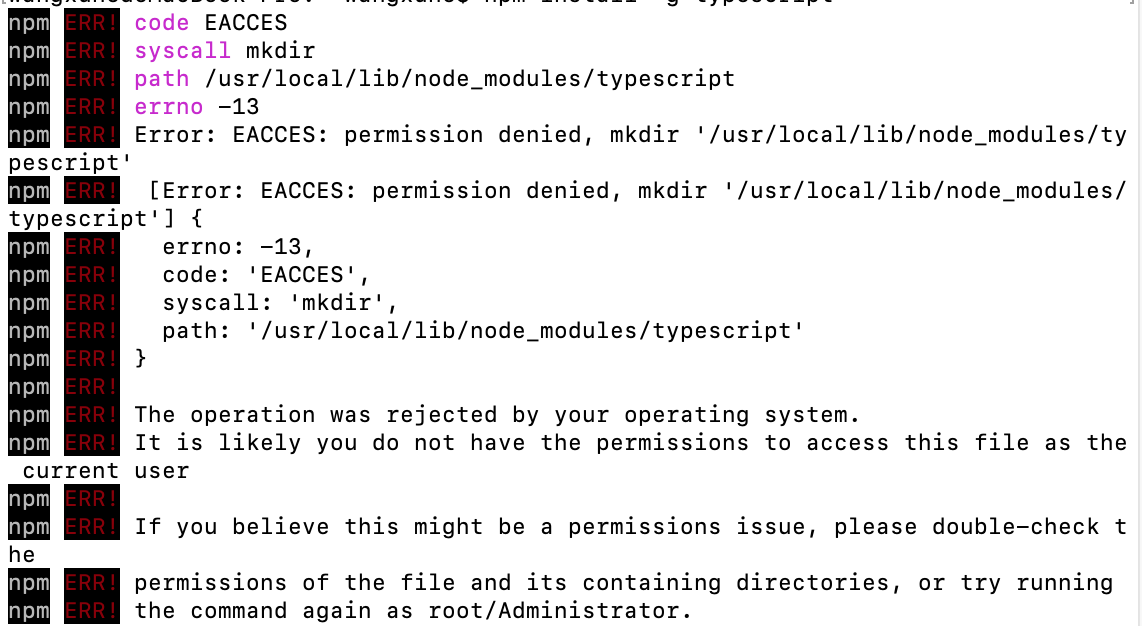
Mac 安装使用NPM及常用命令
环境: Mac 工具: NPM 可通过官网查询一些模块相关 NPM Doc 通过官网文档了解更多的关于NPM的使用 安装 NPM是Node.js的包管理工具,可用于解决 Node.js在代码部署上的问题。 新版本的Node.js已经集成了NPM, 因此可通过下载 Nod…...

利用 JSqlParser 防止 SQL 注入
高手文章《jsqlparser:实现基于SQL语法分析的SQL注入攻击检查》介绍了利用 JSqlParser 防止 SQL 注入,写得很好,只不过有两个问题,代码比较复杂,我于是作了简化,只有两个类;其次检测比较严格,连…...

10.27~10.29数电第三次实验分析与问题
实验要求 分析 寄存器 D触发器有两个输出口,一个输入口,一个时钟信号,一个复位信号 同步异步就是说复位信号在不在always里 给它加一个load就成了一位寄存器, 寄存器堆 8个8位的寄存器堆,每个寄存器都有两读一写…...
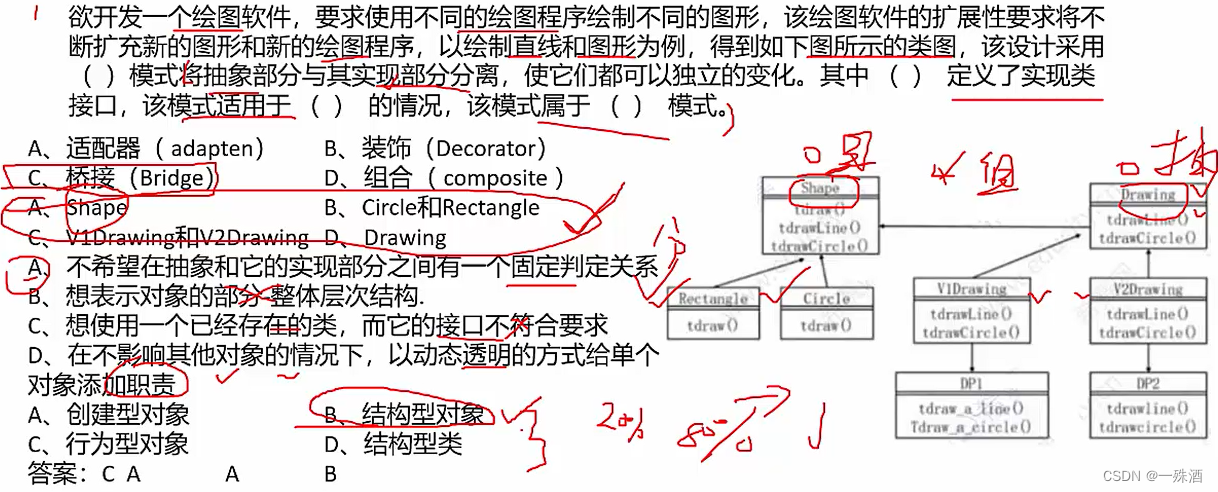
【软考】14.3 设计模式
《设计模式》 有下划线:类模式 / 对象模式无下划线:对象模式 创建型 设计模式 创建对象 构建器(Builder):类和构造分离抽象工厂(Abstract Factory):抽象接口工厂(Factor…...

Mac docker+vscode
mac 使用docker vs code 通过vscode 可以使用docker容器的环境。 可以在容器安装gdb, 直接调试代码。 创建容易时候可以指定目录和容易目录可以共享文件。...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...
