识别flink的反压源头
背景
flink中最常见的问题就是反压,这种情况下我们要正确的识别导致反压的真正的源头,本文就简单看下如何正确识别反压的源头
反压的源头
首先我们必须意识到现实中轻微的反压是没有必要去优化的,因为这种情况下是由于偶尔的流量峰值,TaskManager的GC,定时任务,或者网络波动正好触发引起的,我们要优化的是那种出现持续的反压的情况
其次反压是通过JobManager通过对TaskManager进行定时采样判断TaskManager的cpu状态来确定的,如下:
JobManager对多个采样周期的数据进行平均后得到如下参数:
idleTimeMsPerSecond 每秒空闲时间
busyTimeMsPerSecond 每秒繁忙时间
backPressuredTimeMsPerSecond 每秒反压时间
这里需要注意,既然是多个周期内的平均,需要意识到我们有可能处于这种情况,比如上一个采样cpu处于反压状态,下一个采样处于空闲状态,这种情况其实也值得注意
然后反压的定义如下:
OK: 0% <= back pressured <= 10%
LOW: 10% < back pressured <= 50%
HIGH: 50% < back pressured <= 100%
重新回到正题,比如如下的图:

我们看到Source算子和Flat map算子都处于严重的反压状态,那么导致反压的算子是哪一个呢?是Source算子和Flat Map算子本身吗?答案肯定不是,上游的算子反压都是由于下游算子的消费速度跟不上造成的,所以我们需要查看反压算子的下游算子,下游算子中cpu使用100%的那个下游算子几乎就是导致反压的真正源头,比如这里的keyed aggregate→map算子,cpu使用达到了100%,这才是我们需要优化的算子
PS: flink UI中展示的每个算子的cpu空闲/忙碌/反压值是算子所有算子任务中的最大子任务的cpu空闲/最大子任务的cpu忙碌/最大子任务的cpu反压的值
相关文章:

识别flink的反压源头
背景 flink中最常见的问题就是反压,这种情况下我们要正确的识别导致反压的真正的源头,本文就简单看下如何正确识别反压的源头 反压的源头 首先我们必须意识到现实中轻微的反压是没有必要去优化的,因为这种情况下是由于偶尔的流量峰值,Task…...

Spring是如何解决bean循环依赖的问题的
在Spring框架中,循环依赖是指两个或多个Bean之间相互依赖,形成了一个闭环的依赖关系。当存在循环依赖时,Bean的创建过程会陷入死循环,导致应用程序无法启动或出现异常。 说到循环依赖,首先我先说说bean的三级缓存 在S…...
[移动通讯]【Carrier Aggregation-9】【 Radio Resource Control (RRC) Aspects】
前言: CA 分析辅助工具: UE Capabilities 目录: 总体流程 Radio Resource Control (RRC) Aspects SCell addition and removal Handover 一 总体流程 1.1 CA 总体流程 1.2 CA 和 NSA 区别 NSA 我理解也是一种特殊的CA 方案&…...

故障预测与健康管理(PHM)的由来以及当前面临的挑战
故障预测与健康管理(PHM)作为一项关键技术,旨在帮助企业在事故发生之前较长时间内实现故障预测与健康管理,达到“治未病”的效果。PHM的发展源于对设备可靠性和安全性的追求,以及对预测性维护的需求。然而,…...

【ChatGPT瀑布到水母】AI 在驱动软件研发的革新与实践
这里写目录标题 前言内容简介作者简介专家推荐读者对象目录直播预告 前言 计算机技术的发展和互联网的普及,使信息处理和传输变得更加高效,极大地改变了金融、商业、教育、娱乐等领域的运作方式。数据分析、人工智能和云计算等新兴技术,也在不…...

【Django】项目模型
Django的基本命令 django-admin 命令含义startproject启动Django项目startapp启动Django应用check检查项目完整性runserver本地运行项目shell进入Django项目的Python Shell环境test 进行Django用例测试makemigrations创建模型变更的迁移文件migrate执行makemigrations…...
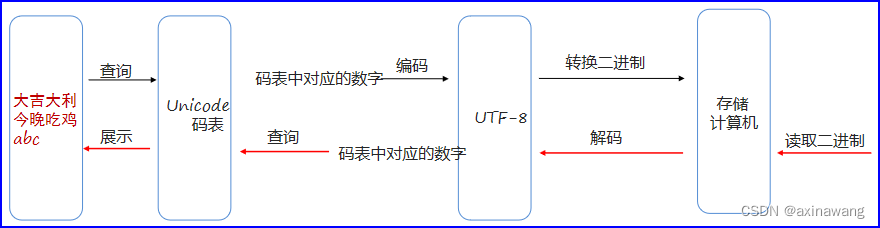
字符集详解
常见字符集介绍 字符集基础知识: 计算机底层不可以直接存储字符的。 计算机中底层只能存储二进制(0、1) 。 二进制是可以转换成十进制的。 结论:计算机底层可以表示成十进制编号。计算机可以给人类字符进行编号存储,这套编号规则就是字符…...

Vert.x学习笔记-什么是Vert.x
Vert.x介绍 用官网的一句话来总结:Vert.x是用于在JVM上构建响应式应用程序的工具包,项目初期的目标是成为“JVM版的Node.js”,但是后续的发展逐渐偏离了初期的目标,变成了一个给JVM提供量身定制的异步编程基础框架的工具包。 Ver…...

AcWing 第127场周赛 构造矩阵
构造题目,考虑去除掉最后一行最后一列先进行考虑,假设除了最后一行和最后一列都已经排好了(你可以随便排),那么分析知最后一个数字由限制以外其他都已经确定了,无解的情况是k为-1 并且n,m的奇偶…...
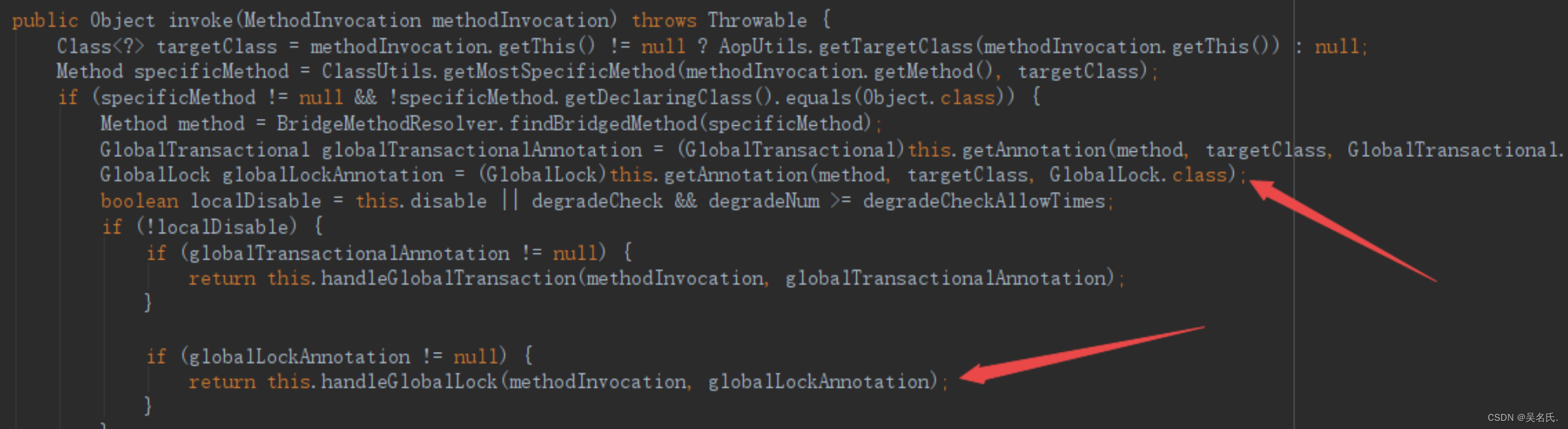
Seata入门系列【15】@GlobalLock注解使用场景及源码分析
1 前言 在Seata 中提供了一个全局锁注解GlobalLock,字面意思是全局锁,搜索相关文档,发现资料很少,所以分析下它的应用场景和基本原理,首先看下源码中对该注解的说明: // 声明事务仅在单个本地RM中执行 //…...
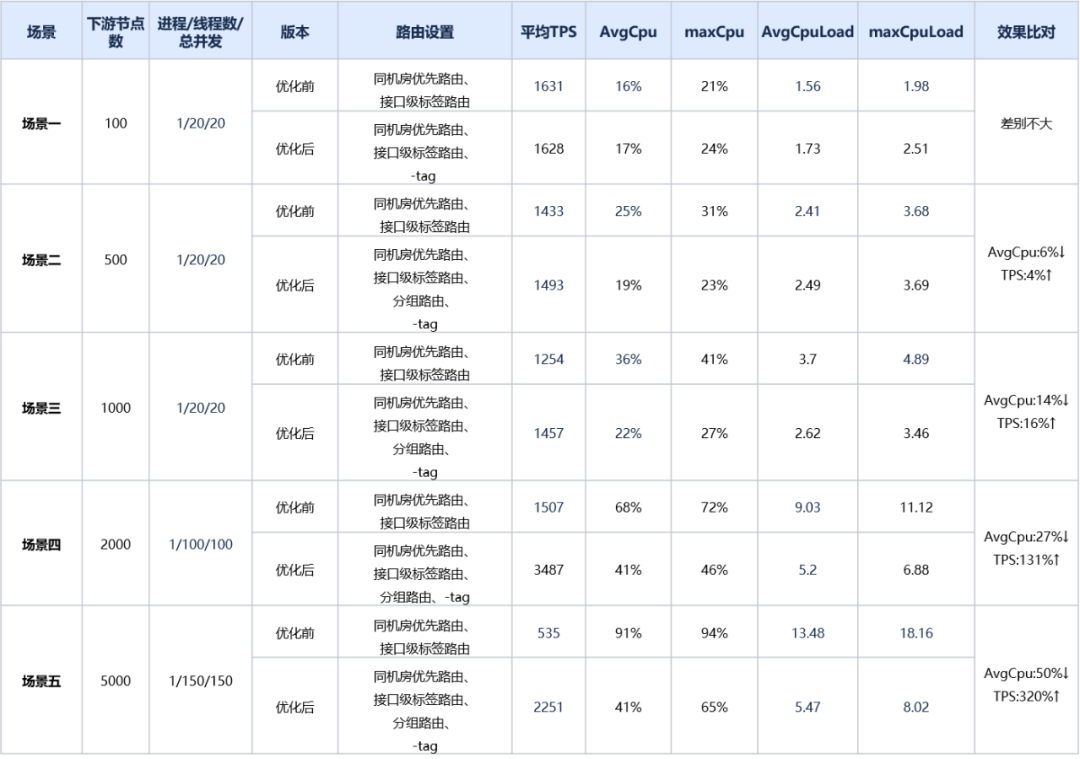
Dubbo 路由及负载均衡性能优化
作者:vivo 互联网中间件团队- Wang Xiaochuang 本文主要介绍在vivo内部针对Dubbo路由模块及负载均衡的一些优化手段,主要是异步化缓存,可减少在RPC调用过程中路由及负载均衡的CPU消耗,极大提升调用效率。 一、概要 vivo内部Java…...

Python数据可视化入门指南
Matplotlib和Plotly是两个在Python中广泛使用的数据可视化库,它们具有丰富的API和功能,用于创建各种类型的图表和图形。在本篇博客中,我们将介绍它们的主要特点和基本用法。 Matplotlib 主要特点: 高度自定义: Matp…...
我的ChatGPT的几个使用场景
示例一,工作辅助、写函数代码: 这里展示了一个完整的代码,修正,然后最终输出的过程。GPT具备足够丰富的相关的小型代码生成能力,语法能力也足够好。这类应用场景,在我的GPT使用中,能占到65%以上…...
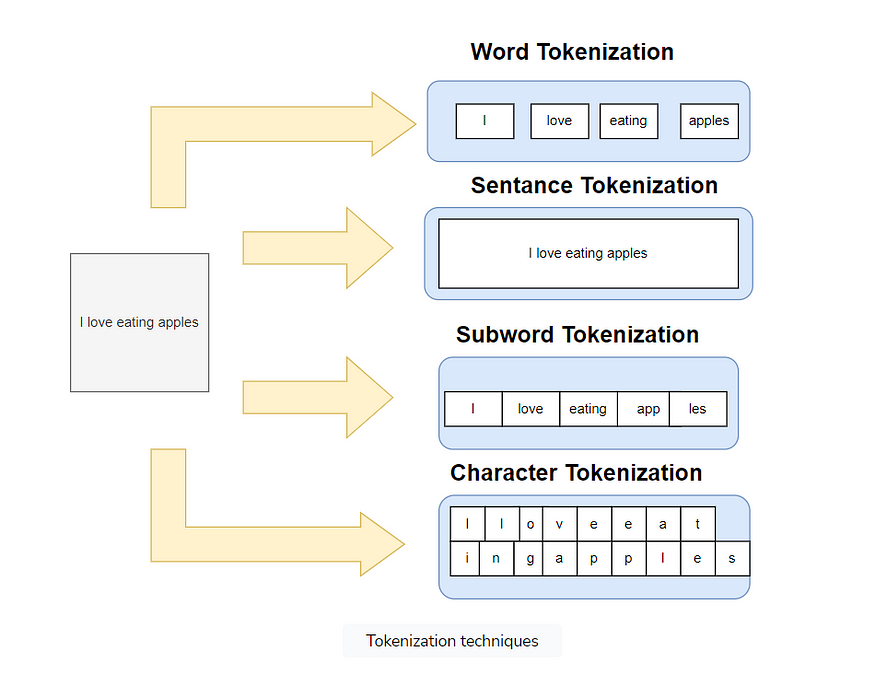
3 — NLP 中的标记化:分解文本数据的艺术
一、说明 这是一个系列文章的第三篇文章, 文章前半部分分别是: 1 — NLP 的文本预处理技术2 — NLP中的词干提取和词形还原:文本预处理技术 在本文中,我们将介绍标记化主题。在开始之前,我建议您阅读我之前介绍…...

C++-类与对象(上)
一、 auto关键字 1.自动识别数据类型 2.auto的初始化 3.auto简化for循环 nullptr的使用 二、类与对象 1.c中类的定义 2.c语言与c的比较 3.类的访问限定符以及封装 3.1访问限定符 3.2封装 3.3类的作用域 3.4类的声明与定义分离 🗡CSDN主页:d1ff1cult.&…...

多进程间通信学习之无名管道
无名管道:首先它是内核空间的实现机制;然后只能用于亲缘进程间通信;它在内核所占的大小是64KB;它采用半双工的通信方式;请勿使用lseek函数;读写特点:若读端存在写管道,那么有多少数据…...

flink常用的几种调优手段的优缺点
背景: 不管是基于减少反压还是基于减少端到端的延迟的目的,我们有时候都需要对flink进行调优,本文就整理下几种常见的调优手段以及他们的优缺点 flink调优手段 1.使用事件时间EventTime模式时,可以设置水位线发送的时间间隔,比…...

如何选择安全又可靠的文件数据同步软件?
数据实时同步价值体现在它能够确保数据在多个设备或系统之间实时更新和保持一致。这种技术可以应用于许多领域,如电子商务、社交媒体、金融服务等。在这些领域中,数据实时同步可以带来很多好处,如提高工作效率、减少数据不一致、提高用户体验…...

使用反射调用类的私有内部类的私有方法
文章目录 使用反射调用类的私有方法类实现方法实现代码 使用反射调用类的私有内部类的私有方法类实现方法实现代码 在进行单元测试时,我们往往需要直接访问某个类的内部类或者某个类的私有方法,此时正常的调用就无能为力了,因此我们可以使用反…...

记一次 AWD 比赛中曲折的 Linux 提权
前提背景: 今天一场 AWD 比赛中,遇到一个场景:PHP网站存在SQL注入和文件上传漏洞, MYSQL当前用户为ROOT,文件上传蚁剑连接SHELL是权限很低的用户。我需要想办法进行提权,才能读取到 /root 目录下的 flag。 一、sqlmap …...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...
