Leetcode 542. 01 矩阵
542. 01 矩阵-中等
问题描述
给定一个由 0 和 1 组成的矩阵 mat ,请输出一个大小相同的矩阵,其中每一个格子是 mat 中对应位置元素到最近的 0 的距离。
两个相邻元素间的距离为 1 。
示例 1:
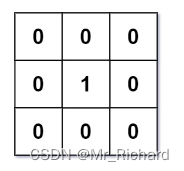
输入:mat = [[0,0,0],[0,1,0],[0,0,0]]
输出:[[0,0,0],[0,1,0],[0,0,0]]
示例 2:
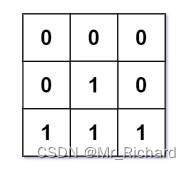
输入:mat = [[0,0,0],[0,1,0],[1,1,1]]
输出:[[0,0,0],[0,1,0],[1,2,1]]
提示:
m == mat.lengthn == mat[i].length1 <= m, n <= 1041 <= m * n <= 104mat[i][j] is either 0 or 1.mat中至少有一个0
解题思路与代码实现一
采用BFS搜索解题:
- 创建标记数组visited用于标记已访问过的元素,初始化均为Integer.MAX_VALUE(不小于可能的最大步长m+n-1),因为在BFS的过程中,先被访问的元素的步长一定小于等于后被访问的元素;创建队列queue用于实现BFS,初始化均为false;
- 扫描mat数组,需要把所有
mat[i][j]为0的元素加入队列并标记为已访问; - 接着扫描队列,当队列不为空时,队头元素出队,依次访问其上下左右的周围点,如果未发生数组越界且该周围点没被访问过,则将其入队并标记为已访问(true),同时更新周围点的步长 = 出队元素的步长 +1;
public int[][] updateMatrix2(int[][] mat) {// m、n分别表示矩阵的行数和列数int m = mat.length, n = mat[0].length;// 依次表示 上、左、下、右周围四个点的偏移量int[][] dirs = {{-1, 0}, {0, -1}, {1, 0}, {0, 1}};// BFS用的队列Queue<int[]> queue = new LinkedList<>();// 标记数组boolean[][] visited = new boolean[m][n];for (int i = 0; i < m; i++) {// 标记数组初始化全为false,mat[i][j]为0的元素会被标记为trueArrays.fill(visited[i], false);for (int j = 0; j < n; j++) {if (mat[i][j] == 0) {// mat[j][j]为0的元素标记为true并优先入队visited[i][j] = true;queue.offer(new int[]{i, j});} else {mat[i][j] = Integer.MAX_VALUE;}}}while (!queue.isEmpty()) {// 从队列中取出访问过的一个元素作为当前点,访问其周围点int[] current = queue.poll();int currentX = current[0];int currentY = current[1];for (int[] dir : dirs) {// 依次表示 上、左、下、右周围四个点的x、y坐标int x = currentX + dir[0];int y = currentY + dir[1];// 如果坐标未越界,且该周围点mat[x][y]未被访问过(由BFS概念可知,先被访问的的mat[i][j]一定不会超过后访问的)// 也可以不使用标记数组,替换为判断 不越界 且 当前点的距离小于周围点(mat[currentX][currentY] < mat[x][y]),但效率却更低些if (x >= 0 && x < m && y >= 0 && y < n && !visited[x][y]) {// 标记访问过,并入队visited[x][y] = true;queue.offer(new int[]{x, y});// 更新值mat[x][y] = mat[currentX][currentY] + 1;}}}return mat;
}
解题思路与代码实现二
采用动态规划:
先找最优子结构,很明显,一个点的最短距离应该是它周围上下左右四个点(如果存在的话)的最短距离+1,即:

dp[i][j]表示(i,j)到0的最短距离,但由于0所在位置不固定,所以先将dp数组初始化:mat[i][j]为0,则dp[i][j]取0,否则dp[i][j]取20000(最长距离:m+n-1=19999<20000)。然后为分两轮进行比较:
- 第一轮从左到右从上到下扫描mat数组,
dp[i][j]取mat[i-1][j]+1、mat[i][j-1]+1和dp[i][j]的最小值,需要注意下标越界; - 第二轮从右到左从下到上扫描mat数组,
dp[i][j]取mat[i][j+1]+1、mat[i+1][j]+1和dp[i][j]的最小值,需要注意下标越界;
两轮扫描结束后,dp[i][j]表示(i,j)到0的最短距离,即为所求
public int[][] updateMatrix(int[][] mat) {// m、n分别表示矩阵的行数和列数int m = mat.length, n = mat[0].length;// dp数组int[][] dp = new int[m][n];// dp数组初始化for (int i = 0; i < m; i++) {for (int j = 0; j < n; j++) {// 19999为1 <= m, n <= 104条件下,可能出现的最大长度 m + n -1dp[i][j] = mat[i][j] == 0 ? 0 : 20000;}}// 先更新左边和上边的最小值for (int i = 0; i < m; i++) {for (int j = 0; j < n; j++) {// 判断上边是否越界if (i - 1 >= 0) {dp[i][j] = Math.min(dp[i - 1][j] + 1, dp[i][j]);}// 判断左边是否越界if (j - 1 >= 0) {dp[i][j] = Math.min(dp[i][j - 1] + 1, dp[i][j]);}}}// 再更新右边和下边的最小值for (int i = m - 1; i >= 0; i--) {for (int j = n - 1; j >= 0; j--) {if (i + 1 < m) {dp[i][j] = Math.min(dp[i + 1][j] + 1, dp[i][j]);}if (j + 1 < n) {dp[i][j] = Math.min(dp[i][j + 1] + 1, dp[i][j]);}}}return dp;}
参考链接:
【LeetCode】 542. 01 矩阵 动态规划 dp
LeetCode] 542. 01 Matrix 零一矩阵
相关文章:

Leetcode 542. 01 矩阵
542. 01 矩阵-中等 问题描述 给定一个由 0 和 1 组成的矩阵 mat ,请输出一个大小相同的矩阵,其中每一个格子是 mat 中对应位置元素到最近的 0 的距离。 两个相邻元素间的距离为 1 。 示例 1: 输入:mat [[0,0,0],[0,1,0],[0…...
分享一下微信小程序抽奖链接怎么做
标题:微信小程序抽奖链接制作全攻略,轻松玩转营销抽奖活动 一、引言 在当今的数字化时代,抽奖活动已经成为一种高效的市场营销策略,而微信小程序作为一个功能强大的移动端平台,为企业和个人提供了制作抽奖链接的便捷…...
MathType2024破解版激活序列号
MathType序列号是一款针对该软件而制作的激活工具,大家都知道这款软件在官方是需要花钱购买的,不然得话就只能试用。有很多功能都无法正常使用!而本序列号却可以完美的解决这一难题,因为它可以破解并激活“MathType”,…...

简述对 Spring MVC 的理解
SpringMVC 是一种基于 Java 语言开发,实现了 Web MVC 设计模式,请求驱动类型的轻量级 Web 框架。 Spring MVC组件 MVC 架构模式的思想,通过把 Model,View,Controller 分离,将 Web 层进行职责解耦࿰…...
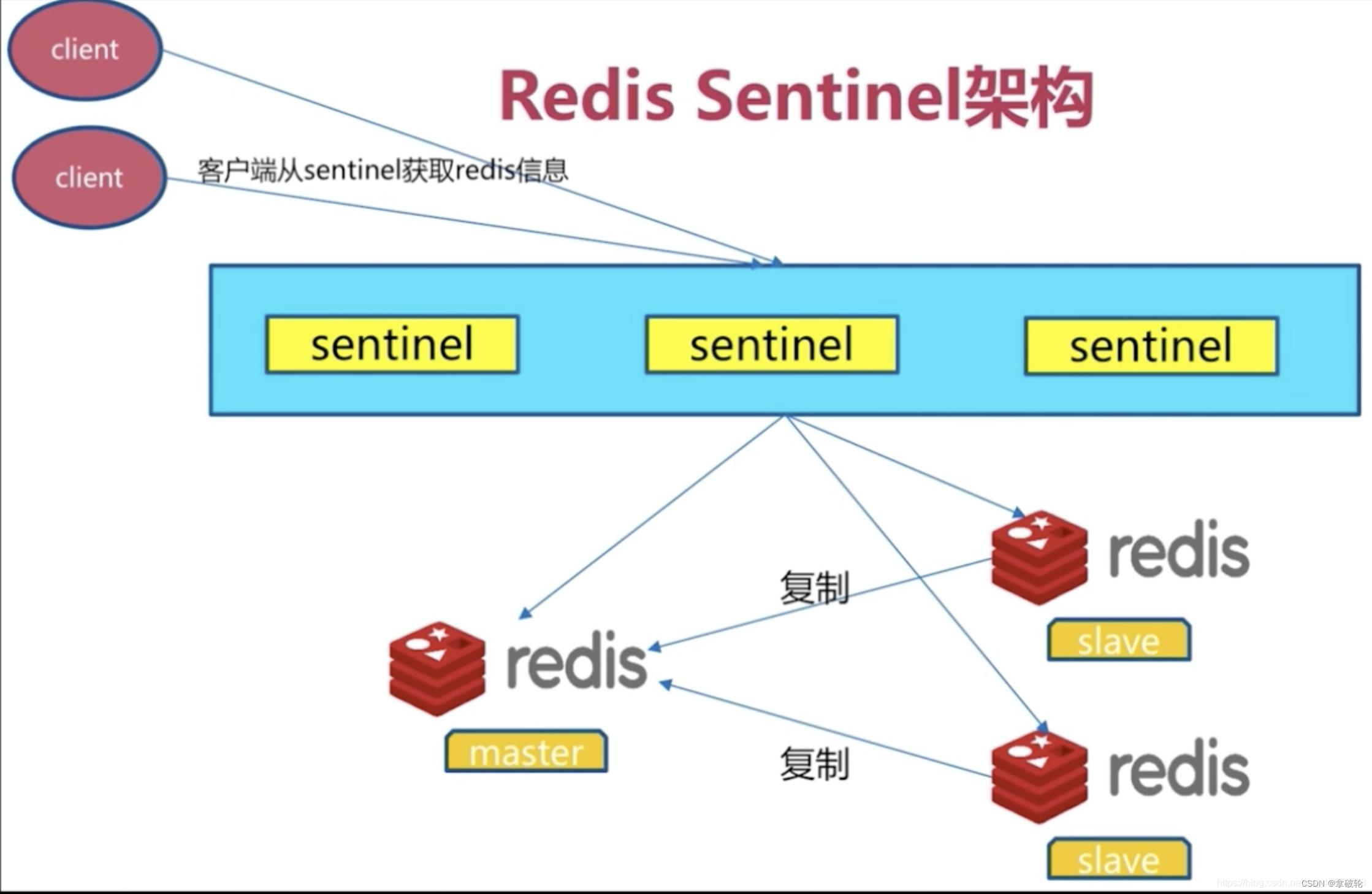
Redis——哨兵模式与Zookeeper选举的异同点
摘要 当我们使用主从复制出现的问题:手动故障转移:写能力和存储能力受限:主从复制 -master 宕机故障处理。 主从切换技术的方法是:当主服务器宕机后,需要手动把一台从服务器切换为主服务器,这就需要人工干…...

基于 Center 的 3D 目标检测和跟踪
论文地址:https://arxiv.org/abs/2006.11275 论文代码:https://github.com/tianweiy/CenterPoint 3D 目标通常表示为点云中的 3D Boxes。 CenterPoint 在第一阶段,使用关键点检测器检测对象的中心,然后回归到其他属性࿰…...
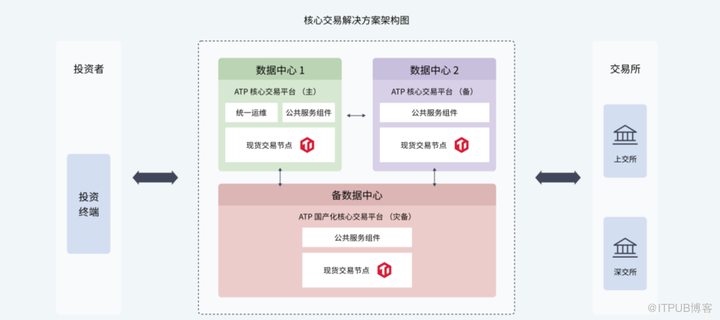
华锐技术何志东:证券核心交易系统分布式改造将迎来规模化落地阶段
近年来,数字化转型成为证券业发展的下一战略高地,根据 2021 年证券业协会专项调查结果显示,71% 的券商将数字化转型列为公司战略任务。 在落地数字化转型战略过程中,证券业核心交易系统面临着不少挑战。构建新一代分布式核心交易…...

数据结构 -- ArrayList与LinkedList的区别
一、二者的相同点 1,它们都是继承自List接口。 二、二者的区别 1,数据结构:ArrayList是(Array动态数组)的数据结构;而LinkedList是(Link双向链表)的数据结构。ArrayList 自由性较…...

豪车托运为什么选小板
小板运输是一种适用于豪车客户的高效运输方式。它提供了快速、安全、便捷的服务,并且相对经济实惠。以下是关于小板运输的时效和价格的介绍: 时效:小板运输通常能够在短时间内完成车辆的运输。具体时效取决于起点和目的地之间的距离ÿ…...

【base64加密】js/ts的基础加密
base64的字符串简单加密,主用于网页缓存数据的加密。 适用于常规html、小游戏(egret、cocos、laya)等 原文参考:JS基于base64编码加密解密文本和图片(修订)_js base64加密-CSDN博客 测试:JS实…...
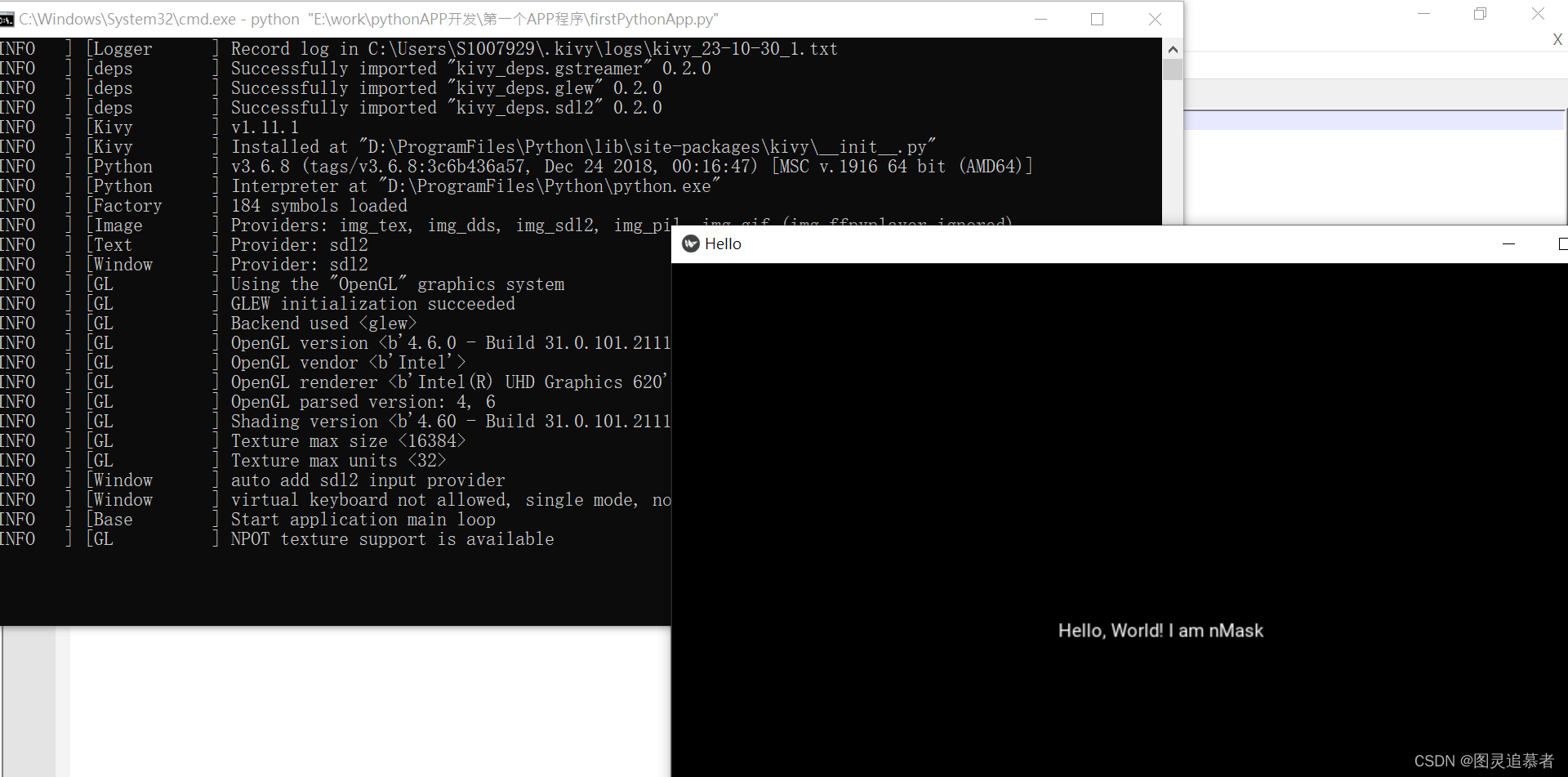
基于python的app程式开发
安装的库文件: 运行代码: # -*- coding:utf-8 -*- from kivy.app import App class HelloApp(App):pass if __name__ __main__:HelloApp().run() 结果画面:...

Spring Event学习
Spring Event学习 观察者模式是一种行为设计模式,它定义了对象之间的依赖关系,当一个对象的状态发生改变时,所有依赖于它的对象都会得到通知并被自动更新。在这个模式中,改变状态的对象被称为主题,依赖的对象被称为观…...

UE4 HLSL学习笔记
在Custom配置对应ush文件路径 在HLSL中写入对应代码 Custom里面增加两个Input,名字必须和ush文件内的未知变量名字一样 然后就对应输出对应效果的颜色 这就是简单的加法运算 减法同理: 乘法除法同理 HLSL取最小值 HLSL取最大值 绝对值: 取余…...
报文的路由过程
路由转发过程 记住路由转发过程结论:报文ip是不变,mac改变。 mac地址在同一个广播域传输过程中是不变的;在跨越广播域的时候会发生改变的;而IP地址在传输过程中是不会改变的(除NAT的时候)。 ip地址本质上是…...

【CPP】类和对象
1- Classes and Objects Structures A struct in C is a type consisting of a sequence of data membersSome functions/Statements are needed to operate the data members of an object of a struct type 不不小心操作错误,不小心越界 Classes You should b…...

【多线程面试题二十】、 如何实现互斥锁(mutex)?
文章底部有个人公众号:热爱技术的小郑。主要分享开发知识、学习资料、毕业设计指导等。有兴趣的可以关注一下。为何分享? 踩过的坑没必要让别人在再踩,自己复盘也能加深记忆。利己利人、所谓双赢。 面试官:如何实现互斥锁…...

hypercube背景设置为白色,绘制高光谱3D立方体
import scipy pip install wxpython PyOpenGL和Spectral需要本地安装 可参考链接https://blog.csdn.net/qq_43204333/article/details/119837870 参考:https://blog.csdn.net/Tiandailan/article/details/132719745?spm1001.2014.3001.5506Mouse Functions:left-cl…...
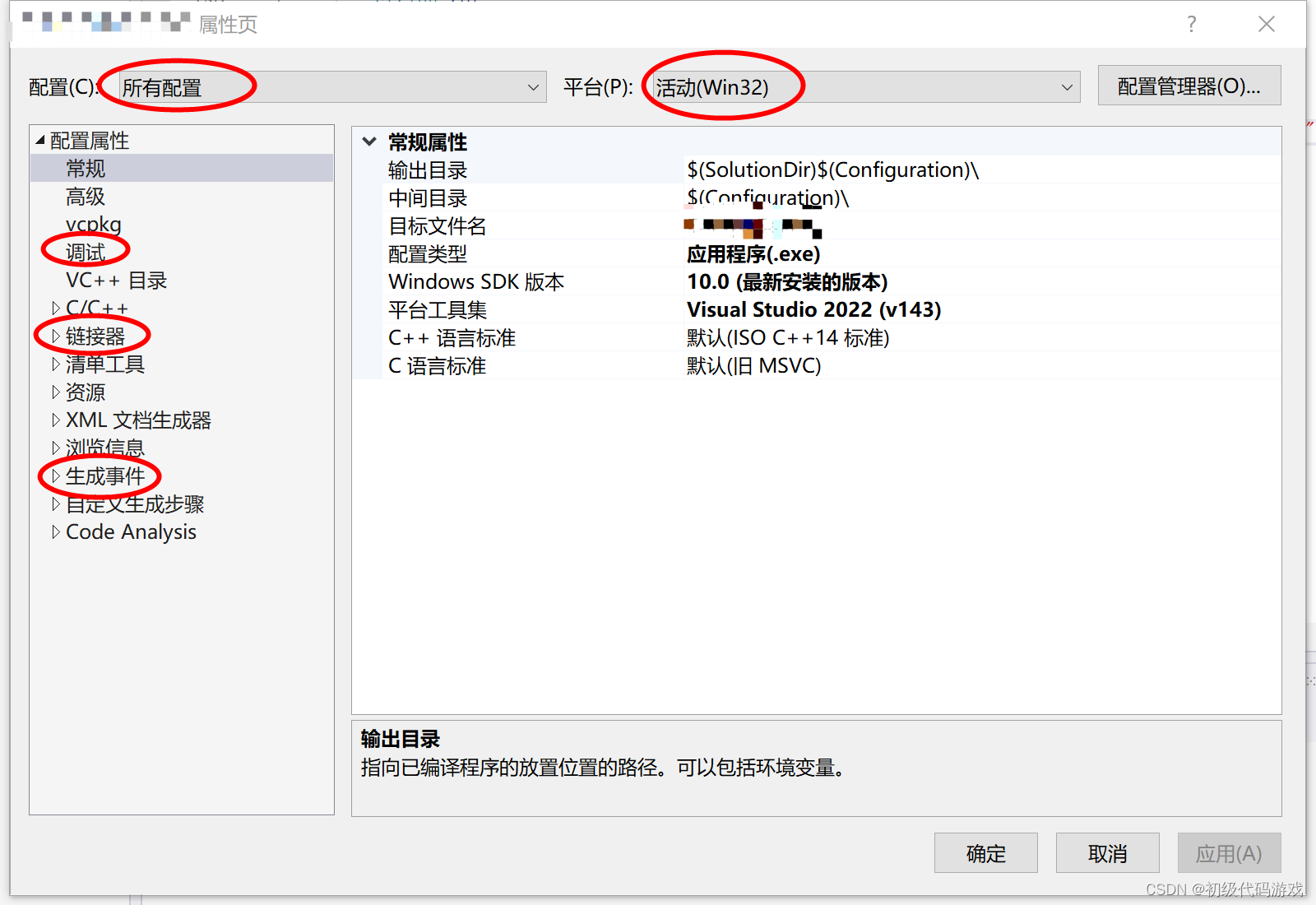
Visual Studio(VS)C++项目 管理第三方依赖库和目录设置
发现很多程序员存在这种做法:把项目依赖的第三方库的lib和dll放在项目目录下,或者复制到输出目录,因为每种配置都有不同的输出目录,所以要复制多份(至少包括Debug和Release两个输出目录),这些做…...

leetCode 2578. 最小和分割 + 排序 + 贪心 + 奇偶分组(构造最优解)
2578. 最小和分割 - 力扣(LeetCode) 给你一个正整数 num ,请你将它分割成两个非负整数 num1 和 num2 ,满足: num1 和 num2 直接连起来,得到 num 各数位的一个排列。 换句话说,num1 和 num2 中所…...

自定义实现图片裁剪
要实现这个功能,首先需要创建一个自定义的View,然后在该View中绘制背景框和裁剪后的图片。以下是一个简单的实现: 1. 创建一个名为CustomImageView的自定义View类,继承自View: import android.content.Context; impor…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

解析奥地利 XARION激光超声检测系统:无膜光学麦克风 + 无耦合剂的技术协同优势及多元应用
在工业制造领域,无损检测(NDT)的精度与效率直接影响产品质量与生产安全。奥地利 XARION开发的激光超声精密检测系统,以非接触式光学麦克风技术为核心,打破传统检测瓶颈,为半导体、航空航天、汽车制造等行业提供了高灵敏…...

从面试角度回答Android中ContentProvider启动原理
Android中ContentProvider原理的面试角度解析,分为已启动和未启动两种场景: 一、ContentProvider已启动的情况 1. 核心流程 触发条件:当其他组件(如Activity、Service)通过ContentR…...

aardio 自动识别验证码输入
技术尝试 上周在发学习日志时有网友提议“在网页上识别验证码”,于是尝试整合图像识别与网页自动化技术,完成了这套模拟登录流程。核心思路是:截图验证码→OCR识别→自动填充表单→提交并验证结果。 代码在这里 import soImage; import we…...
