leetCode 2578. 最小和分割 + 排序 + 贪心 + 奇偶分组(构造最优解)
2578. 最小和分割 - 力扣(LeetCode)
给你一个正整数 num ,请你将它分割成两个非负整数 num1 和 num2 ,满足:
num1和num2直接连起来,得到num各数位的一个排列。- 换句话说,
num1和num2中所有数字出现的次数之和等于num中所有数字出现的次数。
- 换句话说,
num1和num2可以包含前导 0 。
请你返回 num1 和 num2 可以得到的和的 最小 值。
注意:
num保证没有前导 0 。num1和num2中数位顺序可以与num中数位顺序不同。

思路分析总结来自:(https://leetcode.cn/problems/split-with-minimum-sum/)
- 1.满足nums1 和 nums2的位数小于<= bit_len(num) / 2 尽可能最短
- 2.依次给nums1 和 nums2 分配较小的数给高位
(1)用一个 nums数组 来存放num的各个位的数字,然后 sort排序,再根据思路分析将其转化为num1 和 num2
class Solution {
public:int splitNum(int num) {vector<int> nums;while(num){nums.push_back(num%10);num = num / 10;}sort(nums.begin(),nums.end());int num1=0,num2=0;for(int i=0;i<nums.size();i++) {if(i%2==0) num1 = num1 * 10 + nums[i];else num2 = num2 * 10 + nums[i];}return num1 + num2;}
};这段文字来自这篇博客:位运算&1,」」1,「「1
n&1 就是判断 n 是否为奇数.
- n 为奇数时,对应的二进制数最低位一定为1,n&1的结果就是1。
- n为偶数时,相应的最低位为0,n&1的结果就是0。
- n&1 ==1 或者写 n%2 == 1 或者写 n%2
可以将i%2 == 1 写成 i&1
class Solution {
public:int splitNum(int num) {vector<int> nums;while(num){nums.push_back(num%10);num = num / 10;}sort(nums.begin(),nums.end());int num1=0,num2=0;for(int i=0;i<nums.size();i++) {if(i&1) num2 = num2 * 10 + nums[i];else num1 = num1 * 10 + nums[i];}return num1 + num2;}
};(2) 将num先转成字符串,接着根据思路分析,拼接两个字符串s1和s2,最后转成int,相加后返回
class Solution {
public:int splitNum(int num) {string s = to_string(num);sort(s.begin(),s.end());string s1,s2;for(int i=0;i<s.size();i++) {// if(i&1) s2 += s[i];// else s1 += s[i];i&1?s2 += s[i] : s1 += s[i];}return stoi(s1) + stoi(s2);}
};(3)将num先转成字符串,接着根据思路分析,获得num1和num2,相加后返回
class Solution {
public:int splitNum(int num) {string s = to_string(num);sort(s.begin(),s.end());int num1=0,num2=0;for(int i=0;i<s.size();i++) {// if(i&1==1) num2 = num2 * 10 + s[i]-'0';// else num1 = num1 * 10 + s[i]-'0';i&1? num2 = num2 * 10 + s[i]-'0' : num1 = num1 * 10 + s[i]-'0';}return num1 + num2;}
};(4)将(3)进行进一步优化,省去三目运算
class Solution {
public:int splitNum(int num) {string s = to_string(num);sort(s.begin(),s.end());int a[2]{};for(int i=0;i<s.size();i++) {// a[i % 2] = a[i % 2] * 10 + s[i] - '0'; a[i&1] = a[i&1] * 10 + s[i]-'0';}return a[0] + a[1];}
};- 时间复杂度:O(mlogm),其中 m 为 num 转成字符串后的长度。
- 空间复杂度:O(m)
相关文章:

leetCode 2578. 最小和分割 + 排序 + 贪心 + 奇偶分组(构造最优解)
2578. 最小和分割 - 力扣(LeetCode) 给你一个正整数 num ,请你将它分割成两个非负整数 num1 和 num2 ,满足: num1 和 num2 直接连起来,得到 num 各数位的一个排列。 换句话说,num1 和 num2 中所…...

自定义实现图片裁剪
要实现这个功能,首先需要创建一个自定义的View,然后在该View中绘制背景框和裁剪后的图片。以下是一个简单的实现: 1. 创建一个名为CustomImageView的自定义View类,继承自View: import android.content.Context; impor…...

开发语言工具编程系统化教程入门和初级专辑课程上线
开发语言工具编程系统化教程入门和初级专辑课程上线 学习编程捷径:(不论是正在学习编程的大学生,还是IT人士或者是编程爱好者,在学习编程的过程中用正确的学习方法 可以达到事半功倍的效果。对于初学者,可以通过下面…...
【Truffle】二、自定义合约测试
一、准备测试 上期我们自己安装部署了truffle,并且体验了测试用例的整个测试流程,实际开发中,我们可以对自己的合约进行测试。 我们首先先明白自定义合约测试需要几个文件 合约文件:既然要测试合约,肯定要有合约的源码…...

场景交易额超40亿,海尔智家三翼鸟开始收获
文 | 螳螂观察 作者 | 余一 随着双十一的到来,国内的消费情绪再次被点燃。在这类大促之下,品牌们就像一个个天体,不断引动着市场潮汐,期待自己能触发更大的“海潮效应”。 所谓“海潮效应”是指,海水因天体的引力而…...

众和策略可靠吗?股票扛杆怎么玩?
可靠 股票扛杆是一种出资战略,经过假贷资金来增加出资金额,从而进步出资收益。这种战略在股票商场中被广泛运用,但一起也伴随着一定的危险。在本文中,咱们将从多个视点来剖析股票扛杆怎么玩。 首要,扛杆出资的原理是…...
: Lost connection to MySQL server at ‘waiting)
解决连接Mysql出现ERROR 2013 (HY000): Lost connection to MySQL server at ‘waiting
在上一篇中解决Mysql ER_ACCESS_DENIED_ERROR: Access denied for user ‘root‘‘localhost‘ (using password: YES)-CSDN博客 写了mysql的密码报错问题,在执行 mysql -u root -p 出现了这个错误, ERROR 2013 (HY000): Lost connection to MySQL se…...

Hadoop YARN功能介绍--资源管理、调度任务
Hadoop YRAN介绍 YARN是一个通用资源管理系统平台和调度平台,可为上层应用提供统一的资源管理和 调度。 他的引入为集群在利用率、资源统一管理和数据共享等方面带来了好处。 1.资源管理系统 集群的硬件资源,和程序运行无关,比如内存、cu…...

从AlexNet到chatGPT的演进过程
一、演进 AlexNet(2012): AlexNet是深度学习领域的重要突破,包括5个卷积层和3个全连接层。使用ReLU激活函数和Dropout正则化,获得了ImageNet图像分类比赛的胜利。引入了GPU加速训练,大幅提高了深度神经网络…...

Unity如何实现bHaptics TrackSuit震动衣的SDK接入
前言 TrackSuit是bHaptisc公司旗下的一款震动衣,包括X16,X40等不同型号,是一款尖端的无线高级触觉背心,采用人体工程学设计,具有40个精确的触觉反馈点。通过无缝的跨平台支持和无限制、无滞后的游戏体验,增强您的VR冒险体验。用于PC或者VR游戏中高度还原真实射击触感。官…...

识别flink的反压源头
背景 flink中最常见的问题就是反压,这种情况下我们要正确的识别导致反压的真正的源头,本文就简单看下如何正确识别反压的源头 反压的源头 首先我们必须意识到现实中轻微的反压是没有必要去优化的,因为这种情况下是由于偶尔的流量峰值,Task…...

Spring是如何解决bean循环依赖的问题的
在Spring框架中,循环依赖是指两个或多个Bean之间相互依赖,形成了一个闭环的依赖关系。当存在循环依赖时,Bean的创建过程会陷入死循环,导致应用程序无法启动或出现异常。 说到循环依赖,首先我先说说bean的三级缓存 在S…...
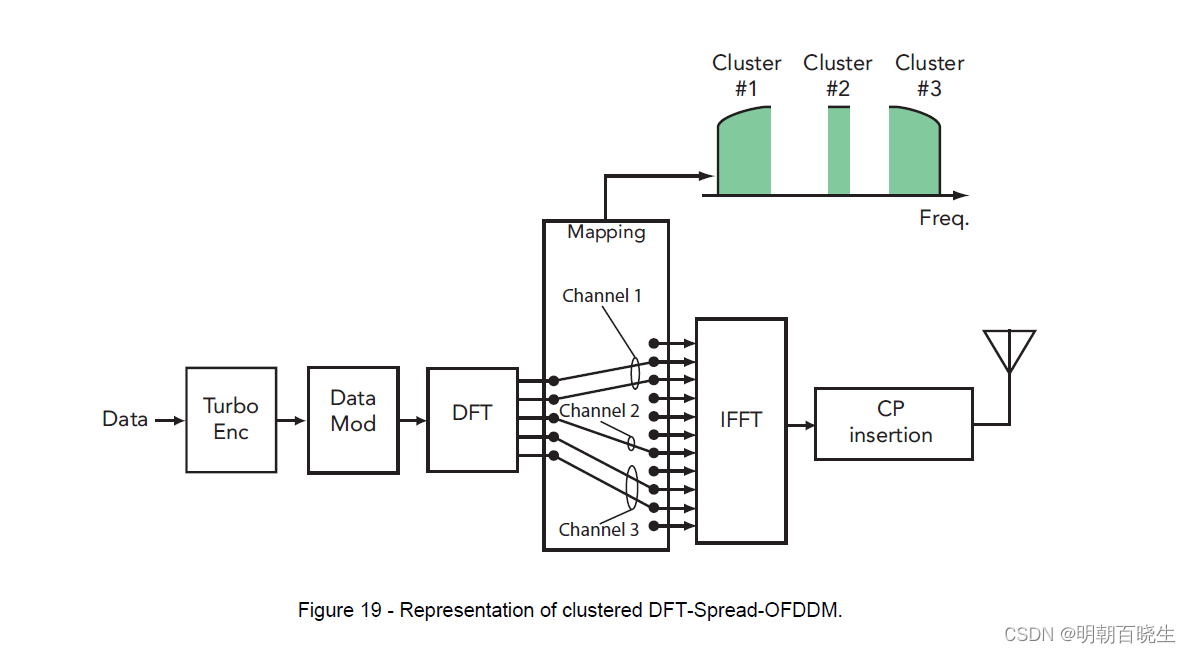
[移动通讯]【Carrier Aggregation-9】【 Radio Resource Control (RRC) Aspects】
前言: CA 分析辅助工具: UE Capabilities 目录: 总体流程 Radio Resource Control (RRC) Aspects SCell addition and removal Handover 一 总体流程 1.1 CA 总体流程 1.2 CA 和 NSA 区别 NSA 我理解也是一种特殊的CA 方案&…...

故障预测与健康管理(PHM)的由来以及当前面临的挑战
故障预测与健康管理(PHM)作为一项关键技术,旨在帮助企业在事故发生之前较长时间内实现故障预测与健康管理,达到“治未病”的效果。PHM的发展源于对设备可靠性和安全性的追求,以及对预测性维护的需求。然而,…...

【ChatGPT瀑布到水母】AI 在驱动软件研发的革新与实践
这里写目录标题 前言内容简介作者简介专家推荐读者对象目录直播预告 前言 计算机技术的发展和互联网的普及,使信息处理和传输变得更加高效,极大地改变了金融、商业、教育、娱乐等领域的运作方式。数据分析、人工智能和云计算等新兴技术,也在不…...

【Django】项目模型
Django的基本命令 django-admin 命令含义startproject启动Django项目startapp启动Django应用check检查项目完整性runserver本地运行项目shell进入Django项目的Python Shell环境test 进行Django用例测试makemigrations创建模型变更的迁移文件migrate执行makemigrations…...
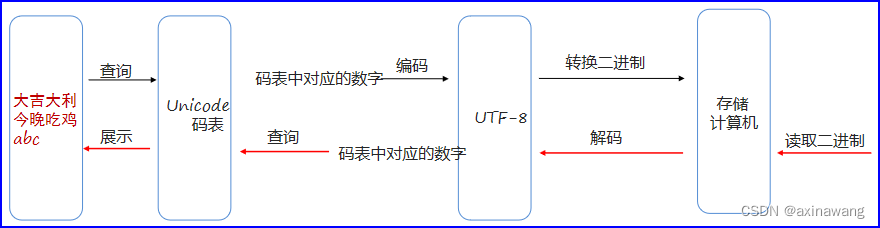
字符集详解
常见字符集介绍 字符集基础知识: 计算机底层不可以直接存储字符的。 计算机中底层只能存储二进制(0、1) 。 二进制是可以转换成十进制的。 结论:计算机底层可以表示成十进制编号。计算机可以给人类字符进行编号存储,这套编号规则就是字符…...

Vert.x学习笔记-什么是Vert.x
Vert.x介绍 用官网的一句话来总结:Vert.x是用于在JVM上构建响应式应用程序的工具包,项目初期的目标是成为“JVM版的Node.js”,但是后续的发展逐渐偏离了初期的目标,变成了一个给JVM提供量身定制的异步编程基础框架的工具包。 Ver…...

AcWing 第127场周赛 构造矩阵
构造题目,考虑去除掉最后一行最后一列先进行考虑,假设除了最后一行和最后一列都已经排好了(你可以随便排),那么分析知最后一个数字由限制以外其他都已经确定了,无解的情况是k为-1 并且n,m的奇偶…...
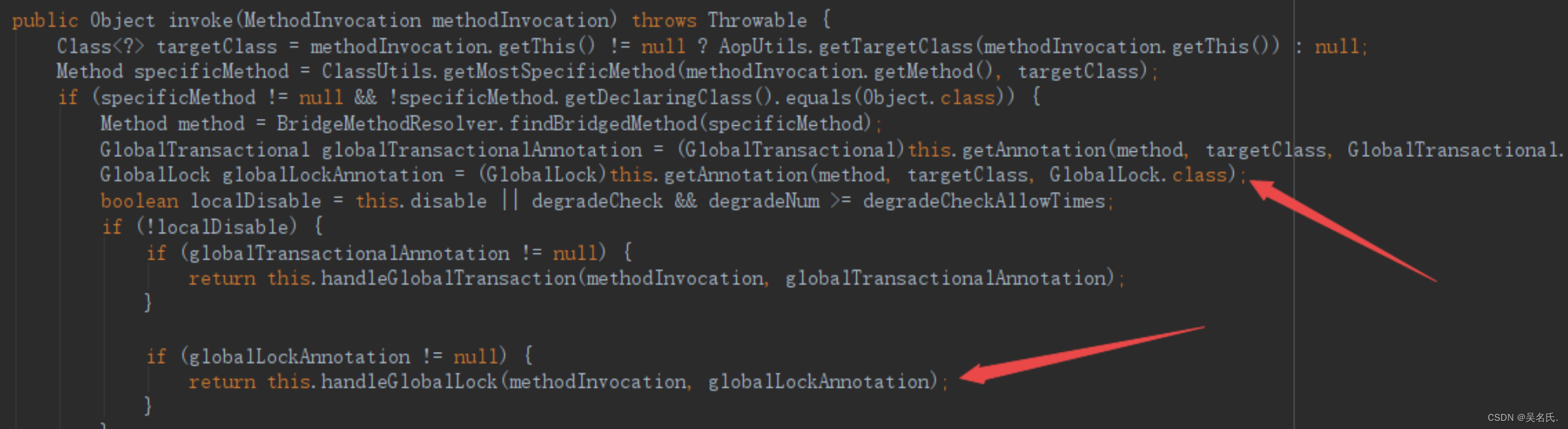
Seata入门系列【15】@GlobalLock注解使用场景及源码分析
1 前言 在Seata 中提供了一个全局锁注解GlobalLock,字面意思是全局锁,搜索相关文档,发现资料很少,所以分析下它的应用场景和基本原理,首先看下源码中对该注解的说明: // 声明事务仅在单个本地RM中执行 //…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...

Scrapy-Redis分布式爬虫架构的可扩展性与容错性增强:基于微服务与容器化的解决方案
在大数据时代,海量数据的采集与处理成为企业和研究机构获取信息的关键环节。Scrapy-Redis作为一种经典的分布式爬虫架构,在处理大规模数据抓取任务时展现出强大的能力。然而,随着业务规模的不断扩大和数据抓取需求的日益复杂,传统…...

华为OD机试-最短木板长度-二分法(A卷,100分)
此题是一个最大化最小值的典型例题, 因为搜索范围是有界的,上界最大木板长度补充的全部木料长度,下界最小木板长度; 即left0,right10^6; 我们可以设置一个候选值x(mid),将木板的长度全部都补充到x,如果成功…...

vue3 daterange正则踩坑
<el-form-item label"空置时间" prop"vacantTime"> <el-date-picker v-model"form.vacantTime" type"daterange" start-placeholder"开始日期" end-placeholder"结束日期" clearable :editable"fal…...

OCR MLLM Evaluation
为什么需要评测体系?——背景与矛盾 能干的事: 看清楚发票、身份证上的字(准确率>90%),速度飞快(眨眼间完成)。干不了的事: 碰到复杂表格(合并单元…...

用 Rust 重写 Linux 内核模块实战:迈向安全内核的新篇章
用 Rust 重写 Linux 内核模块实战:迈向安全内核的新篇章 摘要: 操作系统内核的安全性、稳定性至关重要。传统 Linux 内核模块开发长期依赖于 C 语言,受限于 C 语言本身的内存安全和并发安全问题,开发复杂模块极易引入难以…...

CMS内容管理系统的设计与实现:多站点模式的实现
在一套内容管理系统中,其实有很多站点,比如企业门户网站,产品手册,知识帮助手册等,因此会需要多个站点,甚至PC、mobile、ipad各有一个站点。 每个站点关联的有站点所在目录及所属的域名。 一、站点表设计…...
