【数据结构】排序算法总结
⭐ 作者:小胡_不糊涂
🌱 作者主页:小胡_不糊涂的个人主页
📀 收录专栏:浅谈数据结构
💖 持续更文,关注博主少走弯路,谢谢大家支持 💖
总结
- 1. 归并排序
- 2. 计数排序
- 3. 排序算法复杂度及稳定性分析

在总结之前我们先介绍一下归并排序和计数排序!
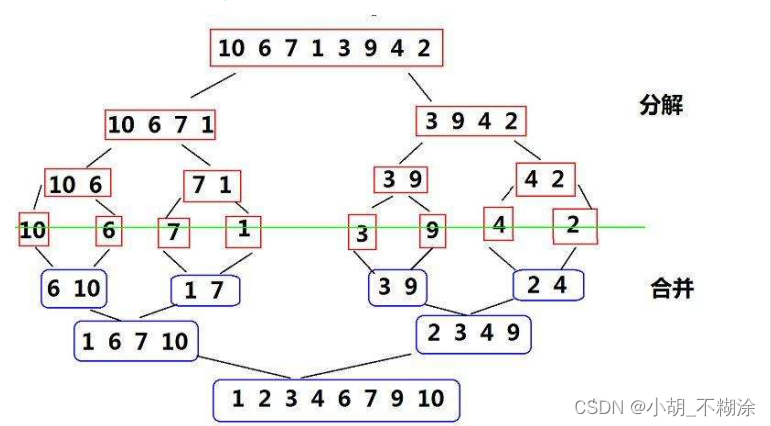
1. 归并排序
归并排序(MERGE-SORT) 是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide andConquer)的一个非常典型的应用。
将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。 归并排序核心步骤:
代码实现:
/*** 归并排序* 时间复杂度:O(N*logN)* 空间复杂度:O(logN)* 稳定性:稳定的排序* 目前为止3个稳定的排序:直接插入排序、冒泡排序、归并排序* @param array*/public static void mergeSort(int[] array){mergeSortFun(array,0,array.length-1);}private static void mergeSortFun(int[] array,int start,int end){if(start>=end){return;}//拆分int mid=(start+end)/2;mergeSortFun(array,start,mid);mergeSortFun(array,mid+1,end);merge(array,start,mid,end);//合并}private static void merge(int[] array,int left,int mid,int right){//定义拆分后的左边部分int s1=left;int e1=mid;//定义拆分后的右边部分int s2=mid+1;int e2=right;//定义一个新数组存放合并后的数据int[] tmp=new int[right-left+1];int i=0;//tmp的下标//同时满足-证明两个归并段都有数据while(s1<=e1&& s2<=e2){if(array[s1]<=array[s2]){tmp[i++]=array[s1++];}else{tmp[i++]=array[s2++];}}while(s1<=e1){tmp[i++]=array[s1++];}while (s2 <= e2) {tmp[i++]=array[s2++];}//把排好序的数据 拷贝回原来的数组array当中for(int j=0;j<tmp.length;j++){array[j+left]=tmp[j];}}
归并排序可以解决海量数据的排序问题:
外部排序:排序过程需要在磁盘等外部存储进行的排序
前提: 内存只有 1G,需要排序的数据有 100G
因为内存中因为无法把所有数据全部放下,所以需要外部排序,而归并排序是最常用的外部排序。
- 先把文件切分成 200 份,每个 512 M
- 分别对 512 M 排序,因为内存已经可以放的下,所以任意排序方式都可以
- 进行 2 路归并,同时对 200 份有序文件做归并过程,最终结果就有序了
2. 计数排序
基本思想: 计数排序又称为鸽巢原理,是对哈希直接定址法的变形应用。 操作步骤:
- 统计相同元素出现次数
- 根据统计的结果将序列回收到原来的序列中
代码实现:
/*** 计数排序的场景:* 指定范围内的数据* 时间复杂度: O(MAX(N,范围))* 空间复杂度:O(范围)* 稳定性:稳定的排序* @param array*/public static void countSort(int[] array) {//寻找最大值、最小值int maxvalue=array[0];int minvalue=array[0];for(int i=0;i<array.length;i++){if(array[i]>maxvalue){maxvalue=array[i];}if(array[i]<minvalue){minvalue=array[i];}}int[] countarr=new int[maxvalue-minvalue+1];//记录array中元素出现个数,初始值都为0for(int i=0;i<array.length;i++){countarr[array[i]-minvalue]++;}int index=0;//重新定义array下标for(int i=0;i<countarr.length;i++){while(countarr[i]>0){array[index]=i+minvalue;index++;countarr[i]--;}}}
3. 排序算法复杂度及稳定性分析
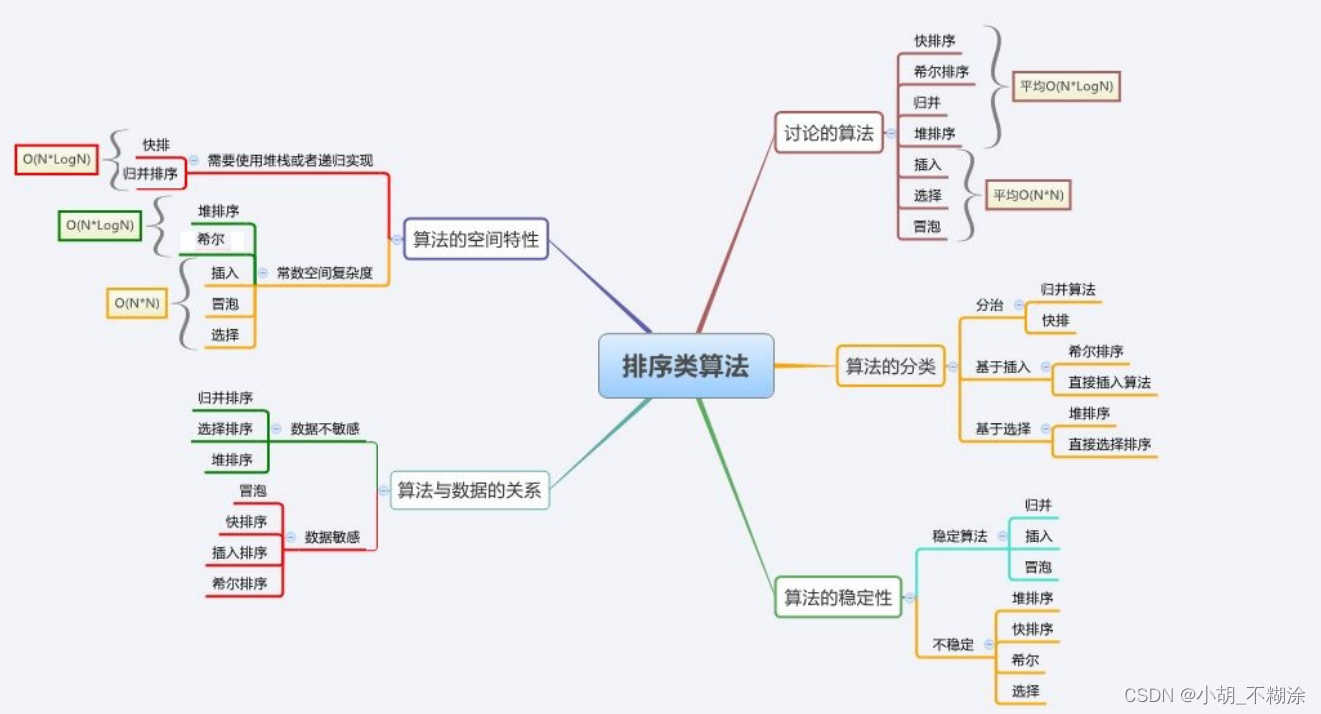
| 排序方法 | 最好 | 平均 | 最坏 | 空间复杂度 | 稳定性 |
|---|---|---|---|---|---|
| 冒泡排序 | O(n) | O(n^2) | O(n^2) | O(1) | 稳定 |
| 插入排序 | O(n) | O(n^2) | O(n^2) | O(1) | 稳定 |
| 选择排序 | O(n^2) | O(n^2) | O(n^2) | O(1) | 不稳定 |
| 希尔排序 | O(n) | O(n^1.3) | O(n^2) | O(1) | 不稳定 |
| 堆排序 | O(n * log(n)) | O(n * log(n)) | O(n * log(n)) | O(1) | 不稳定 |
| 快速排序 | O(n * log(n)) | O(n * log(n)) | O(n^2) | O(log(n)) ~ O(n) | 不稳定 |
| 归并排序 | O(n * log(n)) | O(n * log(n)) | O(n * log(n)) | O(n) | 稳定 |
相关文章:

【数据结构】排序算法总结
⭐ 作者:小胡_不糊涂 🌱 作者主页:小胡_不糊涂的个人主页 📀 收录专栏:浅谈数据结构 💖 持续更文,关注博主少走弯路,谢谢大家支持 💖 总结 1. 归并排序2. 计数排序3. 排序…...

作为20年老程序员,我如何使用GPT4来帮我写代码
如果你还在用google寻找解决代码bug的方案,那你真的out了,试试gpt4, save my life. 不是小编危言耸听,最近用gpt4来写代码极大地提高了代码生产力和运行效率,今天特地跟大家分享一下。 https://www.promptspower.comhttps://www.…...
【机器学习合集】模型设计之残差网络 ->(个人学习记录笔记)
文章目录 模型设计之残差网络1. 什么是残差结构1.1 网络加深遇到的优化问题1.2 short connect技术 2. 残差网络及有效性理解2.1 残差网络 3. 残差网络的发展3.1 密集残差网络3.2 更宽的残差网络(wide resnet)3.3 分组残差网络3.4 Dual Path Network3.5 加权残差网络3.6 预激活残…...

GoLong的学习之路(十六)基础工具之Gin框架
Gin框架介绍及使用,这张不用看内容就知道非常重要,重要到什么地步呢?重要到开发java不会Spring全家桶这种概念。 上几篇文章写的是如何构建骨架,经脉。这一章是将血肉注入。 文章目录 Gin框架RESTful API Gin渲染HTML渲染静态文件…...

VMware打开centos黑屏解决方法汇总
VMware打开centos黑屏解决方法汇总 前言:一. VMware打开centos黑屏解决方法汇总一 .情况情况一:情况二情况三 二. 解决方法最简单的方法:一. 以管理员权限在命令行执行1. 管理员身份运行cmd2. 输入“netsh winsock reset”,回车3. 重启电脑即…...

5G物联网关相较有线网关有哪些独特优势
5G为产业物联网应用带来了质的飞跃,5G技术实现更高速率、更低延迟和更大带宽,使得物联网能够接入更多数量的设备,实现更稳定、高效的连接和数据传输,在提高生产效率的同时,也进一步促进了物联网的应用发展和升级。 针对…...
【数据结构】顺序表的学习
前言:在之前我们学习了C语言的各种各样的语法,因此我们今天开始学习数据结构这一个模块,因此我们就从第一个部分来开始学习"顺序表"。 💖 博主CSDN主页:卫卫卫的个人主页 💞 👉 专栏分类:C程序设计谭浩强版本…...
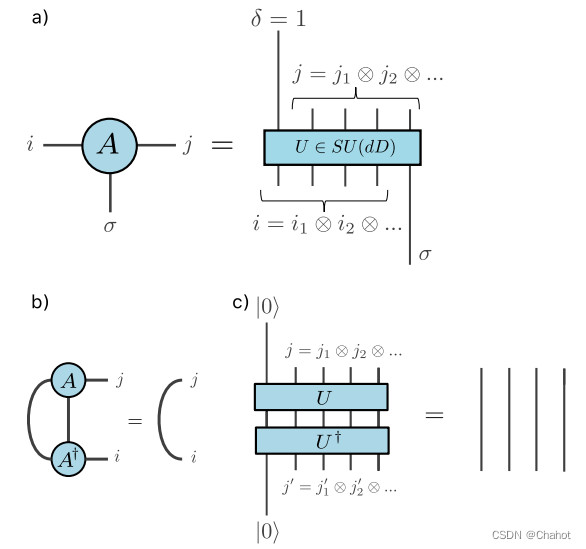
在NISQ小型计算机上执行大型并行量子计算的可能性
简介 Steve White提出了密度矩阵重整化群(DMRG)的基本思想,即纠缠是一种有价值的资源,可以用来精确或近似地描述大量子系统。后来,这一思想被理解为优化矩阵积状态(MPS)的算法,支持…...
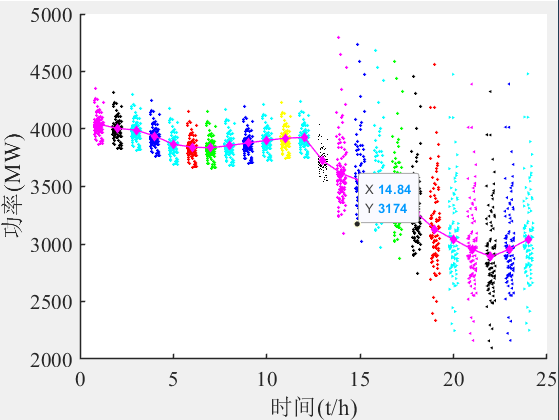
考虑时空相关性的风电功率预测误差MATLAB代码
微❤关注“电气仔推送”获得资料(专享优惠) 风电功率预测置信区间误差分析拟合 1.风电功率预测误差--时空相关性 展示第一一个时间段的风电功率预测与实际风电功率值的比较。填充区域表示预测的不确定性,显示了95%置信区间内预测可能的范围…...
ASP.NET WebApi 极简依赖注入
文章目录 环境服务类启动项注入使用依赖注入的优点 环境 .NET Core 7.0ASP.NET CoreVisual Studio 2022 服务类 public class T_TempService {public T_TempService(){}public void Test(){}}启动项注入 #region 依赖注入 builder.Services.AddTransient<T_TempService&g…...

解决proteus仿真stm32,IIC通讯,IIC DEBUG无法显示从机应答信号的问题(问题情况为在8位数据后应答位显示?)
1、错误现象 错误现象如下,在IIC数据传输8位数据后,IIC DEBUG的应答位无法显示应答位 2、错误原因 我们打开信号传输的示波器,直接去查看IIC从机校验位的数据波形,可以看到从机示波器显示的的波形为半高ACK,那错误原…...

PHP判断闰年
闰年的规则 1.能被4整除且不能被100整除 (普通闰年) 2.能被400整除,公历年份是整百数的,必须是400的倍数才是闰年(世纪闰年) 代码 function isLeapYear($year) {if($year%40 && $year%100!0){r…...

证照之星XE专业版下载专业证件照制作工具
值得肯定的是智能背景替换功能,轻松解决背景处理这一世界难题。不得不提及的是新增打印字体设置,包含字体选择、字号大小、字体颜色等。不同领域的应用证明了万能制作,系统支持自定义证照规格,并预设了17种常用的证件照规格。人所…...

VR全景图片如何制作?揭秘VR全景图片制作全流程
引言: VR全景图片是一种以全景视角为基础的图片制作技术,能够呈现出更为真实、立体的视觉体验。通过VR全景图片,观众可以360环顾四周,仿佛身临其境,提供了一种全新的感官体验,那么如何制作出令人满意的全景…...

vue element el-table-column 循环示例代码
如果你想循环生成多个el-table-column,可以使用v-for指令。以下是一个示例: <template><el-table :data"tableData"><el-table-column v-for"column in columns" :key"column.prop" :label"column.l…...
数据统计分析与绘图实践技术应用)
R语言生物群落(生态)数据统计分析与绘图实践技术应用
R 语言作的开源、自由、免费等特点使其广泛应用于生物群落数据统计分析。生物群落数据多样而复杂,涉及众多统计分析方法。以生物群落数据分析中的最常用的统计方法回归和混合效应模型、多元统计分析技术及结构方程等数量分析方法为主线,通过多个来自经典…...

有了 GPT,还需要付费咨询吗?
之前写过一篇文章《在创业公司,我靠它续命 …》,提到现在写代码基本靠 GPT。现在这种状况不仅没有改变,反而依赖更深。公司立项开发产品的 Linux 版本,全靠我一个人。我之前虽然一直使用 Linux 开发环境,对 Linux 系统…...

如何搭建一台服务器?
一.准备工作 1. 确定服务器类型:根据需求选择适合的服务器类型,如网站服务器、数据库服务器、文件服务器等。 2. 选择操作系统:根据服务器类型选择合适的操作系统,如Linux(如Ubuntu、CentOS)、Windows Se…...
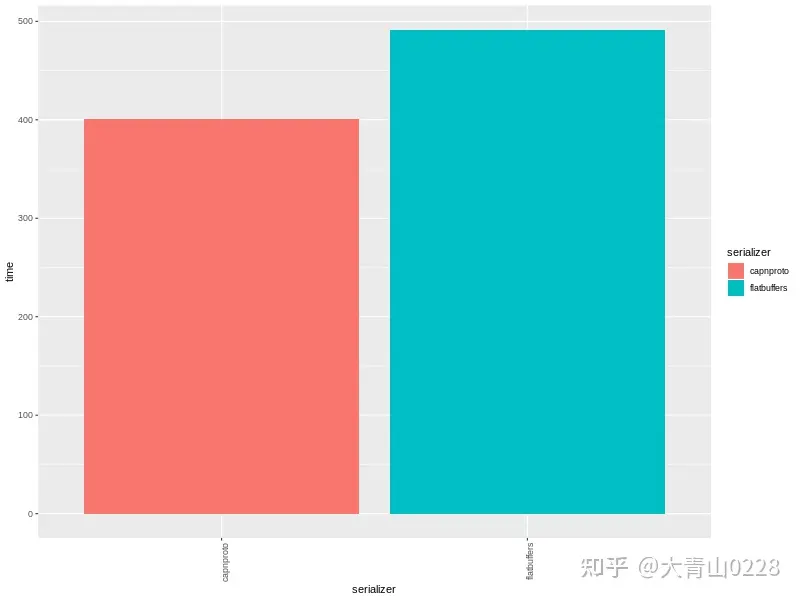
[转载]C++序列化框架介绍和对比
Google Protocol Buffers Protocol buffers 是一种语言中立,平台无关,可扩展的序列化数据的格式,可用于通信协议,数据存储等。 Protocol buffers 在序列化数据方面,它是灵活的,高效的。相比于 XML 来说&…...

分类预测 | Matlab实现KOA-CNN-BiLSTM-selfAttention多特征分类预测(自注意力机制)
分类预测 | Matlab实现KOA-CNN-BiLSTM-selfAttention多特征分类预测(自注意力机制) 目录 分类预测 | Matlab实现KOA-CNN-BiLSTM-selfAttention多特征分类预测(自注意力机制)分类效果基本描述程序设计参考资料 分类效果 基本描述 1…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

嵌入式学习笔记DAY33(网络编程——TCP)
一、网络架构 C/S (client/server 客户端/服务器):由客户端和服务器端两个部分组成。客户端通常是用户使用的应用程序,负责提供用户界面和交互逻辑 ,接收用户输入,向服务器发送请求,并展示服务…...
: 一刀斩断视频片头广告)
快刀集(1): 一刀斩断视频片头广告
一刀流:用一个简单脚本,秒杀视频片头广告,还你清爽观影体验。 1. 引子 作为一个爱生活、爱学习、爱收藏高清资源的老码农,平时写代码之余看看电影、补补片,是再正常不过的事。 电影嘛,要沉浸,…...

基于Java+VUE+MariaDB实现(Web)仿小米商城
仿小米商城 环境安装 nodejs maven JDK11 运行 mvn clean install -DskipTestscd adminmvn spring-boot:runcd ../webmvn spring-boot:runcd ../xiaomi-store-admin-vuenpm installnpm run servecd ../xiaomi-store-vuenpm installnpm run serve 注意:运行前…...

webpack面试题
面试题:webpack介绍和简单使用 一、webpack(模块化打包工具)1. webpack是把项目当作一个整体,通过给定的一个主文件,webpack将从这个主文件开始找到你项目当中的所有依赖文件,使用loaders来处理它们&#x…...