509. 斐波那契数
斐波那契数 (通常用 F(n) 表示)形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始,后面的每一项数字都是前面两项数字的和。也就是:
F(0) = 0,F(1) = 1 F(n) = F(n - 1) + F(n - 2),其中 n > 1
给定 n ,请计算 F(n) 。
示例 1:
输入:n = 2 输出:1 解释:F(2) = F(1) + F(0) = 1 + 0 = 1
示例 2:
输入:n = 3 输出:2 解释:F(3) = F(2) + F(1) = 1 + 1 = 2
示例 3:
输入:n = 4 输出:3 解释:F(4) = F(3) + F(2) = 2 + 1 = 3
提示:
0 <= n <= 30
class Solution {
public:int fib(int n) {//定义dp数组的意思//状态//初始化//遍历顺序//dp数组值是否符合if(n < 2) return n;// 表示第一个斐波那契数为dp[i];vector<int>dp(n+1); // 因为下面直接访问dp[0]和dp[1],所以得先加内存。dp[0] = 0;dp[1] = 1;for(int i = 2;i <= n;i++){dp[i] = dp[i-1]+dp[i-2];}return dp[n];}
};相关文章:

509. 斐波那契数
斐波那契数 (通常用 F(n) 表示)形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始,后面的每一项数字都是前面两项数字的和。也就是: F(0) 0,F(1) 1 F(n) F(n - 1) F(n - 2),其中 n > 1给定 n &a…...

四、[mysql]索引优化-1
目录 前言一、场景举例1.联合索引第一个字段用范围查询不走索引(分情况)2.强制走指定索引3.覆盖索引优化4.in和or在表数据量比较大的情况会走索引,在表记录不多的情况下会选择全表扫描5.like 后% 一般情况都会走索引(索引下推) 二、Mysql如何选择合适的索…...
:神经网络-最大池化使用)
PyTorch入门学习(九):神经网络-最大池化使用
目录 一、数据准备 二、创建神经网络模型 三、可视化最大池化效果 一、数据准备 首先,需要准备一个数据集来演示最大池化层的应用。在本例中,使用了CIFAR-10数据集,这是一个包含10个不同类别图像的数据集,用于分类任务。我们使…...
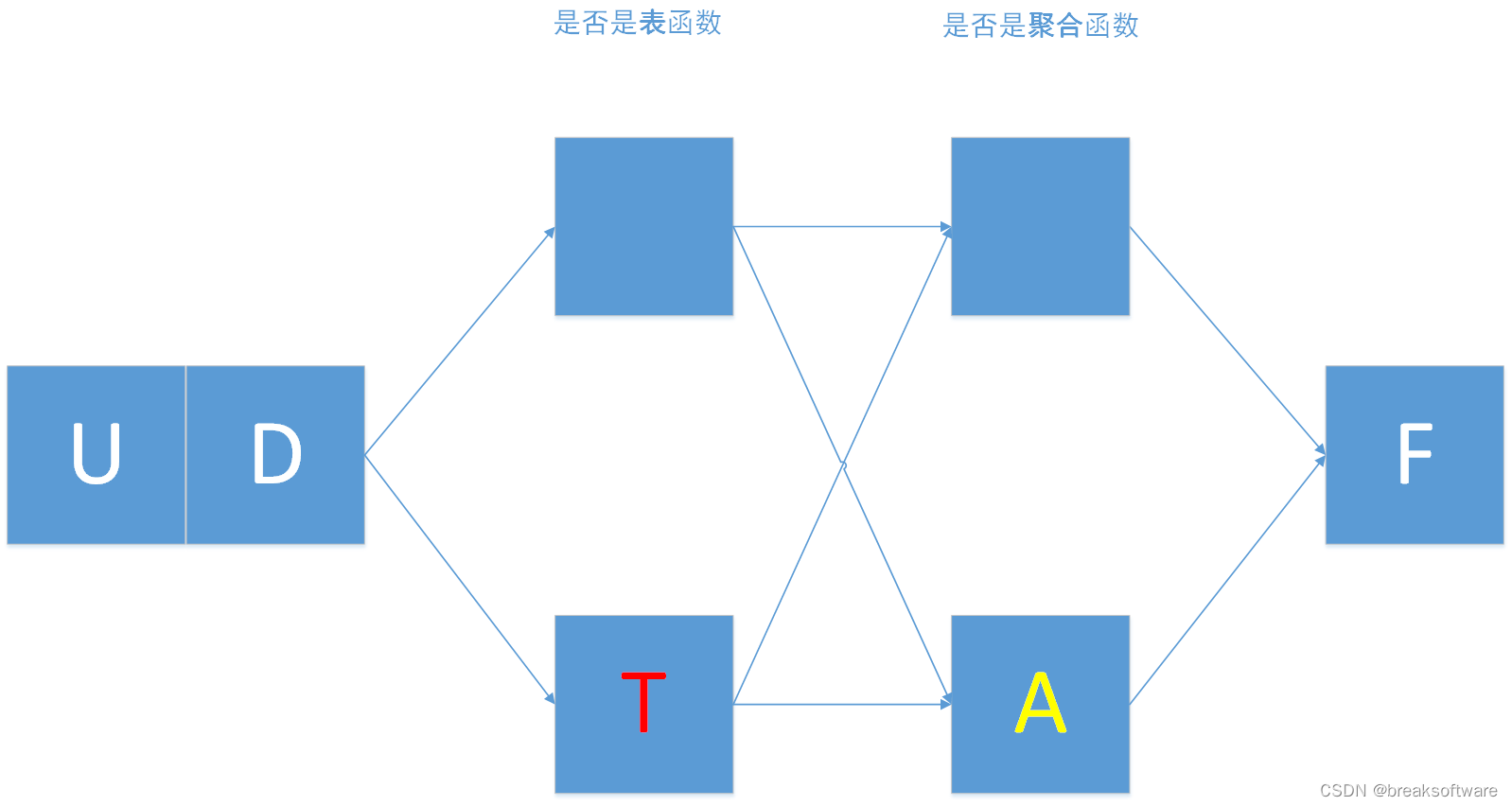
0基础学习PyFlink——用户自定义函数之UDF
大纲 标量函数入参并非表中一行(Row)入参是表中一行(Row)alias PyFlink中关于用户定义方法有: UDF:用户自定义函数。UDTF:用户自定义表值函数。UDAF:用户自定义聚合函数。UDTAF&…...

英语小作文模板(06求助+描述;07描述+建议)
06 求助描述: 题目背景及要求 第一段 第二段 第三段 翻译成中文 07 描述+建议: 题目背景及要求 第一段 第二段...

为什么感觉假期有时候比上班还累?
假期比上班还累的感觉可能由以下几个原因造成: 计划过度:在假期里,人们往往会制定各种计划,如旅游、聚会、休息等,以充分利用这段时间。然而,如果这些计划过于紧张或安排得过于紧密,就会导致身…...
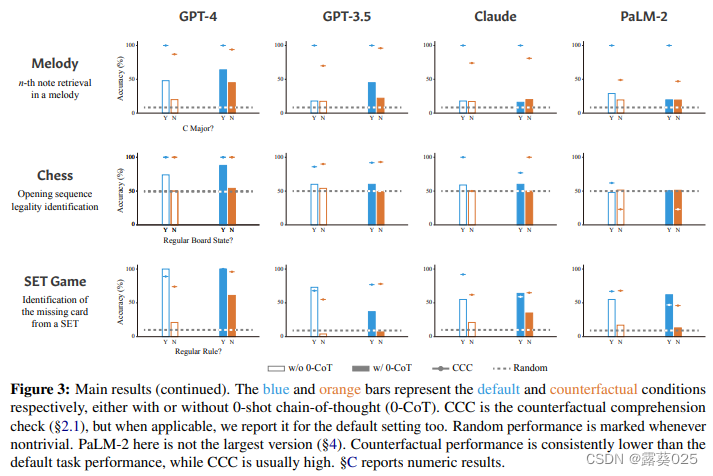
推理还是背诵?通过反事实任务探索语言模型的能力和局限性
推理还是背诵?通过反事实任务探索语言模型的能力和局限性 摘要1 引言2 反事实任务2.1 反事实理解检测 3 任务3.1 算术3.2 编程3.3 基本的句法推理3.4 带有一阶逻辑的自然语言推理3.5 空间推理3.6 绘图3.7 音乐3.8 国际象棋 4 结果5 分析5.1 反事实条件的“普遍性”5…...
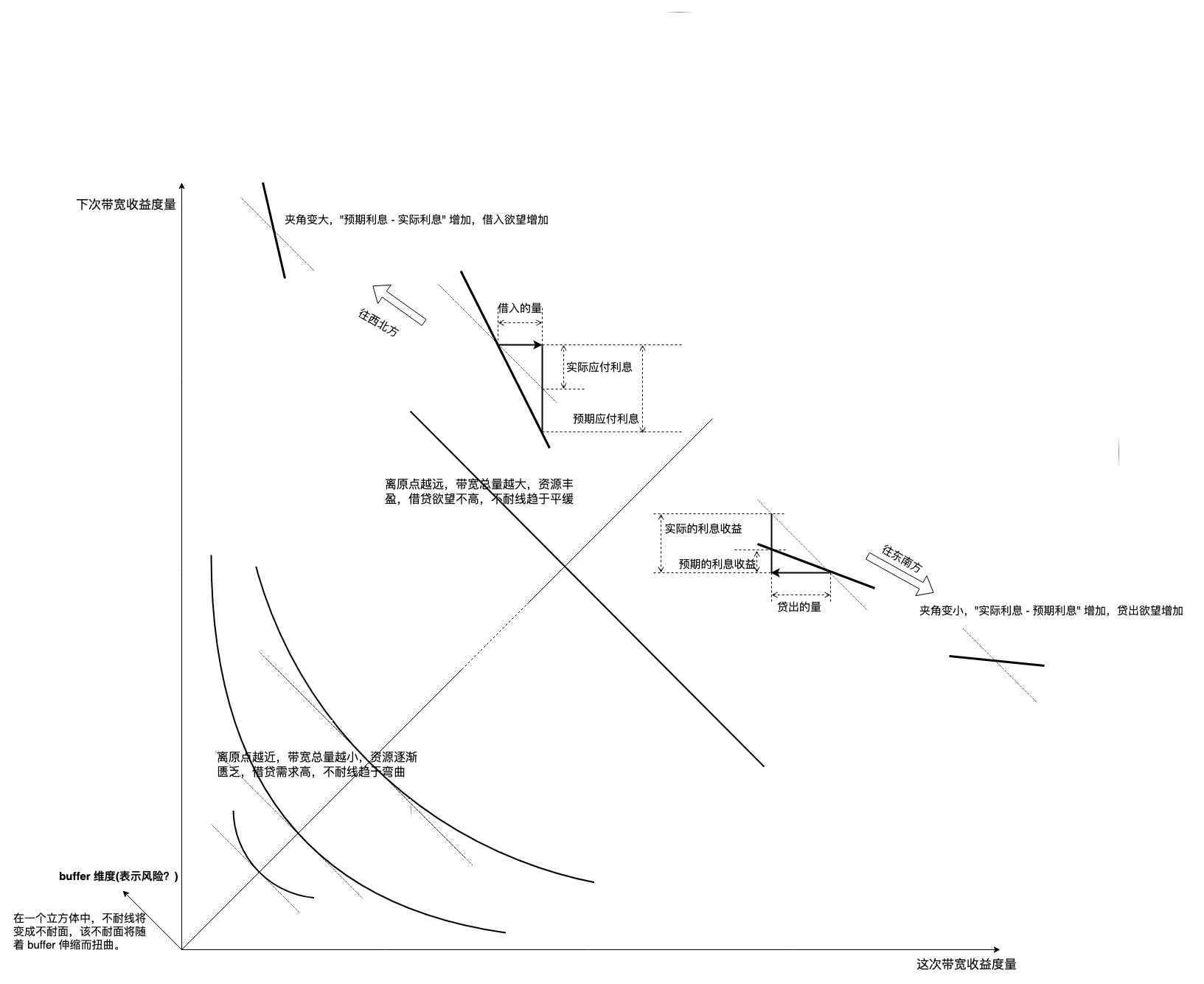
《利息理论》指导 TCP 拥塞控制
欧文费雪《利息原理》第 10 章,第 11 章对利息的几何说明是普适的,任何一个负反馈系统都能引申出新结论。给出原书图示,本文依据于此,详情参考原书: 将 burst 看作借贷是合理的,它包含成本(报文)…...
)
Bsdiff,Bspatch 的差分增量升级(基于Win和Linux)
目录 背景 内容 准备工作 在windows平台上 在linux平台上 正式工作 生成差分文件思路 作用差分文件思路 在保持相同目录结构进行差分增量升级 服务端(生成差分文件) 客户端(作用差分文件) 背景 像常见的Android 的linux平台,游戏,系统更新都…...

【3妹教我学历史-秦朝史】2 秦穆公-韩原之战
插: 前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。点击跳转到网站。 坚持不懈,越努力越幸运,大家一起学习鸭~~~ 3妹:2哥,今天下班这么早&#…...

车载控制器
文章目录 车载控制器电动汽车上都有什么ECU 车载控制器 智能汽车上的控制器数量因车型和制造商而异。一般来说,现代汽车可能有50到100个电子控制单元(ECU)或控制器。这些控制器负责管理各种系统,如发动机管理、刹车、转向、空调、…...
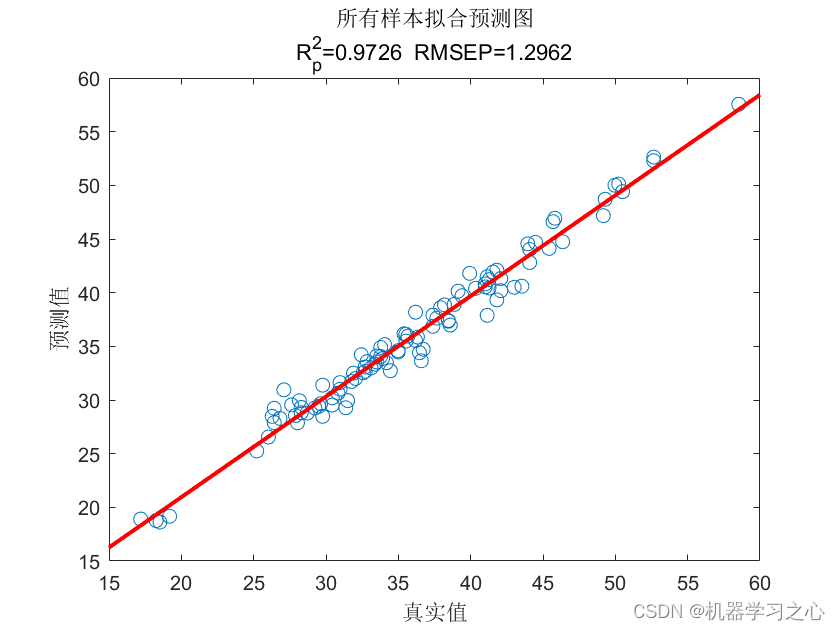
回归预测 | Matlab实现RIME-CNN-SVM霜冰优化算法优化卷积神经网络-支持向量机的多变量回归预测
回归预测 | Matlab实现RIME-CNN-SVM霜冰优化算法优化卷积神经网络-支持向量机的多变量回归预测 目录 回归预测 | Matlab实现RIME-CNN-SVM霜冰优化算法优化卷积神经网络-支持向量机的多变量回归预测效果一览基本介绍程序设计参考资料 效果一览 基本介绍 1.RIME-CNN-SVM霜冰优化算…...

使用Jaeger进行分布式跟踪:学习如何在服务网格中使用Jaeger来监控和分析请求的跟踪信息
🌷🍁 博主猫头虎 带您 Go to New World.✨🍁 🦄 博客首页——猫头虎的博客🎐 🐳《面试题大全专栏》 文章图文并茂🦕生动形象🦖简单易学!欢迎大家来踩踩~🌺 &a…...

添加多个单元对象
开发环境: Windows 11 家庭中文版Microsoft Visual Studio Community 2019VTK-9.3.0.rc0vtk-example参考代码 demo解决问题:不同阶段添加多个单元对象。 定义一个点集和一个单元集合,单元的类型可以是点、三角形、矩形、多边形等基本图形。只…...
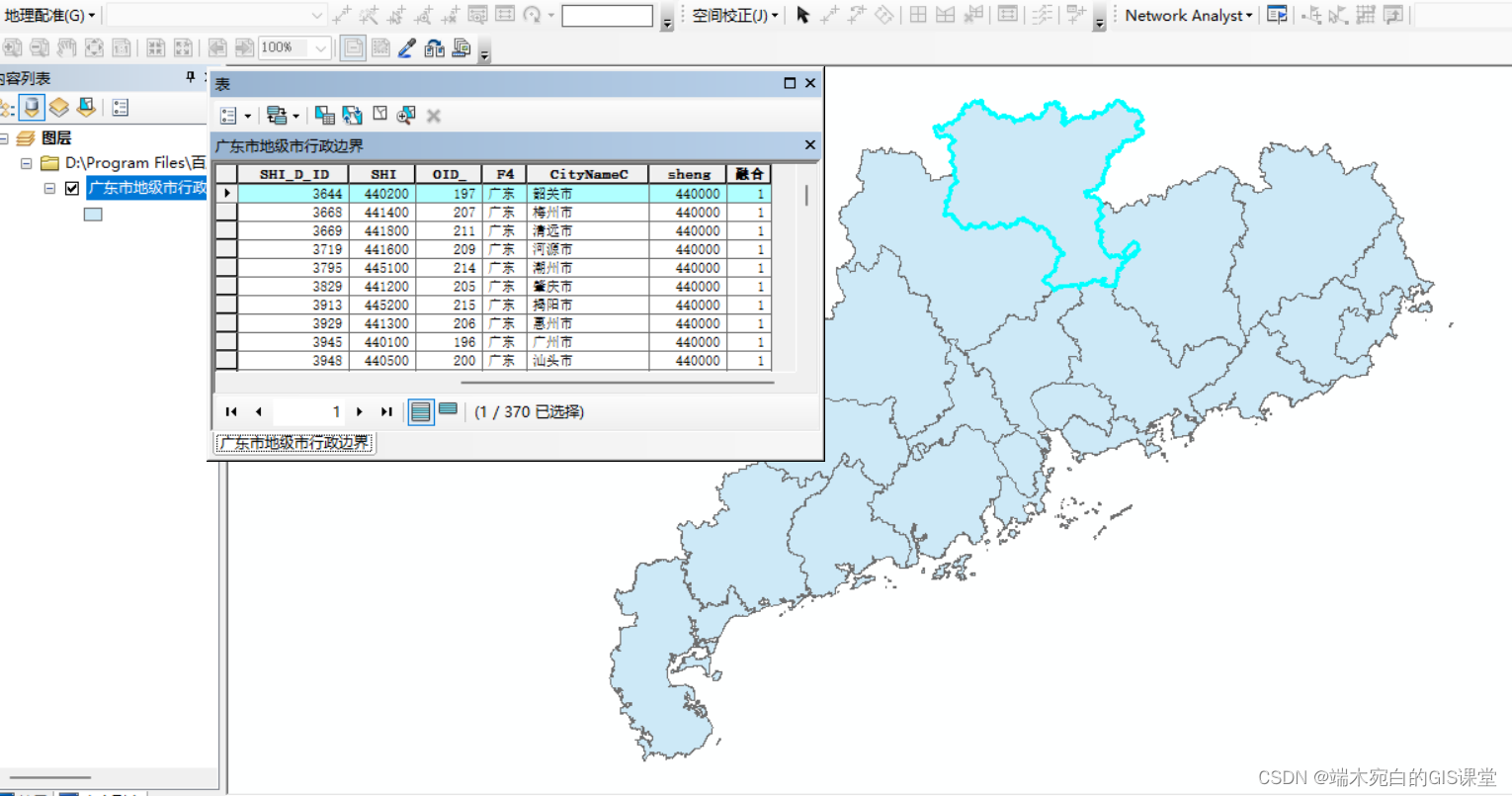
十八、模型构建器(ModelBuilder)快速提取城市建成区——批量掩膜提取夜光数据、夜光数据转面、面数据融合、要素转Excel(基于参考比较法)
一、前言 前文实现批量投影栅格、转为整型,接下来重点实现批量提取夜光数据,夜光数据转面、夜光数据面数据融合、要素转Excel。将相关结果转为Excel,接下来就是在Excel中进行阈值的确定,阈值确定无法通过批量操作,除非采用其他方式,但是那样的学习成本较高,对于参考比较…...

HarmonyOS开发:基于http开源一个网络请求库
前言 网络封装的目的,在于简洁,使用起来更加的方便,也易于我们进行相关动作的设置,如果,我们不封装,那么每次请求,就会重复大量的代码逻辑,如下代码,是官方给出的案例&am…...
【杂记】Ubuntu20.04装系统,安装CUDA等
装20.04系统 安装系统的过程中,ROG的B660G主板,即使不关掉Secure boot也是可以的,不会影响正常安装,我这边出现问题的主要原因是使用了Ventoy制作的系统安装盘,导致每次一选择使用U盘的UEFI启动,就会跳回到…...

040-第三代软件开发-全新波形抓取算法
第三代软件开发-全新波形抓取算法 文章目录 第三代软件开发-全新波形抓取算法项目介绍全新波形抓取算法代码小解 关键字: Qt、 Qml、 抓波、 截获、 波形 项目介绍 欢迎来到我们的 QML & C 项目!这个项目结合了 QML(Qt Meta-Object …...
分享一个基于asp.net的供销社农产品商品销售系统的设计与实现(源码调试 lw开题报告ppt)
💕💕作者:计算机源码社 💕💕个人简介:本人七年开发经验,擅长Java、Python、PHP、.NET、微信小程序、爬虫、大数据等,大家有这一块的问题可以一起交流! 💕&…...
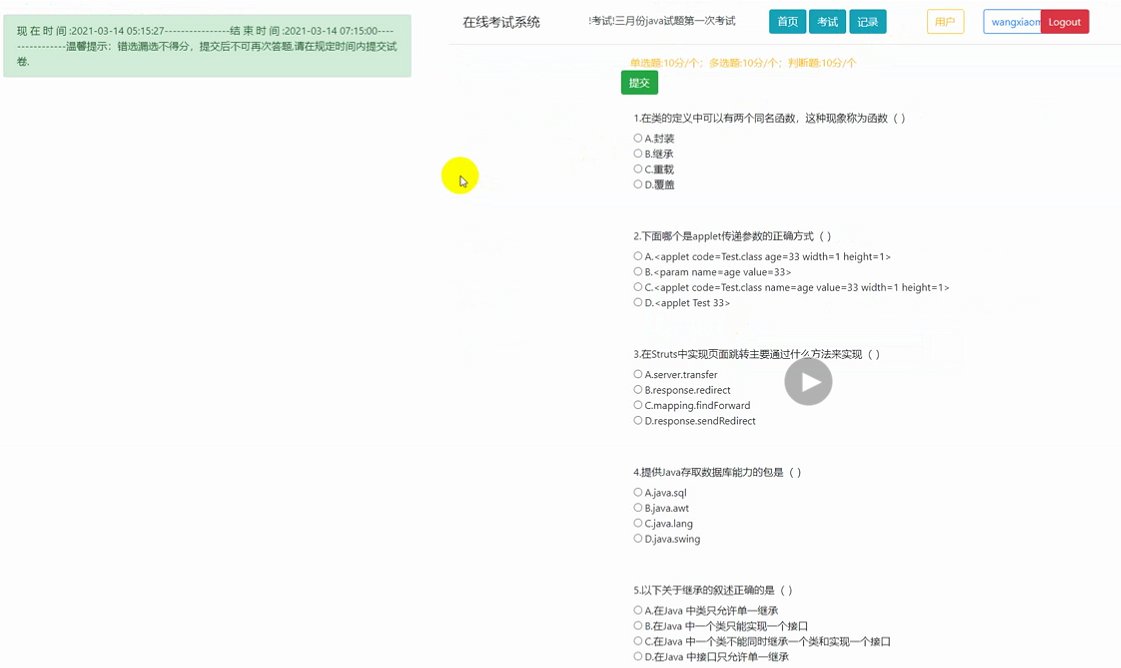
Java基于SpringBoot的线上考试系统
1 摘 要 基于 SpringBoot 的在线考试系统网站,功能模块具有课程管理、成绩管理、教师管理、学生管理、考试管理以及基本信息的管理等,通过将系统分为管理员、授课教师以及学生,从不同的身份角度来对用户提供便利,将科技与教学模式…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...

#Uniapp篇:chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器:Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...

面向无人机海岸带生态系统监测的语义分割基准数据集
描述:海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而,目前该领域仍面临一个挑战,即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...

MySQL JOIN 表过多的优化思路
当 MySQL 查询涉及大量表 JOIN 时,性能会显著下降。以下是优化思路和简易实现方法: 一、核心优化思路 减少 JOIN 数量 数据冗余:添加必要的冗余字段(如订单表直接存储用户名)合并表:将频繁关联的小表合并成…...

【安全篇】金刚不坏之身:整合 Spring Security + JWT 实现无状态认证与授权
摘要 本文是《Spring Boot 实战派》系列的第四篇。我们将直面所有 Web 应用都无法回避的核心问题:安全。文章将详细阐述认证(Authentication) 与授权(Authorization的核心概念,对比传统 Session-Cookie 与现代 JWT(JS…...
 ----- Python的类与对象)
Python学习(8) ----- Python的类与对象
Python 中的类(Class)与对象(Object)是面向对象编程(OOP)的核心。我们可以通过“类是模板,对象是实例”来理解它们的关系。 🧱 一句话理解: 类就像“图纸”,对…...
