LeetCode:2003. 每棵子树内缺失的最小基因值(C++)
目录
2003. 每棵子树内缺失的最小基因值
题目描述:
实现代码与解析:
dfs + 启发式合并
原理思路:
2003. 每棵子树内缺失的最小基因值
题目描述:
有一棵根节点为 0 的 家族树 ,总共包含 n 个节点,节点编号为 0 到 n - 1 。给你一个下标从 0 开始的整数数组 parents ,其中 parents[i] 是节点 i 的父节点。由于节点 0 是 根 ,所以 parents[0] == -1 。
总共有 105 个基因值,每个基因值都用 闭区间 [1, 105] 中的一个整数表示。给你一个下标从 0 开始的整数数组 nums ,其中 nums[i] 是节点 i 的基因值,且基因值 互不相同 。
请你返回一个数组 ans ,长度为 n ,其中 ans[i] 是以节点 i 为根的子树内 缺失 的 最小 基因值。
节点 x 为根的 子树 包含节点 x 和它所有的 后代 节点。
示例 1:

输入:parents = [-1,0,0,2], nums = [1,2,3,4] 输出:[5,1,1,1] 解释:每个子树答案计算结果如下: - 0:子树包含节点 [0,1,2,3] ,基因值分别为 [1,2,3,4] 。5 是缺失的最小基因值。 - 1:子树只包含节点 1 ,基因值为 2 。1 是缺失的最小基因值。 - 2:子树包含节点 [2,3] ,基因值分别为 [3,4] 。1 是缺失的最小基因值。 - 3:子树只包含节点 3 ,基因值为 4 。1是缺失的最小基因值。
示例 2:
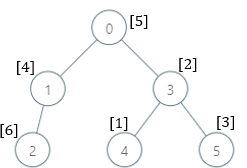
输入:parents = [-1,0,1,0,3,3], nums = [5,4,6,2,1,3] 输出:[7,1,1,4,2,1] 解释:每个子树答案计算结果如下: - 0:子树内包含节点 [0,1,2,3,4,5] ,基因值分别为 [5,4,6,2,1,3] 。7 是缺失的最小基因值。 - 1:子树内包含节点 [1,2] ,基因值分别为 [4,6] 。 1 是缺失的最小基因值。 - 2:子树内只包含节点 2 ,基因值为 6 。1 是缺失的最小基因值。 - 3:子树内包含节点 [3,4,5] ,基因值分别为 [2,1,3] 。4 是缺失的最小基因值。 - 4:子树内只包含节点 4 ,基因值为 1 。2 是缺失的最小基因值。 - 5:子树内只包含节点 5 ,基因值为 3 。1 是缺失的最小基因值。
示例 3:
输入:parents = [-1,2,3,0,2,4,1], nums = [2,3,4,5,6,7,8] 输出:[1,1,1,1,1,1,1] 解释:所有子树都缺失基因值 1 。
提示:
n == parents.length == nums.length2 <= n <= 105- 对于
i != 0,满足0 <= parents[i] <= n - 1 parents[0] == -1parents表示一棵合法的树。1 <= nums[i] <= 105nums[i]互不相同。
实现代码与解析:
dfs + 启发式合并
class Solution {
public:// 邻接表vector<int> h = vector<int>(1e5 + 10, -1); vector<int> e = vector<int>(1e5 + 10, 0); vector<int> ne = vector<int>(1e5 + 10, 0);int idx = 0;void add(int a, int b) {e[idx] = b, ne[idx] = h[a], h[a] = idx++;}vector<int> smallestMissingValueSubtree(vector<int>& parents, vector<int>& nums) {int n = parents.size();// 存图 加边 邻接表for (int i = 1; i < n; i++) { // 这里从1开始,找半天错。。add(parents[i], i);}vector<int> res(n, 1); // 结果数组vector<unordered_set<int>> gene(n); // 包含此节点 与 其子树 的基因合集setfunction<int(int)> dfs = [&](int cur) -> int{gene[cur].insert(nums[cur]); // 当前节点基因值放入for (int i = h[cur]; ~i; i = ne[i]) {int j = e[i]; // 子节点res[cur] = max(res[cur], dfs(j)); // 此节点为根缺失的最小的基因,一定比子树缺失的最小基因大或等于,所以这里取个max// 向上传递合集,小的合并到大的效率快,所以先判断(选择是否先交换),在树中属于中序处理if (gene[cur].size() < gene[j].size()) {gene[cur].swap(gene[j]);}gene[cur].merge(gene[j]); // 合并}// 根据res寻找此节点的结果, 一定比子树大或等于,++遍历即可,找到第一个没有的最小基因while (gene[cur].count(res[cur]) > 0) {res[cur]++;}return res[cur];};dfs(0); // dfsreturn res;}
};原理思路:
vector<unordered_set<int>> gene(n); // 包含此节点 与 其子树 的基因合集set
dfs返回此节点的结果(缺失基因最小值),递归向上处理,每次将子树的集合与其根节点集合合并,根节点的缺失最小值一定大于等于其子树。从最大子树缺失的最小基因开始++遍历,找到第一个不在集合中的值,就为以此节点为根的树的缺失的最小基因。
此题的核心,就是我们不仅要向上传递子树缺失的最小基因,还要根据树中包含的节点来找出缺失基因,所以每个节点多了set来记录以它为根的树包含的节点,每次向上来合并set是此题的关键。
相关文章:

LeetCode:2003. 每棵子树内缺失的最小基因值(C++)
目录 2003. 每棵子树内缺失的最小基因值 题目描述: 实现代码与解析: dfs 启发式合并 原理思路: 2003. 每棵子树内缺失的最小基因值 题目描述: 有一棵根节点为 0 的 家族树 ,总共包含 n 个节点,节点编…...

React Hooks之useContext使用
官方文档写道:在组件的顶层调用 useContext 来读取和订阅 context。 我理解就是一个“全局变量”的概念。它可以用来声明一个变量,然后在各个组件中使用,避免了props一级一级往下传,当然使用场景有限,比如设置一个主题…...
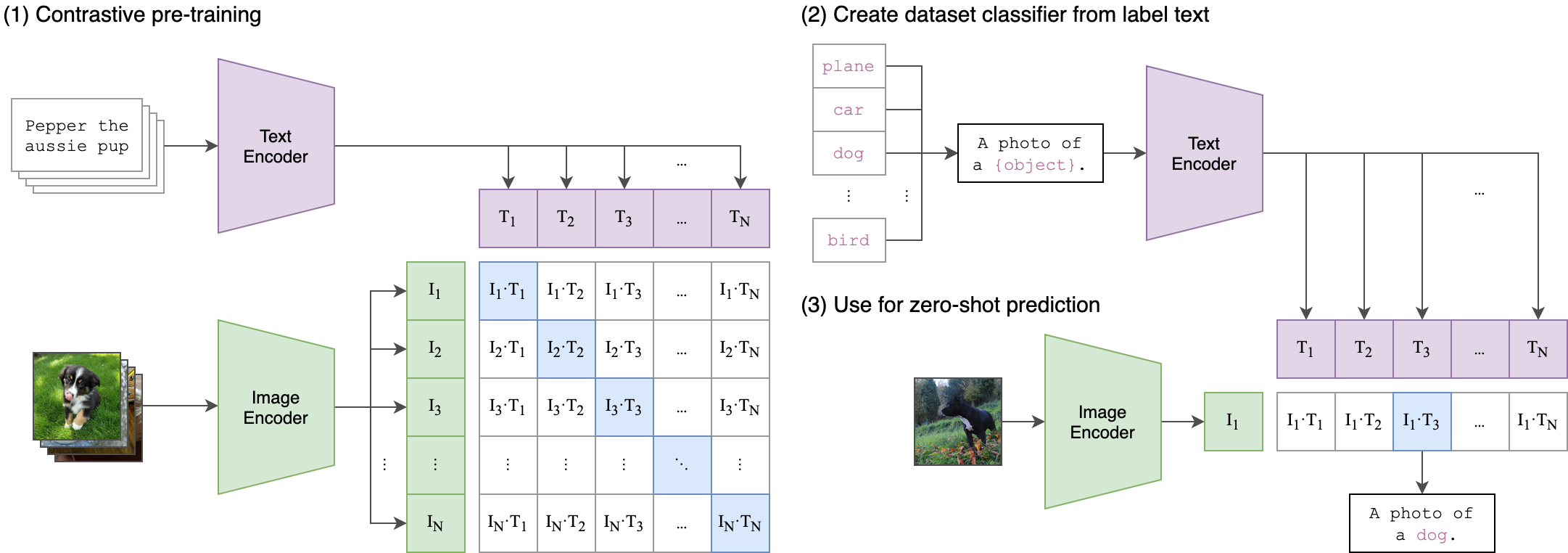
多模态对比语言图像预训练CLIP:打破语言与视觉的界限
项目设计集合(人工智能方向):助力新人快速实战掌握技能、自主完成项目设计升级,提升自身的硬实力(不仅限NLP、知识图谱、计算机视觉等领域):汇总有意义的项目设计集合,助力新人快速实…...

使用s3cmd访问S3存储 -【真实案例】
背景 项目中使用到了 S3 存储(基于华为云 OBS),并且在应用服务器上开通了到 S3 存储的防火墙。 👉 目标:在应用服务器上验证 S3 存储是否通畅可用。 👉 选型:经过分析,发现在 Linux 下可以使用 s3cmd 来访问 S3 存储。 s3cmd 简介 s3cmd 是一个开源免费的、基于 P…...
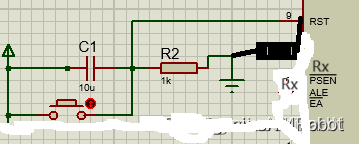
51单片机复位电容计算与分析(附带Proteus电路图)
因为iC x (dU/dt).在上电瞬间,U从0变化到U,所以这一瞬间就是通的,然后这就是一个直流回路,因为电容C直流中是断路的,所以就不通了。 然后来分析一下这个电容的电压到底是能不能达到单片机需要的复位电压。 这是一个线性电容&…...

前端性能瓶颈崩溃项目?Webpack助力解决!
🎬 江城开朗的豌豆:个人主页 🔥 个人专栏 :《 VUE 》 《 javaScript 》 📝 个人网站 :《 江城开朗的豌豆🫛 》 ⛺️ 生活的理想,就是为了理想的生活 ! 目录 ⭐ 专栏简介 📘 文章引言 一、背…...

纷享销客BI,助力企业激活数据价值,科学企业决策
10月25日上午,国家数据局正式挂牌成立,这标志着我国数字经济发展将进入新的发展阶段,也将有力促进数据要素技术创新、开发利用和有效治理,以数据强国支撑数字中国的建设。伴随数据作为企业新的生产要素的意义不断凸显,…...
SpringBoot整合阿里云OSS对象存储
文章目录 1、OSS介绍及开通1.1、阿里云OSS简介1.2、开通OSS 2、创建存储空间bucket及密钥获取2.1、创建存储空间2.2、获取密钥 3、OSS快速入门案例4、在springboot项目中整合4.1、将oss配置放到yml文件中4.2、创建Oss属性类,接收yml文件中的属性4.3、封装文件上传功…...
【ES专题】ElasticSearch快速入门
目录 前言从一个【搜索】说起 阅读对象阅读导航笔记正文一、全文检索1.1 什么是【全文检索】1.2 【全文检索】原理1.3 什么是倒排索引 二、ElasticSearch简介2.1 ElasticSearch介绍2.2 ElasticSearch应用场景2.3 数据库横向对比 三、ElasticSearch环境搭建3.1 Windows下安装3.2…...

案例分析真题-质量属性
案例分析真题-质量属性 2009 年真题 【问题1】 【问题2】 2011 年真题 【问题1】 骚戴理解:首先要知道这样的题目没有可靠性,只有可用性,更没有容错性,这里我(3)写成了i,而不是f,仔…...

微信小程序面试题之理论篇
本文内容,来源于极客学院的分享,这里只做引用。 说说你对微信小程序的理解?优缺点? 背景 小程序与H5 优缺点 优点:缺点: 说说微信小程序的生命周期函数有哪些? 应用的生命周期页面的生命期组件的生命周期执行过程 应…...

C++前缀和算法的应用:统计上升四元组
C前缀和算法的应用:统计上升四元组 本文涉及的基础知识点 C算法:前缀和、前缀乘积、前缀异或的原理、源码及测试用例 包括课程视频 题目 给你一个长度为 n 下标从 0 开始的整数数组 nums ,它包含 1 到 n 的所有数字,请你返回上…...

华泰证券:新奥能源:零售气待恢复,泛能与智家仍是亮点
来源:猛兽财经 作者:猛兽财经 猛兽财经获悉,由于新奥能源(02688)发布三季度经营数据: 1-3Q23:天然气零售量yoy-4.7%,燃气批发量yoy17.6%,综合能源销量yoy34.2%ÿ…...
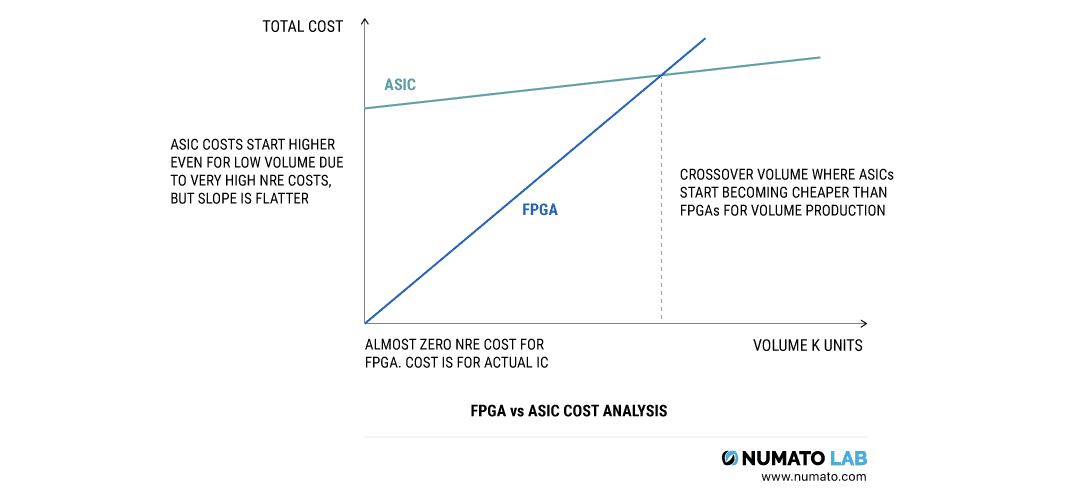
FPGA与ASIC有什么差异?二者该如何选用?
前言 对于一个数字电路的新手来说,这可能是会经常遇到的一个问题:FPGA和ASIC之间的区别是什么? 接下来本文将尝试讲解 “什么是FPGA?” 和 “什么是ASIC?”,然后讲述一些关于FPGA和ASIC的问题,例如它们之间…...

Kotlin run 用法
Kotlin 中的 .run 函数可以用于不同的场景,下面是一些常见的用法: 执行代码块并返回结果: val result run {// 在这里编写一些代码逻辑// 返回最后一个表达式的结果"Hello, Kotlin" }println(result) // 输出:Hello, …...
iZotope RX 10(音频修复和增强工具)
iZotope RX 10是一款音频修复和增强软件,主要特点包括: 声音修复:iZotope RX 10可以去除不良噪音、杂音、吱吱声等,使音频变得更加清晰干净。音频增强:iZotope RX 10支持对音频进行音量调节、均衡器、压缩器、限制器等…...
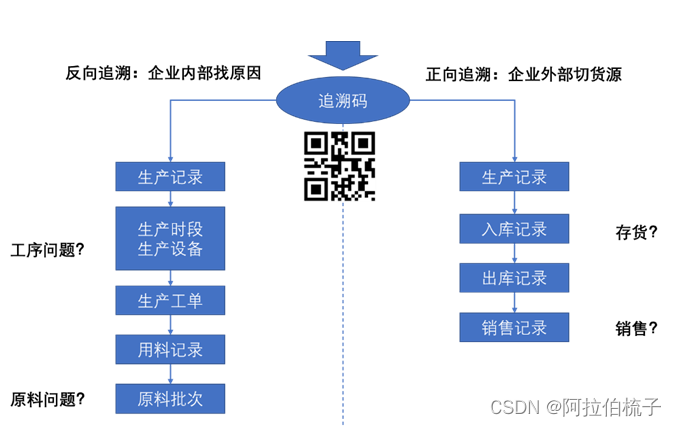
MES 价值点之数据追随
在现代制造业中,数据追溯已经越来越得到重视,特别是那些推行精益生产的企业重要性就更加突出了,而制造执行系统(MES)作为一种关键的生产管理工具,是能很好的为制造企业提供数据追溯功能。今天,和…...

yolo8制作自己的数据集训练和预测分割
一、训练coco128-seg数据集,增加一个类别 coco128-seg数据集下载: github链接 csdn链接 1、修改两个配置文件 (1)、修改"E:\python\ultralytics-main\ultralytics\cfg\datasets\coco128-seg.yaml"路径下的coco128-seg.yaml数据集配置文件,可以拷贝出来 修改数…...
分享一下怎么做一个同城配送小程序
如何制作一个同城配送小程序:功能特点、使用指南及未来展望 一、引言 随着互联网的快速发展,人们对于生活服务的需求越来越高。同城配送作为连接消费者与商家的桥梁,越来越受到人们的关注。本文将详细介绍如何制作一个同城配送小程序&#…...
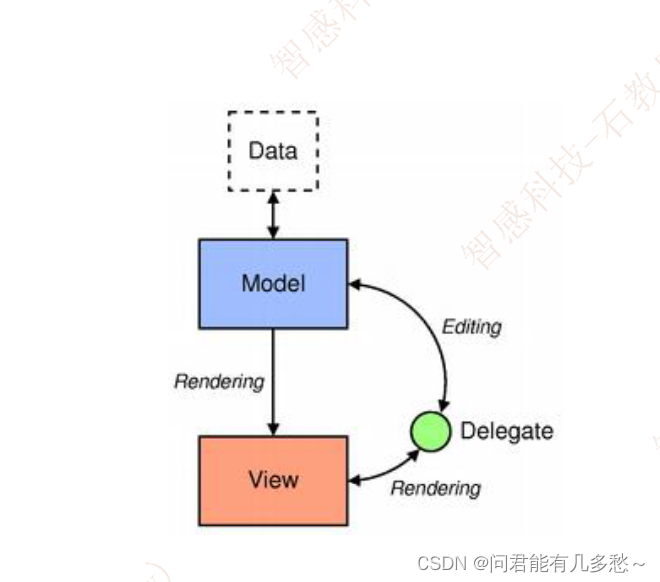
Qt 中model/View 架构 详解,以及案例实现相薄功能
model/View 架构 导读 我们的系统需要显示大量数据,比如从数据库中读取数据,以自己的方式显示在自己的应用程序的界面中。早期的 Qt 要实现这个功能,需要定义一个组件,在这个组件中保存一个数据对象,比如一个列表。我们对这个列表进行查找、插入等的操作,或者把修改…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...
