拓展卡尔曼滤波EKF
How to fusion two Gauss Distribution
N ( x , μ 0 , σ 0 ) N ( x , μ 1 , σ 1 ) = N ( x , μ ′ , σ ′ ) \begin{equation} \begin{aligned} \mathcal{N}(x,\mu_0,\sigma_0) \mathcal{N}(x,\mu_1,\sigma_1) = \mathcal{N}(x,\mu',\sigma') \\ \end{aligned} \end{equation} N(x,μ0,σ0)N(x,μ1,σ1)=N(x,μ′,σ′)
μ ′ = μ 0 σ 1 2 + μ 1 σ 0 2 σ 0 2 + σ 1 2 = μ 0 + σ 0 2 ( μ 1 − μ 0 ) σ 0 2 + σ 1 2 σ ′ = σ 0 2 σ 1 2 σ 0 2 + σ 1 2 = σ 0 2 − σ 0 4 σ 0 2 + σ 1 2 \begin{equation} \begin{aligned} \mu' &= \frac{\mu_0\sigma_1^2 + \mu_1\sigma_0^2}{\sigma_0^2 + \sigma_1^2} = \mu_0 + \frac{\sigma_0^2 (\mu_1 - \mu_0)}{\sigma_0^2 + \sigma_1^2} \\ \sigma' &= \frac{\sigma_0^2 \sigma_1^2}{\sigma_0^2 + \sigma_1^2} = \sigma_0^2 - \frac{\sigma_0^4}{\sigma_0^2 + \sigma_1^2} \\ \end{aligned} \end{equation} μ′σ′=σ02+σ12μ0σ12+μ1σ02=μ0+σ02+σ12σ02(μ1−μ0)=σ02+σ12σ02σ12=σ02−σ02+σ12σ04
k = σ 0 2 σ 0 1 + σ 1 2 μ ′ = μ 0 + k ( μ 1 − μ 0 ) σ ′ = σ 0 2 − k σ 0 2 \begin{equation} \begin{aligned} k &= \frac{\sigma_0^2}{\sigma_0^1 + \sigma_1^2} \\ \mu' &= \mu_0 + k(\mu_1 - \mu_0) \\ \sigma' &= \sigma_0^2 - k\sigma_0^2 \\ \end{aligned} \end{equation} kμ′σ′=σ01+σ12σ02=μ0+k(μ1−μ0)=σ02−kσ02
EFK
根据建模预测:
x ^ k = F k x k − 1 + B k u k P ^ k = F k P k − 1 F k T + Q k \begin{equation} \begin{aligned} \hat{x}_k = F_k x_{k-1} + B_k u_k \\ \hat{P}_k = F_k P_{k-1}F_k^T + Q_k \\ \end{aligned} \end{equation} x^k=Fkxk−1+BkukP^k=FkPk−1FkT+Qk
将预测转到测量空间:
( μ 0 , Σ 0 ) = ( H k x ^ k , H k P ^ k H k T ) \begin{equation} \begin{aligned} (\mu_0,\Sigma_0) = (H_k \hat{x}_k, H_k\hat{P}_kH_k^T) \end{aligned} \end{equation} (μ0,Σ0)=(Hkx^k,HkP^kHkT)
测量(measurement)满足:
( μ 1 , Σ 1 ) = ( z k ′ , R k ) \begin{equation} \begin{aligned} (\mu_1,\Sigma_1) = (z_k',R_k) \\ \end{aligned} \end{equation} (μ1,Σ1)=(zk′,Rk)
融合预测和测量:
K = H k P ^ k H k T ( R k + H k P ^ k H k T ) − 1 H k x k = H k x ^ k + K ( z k ′ − H k x ^ k ) H k P k H k T = H k P ^ k H k T − K H k P ^ k H k T \begin{equation} \begin{aligned} K &= H_k\hat{P}_kH_k^T(R_k + H_k\hat{P}_kH_k^T)^{-1} \\ H_kx_k &= H_k\hat{x}_k + K(z_k' - H_k\hat{x}_k) \\ H_kP_kH_k^T &= H_k\hat{P}_kH_k^T - KH_k\hat{P}_kH_k^T \\ \end{aligned} \end{equation} KHkxkHkPkHkT=HkP^kHkT(Rk+HkP^kHkT)−1=Hkx^k+K(zk′−Hkx^k)=HkP^kHkT−KHkP^kHkT
化简之后:
K = P ^ k H k T ( R k + H k P ^ k H k T ) − 1 x k = x ^ k + K ′ ( z k ′ − H k x ^ k ) P k = P ^ k − K ′ H k P ^ k \begin{equation} \begin{aligned} K &= \hat{P}_kH_k^T(R_k + H_k\hat{P}_kH_k^T)^{-1} \\ x_k &= \hat{x}_k + K'(z_k' - H_k\hat{x}_k) \\ P_k &= \hat{P}_k - K'H_k\hat{P}_k \\ \end{aligned} \end{equation} KxkPk=P^kHkT(Rk+HkP^kHkT)−1=x^k+K′(zk′−Hkx^k)=P^k−K′HkP^k
这里的 K K K 被称为卡尔曼增益。观察(8)中的 x x x变化,其中后半部分体现的是观测和预测的差,而卡尔曼增益即为该项的权重。
相关文章:

拓展卡尔曼滤波EKF
How to fusion two Gauss Distribution N ( x , μ 0 , σ 0 ) N ( x , μ 1 , σ 1 ) N ( x , μ ′ , σ ′ ) \begin{equation} \begin{aligned} \mathcal{N}(x,\mu_0,\sigma_0) \mathcal{N}(x,\mu_1,\sigma_1) \mathcal{N}(x,\mu,\sigma) \\ \end{aligned} \end{equatio…...
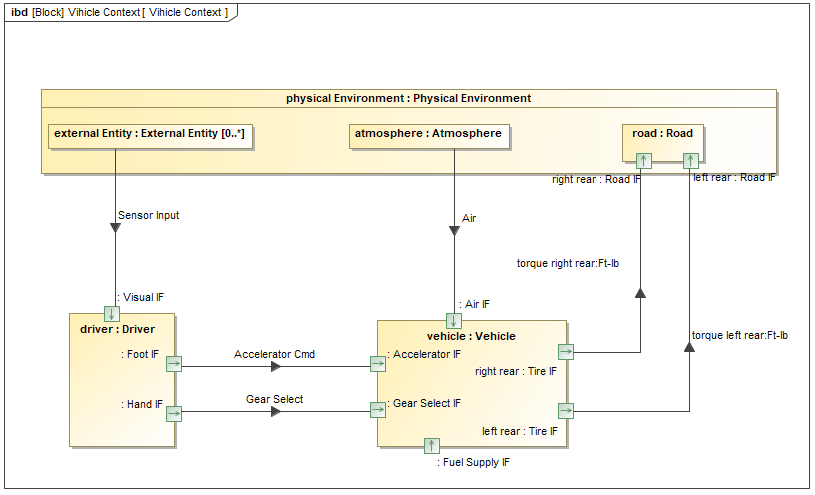
第四章 应用SysML基本特性集的汽车示例 P2(断更)|系统建模语言SysML实用指南学习
仅供个人学习 使用试用版CSM很鸡肋,然后书中一些内容没有说明,自定义方面有点困难,第四章暂时停止 同时感觉画图的顺序也很随意?甚至需求图放在了后面,觉得很离谱。 准备跳过这一章节 汽车模型 续P1 序列图表示启…...

Vue入门——核心知识点
简介 Vue是一套用于构建用户界面的渐进式JS框架。 构建用户界面:就是将后端返回来的数据以不同的形式(例如:列表、按钮等)显示在界面上。渐进式:就是可以按需加载各种库。简单的应用只需要一个核心库即可,复杂的应用可以按照需求…...
使用opencv的tracking模块跟踪目标
OpenCV跟踪模块算法介绍 OpenCV的tracking模块是一个功能强大的跟踪算法库,包含多种用于跟踪对象的算法。它可以帮助你在连续的视频帧中定位一个物体,例如人脸、眼睛、车辆等。 在OpenCV的tracking模块中,一些主要的跟踪算法包括࿱…...
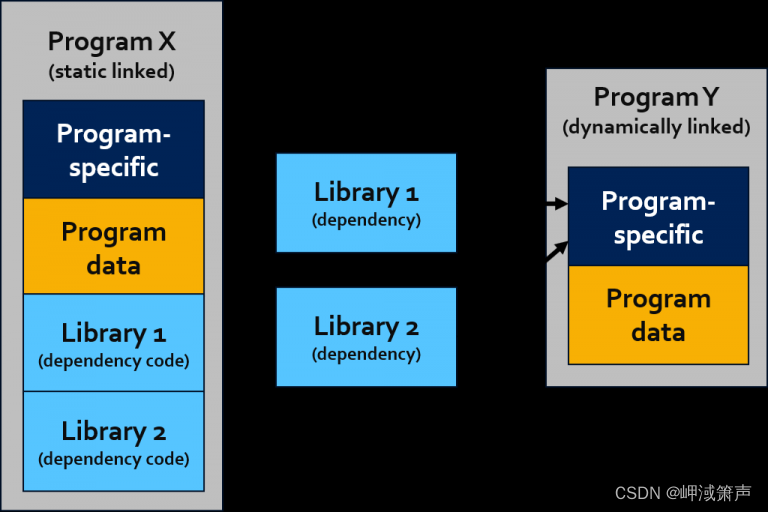
Debian或Ubuntu静态交叉编译arm和aarch64
Debian或Ubuntu静态交叉编译arm和aarch64 介绍术语ARM架构前置条件从源代码编译一个简单的C程序configure和make交叉编译关于静态链接和依赖关系使用 musl libc 实现与 configure 和 make 进行交叉编译 ARM 正在获得越来越多的关注,并且越来越受欢迎。直接在这些基于…...
最新ai系统ChatGPT程序源码+详细搭建教程+以图生图+Dall-E2绘画+支持GPT4+Midjourney绘画
一、AI创作系统 SparkAi创作系统是基于OpenAI很火的ChatGPT进行开发的Ai智能问答系统和Midjourney绘画系统,支持OpenAI-GPT全模型国内AI全模型。本期针对源码系统整体测试下来非常完美,可以说SparkAi是目前国内一款的ChatGPT对接OpenAI软件系统。那么如…...
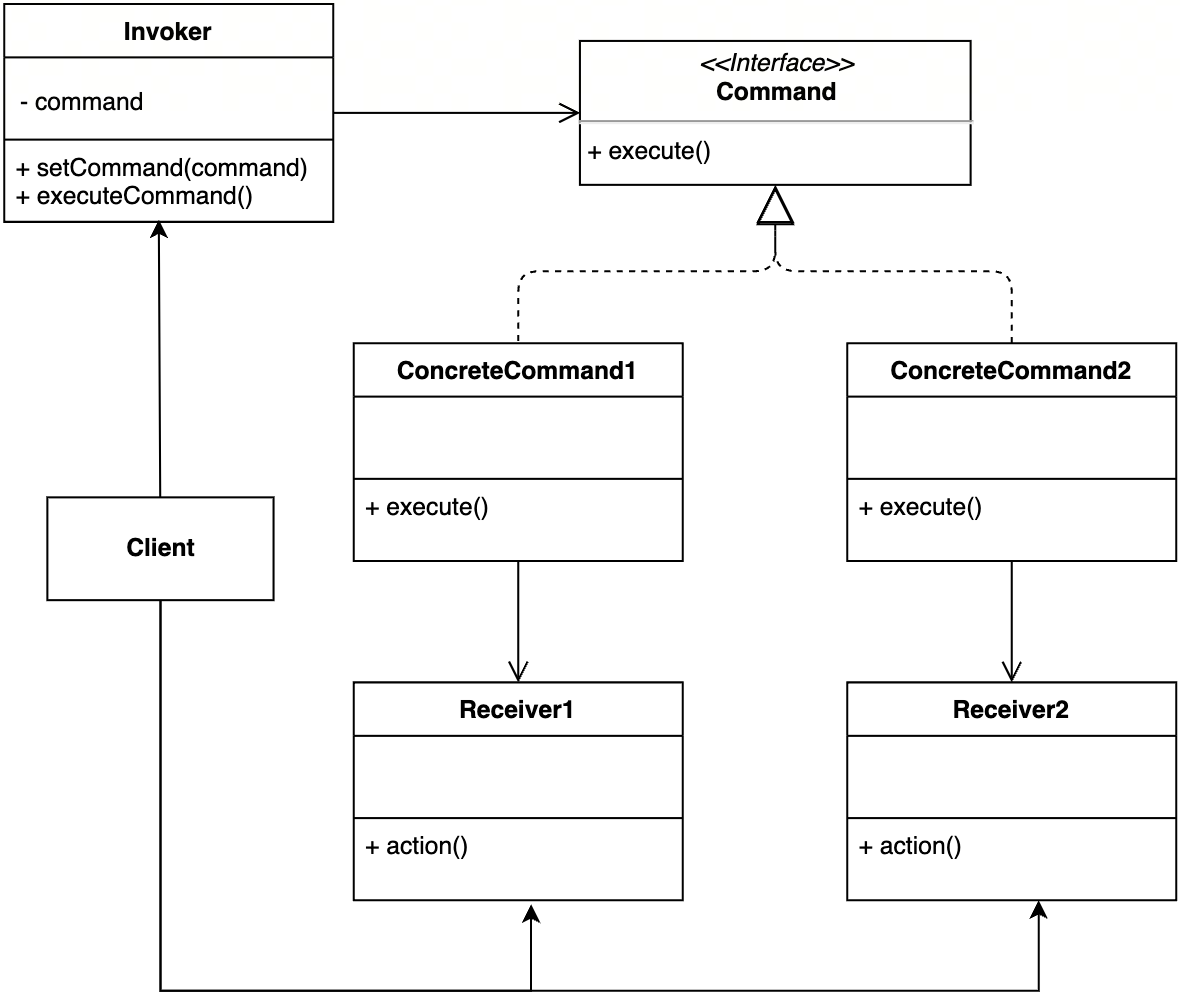
【设计模式】第16节:行为型模式之“命令模式”
一、简介 命令模式:将请求(命令)封装为一个对象,这样可以使用不同的请求参数化其他对象(将不同请求依赖注入到其他对象),并且能够支持请求(命令)的排队执行、记录日志、…...
安装pytorch报错torch.cuda.is_available()=false的解决方法
参考文章: https://blog.csdn.net/qq_46126258/article/details/112708781 https://blog.csdn.net/Andy_Luke/article/details/122503884 https://blog.csdn.net/anmin8888/article/details/127910084 https://blog.csdn.net/zcs2632008/article/details/127025294 …...
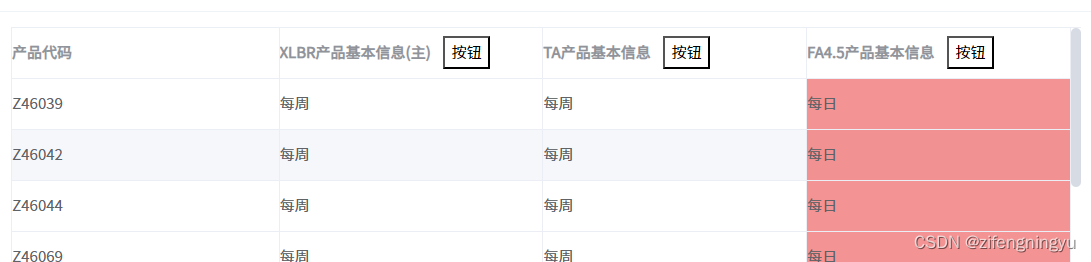
自定义表格的表头根据后端的数据进行筛选是否进行自定义表头添加按钮
自定义表格的表头根据后端的数据进行筛选是否进行自定义表头添加按钮 自定义表格的表头根据后端的数据进行筛选是否进行自定义表头添加按钮 <template><div class"box"><el-table :data"msgMapList" border class"table">&l…...

海上风电应急救援vr模拟安全培训提高企业风险防范能力
相比传统的发电厂,海上风电作业积累的经验少,风险高,因此为了规范施工人员的行为和操作,保障生产安全进行,开展海上风电VR安全培训具有重要意义。 有助于提高员工的安全意识 通过模拟真实的海上风电作业环境࿰…...
自定义SpringBoot启动图标
在SpringBoot项目的resources目录下创建banner.txt文件 在https://www.bootschool.net/网站上复制Ascll艺术字(图)粘贴到banner.txt中保存。 启动项目就会加载 可以修改颜色,和版本号 ${application.version} 输出版本 ${spring-boot.v…...
diffusers-Tasks
https://huggingface.co/docs/diffusers/using-diffusers/unconditional_image_generationhttps://huggingface.co/docs/diffusers/using-diffusers/unconditional_image_generation1.Unconditional image generation 无条件图像生成是一个相对简单的任务。模型仅生成图像&…...

文件下载漏洞, 漏洞原理, 测试方法, 漏洞防御, 常见敏感路径
文件下载漏洞 一, 文件下载漏洞原理 利用条件: 1. 读取文件的路径是用户可控, 且没有校验或检验不严. 2. 使用了读取文件的函数. 3. 输出了文件内容.漏洞场景一: 后端没有限制哪些路径的文件可以下载 后端代码: http://192.168.112.200/security/download.php $file_pat…...
【零参考GAN:Pansharpening】
ZeRGAN: Zero-Reference GAN for Fusion of Multispectral and Panchromatic Images (用于多光谱和全色图像融合的零参考GAN) 本文提出了一种融合低空间分辨率多光谱(LR MS)和高空间分辨率全色(PAN)图像的新的全色锐化方法–零参考生成对抗网络(ZeRGAN…...

Nacos 注册中心介绍与实操
前言 本文为个人SpringCloud学习笔记,主要记录Nacos的注册中心实操、SpringBoot多模块编程实操等 注册中心 注册中心介绍 注册中心是微服务的一个重要组件,用于实现服务的注册与发现,主要作用包括以下: 服务注册:…...
基于51单片机的智能手机充电器设计
**单片机设计介绍,1660【毕设课设】基于51单片机和MAX1898的智能手机充电器设计 文章目录 一 概要二、功能设计设计思路 三、 软件设计原理图 五、 程序六、 文章目录 一 概要 51单片机智能手机充电器设计介绍 51单片机智能手机充电器是一种可以实现智能快速充电的…...

nginx 和gateway配置实现动静分离和反向代理
这两个配置文件分别是Nginx和Spring Cloud Gateway的配置文件,它们用于构建网关服务,进行请求的路由和转发。 前端发送请求的时候为了不暴露服务器地址,所以会使用nginx做反向代理的一个主要作用是隐藏后端服务器的真实地址,从而增加网络安全…...
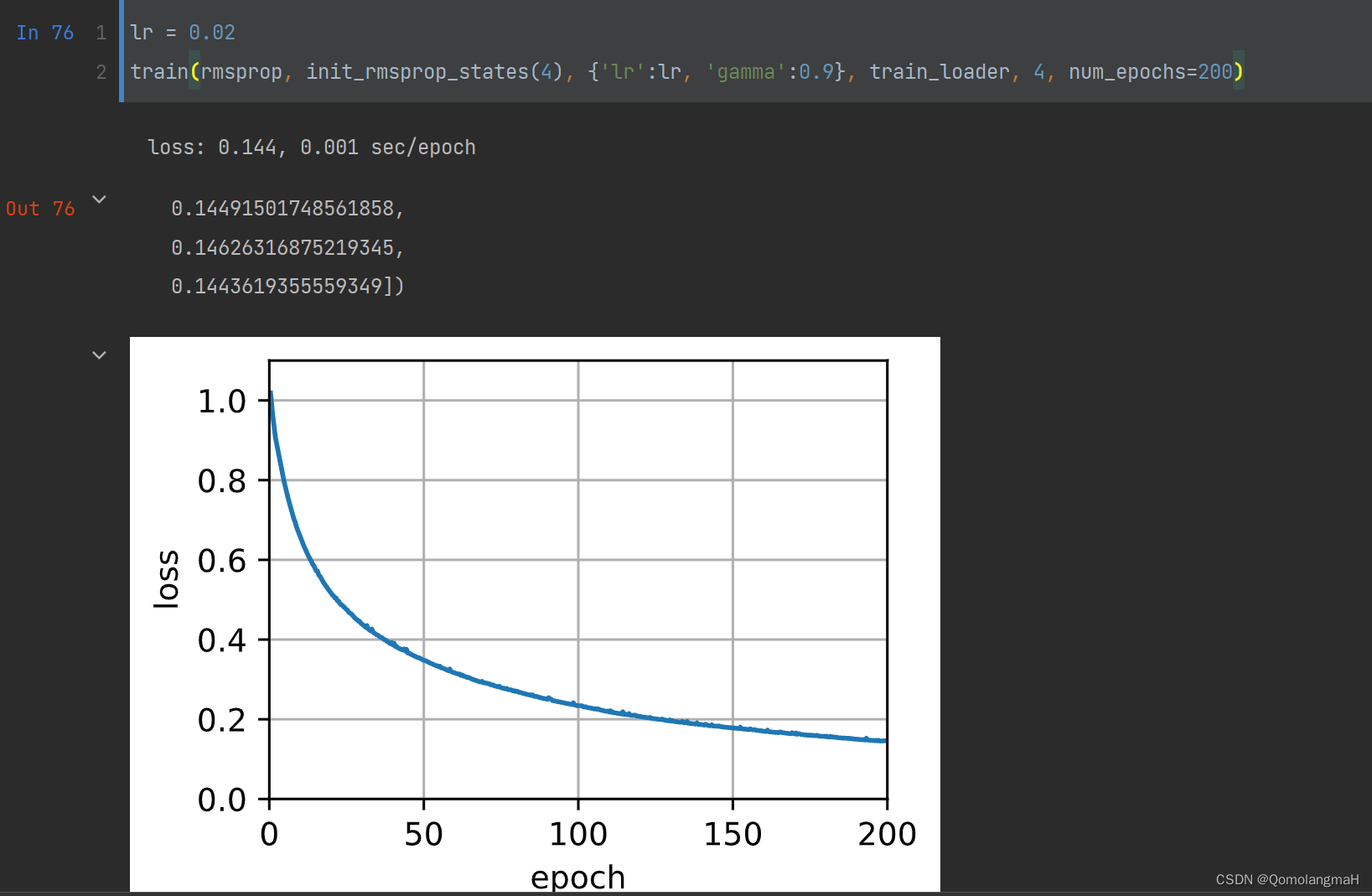
【深度学习实验】网络优化与正则化(二):基于自适应学习率的优化算法详解:Adagrad、Adadelta、RMSprop
文章目录 一、实验介绍二、实验环境1. 配置虚拟环境2. 库版本介绍 三、实验内容0. 导入必要的库1. 随机梯度下降SGD算法a. PyTorch中的SGD优化器b. 使用SGD优化器的前馈神经网络 2.随机梯度下降的改进方法a. 学习率调整b. 梯度估计修正 3. 梯度估计修正:动量法Momen…...

系统韧性研究(3)| 工程系统韧性要求
从最基本的层面上说,系统韧性指的是系统在逆境中继续执行其任务的程度。虽然对操作连续性至关重要,但系统的服务(能力)只是系统继续执行其任务所必须保护的一些资产。该系统必须检测不利因素,对其作出反应,…...
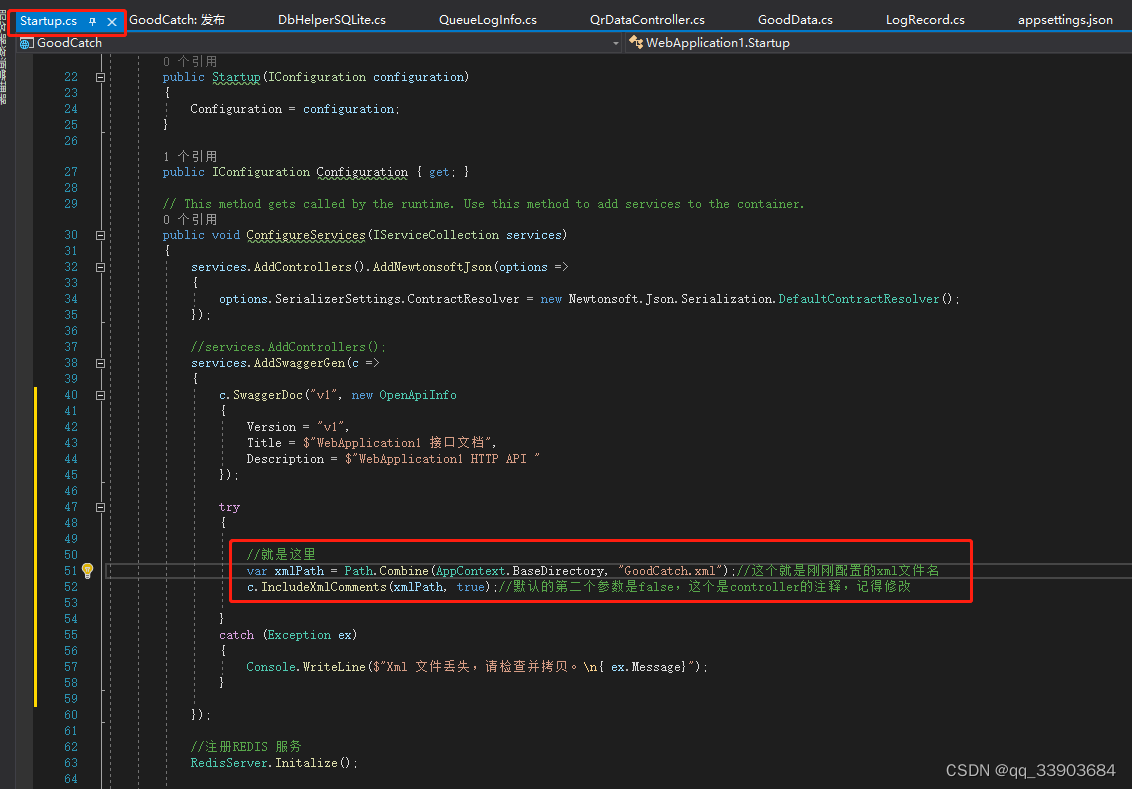
.net 5 发布后swagger页面不显示问题
1:项目右键属性-》生成xml--用于swagger文件读取 2:开启文件配饰swagger读取指定文件...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...

CppCon 2015 学习:Time Programming Fundamentals
Civil Time 公历时间 特点: 共 6 个字段: Year(年)Month(月)Day(日)Hour(小时)Minute(分钟)Second(秒) 表示…...

游戏开发中常见的战斗数值英文缩写对照表
游戏开发中常见的战斗数值英文缩写对照表 基础属性(Basic Attributes) 缩写英文全称中文释义常见使用场景HPHit Points / Health Points生命值角色生存状态MPMana Points / Magic Points魔法值技能释放资源SPStamina Points体力值动作消耗资源APAction…...

Java多线程实现之Runnable接口深度解析
Java多线程实现之Runnable接口深度解析 一、Runnable接口概述1.1 接口定义1.2 与Thread类的关系1.3 使用Runnable接口的优势 二、Runnable接口的基本实现方式2.1 传统方式实现Runnable接口2.2 使用匿名内部类实现Runnable接口2.3 使用Lambda表达式实现Runnable接口 三、Runnabl…...
)
使用python进行图像处理—图像滤波(5)
图像滤波是图像处理中最基本和最重要的操作之一。它的目的是在空间域上修改图像的像素值,以达到平滑(去噪)、锐化、边缘检测等效果。滤波通常通过卷积操作实现。 5.1卷积(Convolution)原理 卷积是滤波的核心。它是一种数学运算,…...
