UVA 11990 “Dynamic‘‘ Inversion 区域树 + 树状数组
一、题目大意
我们有 1 2 3 ... n 这些数字组成的一个排列数组 a ,需要从这个排列中取出m个数字,要求计算出出每次取出数字之前,数组中的逆序数(逆序数就是 i < j,但是 ai > aj的数)
二、解题思路
我们以数组为基础构建一颗区域树,每个节点保存下标在 [l , r)的元素,并按照元素的值排序。
针对于题目的开始,我们可以计算 0<=i<n 的所有ai,j < i 但 aj > ai的个数,这个数量求和即最初的逆序数,计算的方式就是去区域树上查到 [0 , i)区间内的节点,每个节点 lower_bound计数,求出sum。(因为每个元素都循环,所以仅考虑它前面的元素即可,后面的元素会在循环时计算到)
然后针对每次要移除的数字 ai,只需要去 [0 , i)区间的树节点依次进行二分即可知道 j < i,且 aj > ai的个数 x,然后去 [i+1 , n)的数节点进行二分,即可知道 j > i,且aj < ai的个数 y,sum=sum-x-y
每次移除数字之前,输出sum
同时数字被移除了,下次要避免重复计算,所以可以对区域上每个节点建立一个树状数组,每次移除一个数字时,需要去当前数字的节点和它的父节点上,用过二分找到这个数组的下标,将下标+1的位置更新1(树状数组的有效下标从1开始),注意也要循环更新父节点 ( p = (p - 1)/2)
这样每次去区域树上lower_bound得到idx时,通过树状数组求和两次([1,idx],[1,l-r]),去掉那些已经被移除的数字,即可避免重复计算。
三、代码
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long ll;
int *bit[524288];
int *dat[524288];
int datL[524288], datR[524288];
int n, m, num[200007], seq[200007], num2Idx[200007];
int _current, _currentLt, _currentGt;
char opType;
void input()
{for (int i = 0; i < n; i++){scanf("%d", &num[i]);num2Idx[num[i]] = i;}for (int i = 0; i < m; i++){scanf("%d", &seq[i]);}
}
int calcSize(int _size)
{int size = 1;while (size < _size){size = size * 2;}return size;
}
void build(int i, int l, int r)
{if (r - l == 1){dat[i] = new int[1];dat[i][0] = num[l];}else{int lch = i * 2 + 1;int rch = i * 2 + 2;int mid = (l + r) / 2;build(lch, l, mid);build(rch, mid, r);dat[i] = new int[r - l];merge(dat[lch], dat[lch] + (mid - l), dat[rch], dat[rch] + (r - mid), dat[i]);}datL[i] = l;datR[i] = r;int size = calcSize(r - l);bit[i] = new int[size + 1];for (int j = 0; j <= size; j++){bit[i][j] = 0;}
}
int sum(int idx, int i)
{int res = 0;for (int j = i; j > 0; j = j - (j & (-j))){res = res + bit[idx][j];}return res;
}
void update(int idx, int i, int x, int size)
{if (i <= 0){return;}for (int j = i; j <= size; j = j + (j & (-j))){bit[idx][j] = bit[idx][j] + x;}
}
void queryCnt(int i, int l, int r)
{int lt = lower_bound(dat[i], dat[i] + (r - l), _current) - dat[i];int size = calcSize(r - l);int realLt = lt - sum(i, lt);int realAll = (r - l) - sum(i, size);int realGt = realAll - realLt;_currentLt = _currentLt + realLt;_currentGt = _currentGt + realGt;
}
void updateTree(int i)
{update(i, 1, 1, 1);int j = i;while (j > 0){j = (j - 1) / 2;int idx = lower_bound(dat[j], dat[j] + (datR[j] - datL[j]), _current) - dat[j];int size = calcSize(datR[j] - datL[j]);update(j, idx + 1, 1, size);}
}
void query(int _l, int _r, int i, int l, int r, char opType)
{if (_l >= r || _r <= l){}else if (l >= _l && r <= _r){if (opType == 'q'){queryCnt(i, l, r);}if (opType == 'u'){updateTree(i);}}else{query(_l, _r, i * 2 + 1, l, (l + r) / 2, opType);query(_l, _r, i * 2 + 2, (l + r) / 2, r, opType);}
}
void solve()
{ll val = 0LL;for (int i = 0; i < n; i++){_current = num[i];_currentLt = 0, _currentGt = 0;query(0, i, 0, 0, n, 'q');val = val + _currentGt;}for (int i = 0; i < m; i++){printf("%lld\n", val);_current = seq[i];_currentLt = 0, _currentGt = 0;query(0, num2Idx[seq[i]], 0, 0, n, 'q');val = val - _currentGt;_currentLt = 0, _currentGt = 0;query(num2Idx[seq[i]] + 1, n, 0, 0, n, 'q');val = val - _currentLt;query(num2Idx[seq[i]], num2Idx[seq[i]] + 1, 0, 0, n, 'u');}
}
int main()
{while (~scanf("%d%d", &n, &m)){input();build(0, 0, n);solve();}return 0;
}相关文章:

UVA 11990 “Dynamic‘‘ Inversion 区域树 + 树状数组
一、题目大意 我们有 1 2 3 ... n 这些数字组成的一个排列数组 a ,需要从这个排列中取出m个数字,要求计算出出每次取出数字之前,数组中的逆序数(逆序数就是 i < j,但是 ai > aj的数) 二、解题思路 …...
邮件钓鱼分析
三大协议 SPF Sender Policy Framework 的缩写,一种以IP地址认证电子邮件发件人身份的技术。 注:收信人怀疑币是假的,查看这个送信包裹里面记录的发出地是不是央行,如果是黑市有可能是黑钱 DKIM 加密签名和域名关联。 注&am…...

Android 小技巧
1. Android Studio下载地址 Android 开发者 | Android Developers (google.cn) 2.Android Aosp 在线查看地址: AOSPXRef 3.Android 官方文档地址: Android 开源项目 | Android Open Source Project (google.cn)...

Centos MySQL --skip-grant-tables详解
跳过权限验证,导出数据备份 主机系统:Centos7 64位 数据库版本:MySQL5.7.40 使用–skip-grant-tables场景 1、忘记管理员密码 2、修改管理员密码 mysql -uroot -p显示错误内容如下: ERROR 1045 (28000): Access denied for …...
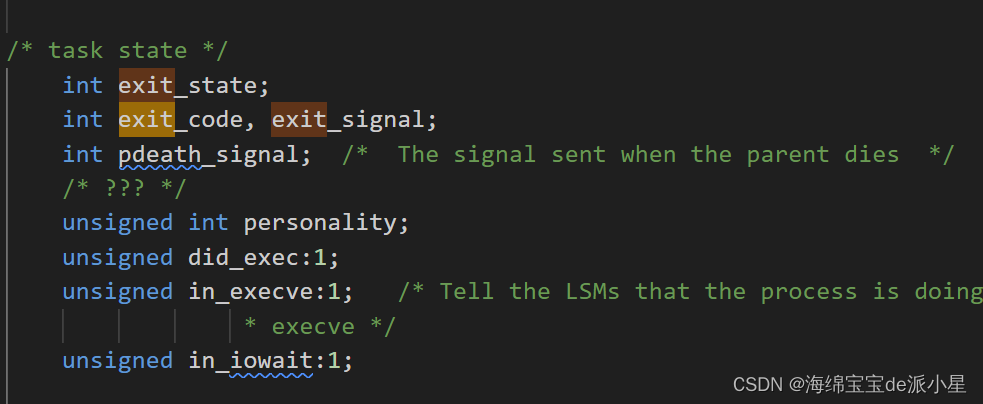
Linux:进程控制的概念和理解
文章目录 进程的创建fork函数写时拷贝的原理fork函数的用法和失败原因 进程终止进程的退出进程异常的问题 进程终止进程退出 进程等待什么是进程等待?为什么要进行进程等待?如何进行进程等待?父进程如何知道子进程的退出信息? wai…...

ubuntu20.04编译安装nginx
目录 一.更新系统软件包列表二.安装编译Nginx所需的依赖三.下载Nginx源代码四.解压源代码文件五.进入解压后的Nginx目录六.配置编译选项七.编译并安装Nginx八.启动Nginx服务九.验证Nginx是否正常运行十.Nginx命令十一.配置软链接 在Ubuntu 20.04上编译安装Nginx,你可…...

操作系统的分页
操作系统的分页功能与内存管理密切相关。为了更好地理解这一点,我们先简要概述分页的基本概念,然后解释其与页面调度和存储效率的关系。 分页的基本概念 分页是操作系统中的一种内存管理策略。物理内存被划分为固定大小的块,称为“页面”或“…...

微服务环境搭建
JDK安装:https://blog.csdn.net/JHYPXS/article/details/134155680 mysql安装:https://blog.csdn.net/JHYPXS/article/details/102566304 nacos安装:https://nacos.io/zh-cn/docs/v2/quickstart/quick-start.html...
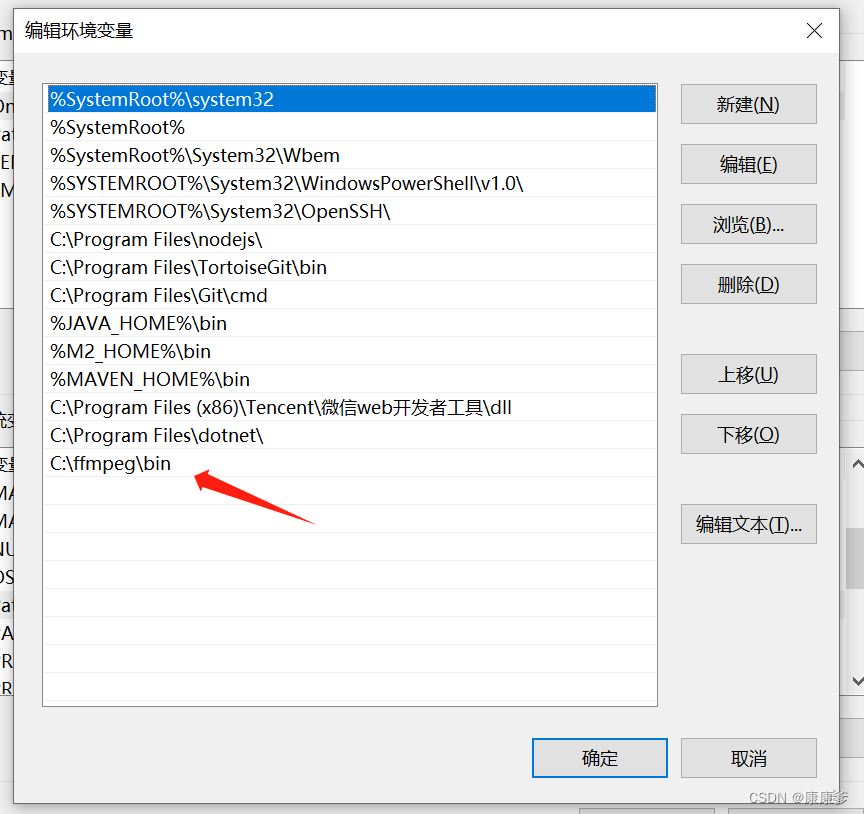
ffmpeg 截取命令
从00:00:03.500开始截取往后长度到结尾的mp3音频(这个更有用,测试好用) ffmpeg -i d:/c.mp3 -ss 00:00:03.500 d:/output.mp3 将两个音频合并成一个音频(测试好用) ffmpeg -i "concat:d:/c.mp3|d:/output.mp3&…...

TypeScript深度剖析:TypeScript 中枚举类型应用场景?
文章目录 一、是什么二、使用数字枚举字符串枚举异构枚举本质 三、应用场景 一、是什么 枚举是一个被命名的整型常数的集合,用于声明一组命名的常数,当一个变量有几种可能的取值时,可以将它定义为枚举类型 通俗来说,枚举就是一个对象的所有可能取值的集…...
[推荐]SpringBoot,邮件发送附件含Excel文件(含源码)。
在阅读本文前,可以先阅读我的上一篇文章: SpringBoot,使用JavaMailSender发送邮件(含源码)。 ,本文使用的代码案例涉及到的 jar包、application.properties配置与它相同。 先看一下效果。 图一 图二 在下方代码案例中,…...

node学习之包管理器
一、概念介绍 **1.1 包是什么 ** 『包』英文单词是 package ,代表了一组特定功能的源码集合 **1.2 包管理工具 ** 管理『包』的应用软件,可以对「包」进行 下载安装 , 更新 , 删除 , 上传 等操作 借助包管理工具&…...

自动驾驶车辆轨迹跟踪
相对于传统的模型预测控制(MPC),简化的车辆模型通常会导致预测结果不准确,这对车辆的转弯等行为具有负面影响。因此作者提出了一种轨迹规划和跟踪框架: 该框架应用人工势场来获得目标轨迹;并利用具有PID反…...

React的useEvent 和 ahooks 的 useMemorizedFn 的深度分析和对比
父组件 const TestParent: React.FC<any> () > {const [State, setState] useState(0);const changeFun useCallback(() > {console.log(useCallback closure 里的 State, State);}, [State]);const changeFun_useEvent useEvent(() > {console.log(useEv…...
基于goframe2.5.4、vue3、tdesign-vue-next开发的全栈前后端分离的管理系统
goframe-admin goframe-admin V1.0.0 平台简介 基于goframe2.5.4、vue3、tdesign-vue-next开发的全栈前后端分离的管理系统。前端采用tdesign-vue-next-starter 、vue3、pinia、tdesign-vue-next。 特征 高生产率:几分钟即可搭建一个后台管理系统认证机制&#x…...

LInux之在同一Tomcat下使用不同的端口号访问不同的项目
🎉🎉欢迎来到我的CSDN主页!🎉🎉 🏅我是君易--鑨,一个在CSDN分享笔记的博主。📚📚 🌟推荐给大家我的博客专栏《LInux实战开发》。🎯🎯 …...

梦百合上榜2023鼎革奖数字化转型先锋榜
10月26日,第六届“鼎革奖”数字化转型先锋榜单揭晓,梦百合家居凭借数字化生产的卓越成果——SAP管理平台及供应链项目,入选2023【鼎革奖】数字化转型先锋榜年度供应链转型典范,梦百合家居COO 崔慧明同步入选2023【鼎革奖】数字化转型先锋榜年度首席运营官。 据了解,「鼎革奖」数…...

沉痛悼念科研分公司
今天上班途中,遇到了上家公司的同事王强。他正准备去体检中心体检。几句寒暄之后,得知他是要入职选煤公司了。 我们所在的公司比较大,总公司下设有几十个分、子公司,我和他曾经在一家子公司——科研分公司。现在的科研分公司解散…...
+Nginx】)
Django的网站项目开发好了,该用何种方案在Centos上部署【答:Gunicorn(uWSGI)+Nginx】
问:用Django开发的网站开发好了,现在要部署上线。 系统为Centos 7.x 现在我安装好Django和相关依赖后,我用命令 python manage.py runserver 127.0.0.1:8010 启动Django 然后安装配置好Nginx,并把用的请求转发到 127.0.0.1:8010 。 请问这样的…...
基于PyTorch的中文情绪分析器设计与开发
收藏和点赞,您的关注是我创作的动力 文章目录 概要 一、相关基础理论2.1 主流深度学习框架2.2 神经网络2.2.1 神经网络基础 二、中文情感分类模型构建3.1 开发环境3.2 数据部分3.3 文本特征提取3.3.1、过滤标点符号3.3.2 中文分词、单词过滤 三 运行结果与分析五 结…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...
零知开源——STM32F103RBT6驱动 ICM20948 九轴传感器及 vofa + 上位机可视化教程
STM32F1 本教程使用零知标准板(STM32F103RBT6)通过I2C驱动ICM20948九轴传感器,实现姿态解算,并通过串口将数据实时发送至VOFA上位机进行3D可视化。代码基于开源库修改优化,适合嵌入式及物联网开发者。在基础驱动上新增…...

Java求职者面试指南:Spring、Spring Boot、Spring MVC与MyBatis技术解析
Java求职者面试指南:Spring、Spring Boot、Spring MVC与MyBatis技术解析 一、第一轮基础概念问题 1. Spring框架的核心容器是什么?它的作用是什么? Spring框架的核心容器是IoC(控制反转)容器。它的主要作用是管理对…...

UE5 音效系统
一.音效管理 音乐一般都是WAV,创建一个背景音乐类SoudClass,一个音效类SoundClass。所有的音乐都分为这两个类。再创建一个总音乐类,将上述两个作为它的子类。 接着我们创建一个音乐混合类SoundMix,将上述三个类翻入其中,通过它管理每个音乐…...

游戏开发中常见的战斗数值英文缩写对照表
游戏开发中常见的战斗数值英文缩写对照表 基础属性(Basic Attributes) 缩写英文全称中文释义常见使用场景HPHit Points / Health Points生命值角色生存状态MPMana Points / Magic Points魔法值技能释放资源SPStamina Points体力值动作消耗资源APAction…...
)
MySQL基本操作(续)
第3章:MySQL基本操作(续) 3.3 表操作 表是关系型数据库中存储数据的基本结构,由行和列组成。在MySQL中,表操作包括创建表、查看表结构、修改表和删除表等。本节将详细介绍这些操作。 3.3.1 创建表 在MySQL中&#…...

qt 双缓冲案例对比
双缓冲 1.双缓冲原理 单缓冲:在paintEvent中直接绘制到屏幕,绘制过程被用户看到 双缓冲:先在redrawBuffer绘制到缓冲区,然后一次性显示完整结果 代码结构 单缓冲:所有绘制逻辑在paintEvent中 双缓冲:绘制…...
MySQL 数据库深度剖析:事务、SQL 优化、索引与 Buffer Pool
在当今数据驱动的时代,数据库作为数据存储与管理的核心,其性能与可靠性至关重要。MySQL 作为一款广泛使用的开源数据库,在众多应用场景中发挥着关键作用。在这篇博客中,我将围绕 MySQL 数据库的核心知识展开,涵盖事务及…...
