动态规划实例——换零钱的方法数(C++详解版)
原写了 Java 版本的如何求解换钱的方法数,近期进行了一些细节上的补充,以及部分错误更正,将语言换为了 C++ 语言。
基础题目
假设你现在拥有不限量的 1 元、5 元、10 元面值纸币,路人甲希望找你换一些零钱,路人甲拿出的是一张 100 元面值的纸币,试求总共有多少种换零钱的方法?
分析:因为总共只有 3 种面值小额纸币,所以将所有可能进行枚举,直接暴力解决即可。
#include<bits/stdc++.h>
using namespace std;int slove() {int ans = 0;// 10 元张数for(int i = 0; i <= 10; i++) {// 5 元张数for(int j = 0; j <= 20; j++) {// 1 元张数for(int k = 0; k <= 100; k++) {int cur = i*10 + j*5 + k*1;if(cur == 100) {ans++;}}}}return ans;
}int main()
{cout<<slove();
}
递归求解
基础题目中是拥有固定种类的小额纸币,即使再多几种小额纸币也没关系,大不了在嵌套几个循环就能解决。现在需要将题目的难度加大一点,改为小额纸币的种类和需要换零钱的总额由用户输入,即小额纸币种类和总额都不在固定,那么如何解决?
输入共有三行:
- 第一行:小额纸币种类数量
- 第二行:不同小额纸币的面值
- 第三行:需要换零钱的总额
分析:虽然现在种类和总额都是变量了,但是上文中的基础版本还是被包含在此问题中,所以我们还是以上文中的 1 元、5 元、10 元换 100 元进行分析,找一找除了枚举是否还有其他方法解决。
我们先固定一种零钱的数量,剩下的钱用剩余零钱去兑换,即:
- 用 0 张 1 元换,剩下的用 5、10 元换,最终方法数为 count0;
- 用 1 张 1 元换,剩下的用 5、10 元换,最终方法数为 count1;
- …
- 用 100 张 1 元换,剩下的用 5、10 元换,最终方法数为 count100;
那么最终换钱的方法综述即为count0 + count1 + count2 + ... + count100。
上面的分析中,我们把原来的大问题拆为了 101 个小问题,且每一个小问题都有很相似的地方,即:
- 求用 5、10 元换 100 元的方法数
- 求用 5、10 元换 95 元的方法数
- …
- 求用 5、10 元换 0 元的方法数
如果我们对这 101 个小问题再进行同样思路的分析,即再固定 5 元零钱的数量,那么就能把问题划分成了规模更小,但问题类型一样的小小问题。即递归的思路,可以写出如下代码。
#include<bits/stdc++.h>
using namespace std;// money 表示所有小额纸币的面值
// len 表示 money 数组的长度,即:小额纸币种类
// index 表示上文分析中的当前固定第几张
// target 表示现在要兑换的钱的总额
int slove(int money[], int len, int index, int target) {int ans = 0;if(index == len) {ans = target == 0 ? 1 : 0;} else {for(int i = 0; i*money[index] <= target; i++) {// 剩余待换零钱的总额int cur_total = target-(i * money[index]);ans = ans + slove(money, len, index+1, cur_total);}}return ans;
}int main()
{int m, target;int money[1000]; // 零钱具体面值cin>>m; // 零钱种类for(int i = 0; i < m; i++){cin>>money[i];}cin>>target; // 兑换总额cout<<slove(money, m, 0, target);
}
优化递归
可以发现上文所写的递归代码存在大量的重复过程,比如下面两种情况,后面所求的子问题是完全一样的,导致程序运行时间的浪费。
- 已经使用了 5 张 1 元、0 张 5 元,剩下的 95 元用 5 元和 10 元兑换
- 已经使用了 0 张 1 元、1 张 5 元,剩下的 95 元用 5 元 和 10 元兑换
既然前面已经求解过相同的子问题了,那么我们是否可以在第一次求解的时候,将计算结果保存下来,这样下次遇到相同子问题的实际,直接查出来用就可以,省去再次求解的时间。
#include<bits/stdc++.h>
using namespace std;// 用于存储子问题的解
int val_map[1000][1000] = { 0 };// 0 表示该子问题没有算过
// -1 表示算过,但该子问题无解
// 其它值,即此子问题的方法数int slove(int money[], int len, int index, int target) {int ans = 0;if(index == len) {ans = target == 0 ? 1 : 0;} else {for(int i = 0; i*money[index] <= target; i++) {// 剩余待换零钱的总额int cur_total = target-(i * money[index]);int pre_val = val_map[index+1][cur_total];// 如果 val 为 0,说明该子问题没有被计算过if(pre_val == 0) {ans = ans + slove(money, len, index+1, cur_total);} else {ans += pre_val == -1 ? 0 : pre_val;}}}// 存储计算结果val_map[index][target] = ans == 0 ? -1 : ans;return ans;
}int main()
{int m, target; // 零钱种类int money[1000]; // 零钱具体面值cin>>m;for(int i = 0; i < m; i++){cin>>money[i];}cin>>target;cout<<slove(money, m, 0, target);
}
动态规划
上面对递归的优化方案已经能看出来动态规划的影子了,沿着前文先计算再查表的思路继续思考,我们能否提前把所有子问题都计算出答案,对每个子问题都进行查表解决。也即将最初的递归方案改为循环的实现。
所有的递归都能改为循环实现
#include<bits/stdc++.h>
using namespace std;// 用于存储子问题的解
// val_map[i][j] 表示用 money[0...i] 的小面额零钱组成 j 元的方法数
int val_map[1000][1000] = { 0 };int slove(int money[], int len, int target) {// 第一列表示组成 0 元的方法数,所以为 1for (int i = 0; i < len; i++) {val_map[i][0] = 1;}// 第一行表示只使用 money[0] 一种钱币兑换钱数为i的方法数// 所以是 money[0] 的倍数的位置为 1,否则为 0for (int i = 1; money[0]*i <= target; i++) {val_map[0][money[0]*i] = 1;}for (int i = 1; i < len; i++) {for (int j = 1; j <= target; j++) {for (int k = 0; j >= money[i]*k; k++) {/* val_map[i][j] 的值为:用 money[0...i-1] 的零钱组成 j 减去 money[i] 的倍数的方法数因为相比 val_map[i-1][j],只是多了一种零钱的可选项*/val_map[i][j] += val_map[i-1][j-money[i]*k];}}}return val_map[len-1][target];
}int main()
{int m, target; // 零钱种类int money[1000]; // 零钱具体面值cin>>m;for(int i = 0; i < m; i++){cin>>money[i];}cin>>target;cout<<slove(money, m, target);
}
动归优化
在上文第一版动态规划代码的优化中已经能发现,其实val_map[i][j]的值由两部分组成,分别为:
- 用 money[0…i-1] 的零钱组成换 j 元的方法数
- 用 money[0…i-1] 的零钱换 j-money[i]*k(k=1,1,2,3…)元的方法数之和
对于第二种情况来说,其累加值实际上就是val_map[i][j-money[i]],即用money[0...i]的零钱换 j-money[i]元的方法数。至于具体为什么累加值与val_map[i][j-money[i]]相等,我们可以借助递归方法时的分析方式进行理解。
用 money[0…i-1] 的零钱组成换 j 元的方法数对应:
- 用 0 张 money[i] 换,剩下的用 money[0…i-1] 换
用 money[0…i-1] 的零钱换 j-money[i]*k(k=1,1,2,3…)元的方法数之和对应:
- 用 1 张 money[i] 换,剩下的用 money[0…i-1] 换
- 用 2 张 money[i] 换,剩下的用 money[0…i-1] 换
- …
所以第二部分的值即为val_map[i][j-money[i]]。依据此处的分析,我们可以在原有基础上去掉第三层循环,减少程序运行所花费的时间。
#include<bits/stdc++.h>
using namespace std;int val_map[1000][1000] = { 0 };int slove(int money[], int len, int target) {for (int i = 0; i < len; i++) {val_map[i][0] = 1;}for (int i = 1; money[0]*i <= target; i++) {val_map[0][money[0]*i] = 1;}for (int i = 1; i < len; i++) {for (int j = 1; j <= target; j++) {val_map[i][j] = val_map[i-1][j];// 此处需要比较 j 的大小,防止数组越界// 注意条件时 >= ,否则少计算 j 刚好为 money[i] 的情况if(j >= money[i]) {val_map[i][j] += val_map[i][j-money[i]];}}}return val_map[len-1][target];
}int main()
{int m, target; // 零钱种类int money[1000]; // 零钱具体面值cin>>m;for(int i = 0; i < m; i++){cin>>money[i];}cin>>target;cout<<slove(money, m, target);
}
空间压缩
仔细观察能发现,每一次更新val_map[i][j]的值时,它只依赖于上一行和当前这一行前面的元素。对于我们所求解的问题来说,它仅要求我们给出最终的答案即可,那么前面存储中间结果的那些元素实际上就会空间的浪费,因此我们可以思考一下如何在空间上进行压缩。
实际上我们只需要定义一个一维的数组,采用一些技巧对该数组进行滚动更新,按照合适的方向去更新数组,同样可以达到上面使用二维数组的效果。
#include<bits/stdc++.h>
using namespace std;int val_map[1000] = { 0 };int slove(int money[], int len, int target) {// 第一行,只用 money[0] 换零钱// 所以只能换 money[0] 倍数的钱for (int i = 0; money[0]*i <= target; i++) {val_map[money[0] * i] = 1;}for (int i = 1; i < len; i++) {for (int j = 1; j <= target; j++) {if(j >= money[i]) {// 在进行下面一步前 val_map[j] 的值就已经是 val_map[i-1][j] 了val_map[j] += val_map[j-money[i]];}}}return val_map[target];
}int main()
{int m, target; // 零钱种类int money[1000]; // 零钱具体面值cin>>m;for(int i = 0; i < m; i++){cin>>money[i];}cin>>target;cout<<slove(money, m, target);
}
相关文章:
)
动态规划实例——换零钱的方法数(C++详解版)
原写了 Java 版本的如何求解换钱的方法数,近期进行了一些细节上的补充,以及部分错误更正,将语言换为了 C 语言。 基础题目 假设你现在拥有不限量的 1 元、5 元、10 元面值纸币,路人甲希望找你换一些零钱,路人甲拿出的…...

linux c
射频驱动 管理硬件设备、分配系统资源 内核由中断服务程序 调度程序 内存管理程序 网络和进程间进程通信程序 linux支持动态加载内核模块 支持多处理smp机制 内核可以抢占preemptive linux系统拥有多个发行版,可能由一个组织 公司和个人发行 VGA兼容或者更…...

第十三章 系统错误消息 - 一般系统错误消息 S - Z
文章目录第十三章 系统错误消息 - 一般系统错误消息 S - Z第十三章 系统错误消息 - 一般系统错误消息 S - Z 错误代码描述<SUBSCRIPT>下标值不合法或Global引用过长。<SWIZZLE FAIL>打开了一个oref,然后试图在另一个无法引用的相关对象中进行搅拌。这可…...

移动web基础
初始缩小:布局视口大于视觉视口 初始放大:布局视口小于视觉视口 布局视口等于视觉视口(这种动作行为叫做理想视口) <meta name"viewport" content"width375" /> <meta name"viewport"…...

MyBatis和MyBatis_Plus有什么区别【面试常考题】
MyBatis和MyBatis_Plus的区别 MyBatis_Plus MyBatis_Plus 是一个 MyBatis 的增强工具,只是在 MyBatis 的基础上增强了却没有做改变,MyBatis-Plus支持所有MyBatis原生的特性,所有引入MyBatis-Plus不会对现有的MyBatis框架产生任何影响。 MyBa…...

华为OD机试用Python实现 -【统一限载货物数最小值】(2023-Q1 新题)
华为OD机试题 华为OD机试300题大纲统一限载货物数最小值题目描述输入描述输出描述说明示例一输入输出说明示例二输入输出说明Python 代码实现算法逻辑华为OD机试300题大纲 参加华为od机试,一定要注意不要完全背诵代码,需要理解之后模仿写出,通过率才会高。 华为 OD 清单查…...

Vue入门小练习
文章目录Hello VueVue文本指令Vue属性绑定Vue双向绑定Vue事件绑定Vue猜数字Vue简单计算器Vue简单计算器升级版Vue循环遍历Vue员工列表练习Vue小练习Vue显示隐藏相关使用一些简单的小案例来熟悉Vue的基本使用方法 Hello Vue <!DOCTYPE html> <html lang"en"…...

Oracle-09-集合运算符篇
2022年4月13日23:01:25 通过本章学习,您将可以:1、描述 SET 操作符2、将多个查询用 SET 操作符连接组成一个新的查询目录 🏆一、SET OPERATORS ⭐️1.1、UNION /UNION ALL ⭐️1.2、INSTERSECT ⭐️1.3、MINUS dz...
请求中特定的Cookie)
获取浏览器(服务端)请求中特定的Cookie
有必要解释一下HttpServletRequest接口,因为我们需要从它里面获取Cookie。 HttpServletRequest HttpServletRequest是一个Java接口,提供了访问HTTP请求信息的方法,例如HTTP方法、请求URI、头部、参数和会话属性。它是Java Servlet API的一部…...
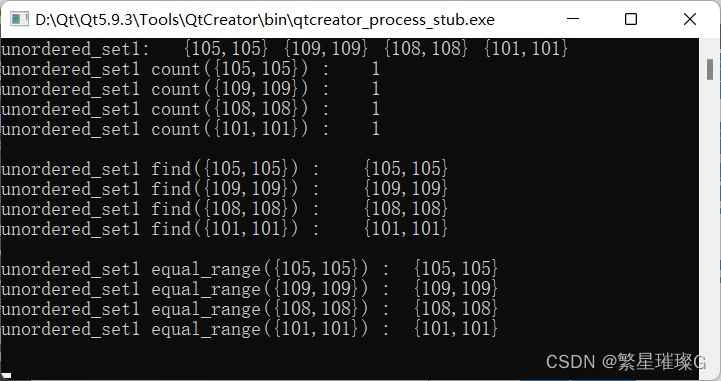
c++11 标准模板(STL)(std::unordered_set)(九)
定义于头文件 <unordered_set>template< class Key, class Hash std::hash<Key>, class KeyEqual std::equal_to<Key>, class Allocator std::allocator<Key> > class unordered_set;(1)(C11 起)namespace pmr { templat…...
)
python实战应用讲解-【实战应用篇】文件操作(附python示例代码)
目录 知识储备 使用 python-libarchive-c 模块 创建压缩文件 解压文件 查看信息...

OpenCV-Python系列(二)—— 图像处理(灰度图、二值化、边缘检测、高斯模糊、轮廓检测)
一、【灰度图、二值化】 import cv2 img cv2.imread("lz2.png") gray_img cv2.cvtColor(img, cv2.COLOR_BGR2GRAY) # 灰度图 # 二值化,(127,255)为阈值 retval,bit_img cv2.threshold(gray_img, 127, 255, cv2.THRESH_BINARY) cv2.imshow(photo1,im…...
ccc-台大林轩田机器学习基石-hw1
文章目录Question1-14Question15-PLAQuestion16-PLA平均迭代次数Question17-不同迭代系数的PLAQuestion18-Pocket_PLAQuestion19-PLA的错误率Question20-修改Pocket_PLA迭代次数Question1-14 对于有明确公式和定义的不需要使用到ml 智能系统在与环境的连续互动中学习最优行为策…...

hadoop03-MapReduce【尚硅谷】
大数据学习笔记 MapReduce 一、MapReduce概述 MapReduce是一个分布式运算程序的编程框架,是基于Hadoop的数据分析计算的核心框架。 MapReduce处理过程为两个阶段:Map和Reduce。 Map负责把一个任务分解成多个任务;Reduce负责把分解后多任务处…...

测牛学堂:软件测试python学习之异常处理
python的捕获异常 程序在运行时,如果python解释器遇到一个错误,则会停止程序的执行,并且提示一些错误信息,这就是异常。 程序停止执行并且提示错误信息,称之为抛出异常。 因为程序遇到错误会停止执行,有时…...

图神经网络--图神经网络
图神经网络 图神经网络图神经网络一、PageRank简介1.1互联网的图表示1.2PageRank算法概述1.3求解PageRank二、代码实战2.1引入库2.2加载数据,并构建图2.3计算每个节点PageRank重要度2.4用节点尺寸可视化PageRank值一、PageRank简介 PageRank是Google最早的搜索引擎…...

React useCallback如何使其性能最大化?
前言 React中最让人畅谈的就是其带来的灵活性,可以说写起来非常的舒服。但是也就是它的灵活性太强,往往让我们忽略了很多细节的地方,而就是这些细节的东西能进行优化,减小我们的性能开销。可以说刚学React和工作几年后写React的代…...
长尾关键词使用方法,通过什么方式挖掘长尾关键词?
当你在搜索引擎的搜索栏中输入有关如何使用长尾关键词的查询时,你可能希望有简单快捷的方式出现在搜索结果中,可以帮助你更好地应用seo。 不过,这里要记住一件事:SEO 策略只会为你的网站带来流量;在你的产品良好之前&a…...

【网络编程套接字(一)】
网络编程套接字(一)理解源IP地址和目的IP地址理解源MAC地址和目的MAC地址理解源端口号和目的端口号PORT VS PID认识TCP协议和UDP协议网络字节序socket编程接口socket常见APIsockaddr结构简单的UDP网络程序服务端创建套接字服务端绑定字符串IP VS 整数IP客…...
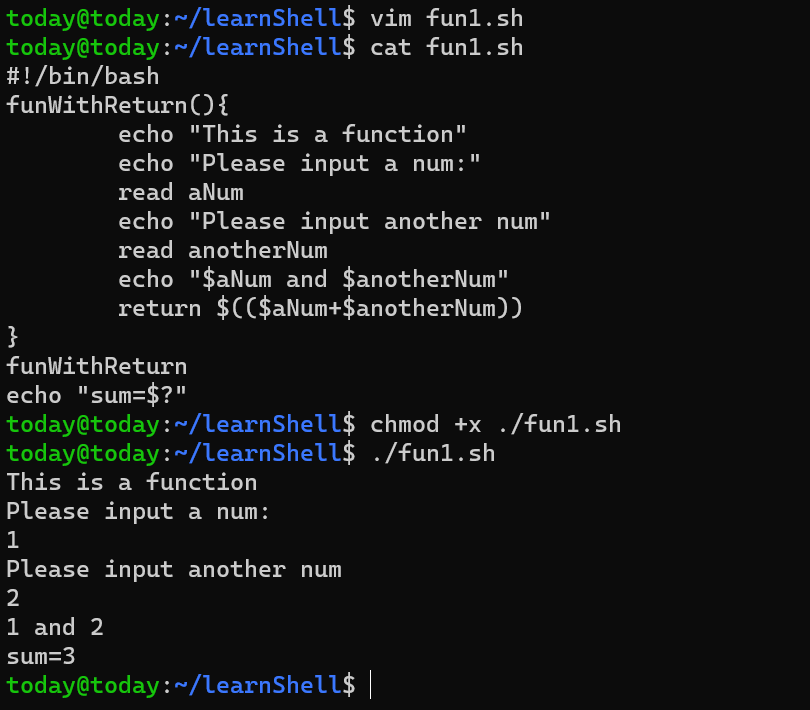
shell脚本入门
实习的时候第一个月的考核就是如何部署一个云资源,当时走的捷径(杠杠的搜索能力hhhh)找到了一个shell脚本一键部署,后来被leader问起来就如实说了,leader问有没有看懂shell脚本中的逻辑……(没有࿰…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...

免费PDF转图片工具
免费PDF转图片工具 一款简单易用的PDF转图片工具,可以将PDF文件快速转换为高质量PNG图片。无需安装复杂的软件,也不需要在线上传文件,保护您的隐私。 工具截图 主要特点 🚀 快速转换:本地转换,无需等待上…...

如何应对敏捷转型中的团队阻力
应对敏捷转型中的团队阻力需要明确沟通敏捷转型目的、提升团队参与感、提供充分的培训与支持、逐步推进敏捷实践、建立清晰的奖励和反馈机制。其中,明确沟通敏捷转型目的尤为关键,团队成员只有清晰理解转型背后的原因和利益,才能降低对变化的…...
