软件测试/测试开发丨利用ChatGPT自动生成架构图
点此获取更多相关资料
简介
架构图通过图形化的表达方式,用于呈现系统、软件的结构、组件、关系和交互方式。一个明确的架构图可以更好地辅助业务分析、技术架构分析的工作。架构图的设计是一个有难度的任务,设计者必须要对业务、相关技术栈都非常清晰才能设计出来符合需求的架构图。
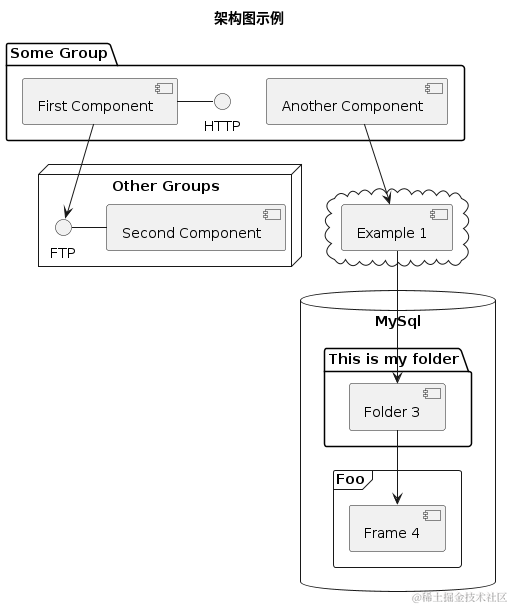
实践演练
1.有明确的业务的需求:业务需求必须要清晰不能模棱两可。如果业务需求不够清晰,那么在写提示词的之前,需要提前梳理一下业务需求,将它转换成ChatGPT可以理解的形式。
2.确定输出的格式:ChatGPT无法直接生成图形文件,但是可以通过Plantuml等各种文字转图片的工具间接生成。
- 提示词:现在我需要设计一个测试平台产品,这个产品需要包含测试用例的管理、用户管理、测试用例执行、执行记录管理,请根据以上信息帮我生成一张使用Plantuml绘制的类图。
以下是使用ChatGPT绘制出来的类图:
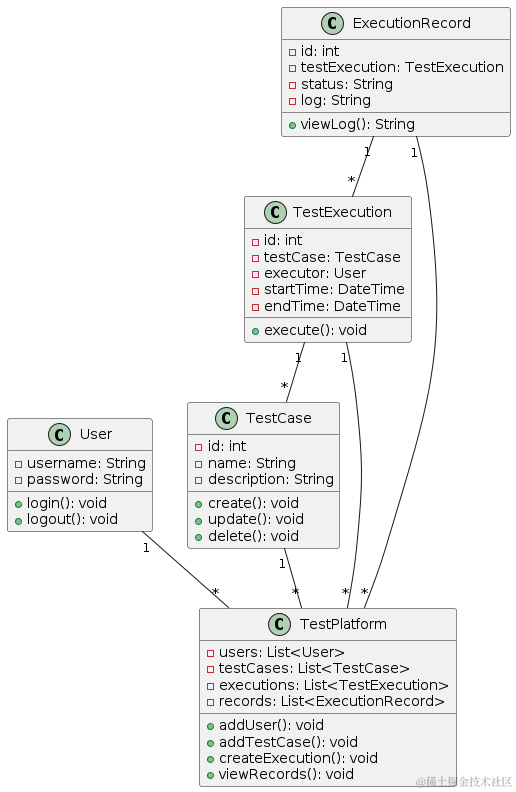
由上图可以看出 ChatGPT 将我们提到了的几个业务对象通过类的方式表示出来,甚至还罗列了可能包含的方法,如此一来便可以间接通过ChatGPT 以及 Plantuml 工具生成对应的架构图。
总结
在这次实践中,我们使用了ChatGPT 提示词的以下技巧:
1.写清楚需求:明确产品的需求,让生成的架构图更贴近需求。
2.系统的测试变化:如果中间步骤输出的信息不满足需求,可以通过提示词进行纠正与补充。
3.将复杂的任务拆分为更简单的子任务:直接生成图片或文件 ChatGPT 无法完成,但是可以通过曲线救国的方式间接生成架构图代码,然后再转换为图片。
相关文章:

软件测试/测试开发丨利用ChatGPT自动生成架构图
点此获取更多相关资料 简介 架构图通过图形化的表达方式,用于呈现系统、软件的结构、组件、关系和交互方式。一个明确的架构图可以更好地辅助业务分析、技术架构分析的工作。架构图的设计是一个有难度的任务,设计者必须要对业务、相关技术栈都非常清晰…...
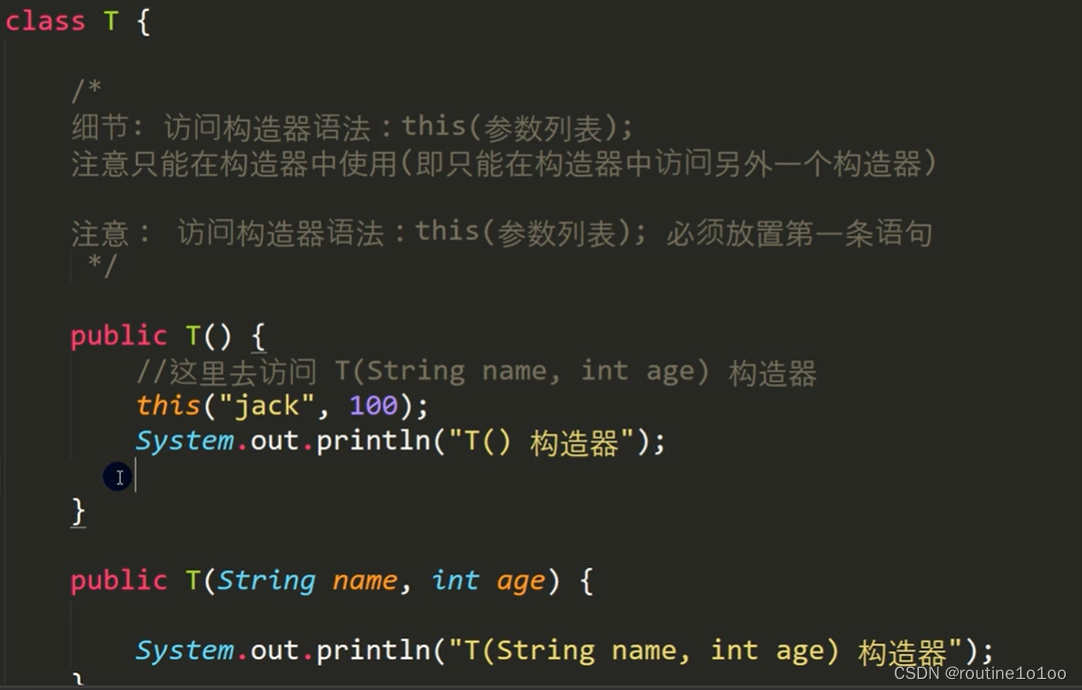
Java学习笔记(六)——面向对象编程(基础)
一、类与对象 (一)类与对象的概念 (二)对象内存布局 编辑 对象分配机制 编辑 (三)属性/成员变量 (四)创建对象与访问属性 二、成员方法 (一)方法…...
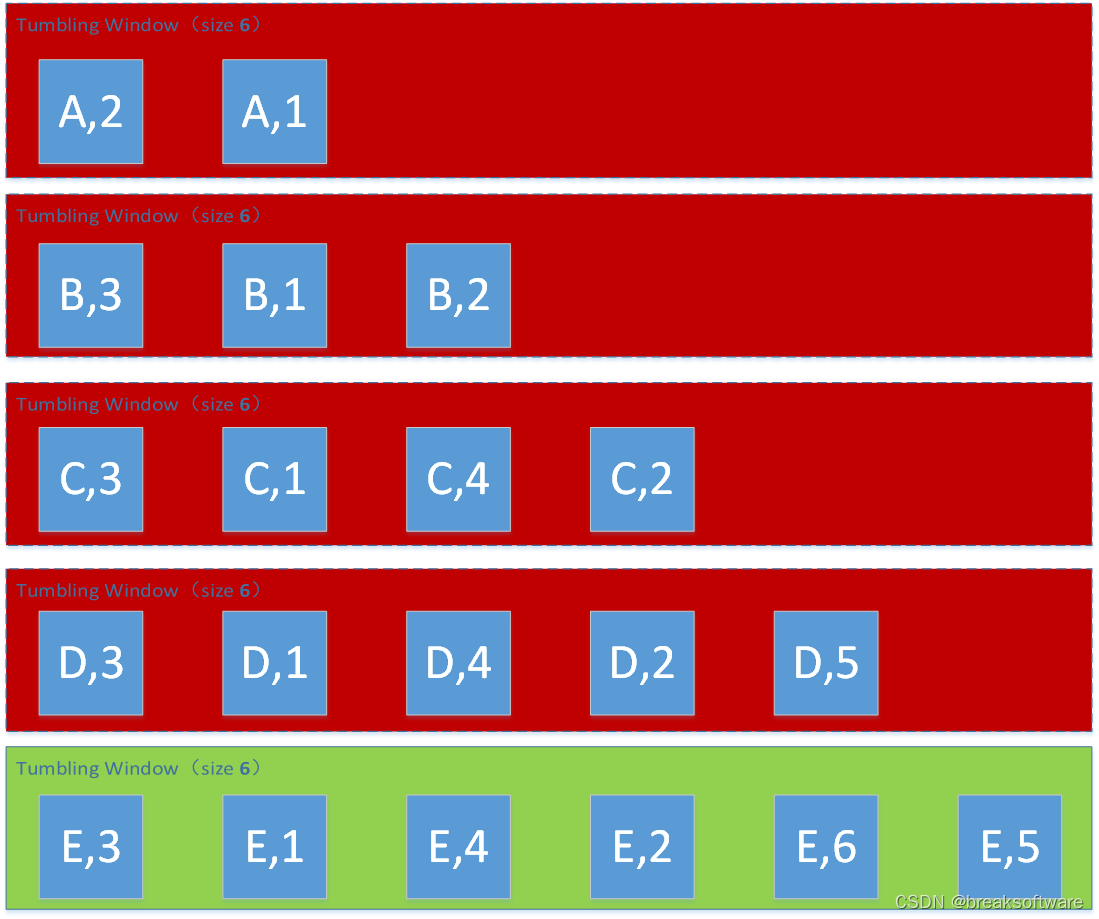
0基础学习PyFlink——个数滚动窗口(Tumbling Count Windows)
大纲 Tumbling Count WindowsmapreduceWindow Size为2Window Size为3Window Size为4Window Size为5Window Size为6 完整代码参考资料 之前的案例中,我们的Source都是确定内容的数据。而Flink是可以处理流式(Streaming)数据的,就是…...

车载终端构筑智慧工厂:无人配送车的高效物流体系
随着科技的不断进步和应用,智能化已经成为许多领域的关键词。在物流行业中,随着无人配送车的兴起和智慧工厂的崛起,车载终端正引领着无人配送车的科技变革之路。 文章同款:https://www.key-iot.com/iotlist/sv900.html 车载终端…...

插件_日期_lunar-calendar公历农历转换
现在存在某需求,需要将公历、农历日期进行相互转换,在此借助lunar-calendar插件完成。 下载 [1] 通过npm安装 npm install lunar-calendar[2]通过文件方式引入 <script type"text/javascript" src"lib/LunarCalendar.min.js">…...

【FreeRTOS】【STM32】08 FreeRTOS 消息队列
简单来说 消息队列是一种数据结构 任务操作队列的基本描述 1.如果队列未满或者允许覆盖入队,FreeRTOS会将任务需要发送的消息添加到队列尾。 2.如果队列满,任务会阻塞(等待)。 3.用户可以指定等待时间。 4.当其它任务从其等待的队列中读取入了数据(这时候队列未满…...
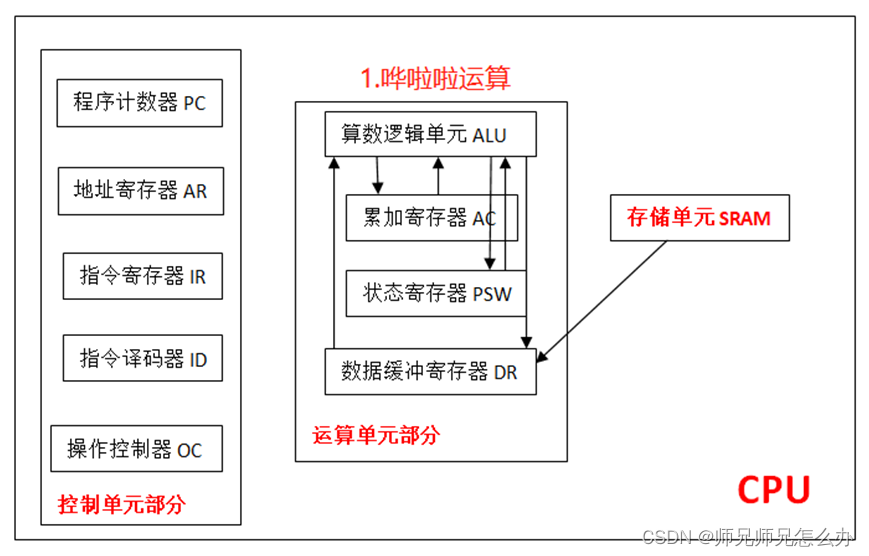
【计算机组成原理】CPU的工作原理
一.CPU的组成结构 CPU主要有运算器、控制器、寄存器和内部总线等组成,其大概的样子长这样: 看不懂没关系,我们将采用自顶而下的方法来讲解CPU的具体工作原理,我们首先来说一下什么叫寄存器,顾名思义,寄存器…...
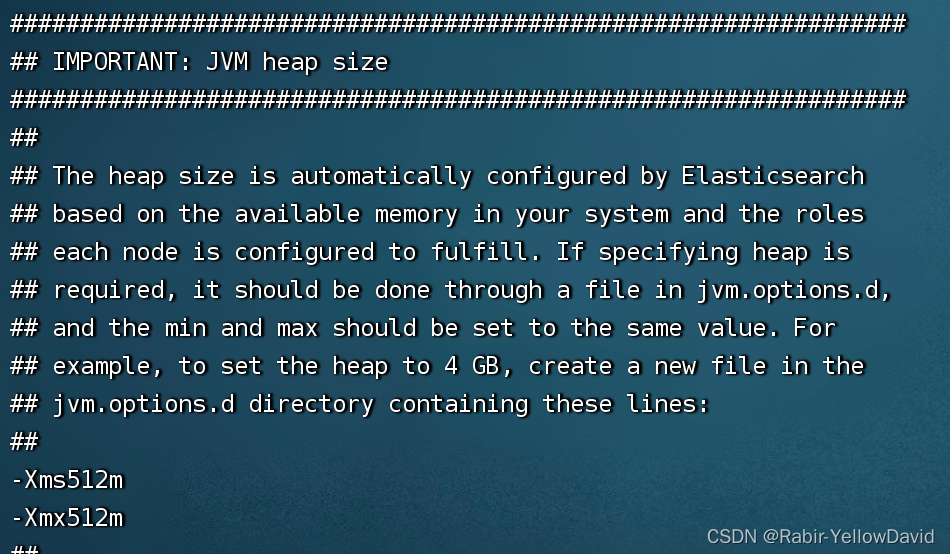
部署ELK
一、elasticsearch #拉取镜像 docker pull elasticsearch:7.12.1 #创建ELK docker网络 docker network create elk #启动ELK docker run -d --name es --net elk -P -e "discovery.typesingle-node" elasticsearch:7.12.1 #拷贝配置文件 docker cp es:/usr/share/el…...

纯前端实现图片验证码
前言 之前业务系统中验证码一直是由后端返回base64与一个验证码的字符串来实现的,想了下,前端其实可以直接canvas实现,减轻服务器压力。 实现 子组件,允许自定义图片尺寸(默认尺寸为100 * 40)与验证码刷新时间(默认时间为60秒)…...

#django基本常识01#
1、manage.py 所有子命令的入口,比如: python3 manage.py runserver 启动服务 python3 manage.py startapp 创建应用 python3 manage.py migrate 数据库迁移 直接执行python3 manage.py 可显示所有子命令...

什么是物流RPA?物流RPA解决什么问题?物流RPA实施难点在哪里?
RPA指的是机器人流程自动化,它是一套模拟人类在计算机、平板电脑、移动设备等界面执行任务的软件。通过RPA,可以自动完成重复性、繁琐的工作,提高工作效率和质量,降低人力成本。RPA适用于各种行业和场景,例如财务、人力…...

乐鑫工程部署过程记录
一、获取编译环境 1、下载sdk,ESP-IDF 这里有很多发布版本,当前我选择的是4.4.6,可以选择下载压缩包,也可以git直接clone 2、配置编译环境 我选择的是Linux Ubuntu下部署开发环境 查看入门指南 选择对应的芯片,我…...

to 后接ing形式的情况
look forward to seeing you. (期待着见到你) She admitted to making a mistake. (承认犯了个错误) He is accustomed to working long hours. (习惯于长时间工作)...

我做云原生的那几年
背景介绍 在2020年6月,我加入了一家拥有超过500人的企业。彼时,前端团队人数众多,有二三十名成员。在这样的大团队中,每个人都要寻找自己的独特之处和核心竞争力。否则,你可能会沉没于常规的增删改查工作中࿰…...

@EventListener注解使用说明
在Java的Spring框架中,EventListener注解用于监听和处理应用程序中的各种事件。通过使用EventListener注解,开发人员可以方便地实现事件驱动的编程模型,提高代码的灵活性和可维护性。本文将详细探讨EventListener注解的使用方法和作用&#x…...
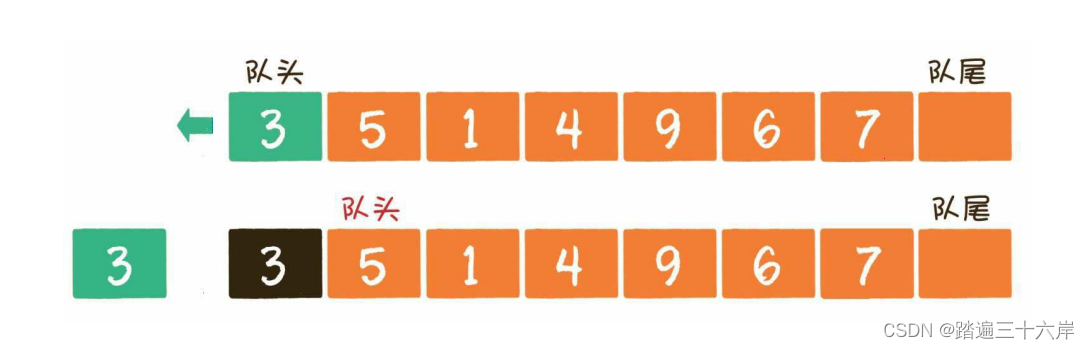
算法通关村第五关-白银挑战实现队列
大纲 队列基础队列的基本概念和基本特征实现队列队列的基本操作Java中的队列 队列基础 队列的基本概念和基本特征 队列的特点是节点的排队次序和出队次序按入队时间先后确定,即先入队者先出队,后入队者后出队,即我们常说的FIFO(first in fi…...

协力共创智能未来:乐鑫 ESP RainMaker 云方案线下研讨会圆满落幕
近日,乐鑫 ESP RainMaker 云方案线下研讨会(深圳)在亚马逊云科技与合作伙伴嘉宾的支持下成功举办,吸引了众多来自智能家电、照明电工、能源和宠物等行业的品牌客户、方案商和制造商。研讨会围绕如何基于乐鑫 ESP RainMaker 硬件连…...

读取谷歌地球的kml文件中的经纬度坐标
最近我在B站上传了如何获取研究边界的视频,下面分享一个可以读取kml中经纬度的matlab函数,如此一来就可以获取任意区域的经纬度坐标了。 1.谷歌地球中划分区域 2.matlab读取kml文件 function [sname,lon,lat] kml2xy(ip_kml) % ip_kml ocean_distubu…...
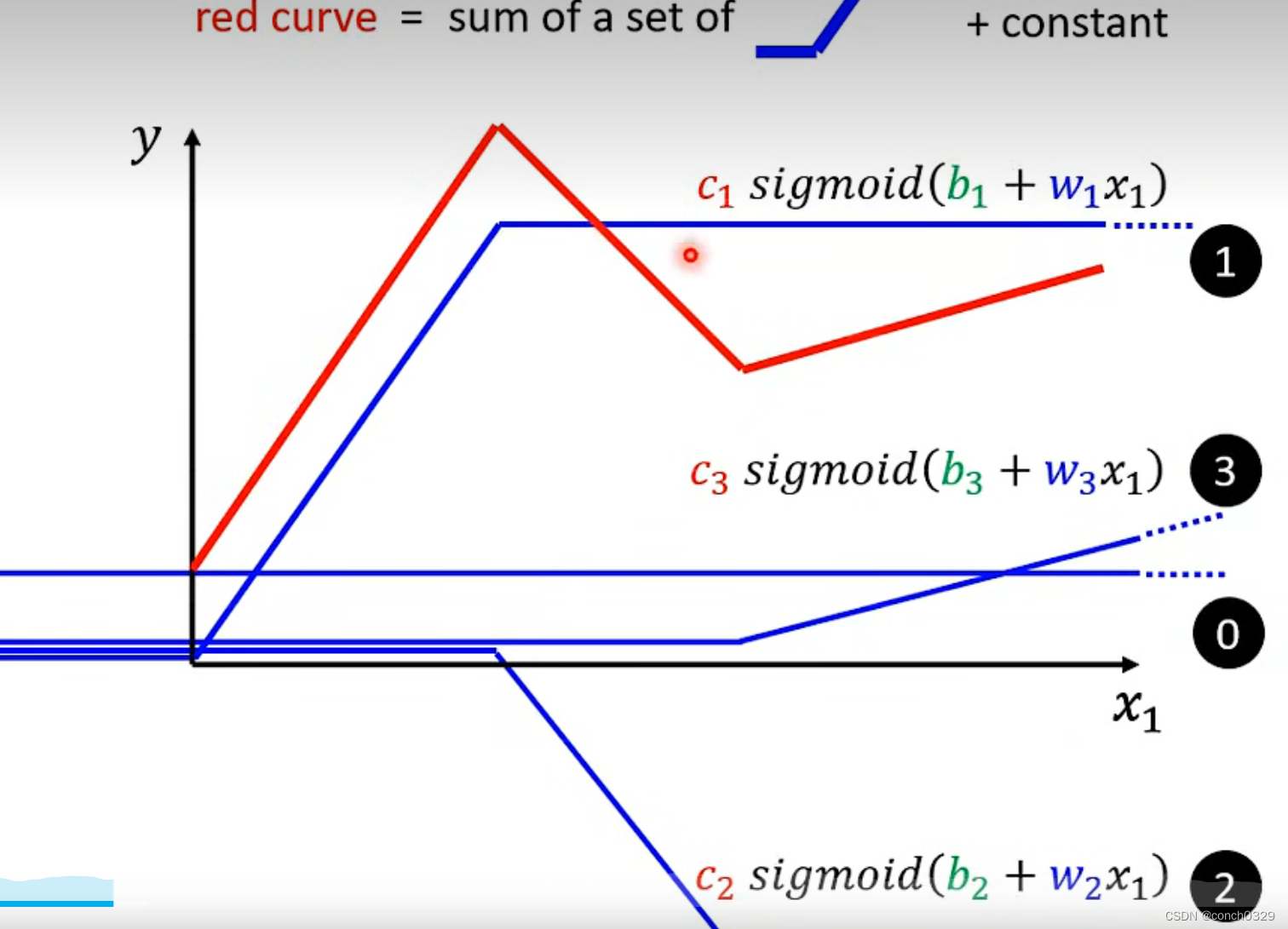
1深度学习李宏毅
目录 机器学习三件事:分类,预测和结构化生成 2、一般会有经常提到什么是标签label,label就是预测值,在机器学习领域的残差就是e和loss编辑3、一些计算loss的方法:编辑编辑 4、可以设置不同的b和w从而控制loss的…...
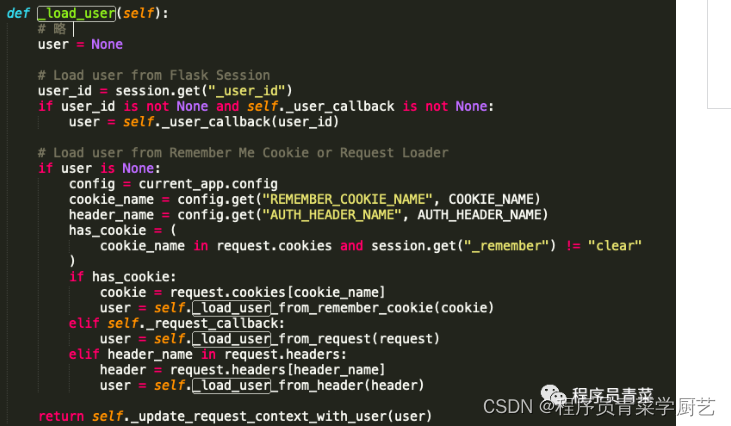
Flask_Login使用与源码解读
一、前言 用户登录后,验证状态需要记录在会话中,这样浏览不同页面时才能记住这个状态,Flask_Login是Flask的扩展,专门用于管理用户身份验证系统中的验证状态。 注:Flask是一个微框架,仅提供包含基本服务的…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...

BLEU评分:机器翻译质量评估的黄金标准
BLEU评分:机器翻译质量评估的黄金标准 1. 引言 在自然语言处理(NLP)领域,衡量一个机器翻译模型的性能至关重要。BLEU (Bilingual Evaluation Understudy) 作为一种自动化评估指标,自2002年由IBM的Kishore Papineni等人提出以来,…...
